考虑攻角约束的导弹制导控制一体化设计

吴 笛，王心明，何金刚，张金鹏，李世华*

(1. 东南大学 自动化学院，南京 210096； 2. 中国空空导弹研究院，河南 洛阳 471009)

0 引 言

在常规的设计过程中，导弹制导和控制系统通常是分离设计的，即传统的级联或双环制导和控制系统设计。这种分离的设计方法难以充分利用两个子系统之间的协同关系，也难以严格保证整个系统的稳定性[1]。同时，随着更高的性能需求和精度要求，特别是目标高机动的情况下，频谱分离的假设往往是不能被满足的[2-3]。

为了提高导弹的制导性能，文献[2-4]提出了制导控制一体化的设计框架。一体化设计是将制导与控制进行结合建模同时考虑，针对整个系统回路进行控制器设计，根据导弹与目标的相对运动状态直接生成舵角偏转指令。这一设计思路可以在一定程度上加快导弹的响应，大大减小脱靶量。近年来，基于一体化的设计思想，许多控制策略被应用来设计相应的制导律，如反步法设计、反馈线性化、滑模变结构控制方法、鲁棒控制等[5-11]。针对弹道导弹拦截器，文献[12]提出了一种基于反步法设计技术的自适应制导控制一体化控制方法。文献[13]在针对导弹一体化系统的控制律设计过程中采用了次优的θ-D控制方法。利用高阶滑模控制技术，文献[14]开发了一种用于拦截器的综合自动驾驶仪和制导算法。

在实际的应用中，导弹飞行时其攻角必须被严格的限定在一定范围内，才能保证其飞行的稳定性和良好的制导效果。一方面，导弹在飞行过程中必须限制导弹的正常过载，以防止结构损伤[15-17]。根据其气动特性，可以将导弹的过载约束转化为对攻角的约束[18]。另一方面，过大的攻角可能令导弹进入失速状态，导致其气动力的强非线性和强耦合变得非常严重，从而对导弹的稳定性和制导效果造成一定的影响[19-20]。基于此，各种方法被采用来实现导弹的攻角约束，如模型预测控制[21]、不变集概念[22]、参考调节器[23]、障碍李雅普诺夫函数法[24]等。模型预测的本质是将控制设计问题转化为优化问题，其难以处理建模的不确定性以及干扰带来的影响，同时对计算量的需求较大； 不变集是使从不变集开始的状态始终保持在这个集合之中，不变集本身的估计高度依赖于李雅普诺夫函数的选取，同时其对系统所有的初始状态都存在一定的约束限制； 参考调节器是通过对期望轨迹的规划来实现约束，但并不是直接作用于闭环系统状态，而是通过修改系统期望来实现对实际状态的约束，这还取决于系统的跟踪误差； 障碍李雅普诺夫函数法可以做到对输出的约束，但在运用反步法进行状态约束递推的时候，只能做到对虚拟控制器和状态之间的误差的约束。

本文针对二维制导控制一体化系统，考虑目标机动和导弹攻角约束的情况，提出了一种基于广义比例积分观测器(GPIO)带攻角受限的复合制导控制方法。首先，将导弹的制导与控制一体化系统作为一个整体的模型进行考虑。针对由目标机动和导弹参数摄动等带来的影响，将其作为集总扰动，设计了相应的广义比例积分观测器来获取对集总扰动的估计信息。针对制导与控制一体化这一整体的系统，利用分块反步法的设计思想，引入惩罚机制来对导弹的攻角进行约束，并在控制方案的设计过程中融入从GPIO所获得的集总扰动估计信息对系统中各通道的集总扰动进行精确补偿，实现在攻角受限的约束条件下的精确制导。通过严格的理论分析和数值仿真，验证了所提出的控制方案的有效性。创新点主要有以下三点：(1)控制器结构简洁，复杂度较低； (2)考虑目标机动和导弹参数摄动等带来的影响，以提高系统鲁棒性以及制导精度； (3)考虑到导弹攻角存在约束的情况，使得导弹攻角不会超出约束值。在控制器的设计过程中，既不对非约束的初始状态施加一定的限制(如不变集)，也不依赖于大量的计算量(如模型预测控制)，同时也不是对状态进行间接约束(如参考调节器、障碍李雅普诺夫函数法)。

1 问题描述

1.1 模型描述

在纵向二维平面xoy下，将导弹和目标都看作质点，导弹和目标之间的相对运动关系图，如图1所示。

图1 导弹-目标相对运动关系Fig.1 Missile-target relative motion relationship

图中，M和T分别为导弹和目标；q为视线角；r为弹目相对距离；am和at分别为导弹和目标的加速度；vm和vt分别为导弹和目标的速度；ηm和ηt分别为导弹航迹角和目标航迹角。基于此，可以建立导弹和目标相对运动的极坐标方程：

(1)

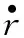
就轴对称战术导弹而言，弹体纵向加速度可以近似表示为

(2)

将式(1)～(2)整理重构，并采用近似cos(q-ηm)≈1，二维弹目相对运动模型可构造为

(3)

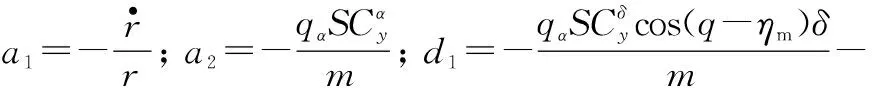
进一步，考虑如下导弹纵向弹目平面线性化姿态控制模型[25]：

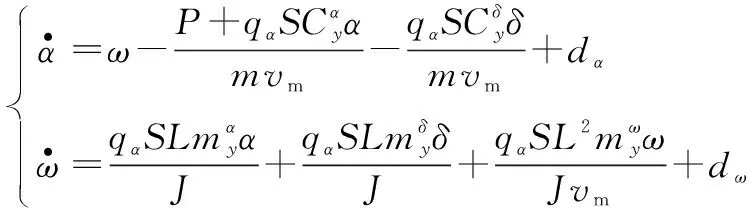
(4)

由此，式(4)可以简化表述为

(5)

(6)

即

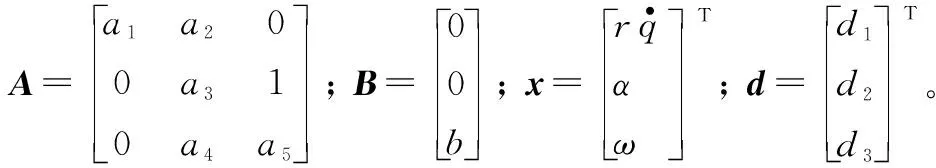
1.2 控制目标

为了实现控制目标，需进行以下假设：

本文的控制目标是实现攻角约束和对机动目标的末制导拦截。基于上述假设，可以将控制目标用如下的数学表达式进行描述：

(7)

2 主要结果

为了减轻外部干扰的影响，针对式(6)中存在的干扰进行广义比例积分观测器的设计，然后基于观测器对扰动的观测值进行前馈补偿，并在考虑攻角约束的情况下进行制导控制方法的设计。

2.1 广义比例积分观测器设计

针对式(6)中存在的干扰进行广义比例积分观测器的设计，然后基于观测器对扰动的观测值，并考虑攻角约束进行制导控制方法的设计。

考虑到受限的情况，且系统受到外部/内部干扰的影响(集总干扰)，故对扰动d1需有额外的限制条件。

定理1：针对式(6)，在满足假设3的前提下，构造如下的广义比例积分观测器：

(8)

式中：zk=[zk1,zk2,zk3]T∈3(k=0, 1, …,n)分别为x,d,…,d(n)的估计值;l0,l1,l2, …,ln为正常数; 扰动估计值将渐近收敛到集总扰动d，且对扰动各阶导数的估计值也会渐近收敛到真实值，即

证明：不难发现，式(8)可以拆解为三个观测器。不失一般性，这里仅对其中一个观测器给出证明过程。

定义误差变量：

e=[e0,e1, …,en]T

结合式(7)～(8)，可以构造如下观测误差方程：

(9)

2.2 基于观测器的攻角受限制导律设计

定理2：针对式(6)，结合式(8)，设计复合制导律：

(10)

(1) 闭环系统状态有界

(11)

将其沿式(6)求导可得

(12)

式中：k1>0为正增益常数；x3d为虚拟的输入信号。若将虚拟输入x3d设计为

(13)

则有

(14)

定义状态变量ξ=x3-x3d，构造Lyapunov函数：

(15)

将其对式(6)求导可得

(16)

若制导律u设计为

(17)

则有

(18)

综上所述，定义V=V1+V2，将式(14)和式(18)代入求导，且结合对于集总干扰d1的有界假设(假设4)，可以获得如下不等关系：

(19)

(20)

(21)

(3) 系统状态x1渐近稳定

3 仿真分析

为了验证本文所提出的制导控制方案的有效性，在Matlab/Simulink平台上进行了仿真。将式(10)和注释1中的普通复合制导律进行仿真比较。设系统初始条件为：r(0)=10 km，q(0)=30°，ηm(0)=45°，ηt(0)=120°。在末制导阶段，导弹和目标都具有恒定速度，分别为：vm=500 m/s，vt=250 m/s。控制约束(俯仰舵偏角)为|δ|≤30°。

针对三通道的干扰采用三组五阶GPIO(即n=4)进行观测估计。观测器增益选取为l0=25,l1=250,l2=1 250,l3=3 125,l4=3 125。

两种制导律的仿真结果如图2～6所示，包括导弹与目标的飞行轨迹、弹目相对距离r、攻角α、舵偏角δ和GPIO对干扰d1,d2,d3的观测曲线。

图2 导弹与目标的飞行轨迹Fig.2 Flight trajectories of missile and target

从图2可以看出，两种制导律具有相似的弹道。且弹道较为平滑； 图3弹目相对距离的曲线表明两种制导律均可击中目标。由于仿真对比的两种制导律均采用“前馈+反馈”的复合结构，且采用的增益参数是相同的，因此其对不确定性参数和扰动等都具有较强的鲁棒性(均能击中目标)。同时，本文所提出的带攻角约束的复合制导律可以保证攻角不超出约束限制，而大部分的情况，在两种制导律下，导弹的攻角都是离约束边界较远(如图4所示)，使得两者的控制输入，即俯仰舵偏角，是相似的(如图5所示)。因此，两种制导律下的结果是相似的，即具有相近的脱靶量和飞行时间。表1中给出了相应的脱靶量和飞行时间。从图4中可以明确看出，在整个制导过程中本文所提出的方法满足对攻角的约束，而去除惩罚机制之后的普通复合制导律存在攻角超出约束的情况。图6中给出了扰动估计曲线，由于两种方法的观测器的增益是相同的，因此两种方法是没有太大区别的。

图3 弹目相对距离曲线Fig.3 Curves of missile-target relative distances

图4 攻角曲线Fig.4 Curves of angle of attack

图5 俯仰舵偏角(控制输入)曲线Fig.5 Curves of pitch rudder angle (control input)

图6 扰动估计曲线Fig.6 Curves of disturbance estimation

表1 导弹脱靶量和飞行时间

4 结 论

将导弹的制导与控制系统结合起来进行一体化设计对于提高导弹整体性能具有重要的意义。本文主要针对二维的制导控制一体化系统(结合弹目相对距离模型和导弹的姿态模型)，考虑到其中干扰的影响，基于广义比例积分观测器对其进行观测，并在制导律中进行精确补偿。此外，在此基础上考虑导弹的攻角受限问题，在制导律中引入惩罚机制来对其进行有效约束。仿真结果表明本文所设计的制导律在保证较高制导精度的同时可以对导弹的攻角进行有效的约束。