动壁作用下流化气量对粉末供给特性的影响研究

任冠龙，孙海俊，徐义华，卢洪义，胡晓安

(南昌航空大学 飞行器工程学院 江西省微小航空发动机重点实验室，南昌 330063)

0 引 言

粉末发动机是以金属粉末为燃料、以粉末或气体为氧化剂的一类新型发动机。由于燃料为颗粒形式，可实现燃料供给和流量的灵活调节，从而让发动机具备多脉冲启停和推力可调控功能，正逐渐获得广泛的关注和研究。通过将燃料与氧化剂进行不同搭配，或者与传统发动机组合，目前国内外已发展出了多种粉末发动机类型，如粉末火箭发动机、粉末燃料冲压发动机、固体/粉末组合冲压发动机、粉末燃料水冲压发动机以及镁/二氧化碳粉末发动机等。

在各类粉末发动机研制过程中，粉末燃料输送是关键的共性技术。20世纪70年代，Frick等提出了利用气体作为载体进行粉末输送的方案。在此基础上，Meyer针对Al/Mg粉末-空气火箭发动机流化床式供给系统的活塞装置进行了改进，通过将流化进气道与活塞端面气孔相连，以使流化气均匀分布，同时防止粉末倒流。Foote等设计了一种容积式流化床(PDFB-Positive Displacement Fluidized Bed)粉末供给装置，该装置能使活塞运动更加平稳。Miller等进一步对粉末供给装置进行了改进，通过软管将气体输送至颗粒床，能更好地调节粉末储箱内压强。

国内对粉末燃料输送装置也开展了大量研究，文献[17-19]对粉末冲压发动机的燃料供应系统进行了实验和数值模拟研究，获得了电机驱动活塞方式下固气比、粒径、装置结构等参数对粉末输送性能和发动机点火性能的影响。文献[20-21]分别采用螺杆式和电机驱动活塞式粉末输送装置进行Mg/CO火箭发动机点火试验。为克服电机驱动和螺杆方式功率转调性能差、机械配合要求高等不足，文献[22-24]设计了一种更为简便高效的气压驱动活塞式粉末输送装置，并将该供给系统成功应用于Al/AP粉末火箭发动机多脉冲点火和推力调节、铝粉燃料冲压发动机以及Mg/CO火箭发动机点火试验等。

在粉末燃料气力输送装置中，粉末的流化输送特性是影响粉末流量调控以及输送装置性能的关键。Sun等对处于高压环境下粉末燃料的气力启动特性开展了研究，同时，又进一步对在高压环境下粉末流化特性开展了实验和数值计算研究。结果表明，高压条件下，粉末能够形成稳定的气固分界面，从而为粉末稳定输送提供了参考。霍东兴等对粉末燃料的沉降速度和最小流化速度进行了分析，得到了流化气压强、粒径等对最小流化速度的影响规律。Liang等对处于高压下密相气力输送流动特性进行了研究，并分析了流态化数和粒度对出料稳定性的影响。

可见，目前针对粉末储箱中复杂的稠密气固两相流动特性的研究还相对较少，尤其是活塞作用下的气体-颗粒-运动壁面相互作用机制更为鲜见。由于粉末储箱中稠密两相流动状态对颗粒流量调控有直接影响，所以很有必要对活塞作用下的气固两相流动特性开展研究。本文拟通过数值计算方法，对气体-颗粒-运动壁面相互作用特性开展研究，重点谈论流化气量对粉箱内稠密气固两相流动行为的影响，为粉末燃料供粉系统的优化设计提供参考。

1 几何模型与数值计算方法

1.1 粉末储箱构型

在稠密气固两相流计算中，流化床结构常被简化为二维/准二维构型以减少计算工作量，其计算结果表明二维/准二维构型亦能较好地体现三维流动状态，因此，本文将圆筒型粉末储箱结构简化为准二维构型。其中，粉末储箱为水平放置，储箱上下收敛段中心位置上各布置一气体入口，活塞简化为运动壁面，其运动方向为轴正向，同时在储箱出口设计一喉段，以控制最小出口截面面积。储箱结构参数如图1所示。

图1 粉末储箱构型Fig.1 Powder storage tank configuration

1.2 计算模型和方法

在稠密气固两相流计算中，由于颗粒数量庞大，采用离散元模型等进行计算会带来巨大的计算量，难以适用于工程计算。而双流体模型(Two Fluid Model, TFM)将颗粒相看作“拟流体”，将颗粒和流体均视为连续介质，二者在空间连续分布且互相渗透，其两相运动均可用Navier-Stokes方程描述，故计算量远低于离散元模型，该方法已广泛运用于化工领域流化床等方面。故本文采用双流体模型(TFM)来模拟粉末储箱内的两相流体动力学，气相湍流描述采用RNG-ε湍流模型，采用颗粒动力学模型(Kinetic Theory of Granular Flow, KTGF)用于对守恒方程中固相的封闭，压力-速度耦合采用PC-SIMPLE(Phase Coupled SIMPLE)算法，动量、湍流和体积分数方程中的对流项采用一阶迎风差分格式，气固相间作用描述采用Gidaspow曳力模型。颗粒与壁面之间为无滑移边界条件，采用瞬态模拟，时间步长设置为5×10s，每个时间步迭代20次。

计算采用空气进行流化，粉末燃料为铝颗粒，气体入口和两相出口分别为质量流量入口和压力出口边界条件，活塞运动通过UDF实现。由于不同流化气量下粉末储箱中会有相应的压力上升，故气体密度与压力之间满足气体状态方程，气体粘性则采用萨瑟兰定律描述。实际中，活塞运动速度主要取决于活塞两边受力之差，当驱动气压力和粉末量以及壁面摩擦阻力恒定时，流化气流量的增大会导致流化腔的压力升高，由此减小活塞两边受力差，活塞速度会减小，故活塞运动速度与流化气量之间存在耦合影响关系。在本文计算中，为研究单一变量，将不同工况下的活塞速度设置为固定值，仅通过空气流量变化实现工况的改变，计算工况如表1所示。进气流量按照粉末理论流量的百分比给定，而粉末理论流量则可通过活塞速度反算获得，进气流量与活塞速度存在对应关系，其对粉末流化具有耦合影响关系:

表1 计算工况

(1)

颗粒属性及操作条件如表2所示，表中操作压力是指粉未储箱内的压强环境。

表2 操作条件参数

2 网格无关性验证

使用ICEM软件生成结构化六面体网格，网格无关性验证采用的网格数分别为3万、10万、20万及40万。不同网格数时中心截面(=0.003 m)=0.090 m处颗粒轴向速度分布，如图2所示。由图可见，20万网格和40万网格的计算结果整体差异很小，在=0.055 m附近，10万网格、20万网格和40万网格的计算结果差异较大。为减小计算量，本文采用网格数为20万左右网格进行计算。

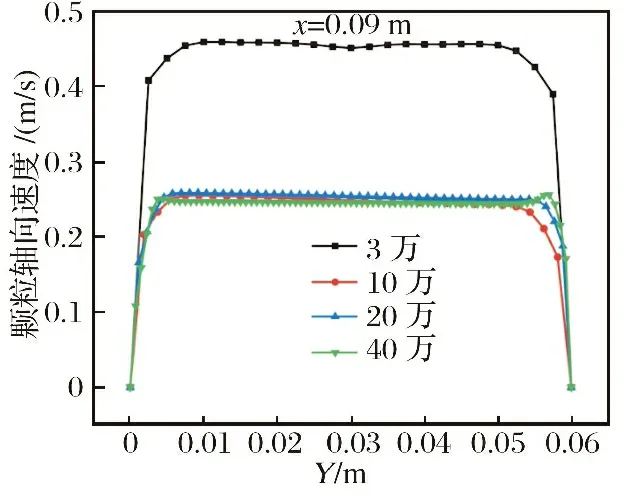
图2 网格无关性验证Fig.2 Grid independence verification

3 计算结果与分析

3.1 计算模型验证

为了验证所选计算模型的正确性，需要将图1所示几何构型的计算结果与实验结果进行对比分析，如图3所示。在粉末流化过程中，压降率是研究颗粒特性的重要参数。压降率是指储箱启动前的初始压力与工作一段时间后的稳定压力之差，是供粉系统稳定工作特性的表征参数之一。其计算公式为

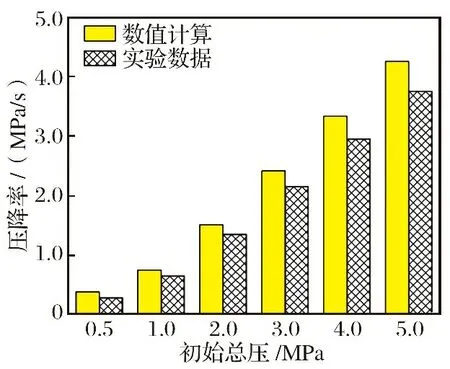
图3 计算模型验证Fig.3 Calculation model verification

(2)

式中：为初始总压；为终止压强； Δ为时间间隔。

由图3可见，数值计算结果与实验值基本吻合，且数值计算数据与实验数据最大误差在13%以内，计算精度满足要求，表明所选择的计算模型和方法能够较好地用于质量流量对粉末流化特性的影响研究。

3.2 粉末流化过程

粉末储箱向中心截面不同时刻粉末体积分数分布，如图4所示。由图可见，在=0.005 s时刻，不同工况下的颗粒均呈现上下对称分布。由于此时粉末储箱处于刚启动阶段，随着流化气量的增大，储箱收敛段处气相作用范围也在不断增大，颗粒在流化气和运动壁面的共同作用下开始运动，不断从粉末储箱输出。在粉末储箱出口，工况1几乎没有颗粒流出，工况2和工况3有少量颗粒流出，工况4和工况5则有较多颗粒流出。

在=0.030 s时刻，气相作用面积较图4有较大的增加，但整体而言仍基本处于上下对称分布态势。随着气体流量的增大，气相作用范围增加幅度越来越明显，由工况1中轴向范围[0.150 m，0.170 m]扩大到工况5中轴向范围[0.120 m，0.177 m]，储箱收敛段内的颗粒几乎被掏空，该现象在工况4和工况5中最为明显。这在于气体流量的增加会相应增大气体动能，从而增强气体对颗粒的卷吸与运输能力，进而将更多的颗粒输送出去。值得注意的是，此时在上下气动力以及颗粒自身重力共同作用下，被卷吸起的颗粒主要分布在中心轴线上，即在中心轴线上形成了明显的气固两相流道。

图4 颗粒体积分数分布云图Fig.4 Particle volume fraction distribution

在=0.055 s时刻，颗粒上下分布，对称分布现象消失，呈现出上部气相范围大于下部的态势，但下部气固界面相比上部要稳定。这是由于储箱内颗粒整体受力主要有活塞向前推动力、自身重力以及气相作用力，在储箱收敛段上、下部分，其受力情况出现不统一，故而呈现出不同的粉末分布态势。在收敛段下部区域，颗粒在活塞以及重力作用下趋向于沉降，而此时流化气对颗粒的作用则是扬起，当颗粒所受活塞推动力与重力的合力，与颗粒所受气相作用力相平衡时，就能形成相对稳定的气固分界型面； 而在收敛段上部区域，颗粒的主要受力很难实现平衡，且此时气相作用力占主导地位，导致粉末分布相比下部更难形成稳定型面。相比前时刻，该时刻锥形收敛段内重新充满了颗粒，但颗粒体积分数相对较低，原因是颗粒在流化气卷吸作用下不断被输送出粉末储箱，而活塞则在不断将颗粒沿轴向向前推进，流化气卷吸带出的颗粒所留下的空隙由活塞推动的颗粒填补，二者形成协同作用。而当活塞向前推送的粉末量小于被气力输出粉末量时，则会造成填补处颗粒体积分数较低的现象。同时由图可见，粉末低浓度区域面积随气体流量的增大而增大，主要在于所有工况下活塞运动速度一致，即活塞向前推送的粉末量一致，而流化气较小时，其卷吸输出粉末量也相对较小，活塞推送粉末量与输出粉末量容易形成动态平衡，故而会形成如工况1中所示气固分界面较清晰的现象。

在=0.185 s时刻，各工况下粉末低浓度区域相比上一时刻有较大缩减，随之是空腔(气相区)面积增大，且空腔主要分布在粉末储箱锥形收敛段的上部。这是由于颗粒重力的影响主要施加在下部进气上，导致下部气体流动空间受限，而上部气体流动受阻相对要小得多，通过不断卷吸输出粉末，气体在储箱顶部做延伸运动。工况4和工况5中流态要更为复杂，其低浓度粉末区域相对较大，主要还是由于大流化气量下输出的粉末量也相对较多，活塞推送粉末量难以足额填补。另一方面，较大的气体流量拥有较大的动能，其对粉末的扰动也相对更大，故而流态更为复杂。

在=0.335 s时刻，随着流化气不断将粉末卷吸输出，而活塞向前推送的粉末量恒定，导致出现了粉末储箱上方粉末被逐渐掏空的现象。同时随着流化气量的增大，粉末储箱上方气固分界面处的低浓度粉末区域也随之增大，进一步表明流化气量越大，其卷吸输出的粉末量越多。此时刻不同工况下，在=0.148 m附近，颗粒床出现突起现象，且随着流化气量增大越发明显，这主要是由于向内卷吸气流形成的回流旋涡与上部进气相互冲击，导致粉末被卷吸扬起，而流化气量越大，其相互作用动量越大，故效果越明显。在=0.500 s时刻，不同工况下粉末储箱上方粉末都基本被卷吸输出，出现明显的气固上下分界现象，表明活塞推送粉末量不足以平衡各工况下粉末的输出量。

在=0.950 s，=1.220 s，=1.875 s和=2.305 s时刻，流动状态趋于稳定，气固分界型面呈水平分布，表明此时活塞向前推送粉末量与输出粉末量维持平衡，由此可形成相对稳定的粉末型面。但随流化气量增大，粉末型面处低浓度区域增大，同时整体粉末体积分数随之减小。由此表明虽然不同流化气量都能形成相似的粉末型面，但较大的流化气量由于卷吸输出的粉末量多，表现在整体粉末体积分数的下降上。

3.3 流化过程参数分析

3.3.1 颗粒平均体积分数

颗粒平均体积分数能够较好地体现流化过程中颗粒的运动范围，图5为中心截面(=0.003 m)=0.150 m处，不同流化时刻处颗粒平均体积分数分布。从图中能够看出除0.030 s时刻处外，其余时段曲线分布趋势相似。

图5 不同时刻处中心截面X=0.150 m处颗粒平均体积分数沿Y向分布Fig.5 Average volume fraction of particles at the central section X=0.150 m distributed along Y direction in different times

在流化时刻0.030 s处，工况1的颗粒平均体积分数沿轴方向呈直线分布，其余工况则呈“W”型分布。表明在此时段内，工况1气体对粉末的影响最小。而工况2～5随着流化气量的增大，气体对粉末的作用增强，导致平均体积分数曲线波动明显，呈现“W”型分布，即体积分数曲线在两端和中间(=0.03 m)呈现较大分布状态。其原因在于此时段内，气体对粉末的作用还主要集中在收敛段内，故曲线两段粉末浓度分布相当，而颗粒在自身重力以及上下流化气的共同作用下，被卷吸起处于悬浮状态，并在=0.03 m附近聚集，然后被输出，故此处颗粒浓度增加。工况1由于流化气量低，此时还未形成低浓度两相区，故平均体积分数曲线在向保持一致。

在流化时刻0.950 s、1.875 s以及2.900 s处，颗粒平均体积分数曲线趋势大同小异，在轴[0 m，0.03 m]范围内，五个工况的曲线下降范围在[0.50，0.62]之间，且下降趋势较为平缓，但工况5的曲线陡峭且始终处于最下方。在轴[0.03 m，0.05 m]范围内，五个工况的曲线下降范围在[0.02，0.50]之间，但下降趋势比在轴[0 m，0.03 m]范围内时更快，且在同一时刻，不同工况之间的颗粒平均体积分数差距逐渐减小。在=0.035 m附近，五个工况存在一个交点，在轴[0.030 m，0.035 m]范围内，颗粒平均体积分数曲线从上至下依次排序为工况1、工况2、工况3、工况4、工况5，原因是运动壁面匀速运动下，流化气量越大，其卷吸携带出的颗粒较多，粉末储箱内堆积的颗粒较少，导致颗粒床层高度降低，同时表明在上述时间段内，不同工况都形成了相对稳定的气固分界型面。在工况5中，图中显示的曲线代表的是流化气卷吸起的颗粒，相比于堆积的颗粒床颗粒平均体积分数较小； 在轴[0.035 m，0.050 m]范围内，颗粒平均体积分数曲线从上至下依次排序为工况5、工况4、工况3、工况2、工况1 ，原因是该范围处于粉末储箱的上方，此处没有颗粒堆积，图中显示的曲线代表的是流化气卷吸起的颗粒，流化气量越大，卷吸起的颗粒就越多。在轴[0.05 m，0.06 m]范围内，五个工况的曲线下降范围在(0，0.02)之间，但工况5的曲线处于最上方，这在于工况5流化气量最大，其充足的动能可将颗粒更高地扬起。

3.3.2 粉末流量特性

在整个流化过程中，各个工况瞬时粉末质量流量与理论流量对比，如图6所示。为更直观获得流化过程稳定后的质量流量与理论质量流量的关系，对1.2～2.9 s时段内瞬态流量进行平均化处理。由图可见，在启动阶段(0～1.2 s)，不同工况下均出现了较大的流量波动，表明此时段内有大量的粉末被输送喷出。而之后流量曲线仍有波动，但整体相对平稳，表明此时输送处于动态平衡状态。在0～1.2 s时段，随流化气量增加，流量峰值随之增加，同时伴随更为明显的流量振荡，表明气量越大，两相间相互作用更为剧烈。值得注意的是，不同工况在1 s左右都有个流量小峰值，这个峰值的产生在于此前在=0.15 m处有颗粒被卷吸扬起现象，并最终输出造成又一流量峰。在输送稳定阶段(1.2～2.9 s)，流量曲线仍存在振荡，但振幅降低明显，整体区域平稳，工况1～5平均流量分别为0.015 5 kg/s, 0.015 4 kg/s, 0.016 6 kg/s, 0.016 8 kg/s, 0.017 7 kg/s，基本呈现出随着流化气量增加而增加的趋势。各工况下平均流量与理论流量间存在较大差距，主要原因是在0～1.2 s时段，大量颗粒输送喷出，导致储箱内粉层高度下降一半，由此在稳定阶段输送出的流量较理论流量要小得多。

图6 不同工况质量流量分布Fig.6 Mass flow rate distribution under different cases

粉末流量随时间振荡现象是实际中就存在的，在先前的开窗拍摄实验中，不同流化压强条件下，粉末型面在启动阶段会有波动，由此造成出口流量波动。随着流化压强的增大，其粉末波动幅度较小，可形成相对稳定的气固分界型面，即粉末波动幅值较小。另一方面，之前对粉末流量的测量实验研究表明，不同的测量方法下，粉末流量也会随时间振荡。数值模拟的流化过程以及粉末流量特性与实验结果相似，表明粉末流量振荡是实际存在的。通过分析粉末流量特性可知，进气流化气量对出口流量影响较大，由于较小流化气量能够降低曲线波动程度，所以可通过降低进气流量的方式，来改善粉末的输出稳定性，但在实际应用中需要根据设计的粉末流量来确定流化气量，即不同的粉末流量所对应的最佳流化气量不相同，可根据实验建立粉末流量与流化气量之间的最佳匹配关系，由此确定流化气量的选择。

3.3.3 粉末储箱内压强和运动壁面受力特性

不同工况粉末储箱内瞬时压强和运动壁面瞬时受力分布，如图7所示。由图可见，各个工况粉末储箱内压强曲线和运动壁面受力曲线分布趋势大同小异，整体分布趋势类似于流量分布曲线，即各工况下在启动阶段呈现高压分布，之后压力降低，虽仍有振荡，但整体而言较为平稳。

图7 不同工况粉末储箱内压强和运动壁面受力分布Fig.7 Distribution of pressure in the powder storage tank and force on moving wall under different cases

在粉末储箱处于启动阶段，曲线出现峰值，且曲线出现峰值的时间随着流化气量的增大而提前，峰值随着流化气量的增大而增大，符合压力器件启动效应。在时间段0.05～0.8 s内，压力上升并在此时间段一直处于较高位，表明此时段一部分气体用于将粉末输出，另一部分则在储箱内与粉末相互作用。之后时间段，压力曲线降低并伴随小幅平稳振荡，表明此时段流化趋于稳定，流化进气与出气流量维持动态平衡。另一方面，随流化进气量增大，储箱内压力随之增大。

运动壁面的受力是粉末与气体相互作用的结果。运动壁面受力趋势与压强分布趋势一致，虽然运动壁面受力来源于粉末阻力和气体压力，但相对而言，压力对运动壁面受力的影响要远大于粉末，尤其是在平稳段，在粉末储箱上部，运动壁面受气压作用，在粉末储箱下部，运动壁面受颗粒与气压共同作用，整体而言气压影响占据绝对优势。可见，在整个流化过程中，运动壁面(活塞)所受瞬时平均压力变化剧烈，这在实际应用中会引起活塞综合受力不均，容易引起活塞速度的突变，同时由于活塞主要受气压影响，故要在工程中维持活塞速度稳定，前提是要保证整个流化过程中流化压力的稳定，这也是活塞驱动式粉末供给系统设计的关键所在。

4 结 论

本文针对气压驱动活塞式粉末燃料供给系统，建立了考虑运动壁面作用下的稠密气固两相计算模型，并详细分析了流化气量对粉末流化过程和输送特性的影响，主要获得以下结论：

(1) 粉末流化状态受气体、活塞运动以及颗粒自重等因素共同影响，当活塞向前推送粉量与粉末被卷吸输出量呈动态平衡时，不同工况下均能形成相对稳定的颗粒床层型面，但颗粒床层浓度随流化气量的增大而变小。

(2) 在启动阶段，气体对粉末有较大的卷吸输出量，其输出量远大于粉末理论流量且随流化气量的增大而增大。在稳定输送阶段，不同流化气量下的粉末平均流量都小于粉末理论流量，粉末平均流量随流化气量增大而增大。

(3) 不同工况在启动阶段时的压力都明显高于输送稳定阶段，较大的流化气量会形成相对较高的储箱压力； 活塞瞬时受力与瞬时压力分布趋势一致，气压是对活塞受力影响的主要因素，在工程应用中要维持相对稳定的活塞速度，首要前提是保证储箱气压相对稳定。