电感耦合等离子体放电特性的三维仿真研究

郭 旭，李颖晖，邱辰霖，常怡鹏，王瑶东

(1. 空军工程大学，西安 710038； 2. 中国人民解放军93131部队，北京 100038)

0 引 言

等离子体隐身开辟了隐身技术的新领域，相较于传统隐身技术，具有吸波频带宽、易于控制且可以长时间使用等优点[1-2]。在飞行器表面覆盖大面积的电感耦合等离子体具有衰减雷达回波的效果。电感耦合等离子体放电是指射频电源通过阻抗匹配网络的调制后驱动线圈，产生交变的射频磁场，在充满稀有气体的密闭腔体中感应产生射频电场，电场加速电子，进而产生等离子体，能量通过线圈产生的感应磁场与等离子体耦合。ICP装置结构相对简单，放电参数易于调节，可在较低的功率和气压下得到高密度的等离子体[3-6]。对等离子体放电最早的探索始于Hittorf[7]研究的一种无电极环形放电装置，后来，盘香形放电线圈凭借其能产生高密度的等离子体而得到应用与发展，在材料处理等领域广受关注。

在隐身技术领域，利用ICP来衰减目标的电磁波散射，降低其雷达特征，使雷达发现目标的距离更小。而分析ICP的电磁散射特性的前提，是要得到等离子体频率ωp和碰撞频率νm这两个关键参数[8]。等离子体频率可以表示为

(1)

式中：ne为电子在腔体中的密度；e为电子自身携带的电量；me为电子质量；ε0为真空电容率(近似值为ε0=8.854×10-12F/m)。

而碰撞频率可由经验公式得到

(2)

式中：P为腔体内气体压强，单位为Pa；Te为电子温度，单位为eV。

由式(1)可知，对等离子体电子密度等参数的研究，是进行ICP电磁散射特性分析的前提。对此，国内外学者针对等离子体放电和等离子参数诊断做了大量工作。针对放电问题，Hopwood等利用朗缪尔探针来研究ICP中的电子密度[9]。Tyshetskiy等通过测量ICP中的电子密度以及线圈中的电流，证明了ICP中存在无碰撞电子加热[10]。Ventzek等通过改变天线结构、匝数及放置位置，研究外界因素对ICP放电特性的影响[11]。国内陈俊霖等针对雷达罩隐身设计了一种石英夹层ICP天线罩模型，研究了与电磁散射特性相关的ICP电子密度空间分布[4]。然而这些研究目前是利用二维模型进行计算，即使有三维结果，也是在二维模型的基础上进行旋转或拉伸产生，并不能完全反映实际放电过程中等离子体参数的分布。

针对上述工作中的不足，本文主要利用COMSOL_Multiphysics仿真平台建立三维仿真模型，对闭式石英腔构型的ICP在不同条件下的放电参数进行研究，在很大程度上提高了数值仿真的精确度和真实性，解决了非对称或不规则模型的构建问题。研究结果对于探究等离子体参数分布对电磁散射特性的规律具有指导意义。

1 仿真模型

1.1 ICP的物理构型

按照线圈的几何形状和位置分布，ICP源的结构可以分为两类，一种是将射频驱动线圈缠绕在柱状密闭反应腔室的侧面，称为柱状线圈型； 另一种则是将射频驱动线圈沿腔体轴心向外径方向盘成蚊香状，放在反应腔室的顶部，称为平面线圈型[7]。

本文研究的透波腔感应耦合等离子体几何构型的示意图如图1所示，鉴于选用的是三维轴对称模型，为标示方便，这里只给出了模型的剖面图。

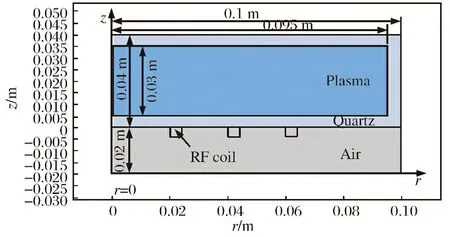
图1 ICP在COMSOL中的几何构型Fig.1 Geometry of ICP in COMSOL

充斥气体的腔体外形是简单的长方体，底面边长为0.19 m，腔体厚度0.03 m； 外面包裹透波性较好的石英夹层，夹层的厚度为0.005 m； 铜制的射频线圈安装在腔体底部的石英窗口下，其位置分布根据需要进行设定。

1.2 ICP的流体模型

本文研究的ICP属于低温等离子体，可以用扩散漂移方程来表示电子和电子能量的输运[12]。

电子连续性方程可以表示为

(3)

电子能量密度的连续性方程可以表示为

(4)

表1 模型涉及的化学反应

表1中的F(n) 为一个依赖于电子能量分布函数的变量，其具体表达式如下：

(5)

式中：γ=(2e/me)1/2为一个由电子电量和电子质量组成的常数；ε为电子自身携带的能量；σk(ε)为在粒子碰撞过程中的截面；f(ε)为电子能量分布函数。

对于重粒子的质量守恒，使用混合平均的方法分析计算，任取一种粒子k需要满足：

(6)

式中：jk为粒子的扩散流；Rk为粒子k产生的速率；u为重粒子平流过程中的流速；ρ为混合重粒子的密度；ωk为粒子的质量分数。

对于腔体中的矢量磁势分布，采用频域下的安培定律进行求解：

(7)

式中：σ为腔体内物质的电导率;εr为相对介电常数；A为腔体内的磁势；μ0为真空条件下的磁导率；μr为相对磁导率；Je为流经射频线圈的电流。

该磁场在腔体内产生感应的电场可以由电磁感应定律求得, 即

E=-jωA

(8)

由此可得等离子体输入功率为

Pind=(1/2)·real(E·J)

(9)

式中：J=εEe为腔体内产生的感应电流。

利用仿真平台COMSOL中的ICP模块对该流体模型进行有限元计算，ICP装置的网格剖分示意图如图2所示。

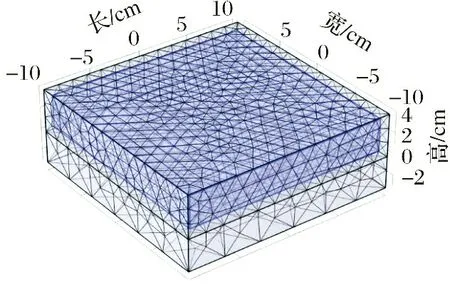
图2 ICP装置的网格剖分示意图Fig.2 Schematic diagram of grid division of ICP device

2 初始条件和边界条件

为减小计算量，以纯氩气为放电气体，放电过程中电子密度的初值设置为ne0=1×1016m-3，平均电子能初值为ε0=4 eV，同时将环境温度设定为300 K，气压根据仿真需要进行设定。具体的数值模拟参数如表2所示。

表2 ICP放电的数值模拟参数

本文建立的边界条件考虑了：(1)由于电子进出壁面时的通量差值而产生的丢失； (2)二次电子发射以及热电子发射导致电子的增加，其分别是由正离子撞击壁面以及激发态粒子与壁面作用产生的。边界反应选取如表3所示。

表3 边界反应

3 仿真结果及分析

3.1 等离子体参数随时间的分布规律

3.1.1 电子密度的分布规律

当腔体内的气压为5 Pa，线圈功率100 W时，不同时刻电子密度在腔体内的空间分布如图3所示。为了观察方便，选取三维仿真模型的横截面进行分析。在t=10-8s时，射频线圈开始在腔体内感应出电场并电离氩气，此时电子密度为ne=1.01×1016m-3，比模型设定的初始值略大。t=10-7s时，电子密度增加并且空间分布主要集中在放电线圈附近，此时线圈在等离子体趋肤层内感应出较强的加热电场，功率通过加热电场耦合给氩气，使其电离产生电子。

图3 电子密度的空间分布随时间的变化Fig.3 Variation of spatial distribution of electron density with time

从t=10-6s到t=10-3s，电子密度的峰值区由趋肤层附近逐渐向腔体中心区域移动。在低气压条件下，粒子碰撞的平均自由程与腔体的几何尺寸在数量级上相当，电势分布的峰值区跟随电子的扩散迁移。由于放电区域的双极性电势是气体电离率的主要影响因素，向中心区域移动的电势使得该区域气体的电离率逐渐大于周围区域。此外，低能电子受电场力的作用会在腔体的中心区域积累，占比较多的低能电子会导致峰值区电势减弱。在t=10-3s时达到动态平衡，峰值区域电子密度的最大值为ne=3.97×1017m-3。

3.1.2 电子温度的分布规律

电子温度Te直接影响化学反应的速率和能量传递过程，是表征电子能量的参数，对碰撞频率分布有重要影响。气压5 Pa，功率100 W时, 电子温度在不同时刻的分布如图4所示。从仿真结果可以看出，放电伊始，线圈附近的电子温度数值较高且分布相对集中，主要是因为此时趋肤层内的电子获得了耦合功率，电子能量升高，运动频率增加。

图4 不同时刻电子温度的分布Fig.4 Distribution of electron temperature at different times

从t=10-8s到t=10-5s，携带能量的电子在腔体内通过碰撞过程向中心区域扩散，电子温度升高的同时分布趋于均匀。从t=10-5s到t=10-3s，电子通过加热场获取能量，同时通过非弹性碰撞电离气体损失能量。当二者达到平衡时，电子温度的变化趋于稳定。电子温度峰值在整个放电过程中一直处于线圈附近而没有向中心区域移动，这主要有两方面的原因：一是在靠近线圈的加热场内，电子可以通过功率耦合获得更多能量； 二是电子在向中心区域扩散的过程中，通过碰撞作用会不断损失能量。因此，中心区域的电子温度低于线圈附近。

3.2 放电条件变化对等离子体参数分布的影响

建立流体模型，主要在不同线圈功率、气体压强下对等离子体参数分布进行研究。功率Ps选取的范围为100～300 W，气压P选取的范围为5～200 Pa。

3.2.1 线圈功率对等离子体参数分布的影响

在腔体结构不变、气压固定为5 Pa的条件下，将线圈功率分别设置为100 W，200 W和300 W，研究氩气环境下的等离子体放电特性。为了方便比较仿真结果，选取了三维模型的剖面图进行分析，如图5所示。

图5 不同放电功率下电子密度的空间分布Fig.5 Spatial distribution of electron density under different discharge power

图5给出了气压固定为5 Pa时不同放电功率条件下电子密度的空间分布。从仿真结果可以看出，电子密度在腔体空间内的分布出现梯度变化，靠近中心区域的电子密度最高，靠近边界处的电子密度最低。随着功率的增大，电子密度值不断提高，但空间分布规律几乎不受影响。因为功率主要对加热区内的电子运动产生影响，使得碰撞电离作用增强，从而有效提高电子密度； 而功率对电子从加热场区域向四周扩散输运过程的影响较小，因此，电子密度的空间分布梯度基本不受影响。

图6为气压5 Pa时，电子温度在不同放电功率条件下的空间分布。为方便比较仿真结果，选取三维模型的剖面图进行分析。可以看出，随着功率增加，电子温度的峰值呈现小幅降低的趋势，分别为3.19 eV，3.15 eV和3.11 eV。电子温度的高低反映了等离子体中电子平均动能的大小，随着输入功率的增加，电子运动也随之加速，更加剧烈。由于电子碰撞中性粒子，导致电子能量的损失，因此，电子温度呈现小幅降低[15]。

图6 电子温度在不同放电功率下的空间分布Fig.6 Spatial distribution of electron temperature under different discharge power

图7为不同线圈功率下电势的空间分布。从仿真结果可以看出，线圈功率增加后，电势的峰值出现小幅减小。分析原因如下：放电功率的增加导致等离子体的趋肤深度减小，使得趋肤深度对等离子体电势的影响减弱，因此，电势的峰值随着功率的增加而减小。

图7 不同放电功率下电势的空间分布Fig.7 Spatial distribution of electric potential under different discharge power

为了可以更加直观分析等离子体的参数变化，在腔体z=2 cm处的横截面上选择了一条中心线作为参数提取的路径，如图8(a)所示。仿真得到气压为5 Pa时，不同放电功率下电子密度在腔体横截面参数提取路径上的分布，如图8(b)所示。可以看出，随着功率的增大，路径上的电子密度值整体呈增加趋势，且空间分布依然保持明显的梯度变化。

图8 不同功率下的电子密度分布Fig.8 Electron density distribution under different power

3.2.2 腔内气压对等离子体参数分布的影响

将放电功率固定在200 W，通过改变腔体内稀有气体的气压来研究其对等离子体参数分布的影响，气压为10 Pa，30 Pa和200 Pa时的电子密度分布如图9所示。可以看出，腔内气压从10 Pa增加到30 Pa，电子密度的峰值显著增加，从9.12×1017m-3上升到3.62×1018m-3； 当气压达到200 Pa时，电子密度峰值区域从腔体对称轴附近的位置压缩到线圈附近的加热区内。

图9 不同气压下的电子密度分布Fig.9 Electron density distribution under different air pressures

线圈功率固定条件下，不同气压下电子密度在腔体横截面参数提取路径上的分布如图10所示，该路径取自z=2 cm处的横截面上(见图8(a))。图10给出了放电功率为200 W时腔体内的电子密度分布情况。气压为30 Pa时，腔体中心区域的电子密度分布较为均匀，气压的升高使得电子密度明显增加； 当气压上升至200 Pa时，电子密度分布几乎不再变化。这是因为气压上升后，欧姆加热取代随机加热，功率耦合效率的有效提升使得电子密度增加，但过高的气压会导致电离率下降，从而使电子密度不再明显增加，甚至出现下降的情况。

图10 不同气压下电子密度在提取路径上的分布Fig.10 Distribution of electron density on the extraction path under different air pressures

从碰撞角度看，在低气压ICP放电中，起电离作用的电子平均自由程和放电区域的尺寸接近，因此，只需要注入一个小范围的电源能量，就可以获得较为均匀的空间分布[7, 16]。但在高气压下，放电区域的尺寸要大于电子平均自由程，在放电过程中各处的电离速率不均匀，导致电子密度的空间分布也出现明显不均匀现象。

4 结 论

本文在飞行器表面的等离子体隐身问题背景下，针对ICP放电问题，设计了一种方形透波腔体，利用流体力学理论建立了ICP模型； 在此基础上采用多物理场仿真软件COMSOL进行三维仿真，得到不同条件下感应耦合等离子体的放电特性。结果表明，感应耦合等离子体在低气压放电条件下通过改变线圈功率和气体压强，可产生高密度均匀的等离子体。气压不变，当线圈功率增加时，相应的等离子体参数分布变化明显，电子密度在增大的同时其空间分布也更加集中，而电势与电子温度则随着线圈功率的增加而减小。气压的增加使电子密度的峰值显著提高，但需要注意的是，当气压超过200 Pa的阈值时将不再对放电参数的分布有明显影响。综上所述，功率和气压在一定范围内增加有益于等离子体参数的分布，对于探究等离子体参数分布对电磁散射特性的规律并将ICP应用到工程实践中具有指导意义。