MEMS陀螺/半捷联稳定平台信息融合技术

蒋庆华，付奎生，丁海山

(中国空空导弹研究院，河南 洛阳 471009)

0 引 言

现代战争中，载机平台强调隐身能力，对机载武器提出了新的需求，要求机载武器内埋挂装。载机平台高密度挂装，要求尽可能增加挂装武器数量，并保证有足够大的威力[1]。为了更大限度地实现载机的作战任务，要求机载武器体积更小、重量更轻。空空导弹应用的特殊性和作战的高效性要求其弹体一直朝着小型化方向发展[2]，而作为重要组件的导引头也一直顺应该潮流。随着战场环境复杂化、任务多样化，提升导引头的探测识别能力、抗干扰能力变得越来越重要[3]，其中雷达/红外多模复合技术[4-5]、多波段复合技术[6]是提升探测、抗干扰的主要手段。相对于传统导引头结构而言，这些方法对结构的紧凑型也提出了更高的要求。导引头的小型化、紧凑化始终是机载武器技术发展的重要方向。

导引头稳定平台在结构形式与控制方法确定的前提下，导引头小型化主要有两个主要途径：采用半捷联技术和更小的MEMS陀螺。半捷联技术最早被应用在美国的AIM-9X导弹中[7], 同传统的速率陀螺式稳定平台比较，省去了稳定平台台体上的速率陀螺，平台的空间稳定与跟踪所需要的台体惯性角速度是利用弹体导航IMU中的高精度陀螺信息通过坐标变换与平台框架相对角速度合成得到，结构空间更为紧凑。目前的主要问题是框架角速度受到位置传感器精度的限制导致精度很差，提取框架之间的测速误差对视线角速度测量误差的影响较大[8]。MEMS陀螺采用准微电子的工艺制成，具有高集成度、小尺寸和重量轻的特点，其精度也一直在提升，已经在武器领域展示出其强大的生命力，但高端产品技术成熟度还比较低，目前处于技术转化阶段[9-10]目前，满足工程实际应用的MEMS陀螺与低精度传统陀螺相比，仍然存在噪声大、精度差的问题。因此，在保证小型化的同时降低误差是上述两种方案都急需解决的问题。

信息融合技术是常用的提升信号品质的手段，文献[11]利用稳定平台自带的MEMS传感器信号与探测信息进行信息融合，从而降低了MEMS传感器的低频漂移与高频噪声。实际在MEMS陀螺领域中，“虚拟陀螺”技术就是典型的利用冗余信息提升信号水平的手段。文献[12]通过MEMS陀螺的误差分析，设计了基于卡尔曼滤波的最优估计算法，并开展了相关的仿真和实验[13]。文献[14-15]的研究着重于陀螺数量的配比、位置的分布、陀螺之间的相关性等方面，以往虚拟陀螺技术主要应用于惯性导航领域[16-17]。在稳定平台控制方面，文献[18]最早提出了利用虚拟陀螺技术应用于稳定平台控制的设想，但并未针对平台控制的指标特性，结合方法付诸针对性分析和实现。

因此，开展将MEMS陀螺和采用半捷联技术同时配置于稳定平台中，对双源信号进行融合从而降低信号的噪声，具有一定的研究和工程意义。

1 速率陀螺稳定平台直接/半捷联稳定原理

图1为典型的航向/俯仰两轴速率陀螺式红外导引头平台结构[19]。弹体上固联有导航用IMU，包括敏感弹体运动的三轴陀螺，基座支架与弹体装配固联，基座支架通过航向驱动电机和航向测角器与偏航框架构成航向方向可转动连接，偏航框架通过俯仰驱动电机与俯仰测角器与俯仰负载构成俯仰方向可转动连接。俯仰负载上固联有光学镜头、探测器。为了更好地跟踪目标，导引头平台需要良好的隔离导弹弹体运动的能力，因此以往的导引头负载上需要固联有速率陀螺，直接敏感光轴的惯性角速度，构成图2所示的直接稳定控制方案。由于陀螺安放在负载上，处于框架中心，负载的尺寸和重量直接决定了稳定平台整体的尺寸，因此如果采用小型的MEMS陀螺则能够大幅削减空间。半捷联控制方式省去了负载上的陀螺器件，利用弹体上IMU中的陀螺和测角器信息组合构成负载的惯性角速度信号，形成图3所示的控制方式[20]。

图1 典型光学导引头稳定平台结构示意图Fig.1 Typical structure of optical seeker stabilization platform

图2 平台直接稳定控制Fig.2 Direct stability control of platform

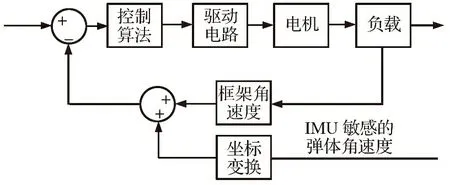
图3 平台半捷联稳定控制Fig.3 Semi-strapdown stability control of platform

2 半捷联信息特征分析

(1)

(2)

则负载的角速度为

(3)

(4)

从式(4)可以看到，半捷联方式构造的负载角速度是弹体IMU敏感的弹体角速度与框架角、框架角速度的函数。陀螺的噪声、框架角、框架角速度对信号噪声均有贡献。

下面对各个部分的噪声特性进行逐一讨论。

弹载陀螺通常采用光纤陀螺，光纤陀螺的随机误差主要包括角速度随机游走、速率随机游走[12, 22]，表述为

ω=ω0+b+na

(5)

伺服控制系统的测角器通常包括电位计、编码器和旋转变压器，其中电位计和编码器原理上都是纯测角传感器。角速度信号通过信号差分求得，角度信号的随机误差主要由接口电路1/f噪声引起，角速度信号的精度还与采样周期相关，如果要得到与陀螺角速度相当的速度信号和带宽则需要很高的精度。旋转变压器则采用跟踪闭环检测的方式可以直接得到框架角速度。

旋转变压器为磁性元件，依靠载波驱动原边，转子、定子相对位置变化时，动边的感应磁场反映了角度的变化。因此元件本身不具有随机信号的特征，随机误差主要体现在接口电路上。目前，常用的闭环跟踪系统通过包含锁相环的电路构成，从电路的原理可以确认其电路的主要噪声由锁相环的压控振荡器频率稳定性与后续A/D的转换引起，其中锁相环的相位、频率稳定性直接影响其输出噪声。旋转变压器速度跟踪实现如图4所示。

图4 旋转变压器速度跟踪实现Fig.4 Velocity tracing scheme of resolver

3 半捷联信息、MEMS陀螺误差分析建模

随机噪声误差的分析与建模通常包括功率谱方法、自回归分析方法、Allan方差分析方法等。

Allan方差分析方法源自于分析振荡器的相位和频率不稳定性，因此更适合分析旋转变压器电路中的锁相环频率不稳定性噪声特性； 而目前Allan方差分析方法也是惯性传感器随机噪声分析的最常见方法[23-24]，因此本文采用Allan方差分析方法进行误差的建模与分析。

陀螺的Allan方差分布如图5所示。Allan方差曲线从左至右随着采样时间的延长，斜率逐渐从负数变为正数，左半边区域反映了信号的高频特征，右半边反映了信号长时间运行后的低频特征。

图5 陀螺的典型Allan方差分布Fig.5 Allan variance curve of gyroscopes

假定各项随机误差在统计意义上相互独立，则总的Allan方差可以表述为各项随机误差的Allan方差之和：

(6)

式中：τ为采样时间间隔；Q为量化噪声系数；N为角度随机游走系数；B为零偏不稳定性系数；K为速率随机游走系数；R为速率斜坡系数。

由于导引头稳定平台为快速时变信号，因此短时间(60 s)采用Allan方差分析方法分别对半捷联信号以及MEMS陀螺输出信号进行分析。图6为从实际样机中静态采集的半捷联信号，图7为Allan方差结果。可以看到在采样时间很短的时候曲线有峰值，与标准的方差曲线不同。对半捷联信息进行频谱分析，如图8所示。可以看到信号中包含了某些较窄频率点的噪声，这些噪声可以通过陷波器进行消除。采样得到的整个曲线的整体趋势为随着采样时间的增加，方差逐渐缩小，斜率大于等于0的误差项均未表现出来，即在导引头所涉及的时间范围内，所采用传感器的随机误差只有角度随机游走为主导。

图6 半捷联信号时域曲线Fig.6 Time domain curve of semi-strapdown signal

图7 半捷联信号Allan方差曲线Fig.7 Allan variance curve of semi-strapdown signal

图8 半捷联信号频谱特性Fig.8 Frequency character istics of semi-strapdown signal

图9为同时静置与转台的MEMS陀螺输出时域信号，其Allan方差曲线如图10所示。可以看到其符合方差的典型趋势，同半捷联信号特征一样，短时内噪声以角度随机游走为主导。

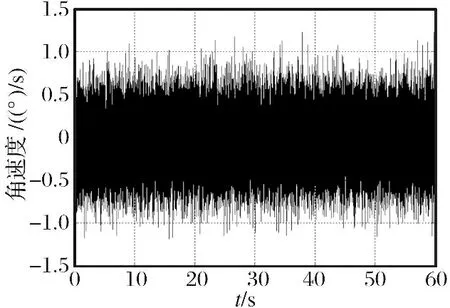
图9 MEMS陀螺时域曲线Fig.9 Time domain curve of MEMS gyroscope

图10 MEMS陀螺Allan方差曲线Fig.10 Allan variance curve of MEMS gyroscopes

4 MEMS陀螺/半捷联信息融合

根据上文对MEMS陀螺和半捷联随机噪声实测数据的分析以及导引头对角速度信号实时快速性的应用特点可以明确，角度随机游走为信号随机噪声的主导项，其他项可忽略，因此将两者的输出信息统一定义为真实角速度信号与角度随机游走的和：y=ω+na。ω为真实角速度信号；na为白噪声特性的角度随机游走。

MEMS陀螺/半捷联信息系统的状态方程和量测方程定义如下：

(7)

对应的离散方程为

(8)

基于卡尔曼滤波的计算方法可以得到如图11所示的MEMS陀螺/半捷联信息融合系统图。

图11 MEMS陀螺/半捷联信息融合系统Fig.11 MEMS gyroscopes and semi-strapdown signal fusion system

为了讨论方差阵中关键参数对滤波器的影响，采用连续卡尔曼滤波的手段对稳态值进行分析，根据稳态卡尔曼滤波方程[25]，可以得到MEMS陀螺和半捷联滤波器的连续方程：

(9)

对式(9)第一个公式进行拉普拉斯变换，则得到其传递函数可表示为

(10)

相当于一阶系统增益K决定了带宽的大小。

(11)

(12)

当qω=q=1时，稳态方差P∞与等效带宽系数KH随ρ和g变化的二维图如图12所示。可以看出，当半捷联信号与MEMS信号噪声水平相当时，P∞随着相关系数从-1～+1逐渐增大，同时带宽系数越来越小； 当半捷联信号与MEMS信号噪声水平相差较大时，P∞存在一个从递增到递减的过程，带宽系数KH则表现为递减再递增的过程。

图12 归一化方差P∞、带宽系数KH随ρ和g变化趋势Fig.12 Plot of P∞, KH varying with ρ and g

5 离线仿真

为了验证融合滤波的效果，在Simulink中建立了离线仿真模型，如图13所示。真实信号用正弦信号模块产生，各自叠加离线采集的静态噪声信号后模拟传感器的最终输出信号。根据之前的数据分析结果，半捷联信息等效角度随机游走0.99 (°)/h1/2，MEMS陀螺角度随机游走为0.65 (°)/h1/2, 相关系数为0，仿真时设定实际输入信号的角加速度噪声为200 (°)/h3/2。

图13 基于Simulink的离线数据仿真模型Fig.13 Simulation model of off-line data based on Simulink

当输入角速度为0时，采用三组不同的离线数据进行前后对比，如图14所示。滤波信号以及滤波前MEMS陀螺和半捷联信号的标准差分别为：0.074 5，0.297 5，0.385 3； 0.069 8，0.320 7，0.356 9； 0.061 9，0.312 9，0.375 9。方差平均降低为原来的1/4，噪声的方差大大减小。

图14 滤波前后的静态时域信号Fig.14 Comparison of original data vs fusion data of zero input

当输入1 (°)/s，10 Hz正弦角速度时，滤波效果明显，幅值和相位均无明显的改变，如图15所示。当频率增加50 Hz时，幅值衰减为输入的50%。因此，按照目前的传感器噪声水平和相关度，滤波信号只能够提供作为制导信号的参考，尚不满足伺服控制的闭环需求。

图15 滤波前后的动态时域信号Fig.15 Comparison of original data vs fusion data of sine input

6 结 论

本文基于MEMS陀螺和半捷联信息的信号特征，构建了集成两者的信号级融合滤波系统，离线仿真数据表明，不相关、滤波后的信号比原始信号噪声大幅降低。引入信号的噪声比例系数与相关系数进行的融合系统稳态特性分析表明，滤波的效果与带宽两个系数非单调性相关变化，该结论具有一定的工程参考意义。文中使用的离线数据滤波后可用于制导信息的参考，在实际工程应用时，若能够根据系统特性构造出合适的相关系数，将达到更好的滤波融合效果。