中低空太阳能无人机高效螺旋桨设计方法

邱辉壮，江善元，钟伯文

（南昌航空大学飞行器工程学院，南昌 330063）

0 引 言

近年来，随着无人机技术的发展，其被广泛应用在电力巡检、边境巡逻、航拍测控和农业植保等各行各业中，然而在实际的应用中，无人机长航时续航能力不足的问题日益显著。随着光伏技术的快速发展，太阳能无人机有望成为解决续航问题的突破点，目前，高空长航时太阳能无人机得到了一定程度的发展，但是达到真正实现高空长航时飞行的商业应用仍存在一定的距离，而将太阳能无人机技术引入中低空民用领域在现阶段具有较大的可能性。如何对太阳能无人机吸收的能量进行合理高效利用一直是大多数研究者的研究重点，进行适用于中低空太阳能无人机高效率螺旋桨的设计研究是达成这一目标的重要技术手段之一。

国外，S.D'Angelo等提出一种在给定工况下设计高效率螺旋桨的方法；O.Gur等提出计算基于低前进比设计螺旋桨的性能方法；Q.R.Wald将最小能量损失原则应用在小型螺旋桨设计上。国内，曹潇等总结了当前低空太阳能无人机的研究现状及其需要攻克的关键技术；刘远强等开发了一款基于片条理论计算螺旋桨性能的程序；李星辉等采用对低雷诺数高升力翼型优化的方法，进行适用于高空长航时飞行的高效率螺旋桨研究；郭佳豪等结合数值模拟CFD方法，提出一种螺旋桨快速迭代修正设计方法；唐伟等采用车载试验和数值模拟相结合的方法，对基于单一设计点和两个设计点的螺旋桨特性进行分析研究。此外，还有研究者通过改变桨叶积叠方式、提高螺旋桨加工工艺等工程方法，对现有螺旋桨进行快速优化设计。综上所述，目前多数研究集中在常规螺旋桨和高空螺旋桨设计，对中低空太阳能无人机螺旋桨的研究鲜见。

本文根据某型中低空太阳能无人机的飞行任务包线，提出一种基于最小能量损失准则与片条理论及其逆向推导的设计方法，对多设计点下的高效螺旋桨进行设计，并使用CFD数值模拟方法对设计螺旋桨进行气动力求解与分析。

1 螺旋桨设计理论

高效螺旋桨的设计难点在于确定合理的弦长分布和桨距角分布。径向处的叶素受力分析和速度分解图如图1所示，其中为几何入流角，为实际入流角，为叶素与来流的有效迎角，为滑流引起的干涉角，为翼型的阻升角，'为诱导螺距，为轴向诱导速度，为环向诱导速度，为几何入流速度，为实际入流速度，d与d为叶素的升力和阻力，d与d为叶素的拉力和扭力、d为叶素合力。

图1 螺旋桨叶素受力分析图Fig.1 Propeller element forces

在给定设计工况下，已知来流速度，螺旋桨设计转速和设计拉力，求解各叶素的弦长和桨距角的具体步骤如下：

（1）确定桨叶数和桨叶半径，沿着径向方向将桨叶划分成个叶素剖面，确定各叶素的翼型。

（2）基于最小能量损失确定诱导螺距'及桨叶的最佳环量分布。

在螺旋桨桨叶径向处，当叶素环量产生Δ的增量扰动时，分别给螺旋桨带来Δ和Δ大小的拉力与扭矩的增量变化，将这一增量带来的有用功与吸收能量的比值用能量比表示为

由涡流理论可知，Δ的环量增量带来的拉力及扭矩的变化分别为

将式（2）～式（3）带入式（1），可得：

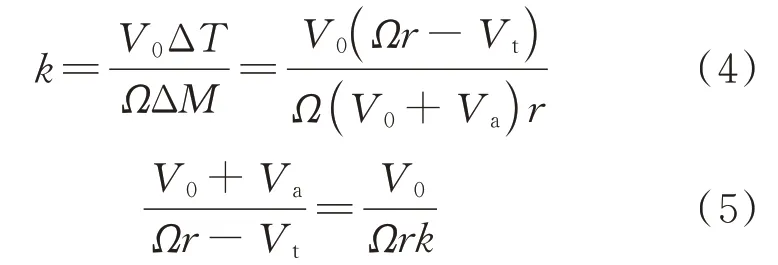
要使得螺旋桨效率最高，需要在值大的地方增加环量，在值小的地方减小环量。因此螺旋桨环量分布最优的条件是值在桨叶展向方向保持不变。

根据图1速度分解几何关系可以得到：

由式（5）和式（6）可得：

根据几何关系得到：

按照涡流理论的推导方法，在桨盘处可以得到诱导速度与环量，来流速度，诱导螺距'和桨叶数的关系如式（9）～式（10）所示。

轴向诱导速度：

环向诱导速度：

联立式（8）～式（10），简化提出环量值，可以得到环量的表达式：

通过式（11）在径向处建立起环量与来流速度，诱导螺距'，螺旋桨转速及桨叶数的关系。

假设给定的设计拉力为，则环量分布的大小需要满足设计拉力。

将整个桨叶的环量折合成拉力并沿径向进行积分，即式（11）、式（12）带入式（13），迭代求解出满足设计拉力的诱导螺距'，从而确定最佳环量分布()。

（3）在最佳环量分布基础上，结合片条理论对其逆向推导，求解出叶素的弦长和桨距角。

片条理论的核心在于求解滑流引起的干涉角，结合动量理论与叶素理论可以推导出隐式方程：

其中：

采用Newton迭代法求解式（14）～式（17），可以得到干涉角。

则桨距角：

叶素环量可表示为

假设在径向处选定翼型升力系数为C ，阻力系数为C ，环量()由式（11）确定，即可以计算出叶素弦长的大小。

（4）重复步骤（2）和步骤（3），得到所有剖面叶素的几何参数。

（5）结合太阳能无人机的飞行高度曲线，对不同设计点的求解参数进行权值分配，得到最终的桨叶弦长分布和桨距角分布。

为了使理论设计更加符合工程实际，设计过程需要考虑有限桨叶数引起的桨尖损失，采用Prandtl修正因子进行桨叶数修正。

其中：

根据确定的螺旋桨来流速度、转速和桨叶数，可以求出不同径向处的修正因子。

式中：'为经过诱导因子修正后的诱导螺距，表征受三维效应引起的实际诱导损失。

将修正后的'代入式（11）的环量表达式中，即可得到修正后的基于最小能量损失有限桨叶数的最佳环量分布。

2 太阳能无人机高效螺旋桨设计

2.1 设计状态

本文研究的某型中低空太阳能无人机的飞行高度在海拔3 000 m以下，太阳能电池片能够提供240～350 W的实时输出功率，一个白昼任务周期内的飞行跨度曲线如图2所示。太阳能无人机的飞行策略受限于太阳辐射能的影响，根据需要调整飞行姿态，主要由爬升、2.5 km高度巡航、1.5 km高度巡航和下降四个阶段组成，下降阶段主要利用高度变化的势能差转换成飞行器飞行所需的能量，电机功率需求较小，因而不将其作为考虑的设计点。

图2 任务周期内的飞行跨度曲线示意图Fig.2 Schematic diagram of the flight span curve during the mission period

整机的升阻比约为32，设计螺旋桨桨叶数=2，单个螺旋桨半径=0.3 m，不同设计点对应的设计指标如表1所示。

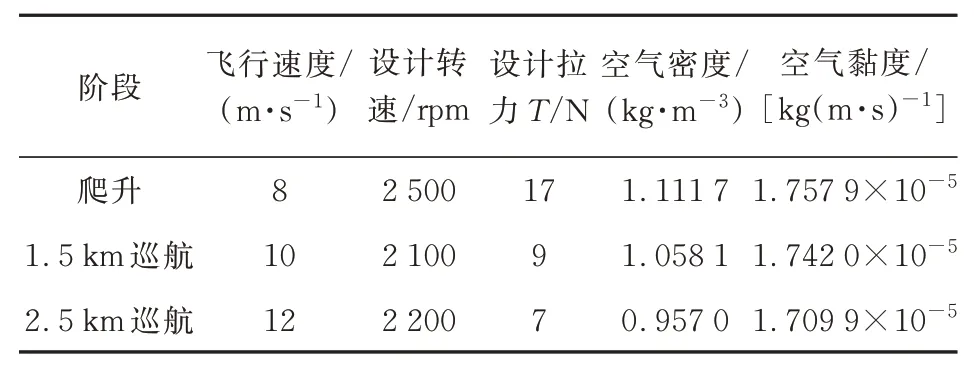
表1 不同设计点参数Table 1 Different design point parameters

2.2 设计步骤

（1）翼型的选择

根据螺旋桨的设计要求，对目前低雷诺数高升力翼型的研究成果进行分析表明，适用于低雷诺数工况螺旋桨设计的翼型有RAF 6、Clark Y、S1223和Eppler系列等。本文采用基于高阶面元法的Xfoil软件对翼型在雷诺数为15万量级下进行气动力计算，结果如图3所示，可以看出：Clark Y翼型在较大的迎角范围内具有较高的升阻比，翼型失速特性好。此外，Clark Y翼型后缘规整下表面较为平坦，便于实际的加工制作，在综合气动性能与加工难易程度等因素下，本文选取Clark Y翼型用作螺旋桨后续的设计工作。

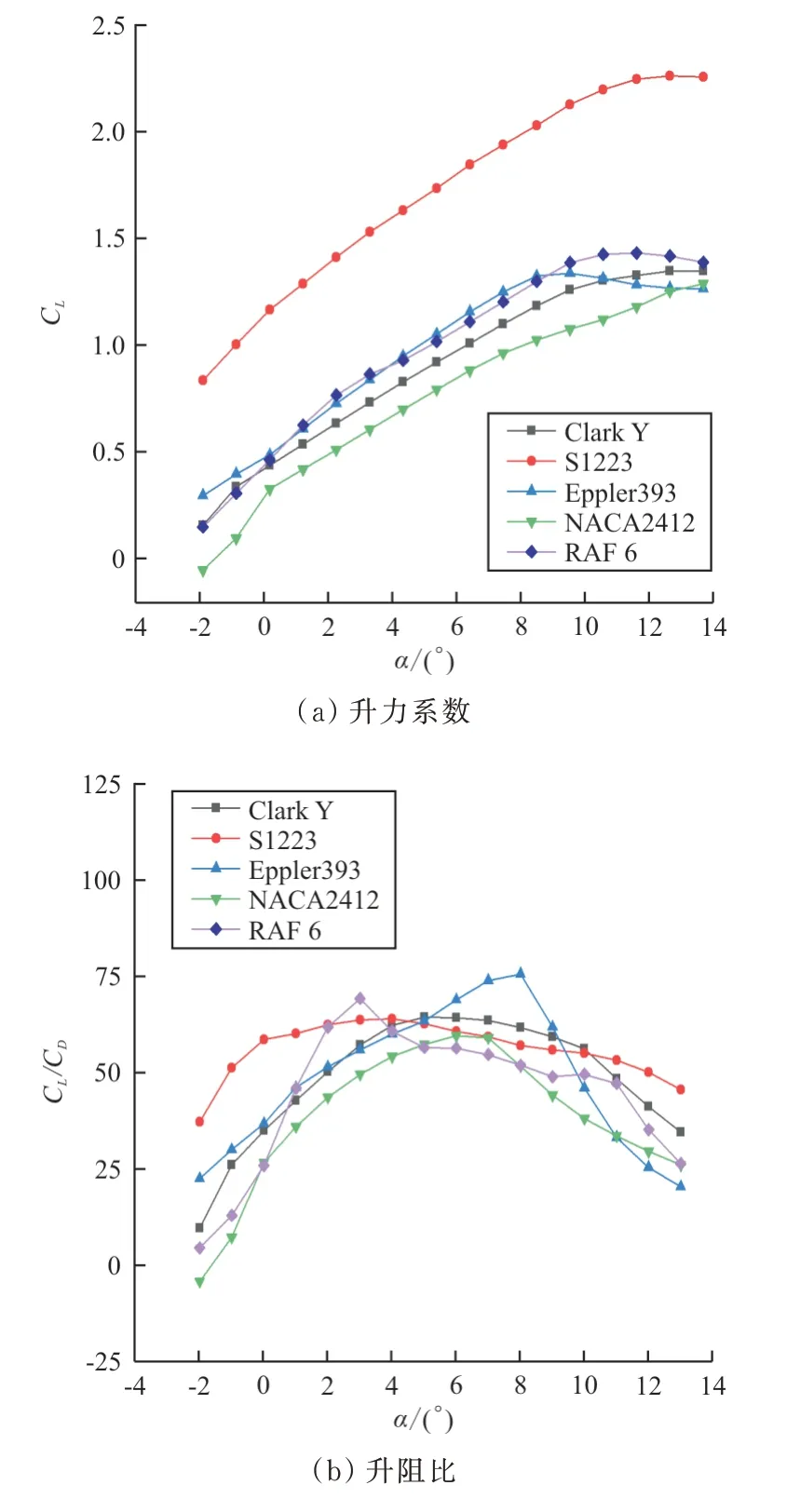
图3 翼型升力系数与升阻比对比Fig.3 Comparison of airfoil lift coefficient and lift-to-drag ratio

（2）求解不同设计点下的几何参数

根据螺旋桨设计理论，首先基于最小能量损失设计准则求解最佳环量分布，如图4所示，然后依次计算出三个不同设计工况下的弦长与桨距角分布，结果如图5所示。

图4 不同设计点下的最佳环量分布Fig.4 Optimal circulation distribution under different design points

图5 不同设计点弦长与桨距角分布对比Fig.5 Comparison of chord length and pitch angle distribution at different design points

（3）参数计算

为提高设计螺旋桨在整个任务曲线内的续航时间，需要平衡好各个设计点的计算结果，本文采用权值分配的方法，在分别计算出不同设计点的弦长与桨距角分布情况下，根据太阳能无人机爬升、1.5 km巡航和2.5 km巡航状态占某夏至日白昼12 h任务曲线的时间约为2、6和4 h，确定三个设计状态在整个设计过程中的权值分配值为0.17、0.50、0.33，将各设计点的弦长与桨距角按照以上分配权值进行加权计算，得到最终加权平均后的弦长与桨距角分布如图6所示。与常规螺旋桨相比较，沿着桨叶展向，设计的螺旋桨桨距角变化范围较大，桨尖弦长更小。

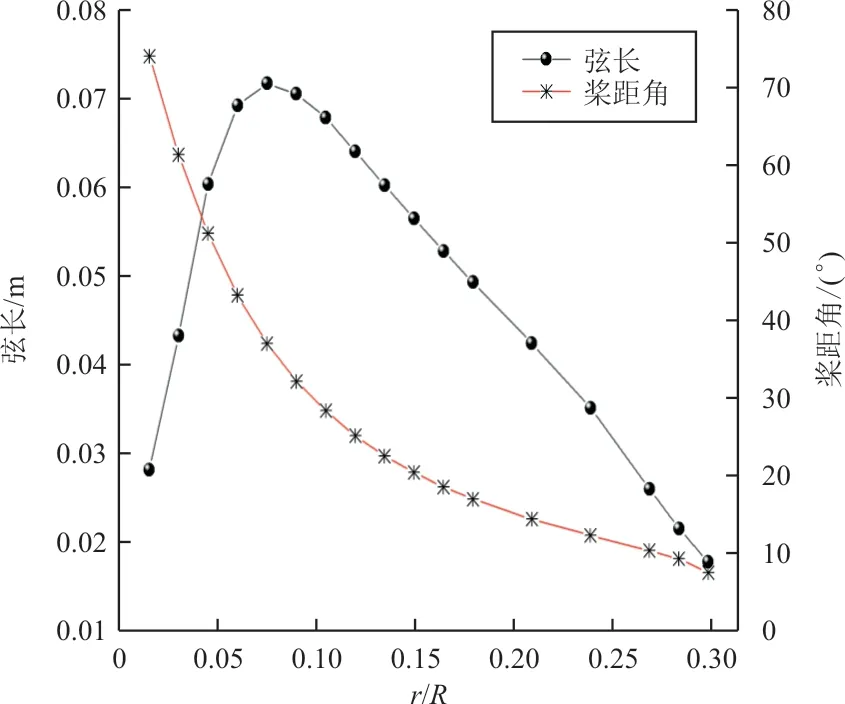
图6 弦长与桨距角的径向分布Fig.6 Radial distribution of chord length and pitch angle

为使设计桨叶几何光滑，采用4阶贝塞尔曲线对离散的弦长和扭转角分布进行拟合，CATIA创建的螺旋桨三维模型如图7所示。

图7 螺旋桨CATIA模型Fig.7 CATIA model of propeller

3 螺旋桨设计结果分析

3.1 数值模拟方法及网格无关性验证

选取一款与设计桨叶具有相似几何的常规螺旋桨进行逆向建模，该型螺旋桨半径=0.305 m，桨叶数=2，选取海拔1.5 km巡航高度的大气参数作为数值计算的环境参考值，具体大气物理属性如下：压强=84 559.6 Pa，密度=1.058 1 kg/m，黏度=1.742 0×10kg/（m·s），当地声速=334.5 m/s。数值模拟采用商用CFD软件的Fluent完成，计算域由圆柱体状外流域和包含桨叶几何模型的饼状旋转域组成，两流域之间采用共享拓扑设置，保证两流域之间能量和流动的交互，考虑到桨尖压缩性的影响，需要对桨叶的前后缘及桨尖处进行局部加密处理，在物面生成1/10弦长高度的附面层网格，几何模型与局部网格示意图如图8所示。

图8 流体区域与局部网格示意图Fig.8 Schematic diagram of fluid region and local mesh

基于MRF方法，定常求解雷诺时均N-S方程和SST-两方程湍流模型，采用压力—速度耦合SIMPLE的求解方法，离散格式均采用二阶迎风插值格式。在来流速度=10 m/s，螺旋桨转速=2 000 rpm的工作状态下，对模型进行网格无关性验证，分别改变桨叶网格尺寸3、5、7和9 mm，对应的体网格尺寸为301万、285万、259万和237万。螺旋桨拉力与扭矩的网格无关性曲线图如图9所示，当桨叶面网格尺寸小于5 mm（体网格285万）时，拉力与扭矩值波动很小，因而选取桨叶面尺寸5 mm用于模型的网格划分与计算。

图9 网格无关性验证Fig.9 Mesh independency verification

3.2 螺旋桨模拟计算结果校核

在实际工程中，除了使用数值模拟方法进行螺旋桨性能计算之外，风洞试验也是计算螺旋桨气动性能的重要方法之一。采用3.1节所述数值模拟方法，计算常规旋桨在来流速度=10 m/s，前进比0.39～0.55范围内的拉力与扭矩，同时在南昌航空大学NH-1风洞中对该桨叶进行风洞试验（如图10所示）。

图10 风洞中的螺旋桨（直径0.61 m）Fig.10 Propeller in the wind tunnel（diameter is 0.61 m）

不同前进比下，模拟计算与风洞试验的数据对比如图11所示，可以看出：随着前进比的增大，两种方法计算出的与变化趋势一致，数值模拟的计算值略大于风洞试验值，且误差范围保持在5%～8%范围内，与文献［15-16］结论相同。数值模拟的计算结果符合计算的精度要求，可以用于设计螺旋桨气动性能的仿真计算。

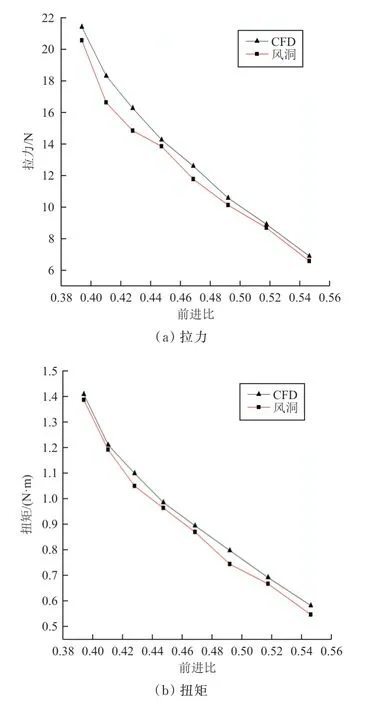
图11 数值计算与风洞试验结果对比Fig.11 Comparison of numerical calculation and wind tunnel test results

3.3 结果分析

基于3.1节验证的数值计算方法和网格划分尺寸，对设计螺旋桨进行模拟仿真计算，其中效率由式（24）计算得出。

计算结果如表2所示，可以看出：在相同转速下，随着来流速度的增加，拉力与扭矩均减小。在太阳能无人机能够提供的实时功率范围内，设计螺旋桨在三个设计点处对应的拉力分别为20.367、8.486和8.675 N，满足设计要求。其中，爬升阶段效率最大为68%，在1.5和2.5 km高度巡航阶段，螺旋桨在允许功率范围内能够保持较高效率，=10 m/s，转速2 000 rpm时效率达到73.2%；=12 m/s，转速2 200 rpm时效率达到73.5%。

表2 螺旋桨数值计算结果Table 2 Numerical calculation results of propeller

设计螺旋桨与常规螺旋桨分别在爬升（=8 m/s，前 进 比0.3～0.5）和巡航阶段（=12 m/s，前进比0.44～0.66）的效率对比如图12所示。

图12 常规螺旋桨与设计螺旋桨效率对比Fig.12 Comparison of efficiency between conventional propeller and design propeller

从图12可以看出：设计螺旋桨效率提升明显，且效率随着前进比变化的波动幅度较小。

4 结 论

（1）本文提出了一种中低空太阳能无人机高效螺旋桨的设计方法，求解出螺旋桨合理的弦长与扭转角分布并建立了三维模型，基于验证的数值模拟方法对设计螺旋桨的气动性能进行仿真求解。

（2）设计螺旋桨的性能满足设计要求，在允许功率范围内，与类似尺寸的常规螺旋桨相比较，在飞行包线内的效率提升明显，其中，巡航阶段效率最大提升13%左右。

（3）本文提出的高效螺旋桨设计方法具有较高的应用价值，对未来中低空太阳能无人机螺旋桨的设计具有一定的指导意义。