民用客机可变弯度机翼优化设计研究

郝璇，张青青，苏诚，王斌

（中国航天空气动力技术研究院第二研究所，北京100074）

0 引 言

降低巡航阻力是民用客机气动设计追求的重要目标。机翼的阻力占民用飞机总阻力的一半左右，对性能和飞行品质有着至关重要的影响。传统民用客机超临界机翼气动设计通常需要兼顾非设计点或其他要求，导致飞机最优巡航气动效率损失。此外，随着民航业繁荣发展，空域越来越拥挤，飞机难以在整个巡航阶段按照设计状态飞行，在一定程度上增加了燃油消耗。

如何使民用客机在非设计状态仍能保持较高的升阻比是进一步提高飞机巡航效率必须解决的问题。可变弯度机翼无论是从基础空气动力学还是实际飞行应用的角度都具有巨大潜力，已成功应用于军用飞机。由于民用客机要考虑低成本、高可靠性等要求，工业界对该技术进行了长期的探索和论证。NASA Dryden飞行研究中心基于L-1011飞机首次开展了可变弯度机翼技术应用于民用客机的减阻收益研究。Boeing和Airbus从20世纪80年代开始评估变弯度概念，前者在B777-200ER上进行了后缘变弯度飞行试验，后者针对A330/340开展了变弯度预设计，最终成功将该技术应用于新一代远程宽体客机B787和A350，在巡航时通过小角度偏转襟翼与扰流板，改变机翼后缘弯度，改善气动载荷分布，优化了巡航状态的阻力特性。

国内对变弯度机翼技术的研究起步较晚，随着国产远程宽体客机论证及立项，国内高校、科研院所也相继开展了变弯度机翼气动优化设计研究。梁煜等针对大型民用运输机，开展了超临界翼型后缘变弯度优化研究；郭同彪等基于自由型面变形技术建立后缘连续变弯度参数化模型，研究了后缘连续变弯度对跨声速翼型及机翼气动特性的影响；王斌等基于展向控制翼型建立了一种简化的理想变弯度模型，对超临界机翼变弯度减阻原理进行了研究；郭同彪等采用伴随技术对翼—身—平尾构型后缘连续变弯度减阻进行了优化。目前国内的研究工作多针对二维翼型或采用基于控制截面翼型变弯度的简化模型，与实际工程中机翼变弯度实现形式有一定差距。此外，变弯度优化均针对特定飞行状态进行，而在实际飞行中气动力特性不断变化，如何实施有效的变弯度操作以获得理想的减阻效果仍需要进一步研究。

针对上述问题，本文充分考虑实际工程约束，基于襟翼、扰流板运动建立变弯度模型，以全机配平构型为研究对象，研究机翼后缘弯度变化对平尾配平特性产生的影响；采用RANS方程作为数值求解方法，建立响应面模型，对包括不同升力系数、马赫数的多个飞行状态进行变弯度减阻优化并对实际飞行过程中变弯度操作需求及综合减阻性能进行分析。

1 变弯度研究模型

研究表明，机翼后缘变弯度影响平尾配平特性。为充分考虑这种影响带来的不利因素，本文以翼身组合体—短舱—吊挂—垂平尾构型为研究对象，该构型巡航马赫数=0.85，升力系数C =0.48。干净机翼多个设计点如表1所示，其中设计点1～3优化阻力发散特性，设计点2、4兼顾抖振特性。

表1 干净机翼设计点Table 1 Design point of the wing

参考现役宽体客机平面布置，生成襟翼、副翼、扰流板等变弯度关键部件，如图1所示。

图1 可变弯度机翼研究模型Fig.1 Camber variable wing model

襟翼展长为机翼翼展的75%，相对弦长为机翼当地弦长的10%～25%。采用铰链机构实现襟翼偏转，通过小角度偏转内、外襟翼实现机翼弯度变化。扰流板简化为内、外两块，随襟翼偏转而运动。通过偏转升降舵实现不同状态变弯度外形的配平。

2 数值优化方法

2.1 数值模拟方法

本文计算采用可压缩流动Reynolds平均Navier-Stokes方程。为精确计算机翼弯度改变前后的气动力变化情况，采用点对点结构网格，计算网格如图2所示，半模网格数量为1 900万。计算域内近壁面第一层网格高度为5×10m，保证壁面＜1。本文采用--SST模型，计算中使用多重网格技术加速收敛。为保证计算精度，对数值方法进行较为全面的验证，具体方法详见文献［21-22］。

图2 计算网格示意图Fig.2 Sketch of computational grid

2.2 基于代理模型的优化方法

整个优化设计流程如图3所示。本文以全机配平构型为研究对象，以内、外襟翼偏角为优化对象，全机配平构型阻力最小为优化目标。其中，内襟翼偏转范围为［-1°，3°］，外襟翼偏转范围为［-2°，3°］，向下偏转为正。考虑到实际飞行时，襟翼可偏转最小角度间隔为0.5°，因此，采用打靶法生成样本点。基本样本点在内、外襟翼偏转范围内，各1°偏角间隔。根据基本样本点结果，选取局部区域以0.5°偏角间隔进行加密。

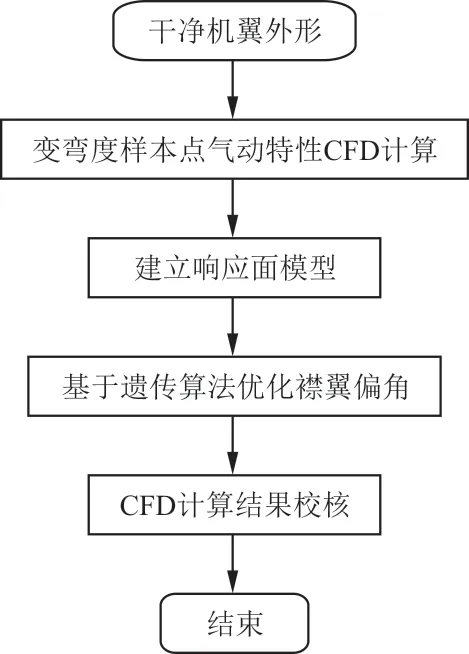
图3 可变弯度机翼优化设计流程Fig.3 The optimization process of the variable camber wing

基于样本点数值模拟结果，采用响应面方法（Response Surface Methodology，简称RSM）建立代理模型。该方法利用多项式函数拟合设计空间，通过较少的试验在局部范围内比较精确地逼近函数关系，具有良好的鲁棒性。基于响应面模型，首先采用遗传算法对襟翼偏角进行优化，然后采用CFD数值模拟对优化结果进行校核，获得精确减阻量。

3 可变弯度机翼优化设计

3.1 巡航设计点：M a=0.85，C L=0.48

首先对基本样本点全机配平构型气动特性进行数值模拟。采用阻力系数单位“cts”（1 cts=0.000 1）表示阻力系数大小，基本样本点全机配平构型与未变弯度全机配平构型阻力系数差量云图如图4所示，为内襟翼偏角，为外襟翼偏角，可以看出：在内襟翼［-1°，1°］、外襟翼［0°，1.5°］范围内，阻力系数差为负值，具有减阻潜力。

图4 巡航设计点基本样本点全机配平构型阻力差量云图Fig.4 The drag dispersion contour at cruise point

根据基本样本点数值模拟结果，在［0°，1°］范围内增加4个样本点，样本点中阻力最小点对应的内、外襟翼偏角均为0.5°，相比未变弯度状态，阻力系数降低0.82 cts。以33个样本点建立2阶响应面模型，以全机配平构型阻力最小为优化目标对内、外襟翼偏角进行优化。优化得到的内、外襟翼偏角分别为0.41°和0.61°，相比未变弯度状态，阻力系数降低0.91 cts。样本点最优阻力系数与优化结果相差不到0.1 cts。样本最优阻力点与优化结果的展向压力分布如图5所示，样本最优阻力点与优化结果的升力系数与载荷系数分布如图6所示，可以看出：在拐折和外襟翼区域，激波强度轻微减弱；后缘变弯度使中外翼区域载荷有所增大。

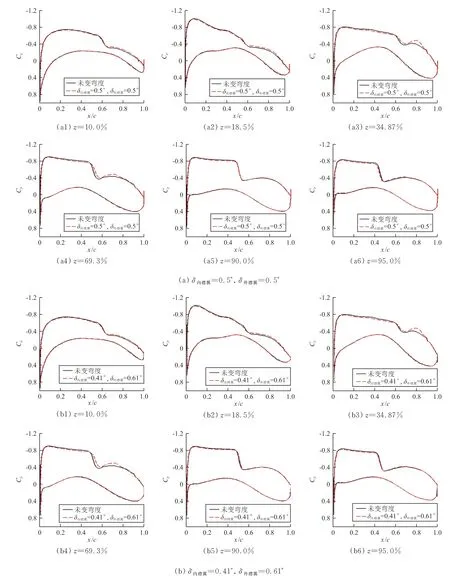
图5 M a=0.85，C L=0.48展向截面压力分布Fig.5 The sectional pressure distribution along the wing at M a=0.85，C L=0.48

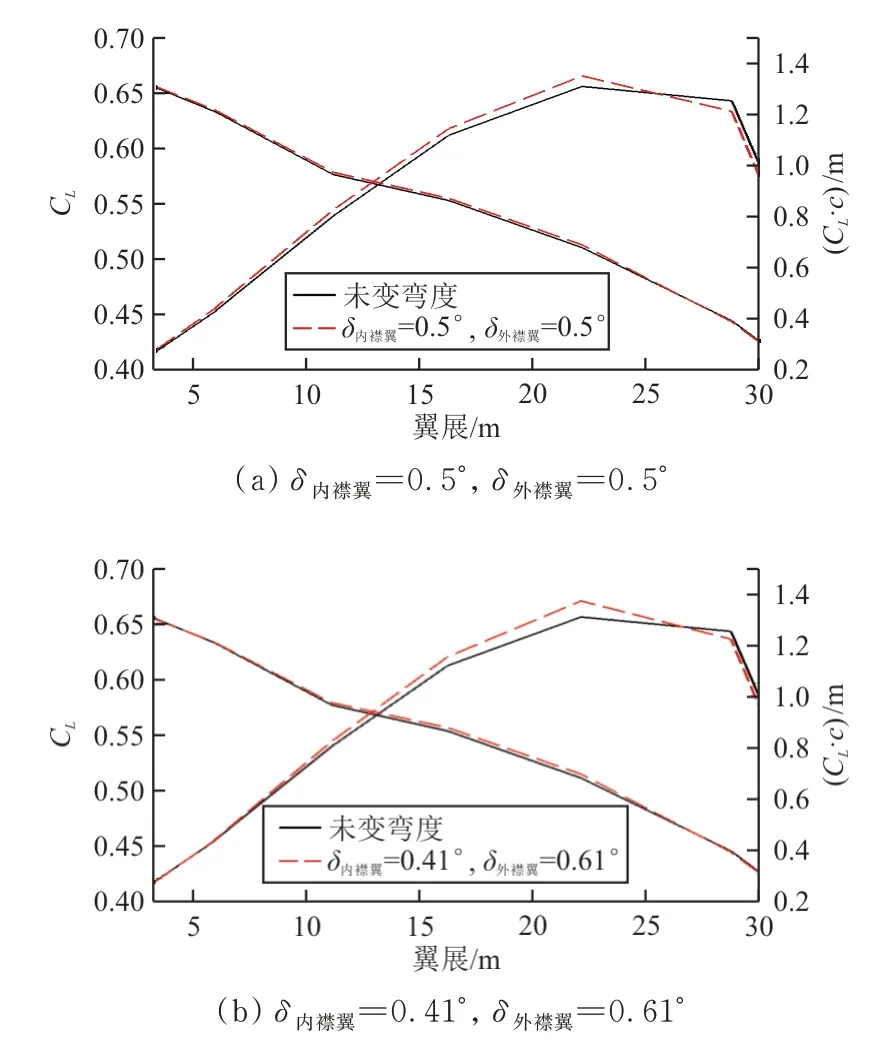
图6 M a=0.85，C L=0.48展向载荷系数分布Fig.6 The load coefficient distribution along the wing at M a=0.85，C L=0.48

3.2 非设计点1：M a=0.85，C L=0.52

基本样本点全机配平构型与未变弯度全机配平构型阻力系数差量云图如图7所示。

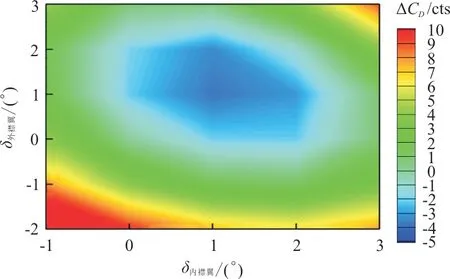
图7 非设计点1基本样本点全机配平构型阻力差量云图Fig.7 The drag dispersion contour at off-design point 1

从图7可以看出：在内襟翼［0°，2°］、外襟翼［0°，2°］范围内，阻力系数差量为负值，具有减阻潜力。

根据基本样本点数值模拟结果，在［0°，2°］范围内增加了7个样本点。样本点中阻力最小点对应的内、外襟翼分别为1.5°和1.0°，相比未变弯度状态，配平后阻力系数降低3.88 cts。以36个样本点建立2阶响应面模型，以全机配平构型阻力最小为优化目标对内、外襟翼偏角进行优化。优化得到的内、外襟翼偏角分别为1.24°和1.22°，相比未变弯度状态，阻力系数降低3.93 cts，样本点最优阻力系数与优化结果相差不到0.1 cts。

样本最优阻力点与优化结果的展向压力分布如图8所示，样本最优阻力点与优化结果的升力系数与载荷系数分布如图9所示。

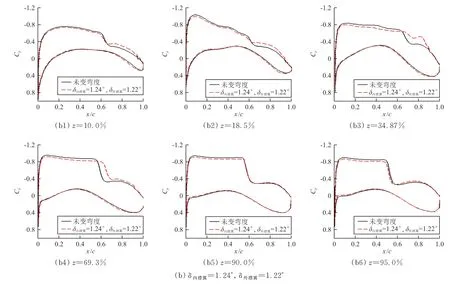
图8 M a=0.85，C L=0.52展向截面压力分布Fig.8 The sectional pressure distribution along the wing，at M a=0.85，C L=0.52

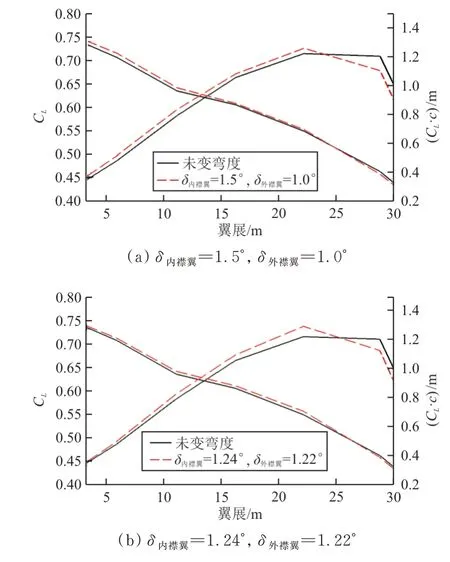
图9 M a=0.85，C L=0.52展向载荷系数分布Fig.9 The load coefficient distribution along the wing at M a=0.85，C L=0.52

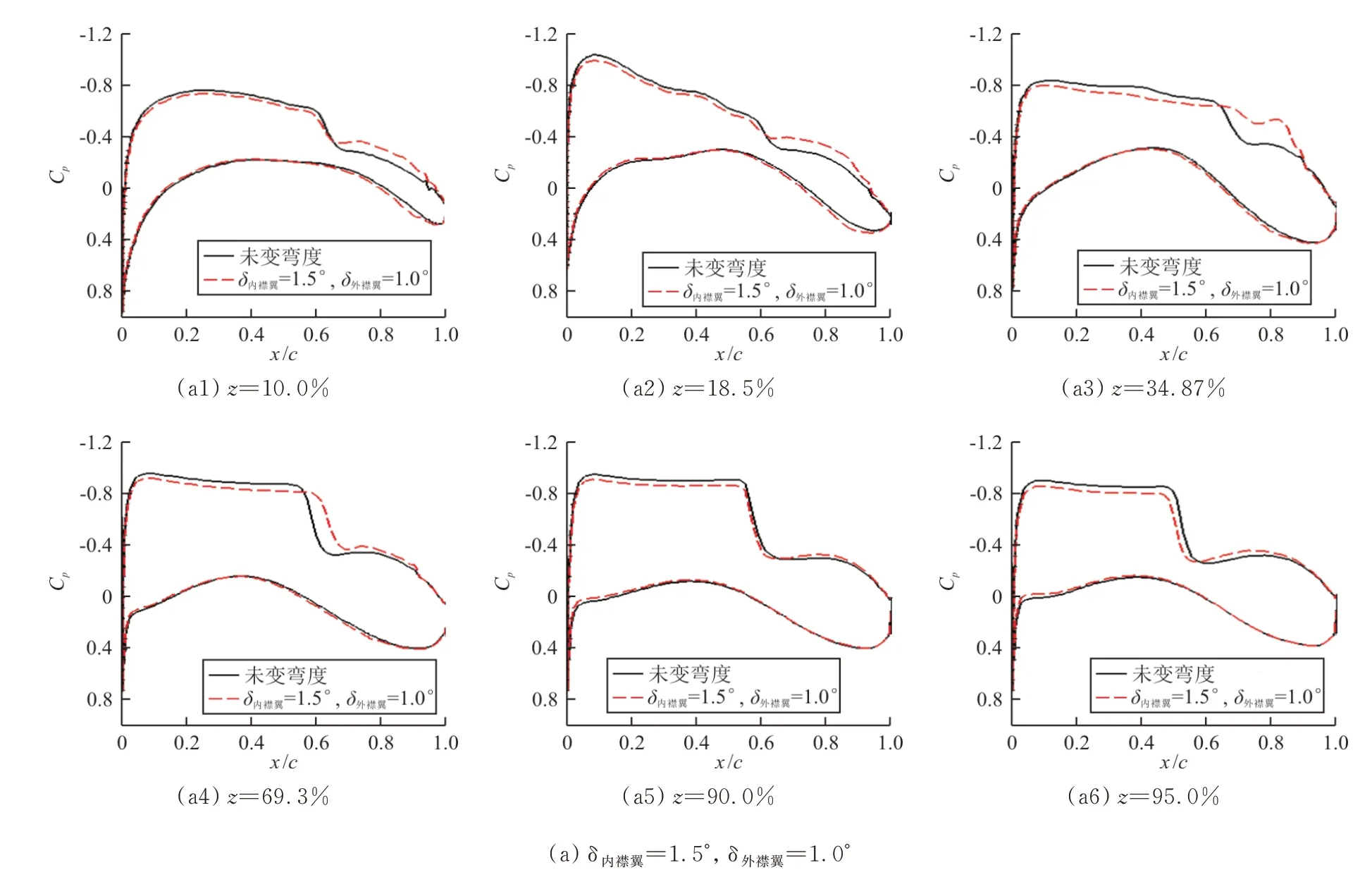
从图8～图9可以看出：后缘变弯度使内翼和中外翼区域的激波有所减弱，从而减小了波阻。

3.3 非设计点2：M a=0.85，C L=0.45

样本点全机配平构型与未变弯度全机配平构型阻力系数差量云图如图10所示，可以看出：在整个变化范围内，没有阻力降低的样本点。在基本样本点数值模拟结果基础上，［-0.5°，1°］范围内增加7个样本点，样本点中阻力系数最小点对应的内、外襟翼分别为-0.5°和0°，相比未变弯度状态，阻力系数增加0.05 cts。

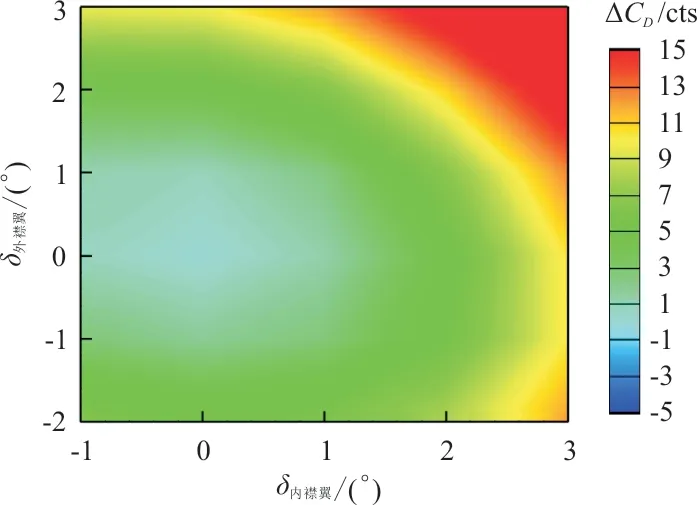
图10 非设计点2基本样本点全机配平构型阻力系数差量云图Fig.10 The drag dispersion contour at off-design point 2

该状态的展向压力分布如图11所示，以36个样本点建立2阶响应面模型，以全机配平构型阻力最小为优化目标对内、外襟翼偏角进行优化。优化后内、外襟翼偏角分别为-0.15°和0.13°，相比未变弯度状态，配平后阻力系数降低0.07 cts。该状态的展向压力系数和载荷系数分布如图12所示。

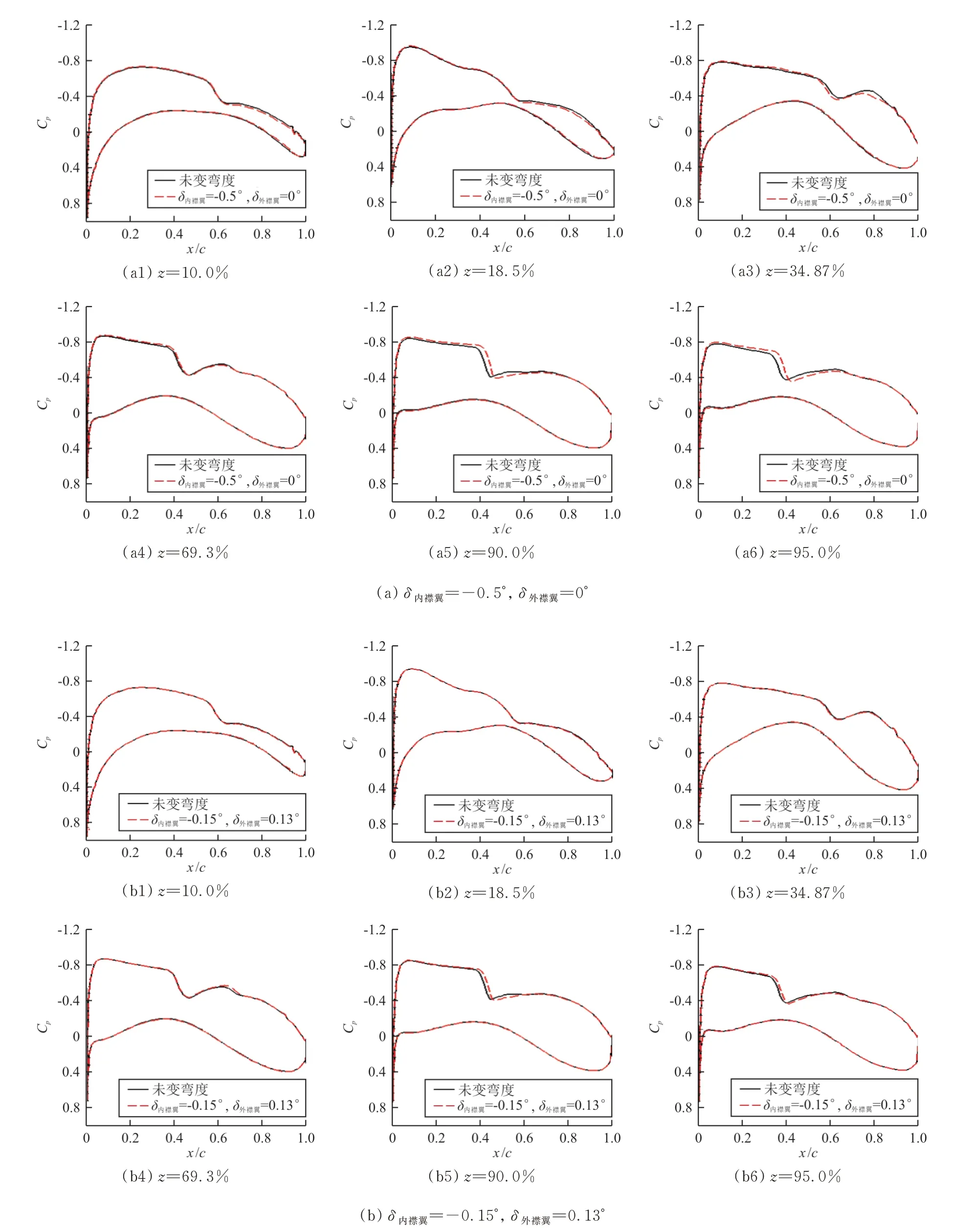
图11 M a=0.85，C L=0.45展向截面压力分布Fig.11 The sectional pressure distribution along the wing at M a=0.85，C L=0.45

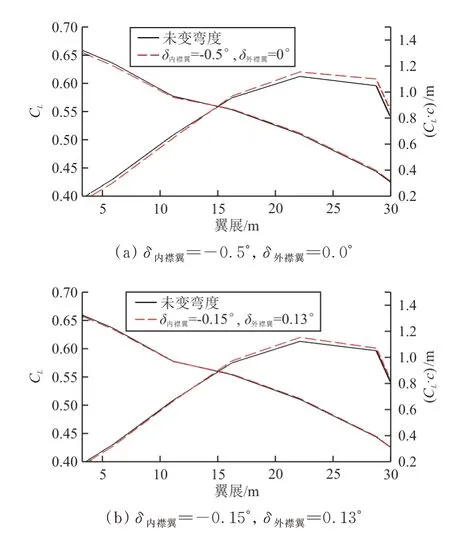
图12 M a=0.85，C L=0.45展向载荷系数分布Fig.12 The load coefficient distribution along the wing at M a=0.85，C L=0.45

从图12可以看出：在该状态下变弯度基本无法获得减阻收益。

3.4 非设计点3：M a=0.80，C L=0.48

基本样本点全机配平构型与未变弯度全机配平构型阻力系数差量云图如图13所示，可以看出：在内襟翼［-1°，1°］、外襟翼［0°，2°］范围内，阻力系数差量为负值，具有减阻潜力。

图13 非设计点3基本样本点全机配平构型阻力差量云图Fig.13 The drag dispersion contour at off-design point 3

在基本样本点数值模拟结果基础上在［0°，1°］范围内增加4个样本点。样本点中阻力最小点对应的内、外襟翼分别为0°和1.0°，相比未变弯度状态，阻力系数降低0.83 cts。以33个样本点建立2阶响应面模型，以全机配平构型阻力最小为优化目标，对内、外襟翼偏角进行优化。优化的内、外襟翼偏角分别为0.28°和1.28°，相比未变弯度状态，配平后阻力系数降低0.92 cts。样本点最优阻力系数与优化结果同样相差不到0.1 cts。

样本最优阻力点与优化结果的展向压力系数分布如图14所示，样本最优阻力点与优化结果的载荷系数分布如图15所示。

图14 M a=0.80，C L=0.48展向截面压力系数分布Fig.14 The sectional pressure coefficient distribution along the wing at M a=0.80，C L=0.48

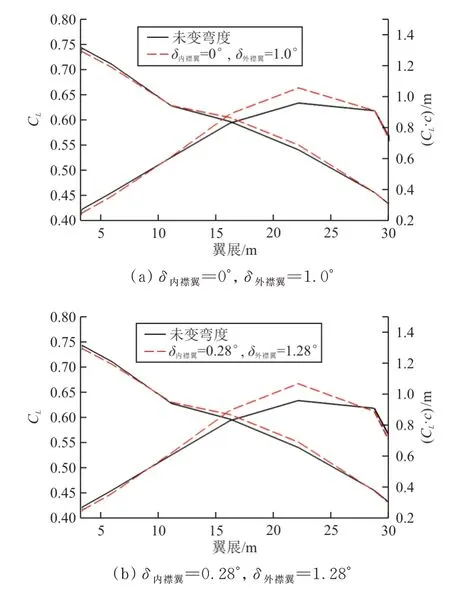
图15 M a=0.80，C L=0.48展向载荷系数分布Fig.15 The load coefficient distribution along the wing at M a=0.80，C L=0.48

从图14～图15可以看出：该状态激波位于机翼前缘区域，后缘变弯度基本没有对激波形态与强度产生影响；后缘下偏抑制了该飞行状态下的过配平现象，阻力降低主要来自配平阻力以及诱导阻力的降低。

4 变弯度操作需求及综合减阻分析

根据优化设计结果，基于工程约束考虑的最优样本点与优化结果的减阻量基本相当。在巡航马赫数，除小升力系数情况，后缘变弯度均能带来减阻收益；在=0.8，后缘变弯度也能带来减阻收益。每一个状态所对应的襟翼偏角均不同。本节对实际飞行中进行变弯度操作次数的需求进行分析。根据=0.85，C 为0.48、0.52两个状态的变弯度优化结果，对内/外襟翼偏转分别为0.5°/0.5°以及1.5°/1°时的全机配平构型升阻特性进行数值模拟。

=0.85未变弯度与两次变弯度操作后升阻比随升力系数变化比较如图16所示，可以看出：当C ≤0.46时，变弯度无法获得减阻收益，应保持原有巡航构型飞行，为保持高升阻比特性，飞机需增加巡航高度；当C ＞0.46时，采用巡航设计点的变弯度设置可实现减阻，获得比增加巡航高度更多的减阻收益；当C =0.50时，对于内/外襟翼0.5°/0.5°以及1.5°/1°的两个变弯度设置，配平后阻力特性几乎无差异，均可减阻1.7 cts；当C ＞0.50时，后者变弯度减阻效果优于前者。故在=0.85时，采用两种变弯度设置即可在C 为0.48～0.55范围内获得较大减阻收益，C =0.55时可使阻力系数降低6.7 cts，C =0.50可作为两个变弯度设置的过渡点。传统民用客机通常通过阶梯巡航使飞机保持在设计状态飞行，变弯度机翼能够在一定升力系数范围（C 为0.48～0.55）内实现与未变弯度机翼巡航设计点相当甚至更优的升阻比特性，因此可以获得比传统民用客机阶梯巡航更多的减阻收益。

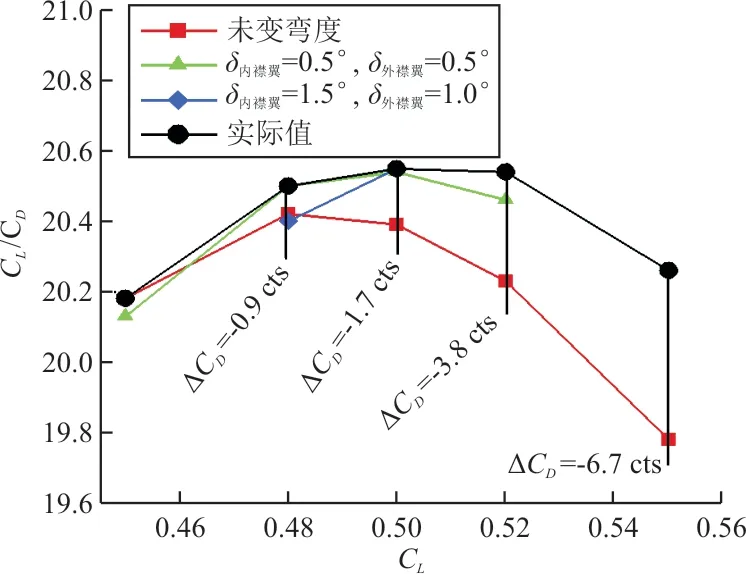
图16 M a=0.85未变弯度与两次变弯度操作的阻力特性Fig.16 The drag reduction of two camber setting at Ma=0.85

为0.80、0.83以及0.85时内、外襟翼分别下偏0.5°，全机配平构型的升阻比变化如图17所示。

图17 不同马赫数下变弯度全机配平构型减阻特性内襟翼0.5°，外襟翼0.5°Fig.17 The drag reduction of trimmed configuration at different mach number，δ内襟翼=0.5°，δ外襟翼=0.5°

从图17可以看出：该变弯度设置在较低马赫数时仍可实现减阻，在=0.8时，该变弯度设置减阻量比最优减阻量低0.3 cts，但由于该状态飞行时间较短，增加一次变弯度操作的收益可以忽略不计。

为了评估机翼变弯度后全航段综合巡航效率收益，分别研究定高巡航和一次阶梯巡航两种情况。定高巡航高度为10 km，对应升力系数变化范围为0.40～0.56，一次阶梯巡航的飞行高度分别为8和10 km，对应的升力系数范围为0.47～0.55。巡航燃油消耗率0.53 kg/h/kgf，对图16中实际升阻比曲线进行拟合获得上述升力范围内对应的升阻比以及阻力系数。采用布雷盖公式计算不同升力系数下的航时、航程，定高度、阶梯巡航不同升力系数阶段减阻量、航时和航程增量以及整个航段的综合减阻量、航时和航程增量如表2～表3所示。

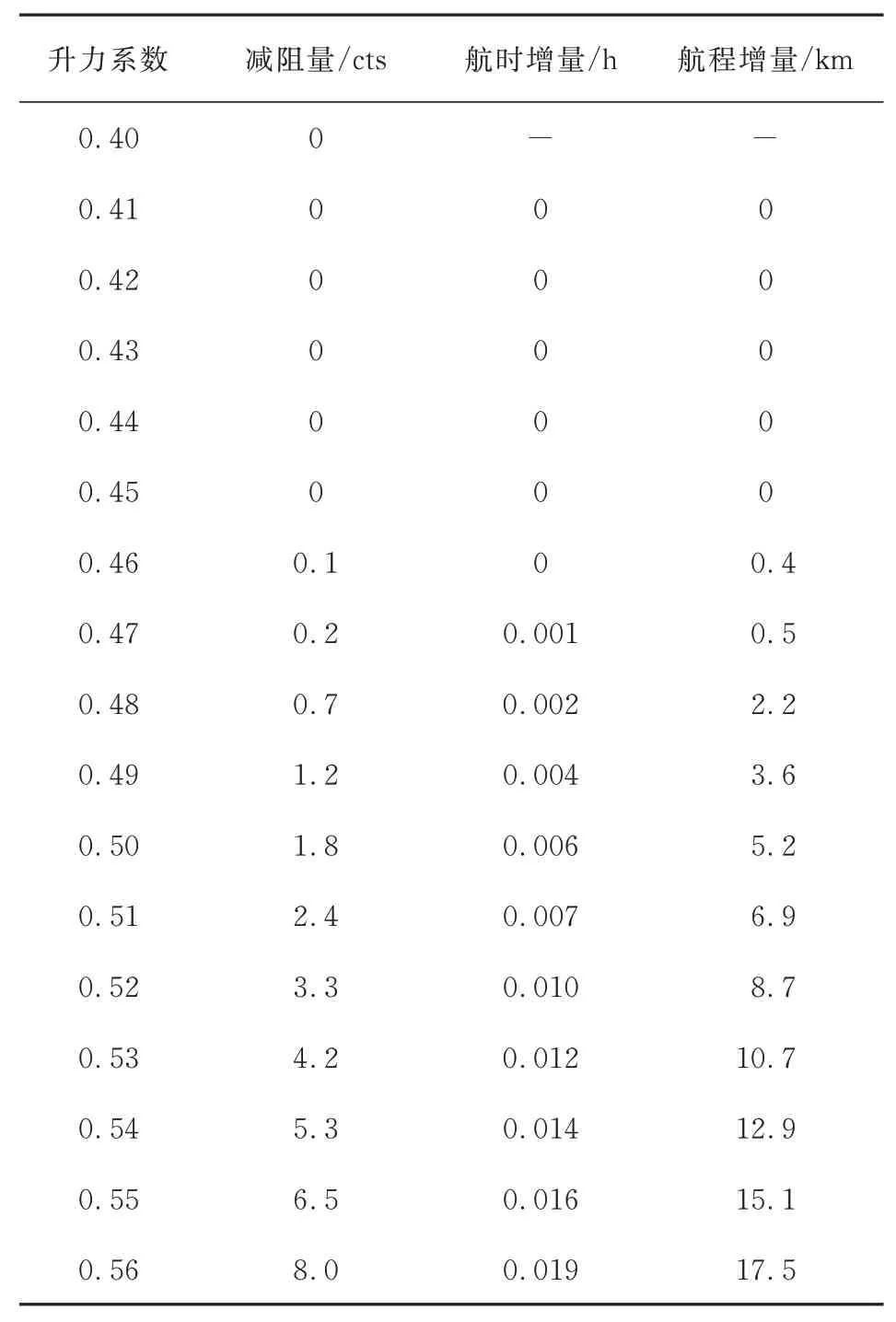
表2 定高综合巡航效率收益评估Table 2 General estimation of cruise efficiency at fixed altitude

表3 阶梯巡航综合效率收益评估Table 3 General estimation of cruise efficiency at stepped cruise altitude

从表2～表3可以看出：若在整个巡航阶段保持飞行高度不变，客机近一半时间都处于小升力状态，变弯度操作没有减阻收益，整个航段综合减阻只有1.9 cts，航时、航程提高0.72%；若进行一次阶梯巡航，本文的变弯度结果可在相应的升力范围内较好地实现变弯度减阻，整个航段综合减阻2.93 cts，航时、航程提高1.19%。

5 结 论

（1）采用以0.5°偏角为最小间隔的打靶法获得的最优阻力系数与所建立的代理模型优化结果减阻量差值小于0.1 cts，能够满足考虑工程约束的优化设计需求。

（2）在巡航马赫数，除小升力系数情况，后缘变弯度均能带来减阻收益；在较低马赫数（=0.8），后缘变弯度也能带来减阻收益。每一个状态所对应的襟翼偏角均不同。

（3）在=0.85时，采用两种变弯度设置即可在升力系数为0.48～0.55范围内获得减阻收益，变弯度机翼能够在一定升力系数范围内保持与巡航设计点相当甚至更优的升阻比特性，并且优于传统阶梯巡航所获得的收益。在较低马赫数（=0.8）时，采用巡航设计点的变弯度设置仍可实现减阻。