考虑低空运行环境求解无人机任务分配问题的研究

李松锐，张明，王蒙蒙，张进，李伯权

（南京航空航天大学民航学院，南京 211106）

0 引 言

在地震等自然灾害发生之后，需要及时对灾情进行探测，无人机能够利用红外探测仪，通过感知温度的差异来探寻目标，可以探测到人体的身体热量，从而知晓哪里还存在生命迹象，以便拯救更多的受灾群众。“黄金72小时”是地质灾害发生后的黄金救援期，在此期间内，人的存活率极高，因而在这个期间内需要紧抓时间，开展搜救工作，但是在发生灾害的地区，所提供的电力等能源以及飞行器的架数都比较有限，通航直升机和无人机搜索是搜救中的关键一环，是目前公认的有效手段也是当下研究的热点，救援部门都以最小化飞行路径的长度为目标，采用建模方法进行飞行器的路径规划。进行无人机任务分配方法主要有三种，分别是集中式、分布式以及分层级分布式分配。

集中式分配主要针对的是多旅行商问题中的路径求解问题。K.Dorling等研究了无人机运输的车辆路线问题时以集中式任务分配为基础来求解分配后的无人机路线问题；C.Murray等考虑了最后1 mile（1 mile=1.609 344 km）的运输系统；Zhou Z等研究了当移动人群感应遇见无人机时，节能任务分配和路线规划；Han Q等研究了基于多智能体强化学习的多无人机目标分配与路径规划联合优化。集中式分配的优点是总能给出最优解，但是集中式分配也存在着问题规模较大时非常耗时等缺点。

分布式分配需要无人机可以进行独立计算、分析和决策，朱晓宇等提出基于一致性差分进化的分布式任务分配；Zhou C等提出了一种在线随机激励机制，用于在实际众包系统中并行分配延迟容忍任务；Yu D等提出了运行时平衡聚类算法和依赖关系的平衡聚类算法。分布式分配的优点是在应用中无人机能在编队内通信，但是也要求无人机需要进行独立计算和决策，灵活性要求高。

分层级分布式分配，集集中式分配方式和分布式分配方式的优点于一身，Hua M L等提出利用车辆来运载和发射无人机的方案；Hu Xiaoxuan等研究了多个协作无人机团队的任务分配的分层方法；Yu Jianqiao等通过全面建模解决了考虑不同情况的多重UAV任务分配问题；Meng Wei等考虑了将多无人机的分散控制用于自主起飞，搜索和跟踪的问题；Ma Yunhong等提出了一种遗传和聚类算法相结合的协同优化算法；Wei Minghan等研究了能源约束下的覆盖路径规划；林林等设计了一种基于时间窗的无人机任务分配方法，利用冲突消解机制防止无人机出现资源死锁的情况。分层级分布式分配灵活性大，减少了计算时间。

综上所述，运用集中式任务分配方法或分布式分配方法各有优点和缺点，采用分层级分布式分配方法使得任务分配能发挥二者的优势，任务分配效果更佳。本文在分层级分布式分配方法的基础上建立多目标多无人机任务分配模型，在约束上考虑地形绕飞、低空风速对无人机续航能力的影响，在求解方法上考虑利用改进的遗传算法进行求解，并在求解中加入对立学习的方法增加解的多样性，得出分配结论。

1 考虑无人机性能及运行环境的任务分配模型

1.1 模型假设

（1）无人机的目标搜索点及释放位置的具体坐标已知，各节点之间的距离按照欧氏距离进行计算。

（2）每架无人机可以搜索多个目标点，每个目标搜救点只需要一架无人机进行搜索，但无人机的能耗不超过无人机的满电电量。

（3）将考虑低空风对无人机电池能耗影响、避障影响以及悬停影响下的能耗换算成无人机在不考虑以上因素匀速飞行状态时（如本文算例中机型A的速度为15 m/s）对应的航程进行计量。

（4）目标搜索点的探测时间根据灾情等级进行确定。

（5）各节点出发的UAV的速度均一致，无人机的航程成本与无人机完成任务换算成的航程成正比。

（6）不考虑无人机充电即多次循环使用问题，发射前为满电量。

1.2 变量说明

无人机任务分配模型的相关变量说明如表1所示。

表1 任务分配变量表Table 1 Task allocation variable table

1.3 目标函数

目标函数不仅要考虑无人机搜救产生的费用，还要综合考虑无人机的使用数量、总的完成任务最短时间即无人机任务的均衡合理性等因素。

首先，目标函数要使得总的费用最小，包括无人机飞行产生的费用和悬停产生的费用。则该项目标函数表达式如式（1）所示。

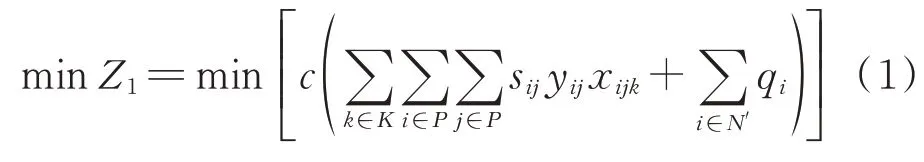
其次，无人机的实际数量有限，因而要尽量减少无人机的使用数量，得到第二项目标函数（其中0节点表示通航直升机释放无人机的位置）如式（2）所示。

最后，无人机完成其所分配的搜救任务的总能耗最小虽然会使得总的费用有所降低，但是在救援过程中，完成任务的时间也值得考虑，仅考虑费用问题可能会使得每架无人机完成任务的时间差别很大从而使得整体完成任务的时间较长，因而还需要在考虑费用的同时也要考虑各无人机完成任务耗时的最大时差降到最低，如式（3）所示。

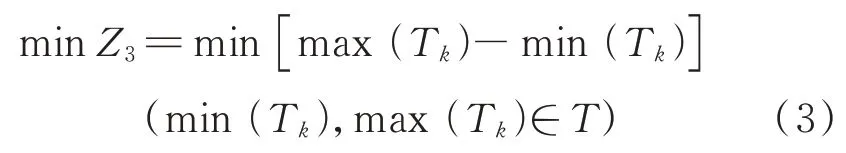
1.4 模型约束

模型的约束如下：

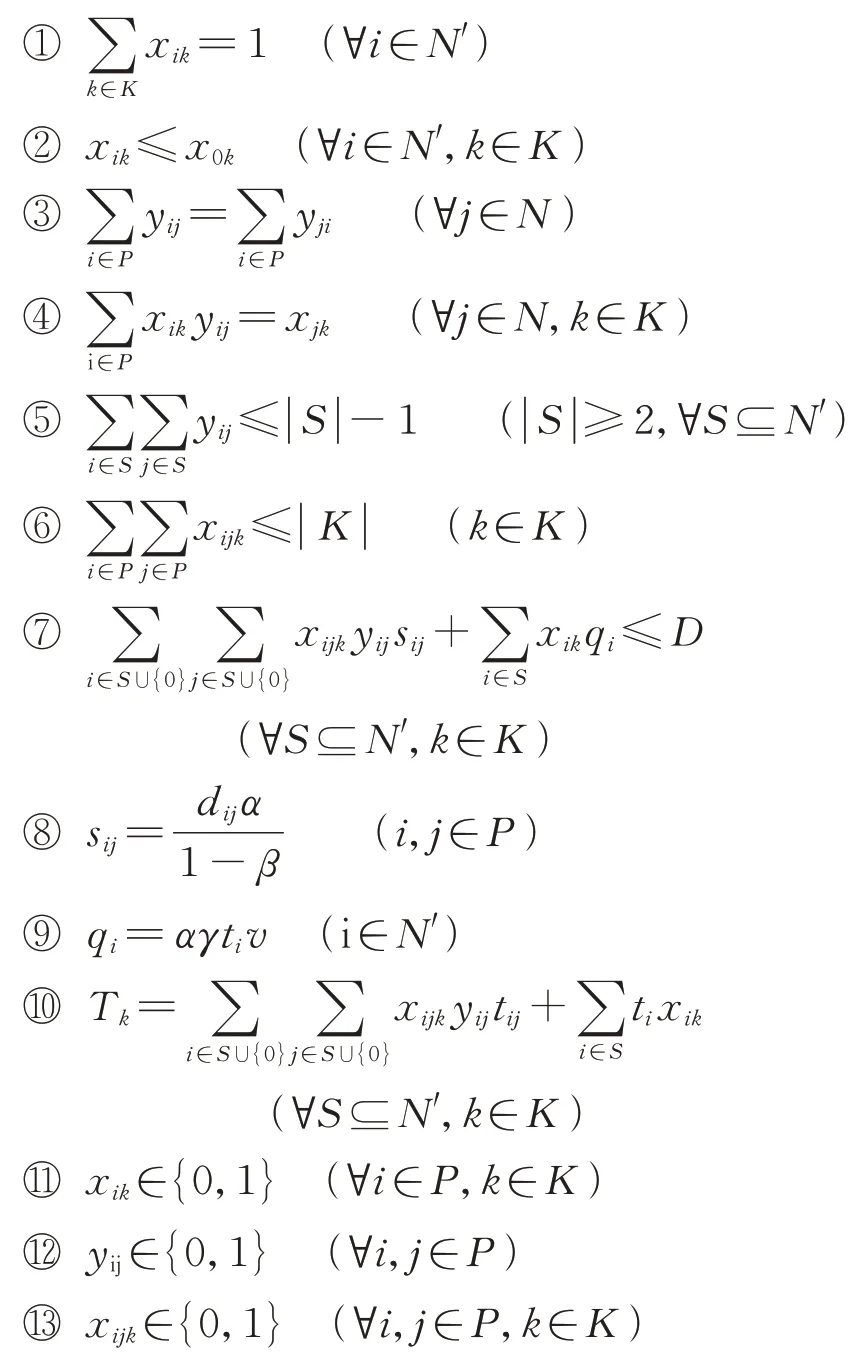
式（1）为目标函数Ⅰ，使总旅行成本最小化，包括在飞行中和悬停产生的成本。

式（2）为目标函数Ⅱ，考虑了无人机使用数量最少，使得购置无人机的成本以及养护成本减少。

式（3）为目标函数Ⅲ，考虑了任务的均衡性，使得总的完成任务的时间最短。

约束条件①确保每个搜索点只能由一架UAV进行搜索。

约束条件②表示如果无人机对搜救点进行搜索，则必须经过通航直升机释放无人机的位置点；如果无人机未经过通航直升机释放位置，则不会搜索任何搜救点。

约束条件③确保每条路线的连续性，即：访问节点的无人机必须离开节点。

约束条件④指出，如果存在从节点到节点的UAV飞行，则它们将由同一架UAV搜索。

约束条件⑤是经典子回路消除约束。

约束条件⑥是无人机的架数限制。

约束条件⑦表示无人机的电量限制为最大航程限制，即在考虑风和避障条件下将无人机飞行消耗的电量和悬停消耗的电量之和，换算为理想状态下匀速飞行的航程进行计算，不得大于无人机的最大航程。

约束条件⑧～约束条件⑨定义了航程的换算公式，为低空风对电池能耗影响系数、为无人机能耗预留系数、无人机飞行与悬停能耗比。

约束条件⑩定义了第架UAV完成分配给它的任务花费的总时间。

约束条件⑪～约束条件⑬定义了变量的取值范围。

2 NSGA-Ⅱ算法求解无人机任务分配

本文基于（Nondominated Sorting Genetic Algorithm-Ⅱ，简称NSGA-Ⅱ算法），采用快速非支配排序算法，引进精英策略和采用拥挤度及拥挤度比较算子，使得NSGA-Ⅱ运行速度快，求得的解的收敛性好。该算法求解UAV任务分配问题依赖于其进化机制。

2.1 双染色体编码方式

运用一种双染色体编码方式，双染色体均由整数编码，第一个染色体（染色体Ⅰ）代表靶序列，第二个（染色体Ⅱ）代表目标序列在染色体Ⅰ上的切割位置。在染色体Ⅰ上，每个基因都代表一个搜索目标的索引，在染色体Ⅱ中，任何基因的值都不得小于其前面的基因值。以四架UAV，10个搜救点为例进行编码。

例1：染色体Ⅰ（3，8，5，1，4，2，6，10，9，7），染色体Ⅱ（2，5，8）。

基因编码方式如表2所示。

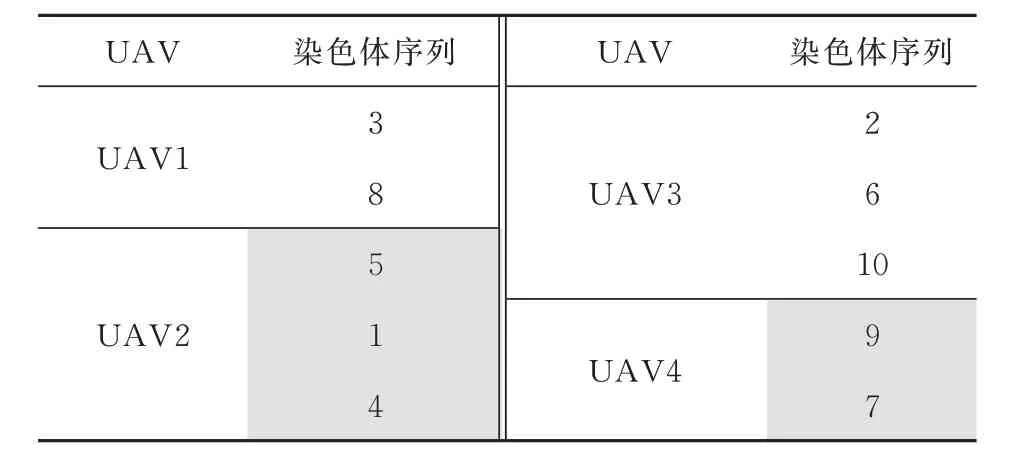
表2 例1染色体编码图Table 2 Chromosome coding of example 1

从表2可以看出：染色体Ⅱ是（2，5，8），因此染色体Ⅰ中的基因（3，8，5，1，4，2，6，10，9，7）在切割后分为四个子序列。四个子序列（3，8），（5，1，4），（2，6，10）和（9，7）分别代表UAV1、UAV2、UAV3和UAV4的目标序列。

2.2 基于对立的学习策略

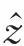
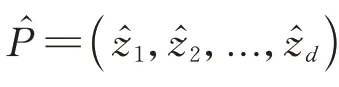
在无人机任务分配中，一个染色体Ⅰ是被视为计算对立面的多维点。

2.3 种群初始化

染色体Ⅰ上的基因总数为（搜救点的总数），染色体Ⅱ（切割位置）上的基因数目为(-1)，即无人机总架数减一。根据所建立无人机任务分配模型中的约束条件以及本文提出的编码方式，随机产生一定数量满足约束条件的个体即满足每架无人机电池容量约束，完成种群的初始化，产生初始种群数量为，通过对立学习的方式扩充种群数量为2，得到初始种群。

2.4 快速非支配排序

本文对于第代种群P 中每个个体，首先对基因进行解码得到无人机任务分配结果，根据式（1）～式（3）计算其对应的三个目标函数值，依据各目标函数值，对于每个个体都会得到两个参数n 和s （n 为在种群中支配个体的解的数量，s 为被个体所支配的解的集合），从而进行分层和排序，进而得到不同等级的帕累托前沿。不断地重复上述操作，直到所有个体都设置为前沿。

2.5 拥挤度比较算子

个体的拥挤度距离()计算公式如式（6）所示。

经过快速非支配排序之后，种群中的每个个体都具有非支配排序得到的非支配序列和拥挤度i 两个属性，根据这两个属性设定拥挤度比较算子，对于个体和个体，满足以下任意一个条件，则获胜。

（1）个体所在非支配层优于个体所在非支配层，有＜。

（2）和具有相同等级，同时个体的拥挤距离较大，即=且i =j 。

2.6 选择和精英保留

种群初始化以及每次迭代得到新的种群后，运用二元竞标法选择合适的父本进行交叉和变异操作。交叉和变异之后再对种群进行对立学习，扩充种群的规模。

2.7 交叉

本文只将交叉算子应用于染色体Ⅰ，而染色体Ⅱ在交叉过程中保持不变。这项工作使用了部分映射交叉运算符，其中一个亲本基因的一部分与另一亲本基因的一部分进行交换，其余基因则通过作图进行复制或再生。

2.8 多重变异

对于染色体Ⅰ，变异总共有四种操作方式，即保持、翻转、交换和滑动，一次可以产生四个后代。

3 算例分析

3.1 数据获取

无人机任务分配算例选取获取到的释放位置进行分析，该位置负责13个搜索点。

3.2 求解过程和结果分析

（1）种群初始化

首先需要进行种群的初始化，由于要满足电池容量约束，为计算简便，设置初始解为“一机一点”，即每架无人机搜索一个搜救点，总共有13个搜索点，则初始解使用了13架无人机，染色体Ⅱ编码为［1 2 3 4 5 6 7 8 9 10 11 12 13］。染色体Ⅰ通过随机的方式产生初始种群。

（2）参数设置

求解参数设置如表3所示。

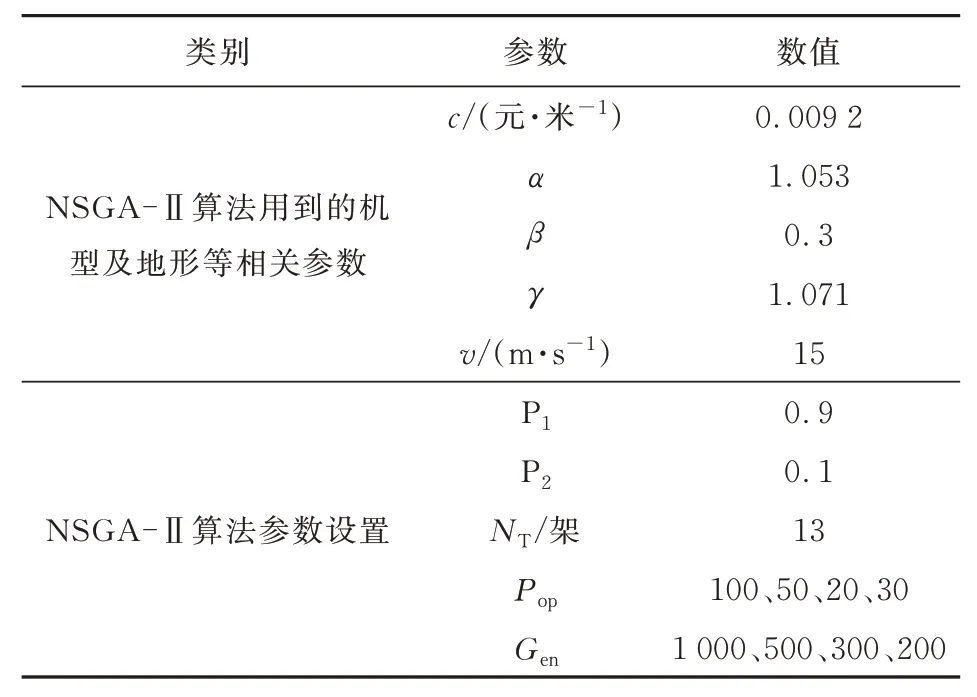
表3 求解参数设置表Table 3 Solving parameter setting table

（3）求解结果及分析

在正式求解前首先利用NSGA-Ⅱ和PSO算法以费用最小为目标函数进行求解，如图1所示，可以看出：NSGA-Ⅱ算法相比较于PSO算法求解任务分配的问题具有收敛速度快，并且得到的结果更优，求得的费用减少了2.08%。

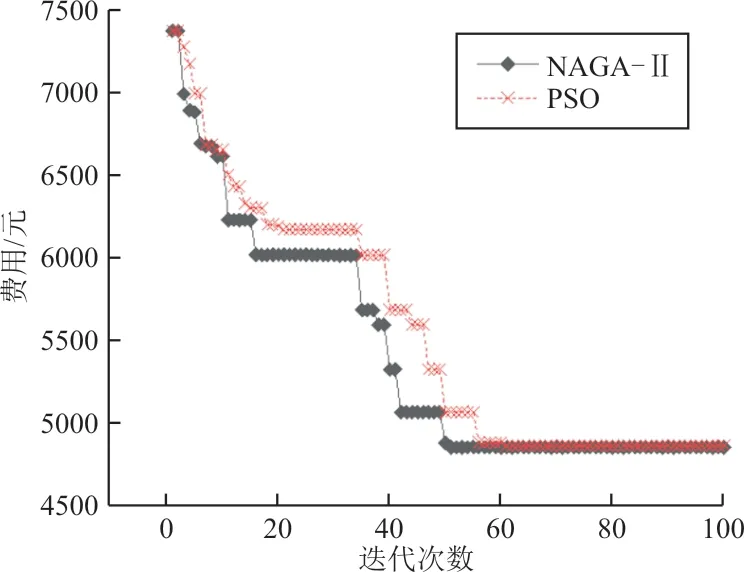
图1 NSGA-Ⅱ和其他算法迭代对比图Fig.1 Iterative comparison diagram of NSGA-Ⅱand other algorithms

分别设置种群规模=30，迭代次数为1 000、500、300、200，和=1 000，为100、50、30、20进行8次实验得到帕累托解，如图2～图3所示，蓝、品红、黄、黑色圆点分别表示在=30，=1 000、500、300、200下得到的帕累托解，在图3中，红、绿、蓝、青色圆点分别表示在=1 000，=100、50、30、20下得到的帕累托解。可以看出：当种群规模为30，迭代次数为1 000时能得到较多的帕累托解。取两个帕累托解以及遗传算法求解单目标的两组迭代得到的解，结果对比如表4所示，其中单目标模型求解后只能得到目标，即搜救的费用，为了便于比较，将其对应使用的无人机架数即，以及无人机执行任务时间极差求出。

图2 P op=30，G en为1 000、500、300、200得到的帕累托前沿Fig.2 The petro frontier obtained by P op=30 and G en=1 000、500、300、200

图3 G en=1 000，P op为100、50、20、30得到的帕累托前沿Fig.3 The petro frontier obtained with G en=1 000 and P op=100、50、20、30

表4 多目标模型与单目标模型结果对比Table 4 Comparison of results between multi-objective model and single-objective model

分析单目标求解得到的分配结果，显然与多目标模型得到的帕累托解相比，在使用的无人机数量上差别不大，单目标模型未考虑任务的均衡性，使得无人机之间的任务完成时间差别较大，但是在费用上具有明显优势。多目标求解的结果在费用上不具有优势，但是在完成任务的均衡性上具有明显优势。

而对于多目标求解结果，也可以根据实际需求获得需要的帕累托解。分别取侧重于搜救总费用最小、搜救无人机的数量最小和无人机任务差异性最小的结果进行灵敏度分析，无人机任务分配多目标模型的灵敏度分析侧重不同目标得到的结果如表5所示。

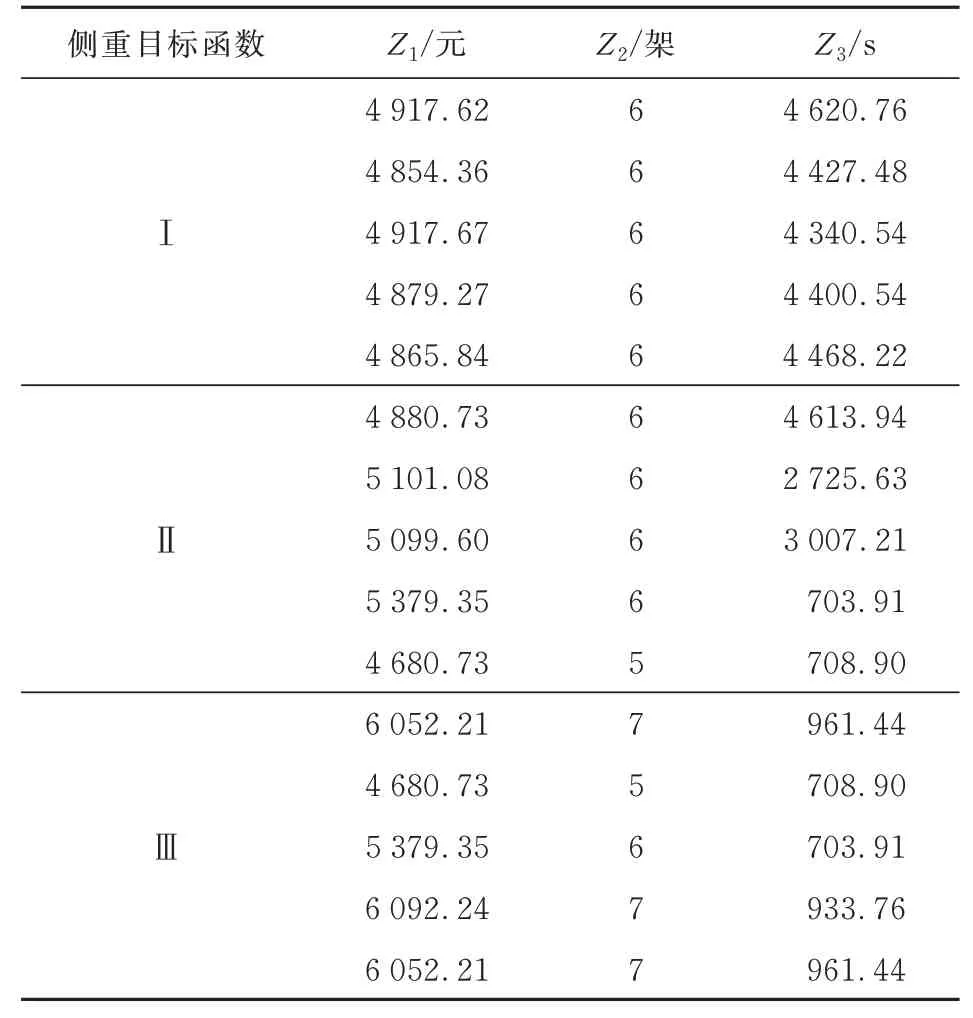
表5 多目标模型灵敏度分析侧重目标结果Table 5 Multi-target model sensitivity analysis focuses on target results

如果侧重的目标函数是Z (∈)并且={1，2，3}，则当Z 是侧重于目标时，Z (∈)可以表示为目标值矩阵，Z 为

如果Z (∈{})是侧重于Z 的目标值，φ 表示侧重Z 与侧重Z 的目标值变化率，则φ 可以表示为

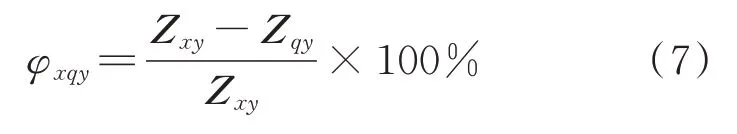
如果φ 为正，则目标趋势上升；否则，趋势是下降的。有关重点目标结果的比较分析，如表6所示。

表6 多目标模型中侧重目标结果对比分析（根据均值计算求得）Table 6 Focus on the comparative analysis of target results in the multi-target model（calculated according to the mean value）

从表6可以看出：当帕累托解侧重于搜救成本时，相比侧重于UAV数量和搜救时差最小，成本有所下降，且UAV任务最大时差都有大幅上升，其中相比侧重于UAV使用数量目标，成本目标的值下降不明显；当侧重于UAV使用数量时，相比侧重于另外两个目标函数，UAV使用数量有所下降，其中相比侧重于成本目标，UAV使用数量下降也不明显；当帕累托解侧重于UAV搜救最大时差最小时，相比侧重于另外两个目标函数，时差有所下降，且下降幅度特别大，另外两个目标函数的值却均有所上升。

在实际搜索救援中，需要综合平衡搜救时间、费用和无人机数量三个指标，使得搜救工作更加有效。一般更多是在考虑搜救均衡时间最少这个指标的基础上，带来成本和无人机数量的增加；但当实际搜救无人机的数量十分有限时，则需要加大时间或成本的投入；以经济利益为导向时，则会导致搜救时间的增加。

4 结 论

（1）在进行模型的求解计算时，利用了改进的NSGA-Ⅱ算法进行求解，相比较于PSO算法求解任务分配的问题具有收敛速度快的特点，并且得到的结果更优，费用减少了2.08%。

（2）通过算例得出考虑多目标的无人机任务分配模型的优异性，本模型可以根据搜救情况的现实需要，对于侧重于不同的目标，给出对应的分配方案。