基于Markov过程的卫星星座备份策略研究
骆天溯,赵灵峰,冯蕴雯,薛小锋,路成
(1.西北工业大学 航空学院,西安 710072)
(2.中科院微小卫星创新研究院通信卫星总体研究所,上海 201203)
0 引 言
备份卫星是星座正常运行的关键保障,对于维持星座性能有着十分重要的作用。若卫星星座中有卫星发生故障且未能及时更换,可能致使整个卫星星座瘫痪进而降低星座可用度。因此,有必要对低轨卫星星座备份策略进行研究,以保障星座中有卫星发生故障时能够获得及时更换,在保证星座可用度的前提下降低备份费用。
近年来,为了解决星座备份卫星数量优化问题,避免备份卫星过多造成备份成本过高和备份数量过少导致无法满足星座可用度指标的问题,国内外对星座备份策略进行了研究并取得了一定的成果。Wang Qinghua等研究表明,对于BDS系统增加MEO卫星的备份数量可大幅提高星座系统鲁棒性;T.J.Lang等、J.L.Palmade等对各国的导航卫星星座备份策略进行了研究和建模;A.V.Sedelnikov等提出了一种可以让备份卫星在空间备份时保持轨道高度和正确姿态的方法。但上述研究未考虑不同数量的备份卫星对星座可用度造成的影响。
J.F.Ereau等提出了基于Petri网的星座备份模型;C.Kelley等使用Markov模型来评估卫星系统的生命周期成本,提出了综合考虑采购、补给和运营成本因素下的星座备份模型;B.R.Sumter通过有限空间Markov决策过程建立了一个卫星备份模型。上述研究在建立星座可用度计算模型时没有考虑随着时间的推移星座的持续运行导致性能的下降。
M.Dishon等提出了基于(,)库存模型的卫星备份策略;P.Jakob等提出了一种基于(,)库存模型的同时考虑三种备份模式的两级可用度模型;赵立都等基于星座系统可靠度和备份卫星的可用性,分析了对备份卫星的轨道高度和轨道倾角的要求;胡敏等进行了基于Petri网的Walker导航星座备份策略研究,给出了在轨和地面同时备份情况下的星座可用度计算模型;王尔申等提出了基于Markov过程的GNSS星座备份策略,并评估了不同数量的备份卫星对星座可用度的影响;侯洪涛对GNSS系统进行了多层可用性分析并计算了考虑备份卫星时的星座可用性。上述研究没有考虑星座实际运行中的降级运行情况,使得星座可用性计算结果与工程实际存在差异。
为了解决以上问题,本文提出一种基于Markov过程的低轨星座备份策略,考虑星座中的故障卫星不能及时更换时降级运行,计算星座在使用不同备份策略下的可用度,并以某真实低轨星座为例,结合其在轨运行数据提出最优的备份策略。
1 问题描述与假设
星座可用性的概念具有很强的领域性和时代特点,根据具体的工程应用场景,本文中星座可用性的定义为星座提供额定服务时间所占的百分比。星座备份策略主要包括在轨备份、停泊轨道备份以及地面备份模式,其中,在轨备份的卫星与工作卫星处于同一轨道面上,备份卫星仅需通过简单的相位变换即可替换故障卫星;停泊轨道备份卫星处于比星座轨道更低的停泊轨道上,需通过轨道漂移以及变轨替换故障卫星;地面备份的卫星贮存在火箭发射基地或者卫星制造工厂中,通过按需发射替换故障卫星。对于卫星数量不多的星座而言,在轨备份模式替换时间短,星座可用度高,是一种最为常见的备份方式。各国均采用在轨备份方式对其全球导航星座进行备份,例如GPS、Galileo、GLONASS和北斗全球导航系统。本文在这一工程背景下开展基于Markov过程的低轨星座备份策略研究,该星座未采用备份卫星时的轨位如图1所示。

图1 无备份卫星的低轨星座布局示意图(策略0)Fig.1 Constellation layout of a LEO constellation without spare satellites(Strategy 0)
该星座由7条轨道组成,每条轨道上有3颗基础轨位卫星,由于在实际运行中没有考虑卫星备份,该星座可用度只有0.63,远低于指标要求,需要综合考虑备份费用和可用性要求,提出最优的星座备份策略。
为了简化建模过程,提高模型的工程适用性,对基于Markov过程的低轨星座备份模型合理地做出如下假设:
(1)假设卫星的寿命服从指数分布,即卫星全寿命周期故障率恒定。
(2)由于只考虑在轨备份模式,一旦基础轨位卫星发生失效故障,该轨道上的备份卫星能够立即替换该失效卫星,替换完成后认为星座的状态没有发生变化;如果失效的卫星没有被及时替换,星座的状态就会发生变化。
(3)卫星的任意一个部件失效都会导致整个卫星不能正常工作。
(4)所有基础轨位卫星与所有备份卫星构造相同,单星可用性相同。
2 单星可用度模型及求解
单颗卫星的Markov状态转移过程如图2所示。

图2 卫星Markov状态转移关系图Fig.2 Markov state transition process of a satellite
图2中,0状态表示卫星正常工作状态;1状态表示卫星故障状态;为卫星失效率,表示单位时间内卫星发生故障的概率;为卫星维修率,表示单位时间内卫星由故障状态转移成正常运行状态的概率。在失效卫星无备份卫星进行替换时,维修过程通过在轨服务方式实现;当有备份卫星进行替换时,维修过程通过备份卫星替换故障卫星实现。和的计算公式为

式中:为卫星的平均无故障间隔;为卫星的平均维修时间。
、与卫星运行时间、维修时间、失效次数有关,计算公式为

根据可用性理论,单星的稳态可用度计算模型为

3 星座可用度
3.1 星座可用度模型
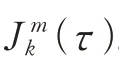
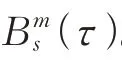
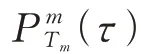



综上,共拥有条轨道的星座中第条轨道有T颗卫星正常工作的概率为
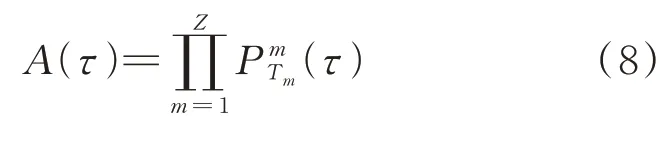
3.2 星座可用度模型求解方法
当初始时刻=时,基础轨位卫星星座的故障状态向量为

其中,

式中:A 为基础轨位卫星的单星可用度。
同理可得初始时刻=时备份卫星星座的故障状态向量为
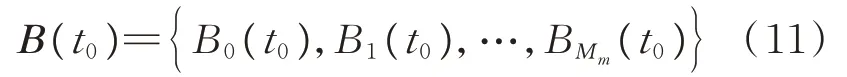
其中,

式中:A 为备份卫星的单星可用度。
当为任意正整数,Δ为状态转移时间间隔时,=+Δ时刻基础轨位卫星星座的故障状态向量为
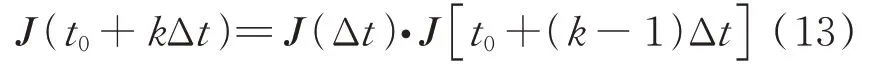
其中,


其中,
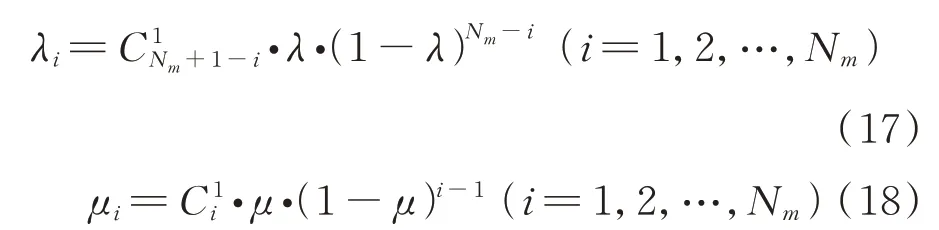
同理,在=+Δ时刻备份卫星星座构成的故障状态向量为

4 案例分析
以构型参数Walker 21/7/1:600 km,55°星座为例,考虑星座降级运行情况,将星座等级定义(定义中的卫星包括基础轨位卫星和备份卫星)如下:
(1):星座中全部21颗卫星正常运行,即每条轨道上至少有3颗卫星正常工作,此时星座可用度为;
(2):星座中至少有20颗卫星正常运行,此时星座可用度为;
(3):7个轨道平面上均至少有2颗卫星正常运行,此时星座可用度为;
(4):7个轨道平面上有一个轨道平面少于2颗卫星正常运行,此时认为星座不可用。
在不考虑备份卫星的情况下,该星座在运行过程中的运行时间和故障数据如表1~表2所示。星座使用方提出的运行要求为:星座运行等级要求为级,星座可用度不低于0.99。在此要求下求出使星座备份费用最低的星座备份策略。

表1 某低轨星座基础轨位卫星运行时间表Table 1 Operating schedule of baseline satellites of a LEO constellation
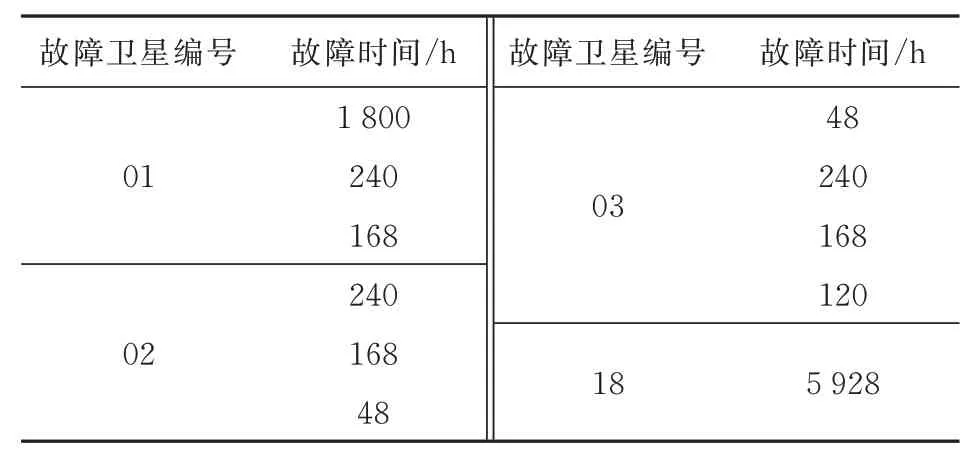
表2 某低轨星座基础轨位卫星故障数据表Table 2 Satellite failure data of baseline satellites of a LEO constellation
从表1~表2可以看出:卫星总运行时间为140 662 h,总故障时间为9 168 h,总故障次数为11次。
备份策略1中的星座由28颗卫星组成,其中01号~21号为21颗基础轨位卫星;22号~28号为7颗备份卫星。基础轨位卫星分布在A~G七条轨道上,每条轨道上有3颗基础轨位卫星;备份卫星分布在A~G轨道面上,每条轨道上有1颗备份卫星。备份策略1示意图如图3所示。

图3 星座备份策略1示意图Fig.3 Constellation spare strategy 1
备份策略2中的星座由35颗卫星组成,其中01号~21号为21颗基础轨位卫星;22号~35号为14颗备份卫星。基础轨位卫星分布在A~G七条轨道上,每条轨道上有3颗基础轨位卫星;备份卫星分布在A~G轨道面上,每条轨道上有2颗备份卫星。备份策略2示意图如图4所示。

图4 星座备份策略2示意图Fig.4 Constellation spare strategy 2
备份策略3中的星座由42颗卫星组成,其中01号~21号为21颗基础轨位卫星;22号~42号为21颗备份卫星。基础轨位卫星分布在A~G七条轨道上,每条轨道上有3颗基础轨位卫星;备份卫星分布在A~G轨道面上,每条轨道上有3颗备份卫星。备份策略3示意图如图5所示。

图5 星座备份策略3示意图Fig.5 Constellation spare strategy 3
通过星座运行时间(如表1所示)和卫星失效数据(如表2所示),使用式(5)可以求出单星平均可用性为0.978 7,再根据式(8)可以求出不同备份策略下不同星座等级的星座可用度,当Δ取1 h时,算法在300Δ后趋于稳定,使用第3节提出的模型以及求解方法分别对不同星座等级、不同备份策略下的星座可用度进行仿真,仿真结果如表3所示。
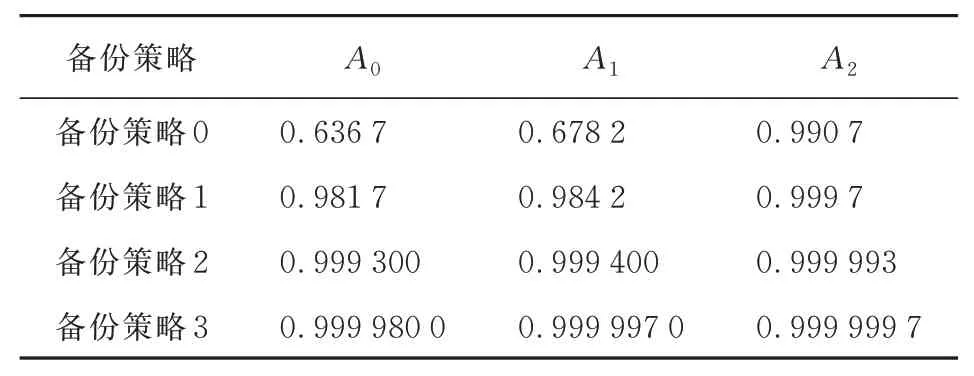
表3 不同备份策略和不同星座等级下星座可用度仿真结果Table 3 Simulation results of constellation availability under different spare strategies and different constellation levels
不同备份策略及不同星座等级对星座可用度的影响如图6所示。

图6 不同星座等级和不同备份策略对星座可用度的影响Fig.6 Impact of different constellation levels and different spare srategies on constellation availability
从图6可以看出:星座备份策略和星座等级对星座可用度都有很大的影响。备份卫星数量越多星座可用度越高,采用备份策略3时星座可用度几乎为1,然而备份费用也是三种策略中最高的;星座性能要求越高星座可用度越低,当星座性能要求达到等级时星座可用度最低,星座性能达到等级时,备份策略0、备份策略1和备份策略2的星座可用度增加明显;在星座性能为等级时,增加备份卫星数量会显著增加星座可用度;在可用度≥0.99的要求下,备份策略0和备份策略1的可用度未达到指标要求,备份策略3的可用度大于指标要求但备份费用过高。综合考虑可用度指标要求以及备份费用,备份策略2是最优选择。
5 结 论
(1)在星座等级为级、可用度指标为0.99的要求下,备份策略2为最优备份策略,即在每个轨道面上备份两颗卫星可以兼顾星座性能与经济效益;若不考虑经济效益则备份策略3可以达到最高的星座性能。
(2)对于备份策略0而言,星座等级从提升到带来的星座可用度提升十分明显;对于备份策略1、备份策略2和备份策略3而言,星座等级从提升到带来的星座可用度提升更加明显。

