冲击载荷下正弦波纹夹芯圆柱壳的轴向压缩和吸能特性

郝孝恒，张天辉，王根伟，沈文豪，闫 栋，沙风焕

（1. 太原理工大学材料强度与结构冲击山西省重点实验室, 山西 太原 030024；2. 太原理工大学机械与运载工程学院, 山西 太原 030024；3. 太原理工大学航空航天学院, 山西 晋中 030600）

金属薄壁结构因具有良好的吸能特性，广泛地应用在汽车、航空航天等领域。关于薄壁的吸能和变形特性已有大量研究工作。在薄壁圆柱壳研究中，Guillow 等[1]对具有不同长径比和高度的圆柱壳进行了准静态压缩实验，发现圆柱壳会产生不同模式的变形。朱文波等[2]研究了轴向冲击下薄壁圆柱壳的动态吸能特性，发现惯性对其吸能特性的影响不大，比吸能和平均压溃力随冲击速度的提高而增大。Jandaghi 等[3]通过改变圆柱壳的壁厚，形成了梯度圆柱壳，相较于普通圆柱壳，梯度壁厚更有利于塑性铰的产生，因而具有更优异的吸能特性。Sadighi 等[4]研究了具有轴向波纹的薄壁圆柱壳，实验和模拟结果表明波纹圆管能够提高压缩力效率和能量吸收。Yao 等[5]设计了一种多边形折纸圆柱壳，在轴向加载下，相较于传统圆柱壳，折纸圆柱壳的初始最大峰值力降低了56.96%。Zhu 等[6]探究了具有不同混合比的铝和碳纤维增强塑料构成的圆柱壳的压缩破碎行为，发现外部铝管和内部黏附碳纤维增强塑料能够改变圆柱壳的变形模式，具有良好的吸能性能。

在薄壁夹芯圆柱壳研究中，Hou 等[7]设计了一种新型三明治夹芯双圆柱壳，发现芯层和双圆柱壳能够有效地提高结构的吸能能力。而后，Wu 等[8]通过傅里叶级数展开法设计了一种新型的傅里叶变截面管，分析了具有不同傅里叶截面形状的薄壁圆柱壳在轴向冲击下的能量吸收特性，实验表明，结构的最大比吸能随着截面周长的增加而增大，最高增幅77.54%。随着数值模拟技术的进步和新型材料的涌现，Fu 等[9]发展了一种具有“X”形肋条的新型仿生竹筒结构，结果表明，在轴向压缩过程中该结构的耐撞性能得到提高。侯淑娟[10]针对轴向和横向载荷下的正方形薄壁构件，对多胞元构型的壁厚和截面宽度进行了抗撞性优化设计，发现四胞元构件具有良好的吸能特性。闫栋等[11]开展了类向日葵结构的瓣尖压和瓣间压两种径向冲击实验，发现瓣间压比瓣尖压的能量吸收最高提高44.6%。白江畔等[12]构建了多胞元薄壁结构模型，研究了不同冲击载荷下结构的动态压溃响应和比吸能，结果表明，结构的动态压溃行为受肋板夹角和冲击速度的影响较大。

目前结构的轻量化越发受到重视，在保持质量不变的情况下追求更优异的吸能效果，即结构的比吸能更高。正弦波纹结构的加工较简单，工程应用较广泛，然而针对正弦波纹夹芯圆柱壳在轴向载荷下的吸能特性研究仍有不足。为此，本研究将基于准静态轴向压缩实验，利用有限元方法对夹芯圆筒的力学行为和吸能特性进行数值分析，探究夹芯圆柱壳的变形模式，分析正弦波纹结构参数对压缩行为的影响，以期为夹芯吸能结构设计提供参考。

1 力学模型

1.1 几何模型

正弦波纹夹芯圆柱壳结构如图1 所示。正弦夹芯结构的壁厚为0.5 mm，高度为45 mm，截面的几何形状可表示为

图1 正弦波纹圆柱结构示意图Fig. 1 Schematic diagram of a sinusoidal corrugated cylinder

1.2 材料参数

试件材料选择Al 6061-O，为各向同性材料，密度ρ 为2.7 g/cm3，泊松比µ为0.3。根据国家标准GB/T 228.1—2010 测试了哑铃形拉伸试样在准静态（应变率为10-4s-1）拉伸下的力学参数，其应力-应变曲线如图3所示。

由图3 可知，初始屈服强度σ0=239.7 MPa，弹性模量E=68.6 GPa。模拟中，采用双线性弹塑性模型，试件无预加载，不考虑断裂和损伤。由于是准静态压缩实验，空气流动缓慢，因此不考虑夹芯圆柱壳中空气可压缩性和黏性对结构的影响。

图3 Al 6061-O 的工程应力-应变曲线Fig. 3 Engineering stress-strain curves of Al 6061-O

2 数值模型构建与验证

2.1 有限元模型构建

在ABAQUS 中建立正弦波纹夹芯圆柱壳的有限元模型，其压缩示意图如图4 所示，其中上、下板为刚体，夹芯圆柱壳放置在上、下板之间，下板设为固定约束。正弦波纹结构和双圆柱壳均采用S4R 壳单元，这是因为S4R 的适应性良好，既可以用于厚壳模拟，又可以用于薄壳模拟，而且采用减缩积分，容许有限薄膜应变。夹芯圆柱壳的轴向压缩问题采用显式求解器。在压缩过程中，固定下板，上板以恒定速度v向下压缩，上板、下板和正弦夹芯双圆柱壳使用自接触，发生接触时，能够有效地模拟多面接触问题。

图4 正弦波纹圆柱壳结构的有限元模型Fig. 4 Finite element model of sinusoidal corrugated cylindrical shells

2.2 模型验证

本研究中的试件采用电火花线切割制成，试件的直径D=45 mm，高度h=45 mm，双圆柱壳及正弦波纹夹芯的壁厚均为0.5 mm。通过计算机控制万能材料试验机对A15N8 进行准静态压缩实验，压头以2 mm/min 的速度压缩，直至结构达到密实化。通过压头的力传感器采集载荷信号，压缩载荷-位移曲线如图5所示。

通过上板以1 m/s 的恒定压缩速度模拟准静态压缩过程。图5 给出了数值模拟得到的压缩载荷-位移曲线，与实验结果吻合较好。模拟与实验得到的峰值压力分别为45.91 和47.19 kN，相对误差为-2.71%。当压缩量为32 mm 时，模拟与实验得到的能量吸收分别为804.12 和814.61 J，相对误差为1.28%。

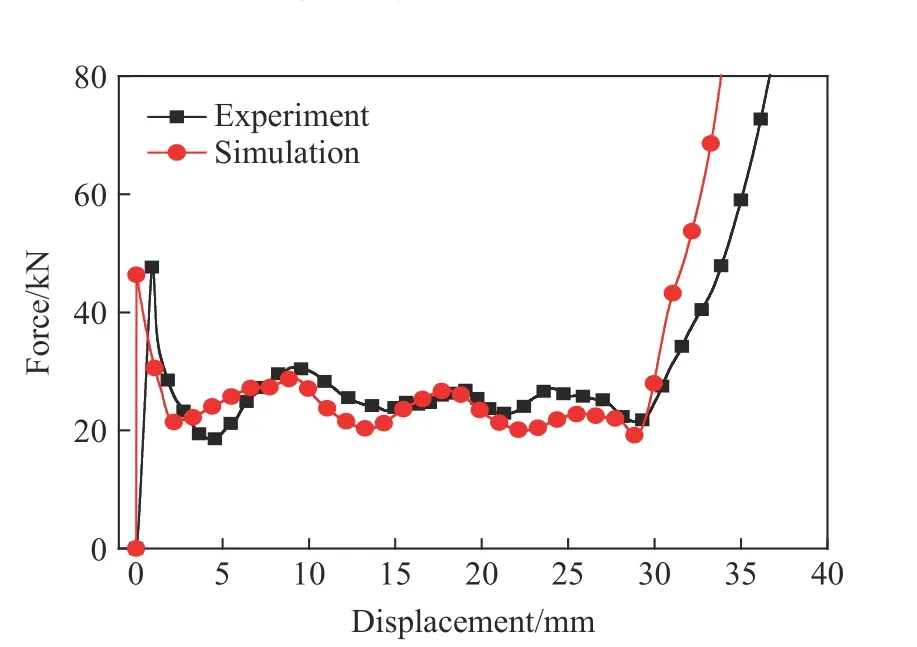
图5 压缩载荷-位移曲线的模拟与实验结果对比Fig. 5 Comparison of compressive force-displacement curves between simulation and experiment

对结构进行有限元网格敏感性分析，采用0.5、0.8、1.0 mm 3 种不同网格尺寸对A15N8 进行网格划分，并进行压缩速度为1 m/s 的数值模拟，所得载荷-位移曲线如图6 所示。可以看到，3 种网格尺寸下压缩载荷随位移的变化趋势基本一致。综合考虑计算精度和计算效率，在后续数值模拟中网格尺寸选用1.0 mm。图7 给出了在1 m/s 的压缩速度下A15N8 夹芯结构的动能和应变能的对比结果。在整个压缩过程中，动能与应变能的比值小于5%，因此1 m/s 的速度可以用于模拟准静态加载过程[13]。

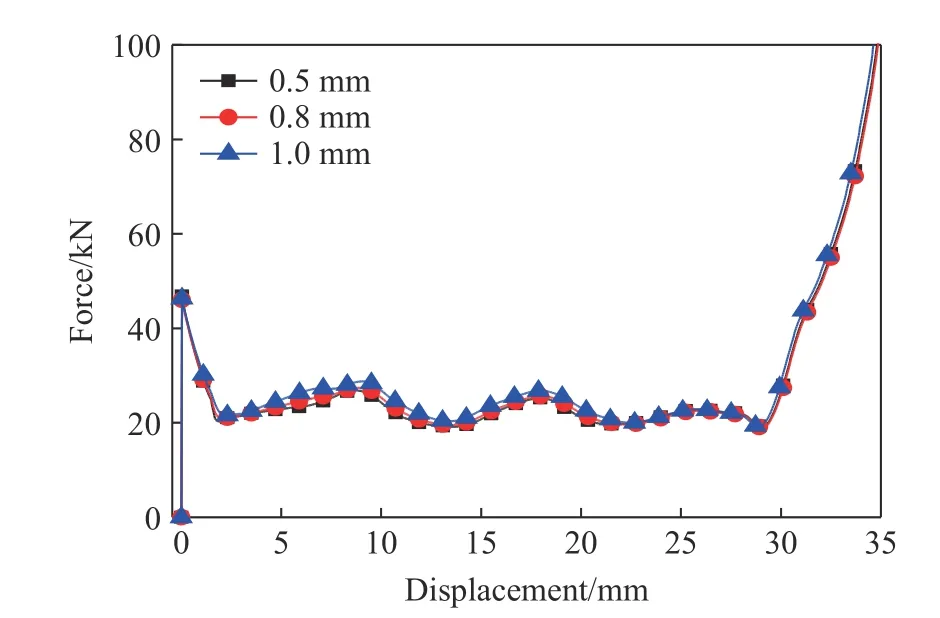
图6 网格敏感性分析Fig. 6 Mesh sensitivity analysis

图7 动能与应变能的对比Fig. 7 Comparison of kinetic energy and internal energy

3 参数分析

针对正弦波纹夹芯圆柱壳结构，以总能量吸收（energy absorption，EA）、平均压缩载荷（mean crushing force，MCF）、比吸能（specific energy absorption，SEA）、压缩力效率（crushing force efficiency，CFE）作为能量吸收指标进行吸能评估，表达式如下

Guillow 等[1]把不同高度、直径、壁厚的普通薄壁圆管的变形模式分为5 类：轴对称、非轴对称、混合、欧拉和其他，其中轴对称模式拥有最好的吸能特性。本研究中夹芯圆柱壳的长径比为1，只产生前3 种变形模式。在压缩过程中，结构产生渐进性折叠的层次褶皱，而且从俯视图可以看到内外壳和夹芯都是轴对称的，这是轴对称变形，如图8(a)所示（对应的结构为A15N12）。结构在初期产生渐进性折叠的层次褶皱，随后产生非轴对称褶皱，而且外壳和夹芯都近似轴对称，内壳是非对称的，这是非轴对称变形，如图8(b)所示（对应的结构为A15N8）。发生混合变形模式的结构在压缩过程中产生不规则的褶皱，外壳对称，夹芯和内壳不对称，如图8(c)所示（对应的结构为A15N4）。

图8 典型的轴对称、非轴对称和混合变形模式Fig. 8 Representative deformation of axisymmetric, non-axisymmetric and mixed modes

3.1 A 和N 对变形模式和吸能的影响

下面研究图2 所示的25 种正弦波纹夹芯圆柱壳在压缩量d=32 mm 时的能量吸收性能。所有结构的壁厚均取0.5 mm。图9 给出了不同A和N对应的正弦夹芯双圆柱壳的变形模式。可以看到：当N=12 时，不论A取何值，夹芯正弦波纹双圆柱壳均发生轴对称变形；当A≥7 mm 时，在A不变的情况下，随着N的增加，结构的变形模式从混合模式逐步转变为轴对称模式；而当A=3 mm 时，结构的变形模式则从非对称模式转变为轴对称模式，没有产生混合模式。

图2 不同A 和N 的夹芯圆柱壳Fig. 2 Sandwich cylindrical shells with different A and N

图9 不同的A 和N 下壳体的变形模式Fig. 9 Collapse modes of shells with various A and N

图10 给出了夹芯圆柱壳质量随A和N的变化趋势。可以看到，N增加时，结构的孔隙率变小，质量单调增加，因为圆柱壳的壁厚是均匀的，N越小，内壳的质量占比越大。当N=4 时，质量随着A的减小而增大；当N=6 时，质量随着A的减小先减小后略微增大；当N>6 时，质量随着A的减小而单调减小。

图10 不同的A 和N 下试件的质量Fig. 10 Mass of specimens with different A and N

如图11(a)所示，在A固定的情况下，随着N的增大，结构的EA 增加，变形模式由混合变形模式逐渐变为轴对称变形模式（见图9），这是由于变形模式逐渐变得稳定，从而导致EA 增加。然而，在当前追求轻质化的需求背景下，SEA 更加重要。如图11(b)所示，当A=19 mm 时，虽然结构的EA 随着N的增加而增大，但是此时夹芯圆柱壳质量（图10）也增加，而且夹芯圆柱壳质量对SEA 的影响更显著，导致SEA 随着N的增加而减小。从图11 可以看出：N相同时，随着A减小，EA 增大，除N=4 外，SEA 随着A的减小而增大，而且其增长速率快于EA 的变化率；当N=4 时，A减小时，质量增加，SEA 先略微增大后略微减小。当A=7, 3 时，夹芯圆柱壳质量的差距减小，除A7N10 和A7N12 外，SEA 呈明显上升趋势；当A≤7 时，N=10 和N=12 的截面形状接近，夹芯质量占比也非常接近，所以两者的SEA 非常接近。

图11 不同的A 和N 下夹芯圆柱壳能量吸收的模拟结果Fig. 11 Numerical results of the energy absorption of sandwich cylinder shells with different A and N

当N>4 时，结构的SEA 随着A的减小而增大。这是由于A的减小使内圆柱壳的直径增大，而内圆柱壳直径增加使结构支撑刚度上升，结构的EA 和SEA 增加。但是当N=4 时，结构的SEA 随着A的减小先增大后减小；当A=11 时，SEA 达到峰值。这是由于当N=4，A较大时，芯层结构不能起到很好的支撑作用，致使结构出现整体屈曲，EA 减小，SEA 下降[14]。从图12 可以看出，内壳和夹芯的SEA 都随着A的减小先增大后减小，外壳的SEA 基本不变。内壳和夹芯的SEA变化可以反映各部分的支撑力变化，因此支撑作用也随着A的减小先增大后减小。

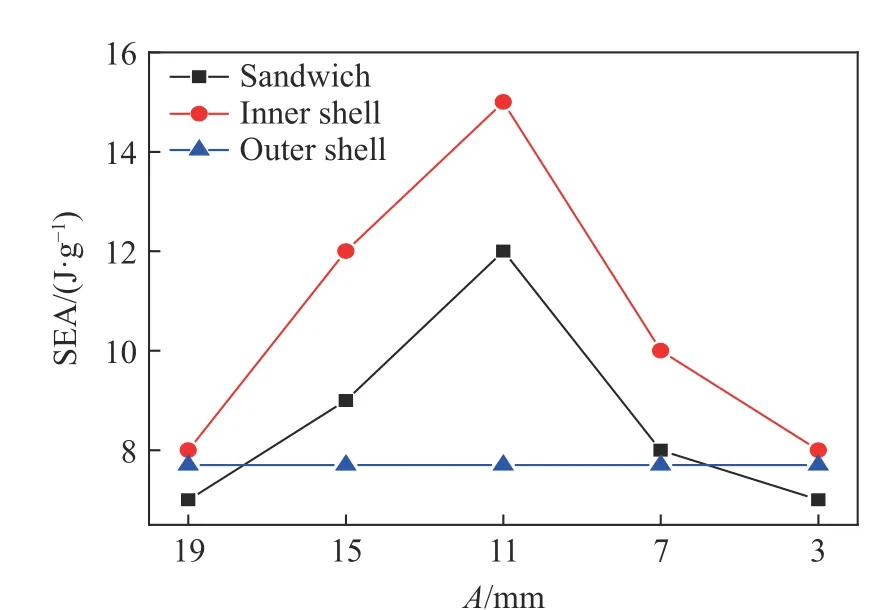
图12 N=4 时内外壳和夹芯的比吸能Fig. 12 Specific energy absorption of inner and outer shells and sandwich with N=4

如图13 所示，在A<15 mm 的条件下，夹芯圆柱壳的最优SEA 出现在结构发生轴对称变形时，而且SEA 随着变形模式的改变而变化。除了A=3 mm 外，结构的变形模式都随着N的增加从混合模式过渡到非轴对称模式再变为轴对称模式，表明在夹芯圆柱壳的轴向压缩过程中，轴对称变形模式能提高SEA。但是在A≥15 mm 的条件下，轴对称变形模式下的SEA 并不是最优，这是由于A较大时，结构的质量随着N的增加而增大（见图10）。虽然结构变形模式的改变使结构吸能增加，但是质量也增加得更多，导致变形模式的改变未能有效地提高SEA，甚至有所降低。

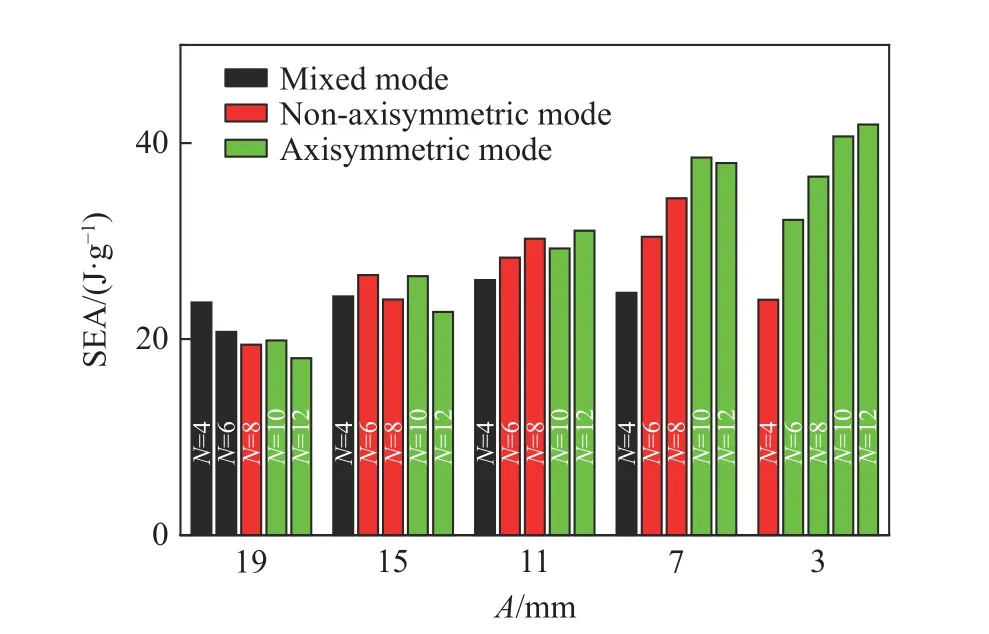
图13 不同的A 和N 下夹芯圆柱壳的比吸能和变形模式Fig. 13 Specific energy absorption and deformation modes of sandwich cylindrical shells with different A and N

综上可知，A和N控制着夹芯圆柱壳的变形模式，从而影响结构的SEA。当A<15 时，最佳SEA 出现在结构发生轴对称变形时。因此，要合理地选择A和N才能获得较优异的吸能结构。

3.2 冲击速度对结构变形模式和吸能的影响

为探究冲击速度对结构变形模式和吸能性能的影响，选择SEA 较高的4 个夹芯结构，分别为A7N10、A7N12、A3N10、A3N12。

如表1 所示，随着冲击速度的提高，结构的SEA 增大。在高速冲击下，夹芯圆柱壳具有良好的吸能特性，且A=7 mm 的圆柱壳的SEA 优于A=3 mm 的圆柱壳。如图14 所示，A=7 mm 的夹芯圆柱壳在高速冲击下发生非轴对称变形，具有较高的SEA，且A7N12 具有最高的SEA。

表1 不同冲击速度下结构的能量吸收对比Table 1 Comparison of energy absorption of structures at different impact velocities

为了更直观地观察变形模式，图14 显示了不同冲击速度下试样的变形模式。不同结构在不同冲击速度下发生的变形模式存在差异，表明冲击速度影响结构的变形模式。当冲击速度为20 和30 m/s 时，A7N12 夹芯结构均发生非轴对称变形，而其余结构发生混合变形或轴对称变形。

图14 不同冲击速度下夹芯圆柱壳的变形模式Fig. 14 Deformation patterns of sandwich cylindrical shells impacted at different impact velocities

4 结 论

通过实验和数值模拟研究了正弦波纹夹芯双圆柱壳的轴向压缩行为。通过改变夹芯结构参数，共得到25 种夹芯结构，利用有限元方法对不同冲击速度下的结构响应进行数值模拟，得到如下结论。

(1) 在轴向压缩过程中，随着夹芯厚度A和周期数N的变化，会产生不同的变形模式。在本研究的工况中，夹芯圆柱壳产生了轴对称、非轴对称、混合3 种变形模式。

(2) 轴向压缩模拟结果表明，当A<15 mm 时，最佳SEA 出现在结构发生轴对称变形时。在准静态压缩过程中，A=3 mm，N=12 的夹芯圆柱壳具有轴对称变形模式和较轻的质量，因而具有最优的EA 和SEA。

(3) 在准静态压缩下，A3N12 夹芯圆柱壳具有最高的SEA，发生轴对称变形；在冲击加载下，发生非轴对称变形模式的A7N12 具有最高的SEA和平均压缩力效率。