高压下G2ZT 晶体结构、电子结构和光学性质的第一性原理研究

李 佐，刘 云，廖大麟，成丽红

（贵州工程应用技术学院理学院, 贵州 毕节 551700）

富氮含能材料是一类低感度推进剂和烟火添加剂，广泛应用于气体发生器。（双3, 4, 5-三氨基-1,2, 4-三唑）-5, 5′-偶氮四唑（G2ZT）由德国科学家Klapötke 研制，是一种富氮、高能、钝感的火炸药[1-3]。实验研究表明，该材料含有78.2%的氮元素，爆炸燃烧后释放的气体主要为二氧化碳、氮气和水，与传统炸药相比，环境污染和安全危害小，因此被称为“绿色”含能材料[4-5]。G2ZT 晶体内部呈分子层状结构，分子间存在弱相互作用。目前，未见G2ZT 晶体高压物性的理论研究。Dreger 等[6]采用实验和第一性原理方法研究了新型含能材料TKX-50 晶体和分子结构随压强的变化关系，理论和实验结果符合较好。最近的研究表明，当脉冲激光照射并点燃含能材料RDX 时，可引起RDX 的光热解效应[7]。通过红外光谱技术，可以获得RDX 的特征化学键和晶格振动信息[8]。因此，含能材料的光学性质也是这一研究领域的重要方向。

本研究基于密度泛函理论的第一性原理研究G2ZT 晶体在0～40 GPa 静水压下的晶格参数、物态方程、结构演化、电子结构和光学性质。为了更好地描述G2ZT 晶体内部分子间的弱相互作用，分别采用密度泛函能量色散校正（PBE-D2）和范德瓦尔斯修正（vdW-DF2）方法计算，并采用Hirshfeld表面分析方法研究高压下分子间弱相互作用的强弱。同时，采用TB-mBJ 势计算G2ZT 晶体在高压下的电子结构，在此基础上获得晶体的光学性质。

1 理论模型和计算方法

1.1 理论模型

G2ZT 晶体为三斜结构的分子晶体，每个晶胞中包含2 个C2N6H7分子和1 个C2N10分子（共42 个原子），晶格参数a=5.261 9 Å，b=6.698 0 Å，c=11.884 0 Å， α=102.05°， β =90.8°， γ=109.96°。用以上实验数据作为初始构型进行理论计算，图1 为G2ZT 晶体晶胞结构和分子模型。

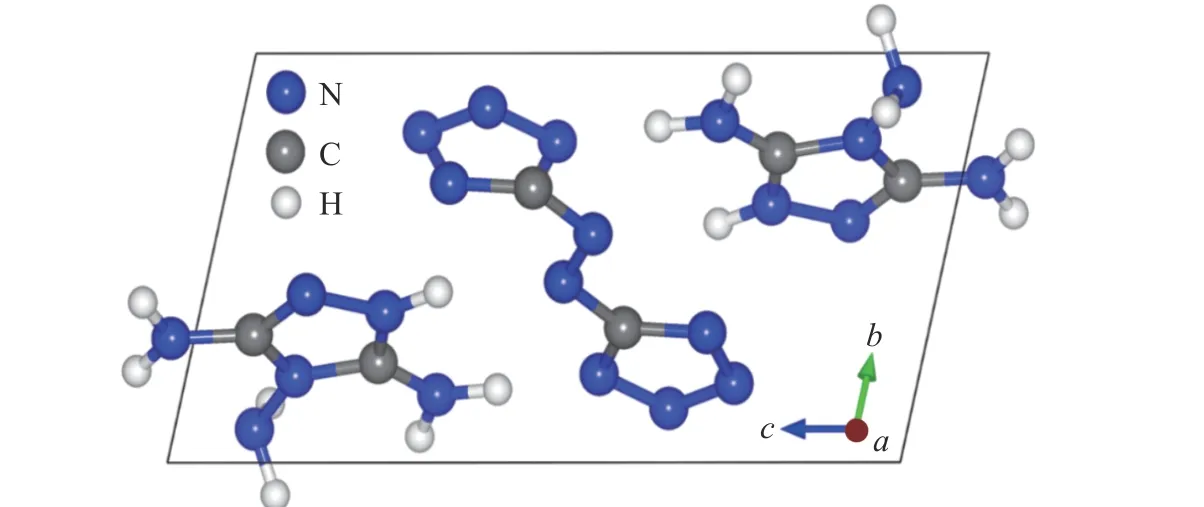
图1 G2ZT 晶体的晶胞结构和分子模型Fig. 1 Cell structure and molecular model of G2ZT crystal

1.2 计算方法

在密度泛函理论框架下，采用SIESTA 程序包中的共轭梯度最小分子动力学方法对G2ZT 晶体结构进行优化[9-11]。首先计算晶体结构中的原子位置和晶格参数，然后对其施加各向同性应力。在0～10 GPa和15～40 GPa 压强范围内，分别间隔1 和5 GPa 进行计算。一方面，采用Dion 等[12]发展的范德瓦尔斯密度泛函（vdW-DF）描述共价性和范德瓦尔斯弱相互作用。在vdW-DF 理论中，交换关联能（Exc）被定义为

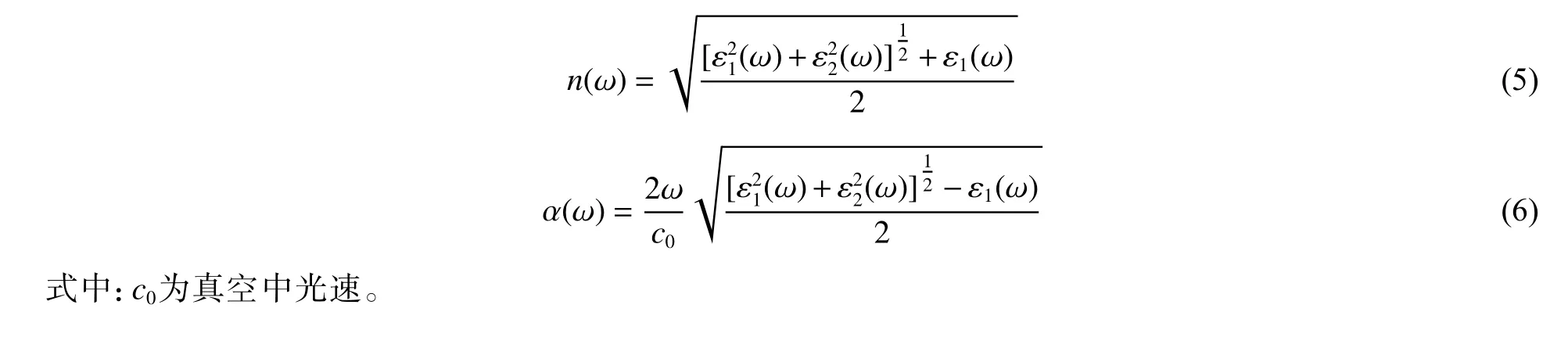
2 结果与讨论

2.1 晶体结构和物态方程

表1 列出了采用vdW-DF2 和PBE-D2 两种方法优化后晶格参数的理论计算结果及其与实验数据[2]的相对误差（ δvdW-DF2和 δPBE-D2）。可以看出，整体上理论计算结果的误差较小。其中采用vdW-DF2 方法计算的晶胞角度与实验值符合很好，尤其是α，其计算结果与实验值的相对误差仅为0.3%。采用PBED2 方法计算的a相对误差为1.7%，小于vdW-DF2 的计算结果。

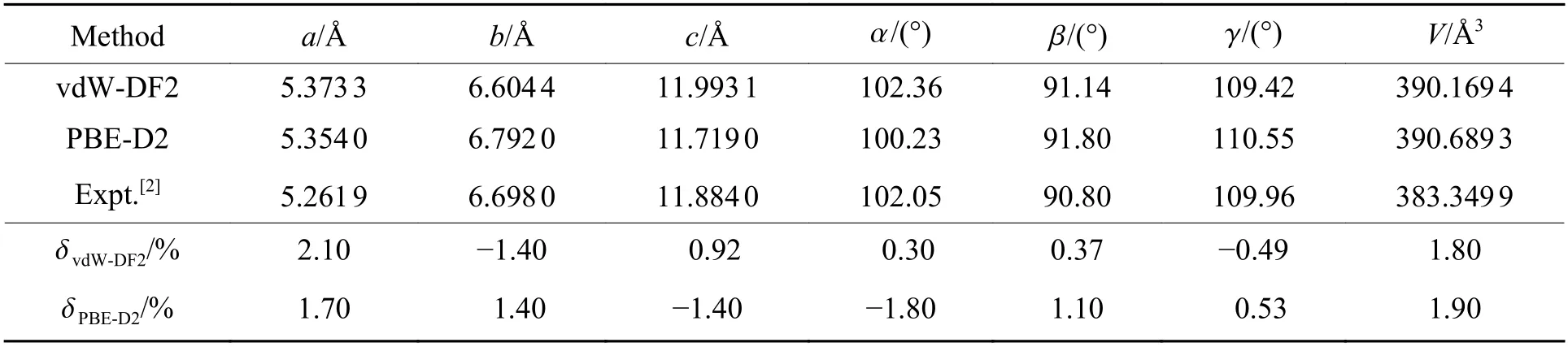
表1 G2ZT 晶格参数的计算结果和实验结果比较[2]Table 1 Calculated crystal lattice parameters of G2ZT compared with experimental data[2]

为进一步比较vdW-DF2 和PBE-D2 两种方法对高压下G2ZT 晶体特征的描述，图2 给出了晶格参量a、b、c和体积比V/V0随压强的变化关系。图2(a)显示：对于晶格参数a，其压缩率不高，在0～30 GPa的压强范围内，vdW-DF2 和PBE-D2 方法给出的结果完全一致；晶格参数b的压缩变化在0～10 GPa 范围内明显，之后趋缓；由vdW-DF2方法获得的晶格参数c随压强呈近线性变化，在0～40 GPa 范围内压缩率达10.2%。图2(b)显示：在0～5 GPa 范围内，两种方法给出的体积比非常接近；高压下，两种方法所得结果的差异逐步增大，当压强增加到40 GPa 时，PBE-D2 方法得到的体积比约为0.60，而vdW-DF2方法约为0.65，说明高压下两种计算方法在晶体几何结构的描述上有差异。

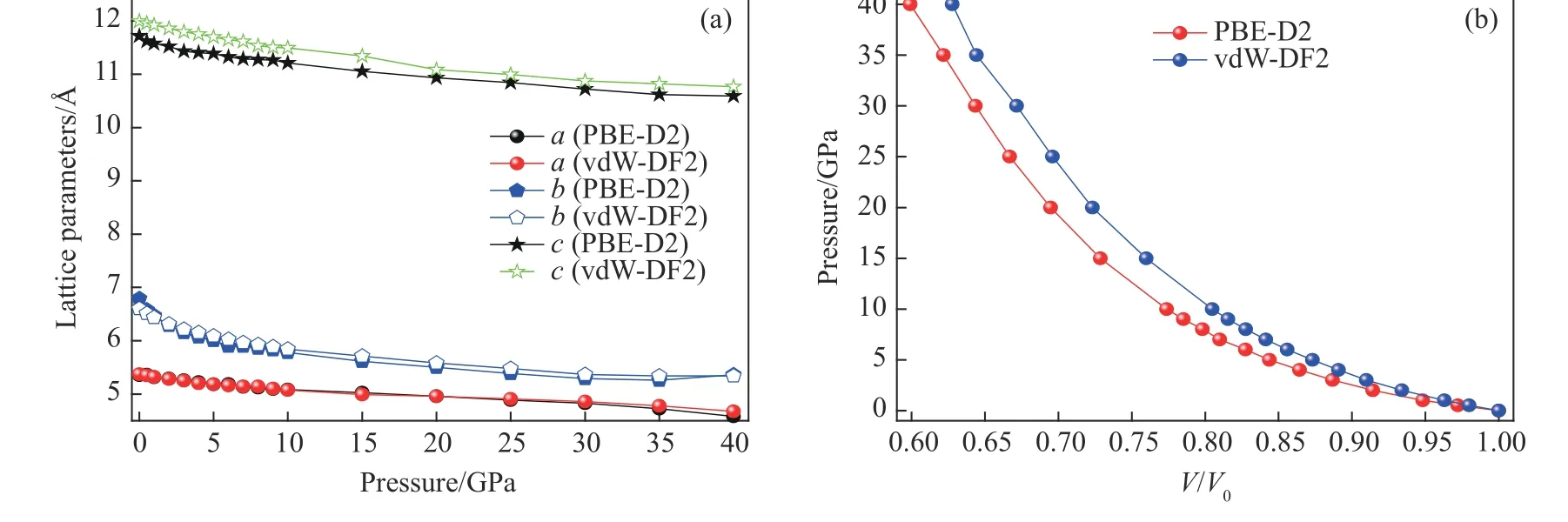
图2 G2ZT 晶体的晶格参数和体积比随压强的变化Fig. 2 Lattice parameters and V/V0 of G2ZT crystal versus pressure

此外，采用三阶Birch-Murnaghan（BM）[24]或者Vinet[25]物态方程拟合压强与体积比的关系，获得材料的体弹模量。三阶BM 和Vinet 物态方程的表达式分别为

表2 三阶BM 和Vinet 物态方程拟合得到的G2ZT 晶体的体弹模量及其一阶导数Table 2 Bulk moduli and their pressure-derivatives of G2ZT crystal determined by third-order BM and Vinet equations of state

2.2 高压下分子间相互作用的演变

采用Crystal Explorer 软件[28]计算G2ZT 晶体的三维Hirshfeld 面及其二维指纹图，计算结果如图3、图4 所示。首先，分析三维Hirshfeld 面。图3(a)、图4(a)分别记录了0 和40 GPa 下C2N10分子周围键长的分布特征，红-白-蓝3 色标记了范德瓦尔斯作用范围。很明显，随着压强增大，红色区域增多，蓝色区域减少，即增大压强后分子间距减小。其次，分析分子间相互作用。图3(b)和图4(b)为二维指纹图，可以看出，随着压强增大，指纹图面积减小，说明区域内分子间成键强度减弱。G2ZT 晶体的分子间相互作用主要来源于氢键，C2N10和相邻C2N6H7分子间存在氢键相互作用。图3(c)和图4(c)分别给出了0 和40 GPa 下N…H 键的数目，压强从0 GPa 增大至40 GPa 的过程中，N…H 键数量由73.2%下降到63.4%，变化明显，说明压力下分子的各向异性增强。图3(d)和图4(d)显示，C…H 键与N…H 键的表现类似，随着压力的增大，C…H 键数量下降，且成键面积（灰色部分）更小。以上分析表明，三维Hirshfeld 面及其二维指纹图可以描述压力对层状G2ZT 分子晶体几何结构的影响。

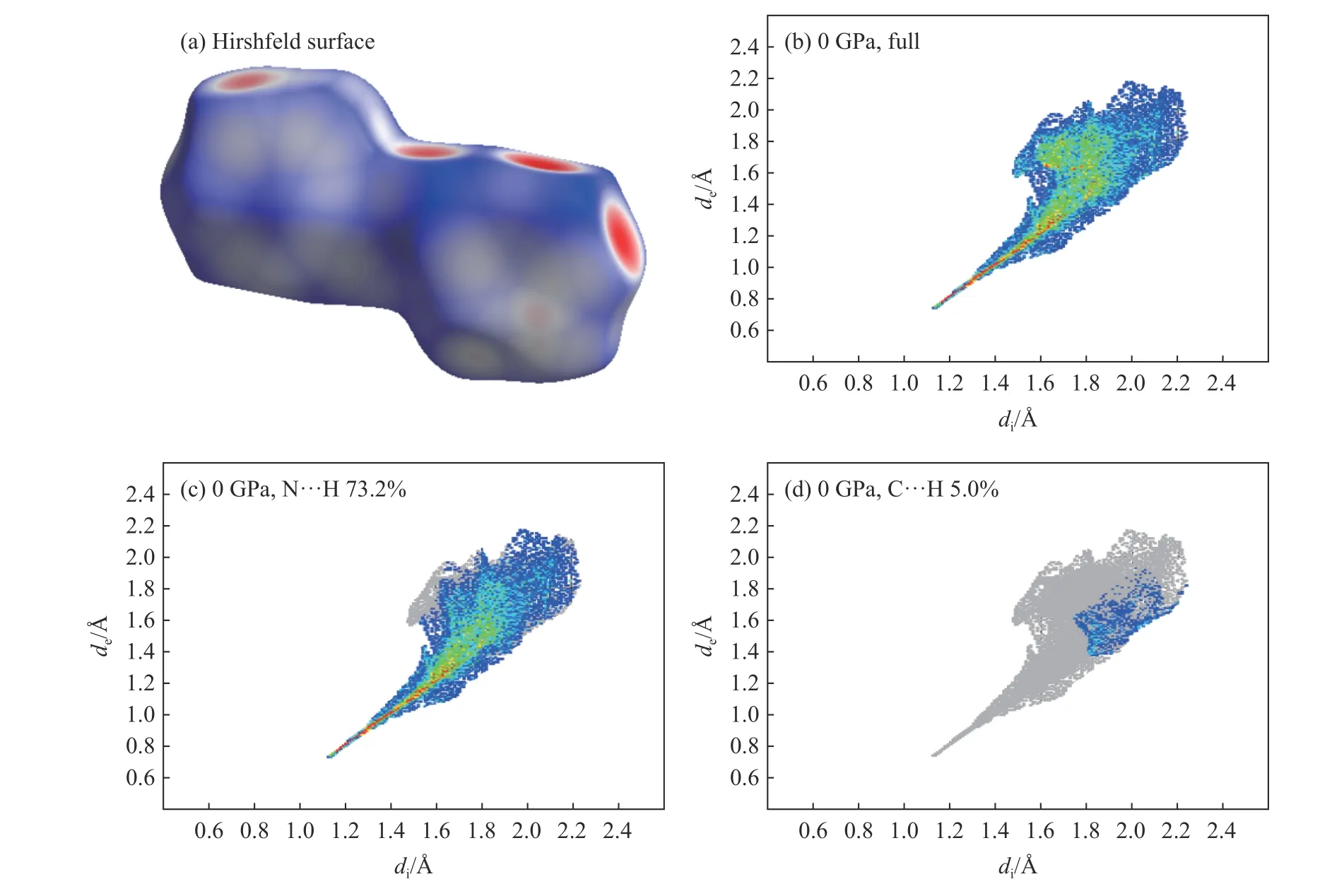
图3 C2N10 分子在0 GPa 下的Hirshfeld 面和二维指纹图Fig. 3 Hirshfeld surface and two-dimensional finger patterns of C2N10 molecule at 0 GPa

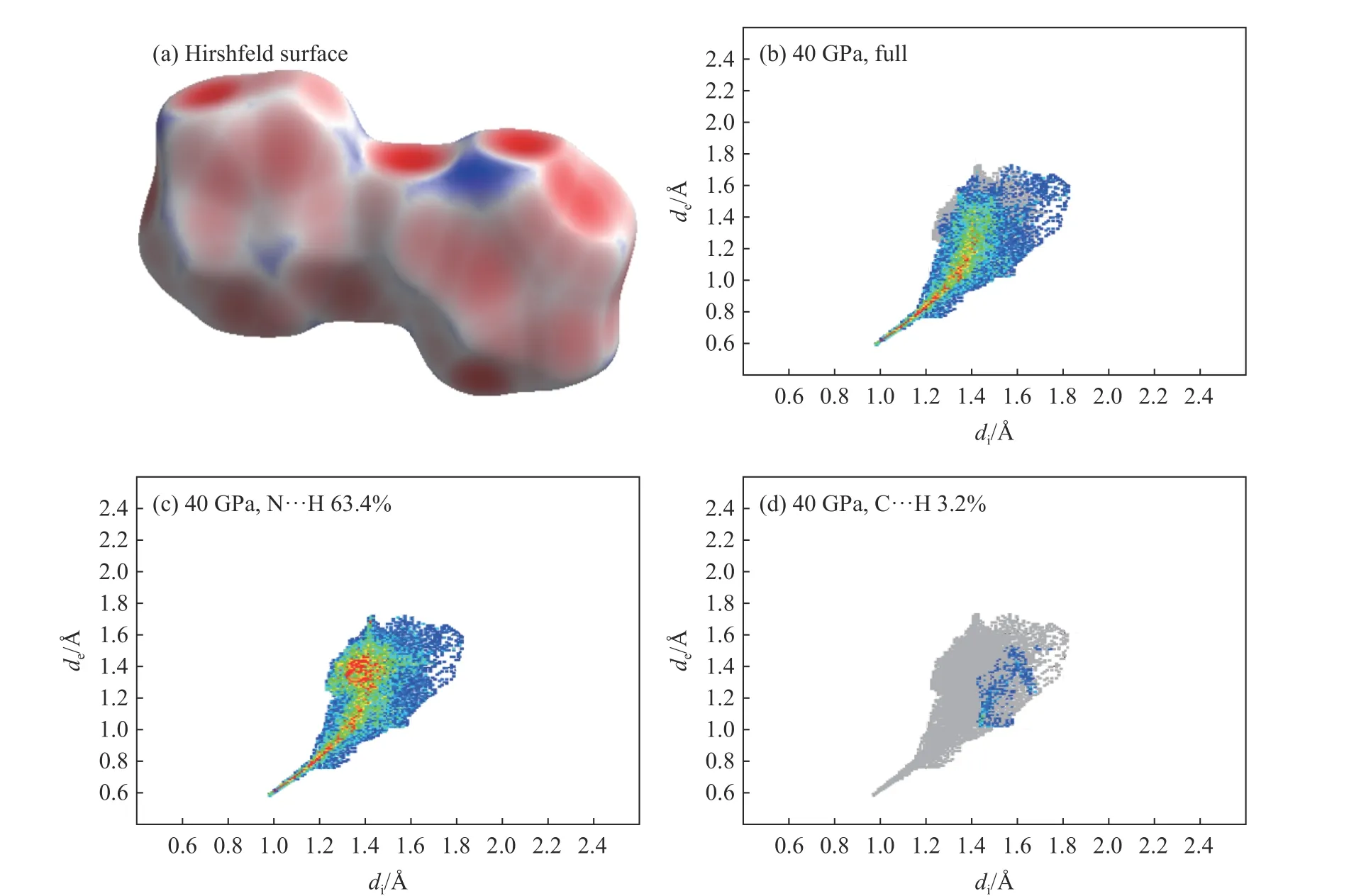
图4 C2N10 分子在40 GPa 下的Hirshfeld 面和二维指纹图Fig. 4 Hirshfeld surface and two-dimensional finger patterns of C2N10 molecule at 40 GPa

2.3 电子性质

G2ZT 分子晶体费米能级附近的能带变化影响其电子结构和光学性质。计算了-23.4～20.0 eV 能量范围内沿第一布里渊区高对称点方向的能带结构和电子态密度（density of states，DOS），共计得到导带和价带的163 条能级。图5 给出了-3.0～7.3 eV 能量范围内的能带结构片段，费米能级附近有28 条能级，其中价带18 条，导带10 条。零压下的能带结构如图5(a)所示，费米能级设置在0 eV 处，能量在-1.0～2.0 eV 范围内的4 条能带决定了带隙（导带底Ec和价带顶Ev之间的能量差）的变化。PBE 方法（蓝线）获得的高对称点M处的直接带隙为1.12 eV，而TB-mBJ 方法（黑线）获得的直接带隙为2.03 eV。同时，可以发现，两种方法获得的价带顶并无明显差别，但是导带变化明显。TB-mBJ 方法考虑了与轨道无关的交换关联势，因此，非占据态位置上移，导带底升高，相较于PBE 方法，带隙更大。图5(b)、图5(c)、图5(d)分别为3、10、40 GPa 下采用TB-mBJ 方法计算获得的能带色散关系。随着压强增大，晶格常数和分子内键长减小，高对称点之间能带曲线变得陡峭；同时，导带底靠近费米能级，带隙变窄。为深入分析各个高对称点处的能隙变化，统计了不同压强下第一布里渊区高对称k点在价带顶Ev和导带底Ec处的特征能量，列于表3 中。表3 显示：在低压下X与M高对称点之间存在平带，表明这个方向上电荷局域化程度较高；0 GPa 时，Γ 与X之间的间接带隙达到2.25 eV，是最大带隙值；当压强达到40 GPa 时，M处的直接带隙减小为0.91 eV。综上所述，压力对G2ZT 晶体带隙的调控作用明显。

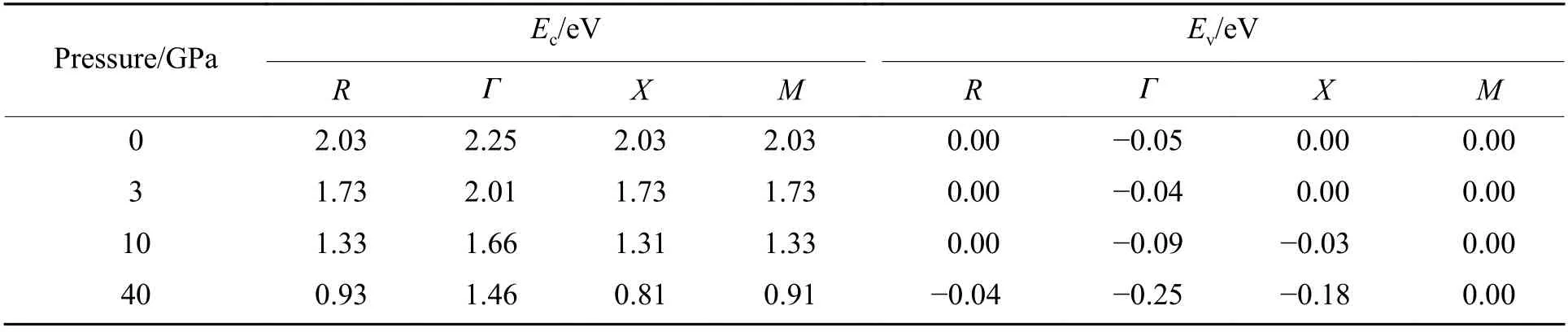
表3 不同压强下第一布里渊区高对称 k 点在价带顶 Ev 和导带底 Ec的特征能量Table 3 Characteristic energy values for top of valence band E v and bottom of conduction bandEc in highly symmetric k points of the first Brillouin region at different pressures

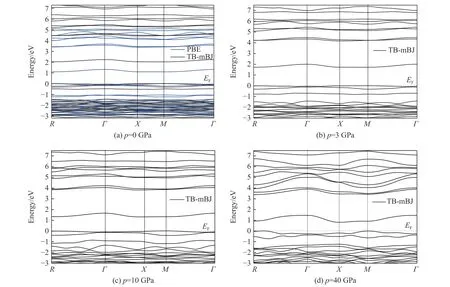
图5 G2ZT 晶体在不同压强下的能带色散关系Fig. 5 Energy band dispersion of G2ZT crystal at different pressures

为观察不同轨道电子对能带结构的贡献，计算了不同压强下G2ZT 晶体的总态密度和C、N、H 原子的分态密度分布，如图6 所示。图6 显示：费米能级附近的态密度主要由N-2p、C-2p 轨道电子贡献，费米能级进入价带中，表明G2ZT 晶体是一种p 型半导体；随着压强增大，带隙减小，态密度峰值强度减弱；10 GPa 下，导带能量2 eV 处的态密度峰值发生分裂，简并解除；同时，压强为40 GPa 时，价带在-1～0 eV 能量范围内的总态密度峰值也发生分裂，简并解除；在3、10 和40 GPa 下，H-1s 轨道电子对价带有贡献，说明高压下分子间的氢键作用明显。压强引起的态密度变化和能带结构变化是一致的。

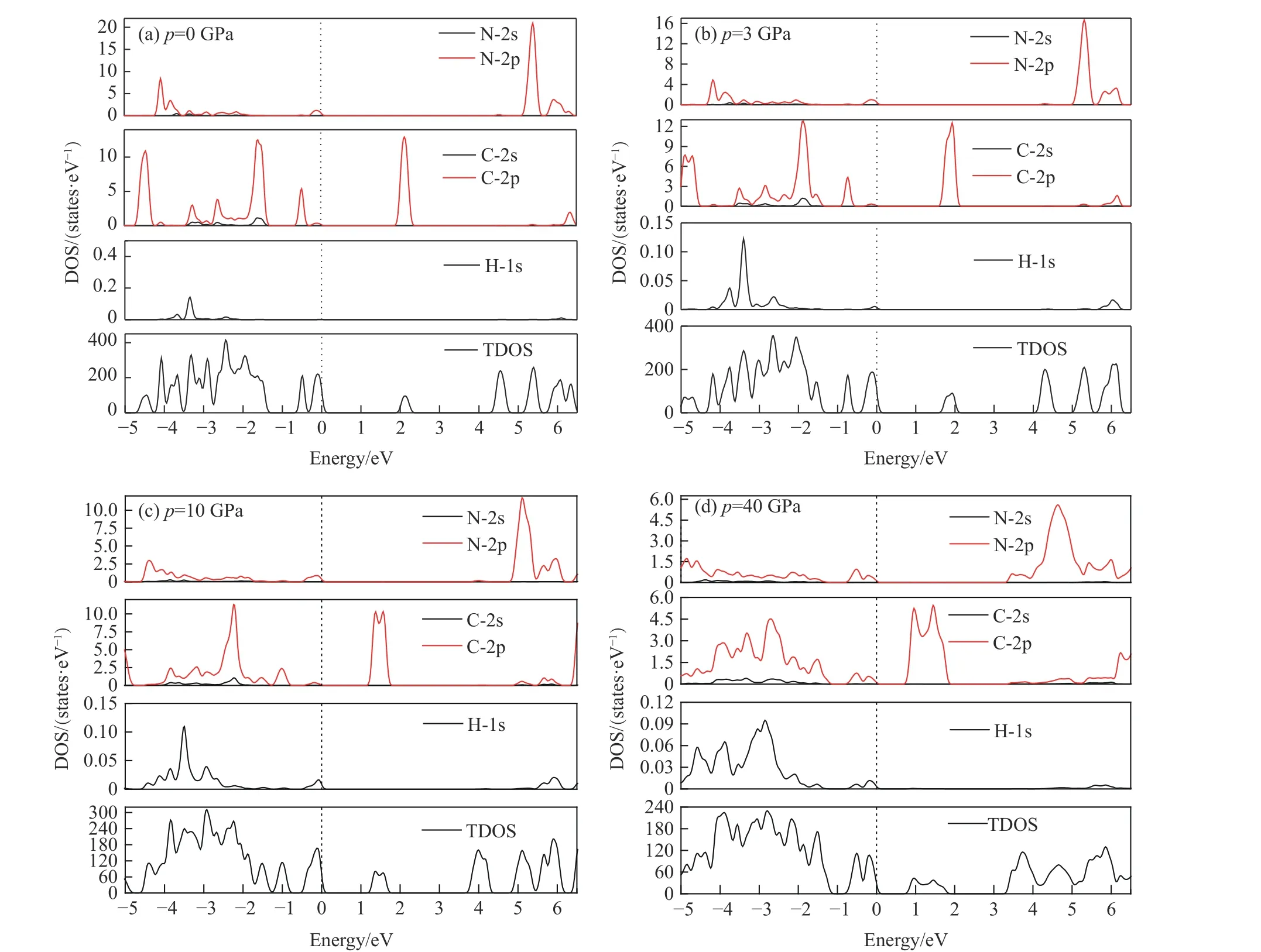
图6 不同压强下G2ZT 晶体的态密度分布Fig. 6 Distributions of DOS of G2ZT crystal at different pressures

2.4 光学性质

G2ZT 晶体属于三斜结构，入射光沿a、b、c3 个方向极化。光与物质相互作用时，电场起主导作用，极化方向记为E//x、E//y、E//z。图7 为0、3、10 和40 GPa 下介电函数随入射光能量的变化。其中，图7(a)、图7 (b)、图7(c)显示了3 个极化方向的介电函数实部 ε1(ω)。 以0 GPa 为例，静态介电常数实部ε1(0)在E//x、E//y、E//z3 个方向上分别为3.75、1.94、3.11，E//x方向的极化强度最大。压强从0 GPa 增加至40 GPa 的过程中，在0～3.39 eV 能量范围内，介电函数实部随着压强增大而增强，且最大值向低能方向移动。图7(d)、图7(e)、图7(f)显示了介电函数虚部 ε2(ω) ， 第1 个峰值位置出现在3.1 eV以内。与ε1(ω)相似，介电函数虚部 ε2(ω)在E//x方向的极化强度最大。随着压强的增大，第1 峰值向低能方向移动，与2.3 节中所述的能带带隙变化趋势相同。图7 显示，压强低于10 GPa 时，介电函数的变化趋势类似，无显著异常。因此，以下讨论反射率R(ω) 、折射率n(ω) 和 吸收系数 α(ω)时，只关注0 和40 GPa 下的变化。

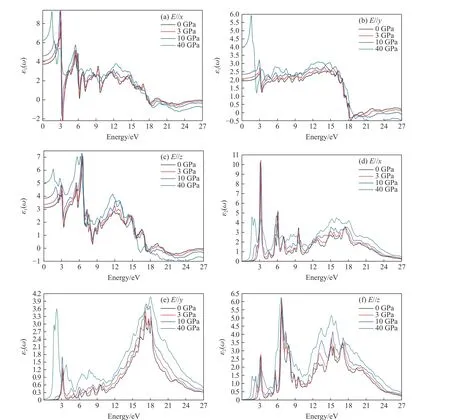
图7 不同压强下G2ZT 晶体的介电函数随入射能量的变化Fig. 7 Dielectric functions of G2ZT crystal versus incident energy at different pressures

图8 为G2ZT 晶体在0 和40 GPa 下的反射率R(ω)曲线。当压强为0 GPa 时，能量为3.1 eV 处，反射率达到最大值，E//x、E//y、E//z3 个方向上的反射率分别为45.0%、5.1%、15.0%，在紫外波段（3.1～10 eV）反射率达25.0%，在远紫外波段（10 eV 以上）反射率达32.5%。当压强为40 GPa 时，1.6～3.1 eV 能量范围内的反射率最大值为27.5%。说明G2ZT 晶体加压后对可见光的反射率降低，且材料具有各向异性。

图9 给出了G2ZT 晶体在0 和40 GPa 下的折射率n(ω)曲线。介质折射率与入射光频率（能量）有关。0 GPa 时，入射能量3.0 eV 处的折射率在E//x方向上约为3.1，在E//y方向上约为1.6，而在E//z方向约为2.1，随着入射能量升高，折射率在E//x、E//z方向上波动较大，而在E//y方向上3.0～15 eV 能量范围内，折射率呈较小的波动变化，与图8 中零压下反射率的变化类似，说明在E//y方向上晶体对入射能量的光学响应没有E//x、E//z方向上的强烈。在40 GPa 高压下，3 个方向上的折射率在可见光范围内的红光附近都有所增大，E//x方向上折射率达3.2。高压下折射率的增加与晶体密度的增大相对应。

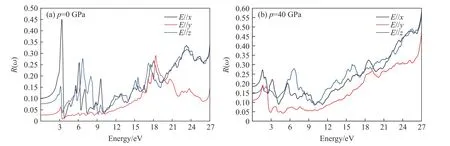
图8 G2ZT 晶体在0 和40 GPa 压强下的反射率随入射能量的变化Fig. 8 Reflection index of G2ZT crystal versus incident energy at 0 and 40 GPa

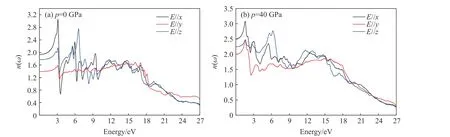
图9 G2ZT 晶体在0 和40 GPa 压强下的折射率随入射能量的变化Fig. 9 Refraction index of G2ZT crystal versus incident energy at 0 and 40 GPa

光吸收系数 α (ω)用于表征光在晶体中传播单位距离时的强度变化。图10 为G2ZT 晶体在0 和40 GPa下的吸收系数曲线。0 和40 GPa 下，光吸收系数的第1 个吸收峰都出现在可见光波段附近。零压下，E//x方向的吸收系数为7.5×105cm-1；当能量为19 eV 时，E//y方向的光吸收系数最大可达2.4×106cm-1，之后衰减。40 GPa 时，E//x、E//y方向的第1 吸收峰的峰值重合，E//z方向的光吸收系数最小，近紫外波段的第2 吸收峰相较于零压下衰减较多，高能区（大于19 eV）的吸收系数在E//x、E//z方向均有增强，E//x方向的吸收系数达到3.0×106cm-1，而E//y方向的吸收系数则与0 GPa 时保持一致，表明加压后材料的吸收系数也具有各向异性。

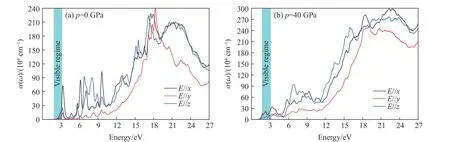
图10 G2ZT 晶体在0 和40 GPa 压强下的吸收系数随入射能量的变化Fig. 10 Absorption coefficient of G2ZT crystal versus incident energy at 0 and 40 GPa

3 结 论

基于密度泛函理论的第一性原理研究了高压下富氮含能材料G2ZT 的几何结构、电子结构和光学性质。压力对晶格常数的影响分析表明，PBE-D2 和vdW-DF2 两种方法计算获得的分子晶体结构数据与实验结果符合较好，误差均在3%以内。采用vdW-DF2 方法，通过三阶BM 和Vinet 两种物态方程拟合体积比与压强的关系曲线，得到G2ZT 的体弹模量分别为(27.58±0.76) 和(26.48±0.66) GPa。Hirshfeld 面分析表明：随着压强的增大，分子间氢键数目占比减小，说明氢键作用减弱。零压下，G2ZT 晶体的带隙为2.03 eV；随着压强增大，带隙变窄。零压和高压下G2ZT 晶体均为p 型半导体。在计算介电函数的基础上，获得了G2ZT 晶体的光学参量。0 GPa时反射率最大达45%，高压下吸收系数最大达3.0×106cm-1。研究结果为高压下G2ZT 晶体特征分析提供了理论参考。