冰雹载荷下基于碳纤维增强复合材料的腔棘鱼鳞双螺旋仿生结构的撞击损伤分析
韩登安,徐 丹,叶仁传,任 鹏
(江苏科技大学船舶与海洋工程学院, 江苏 镇江 212000)
近年来,随着材料科学的迅速发展,纤维复合材料因其质量轻、比模量高、比强度大、可设计性强、耐腐蚀等优点越来越多地应用于航空航天、船舶工程及汽车制造等领域[1-2]。轻量化结构在服役过程中,其表层复合材料构件易受到冲击载荷作用,例如飞机机翼受冰雹撞击、汽车复合材料外壳受石子冲击等,造成局部凹陷及破坏等损伤,从而影响结构的整体安全。因此,明确仿生复合结构在动态载荷下的力学行为及毁伤特性是有效提升其工程应用价值的关键。Dolati 等[3]研究了冰雹形状对面板为复合材料的夹芯结构的吸能特性的影响,发现冰雹弹头的尖锐度是影响面板损伤的重要因素。莫袁鸣等[4]研究了在冰雹高速冲击下T700/TDE-85 碳纤维层合板的损伤,发现正交铺层板抵抗分层的能力较强,准各向同性铺层板抵抗变形的能力更优异。Wang 等[5]研究了碳纤维增强层合板在高速冲击下的响应,得出低速冲击下层合板的主要失效模式为拉伸失效,而高速冲击载荷下的主要失效模式为剪切失效。刘建刚等[6]研究了冰雹冲击下复合材料T 型接头的损伤,发现T 型接头的分层面积与冰雹的撞击能量近似呈线性关系,分层面积和撞击力峰值随入射角的增大而增大。近年来,仿生复合结构的兴起为结构的抗冰雹设计提供了更多选择。张海广等[7]研究了冲击速度和试件长宽比对分支交错层状仿生复合结构的动态断裂韧性及裂纹扩展的影响,发现随着冲击速度和硬质材料长宽比的增大,裂纹越来越倾向于沿直线扩展,断裂韧性随试样总宽度的增大而增强。Shang 等[8]研究了落锤冲击下T700/2150碳纤维仿生螺旋结构的力学响应特性,发现结构的承载能力随螺旋角的减小而增大。在此基础上,王瑜等[9]分析了不同基体材料(软质基体Tango Plus 和硬质基体VeroWhite Plus)的仿生螺旋结构的断裂韧性与螺旋角的关系,发现螺旋角在0°~75°之间时,螺旋角增大,则试件的断裂韧性增强。田野等[10]研究了新型仿生蛛网结构抗跌落物缓冲特性,结果表明,仿蛛网缓冲结构可使跌落物的加速度下降86%。到目前为止,前人对仿生结构在硬物冲击下的研究较多,而对冰雹载荷下的动态响应却鲜见报道。近期,Yin 等[11]基于腔棘鱼鳞片的双螺旋结构,提出了新型仿生纤维结构,研究表明,该双螺旋仿生结构具有良好的抗撞击性能,其优异的抗冲击特性为冰雹防护结构设计提供了新的思路。
为此,本研究基于双螺旋仿生结构的增韧特性,结合数值模拟对腔棘鱼鳞双螺旋仿生结构在冰雹撞击载荷下的力学响应进行研究,对比分析在相同的密度条件下腔棘鱼鳞双螺旋仿生结构和正交层合结构在冰雹撞击下的防护及毁伤特性。
1 有限元模拟
1.1 腔棘鱼鳞双螺旋仿生结构有限元模型
采用Yin 等[11]提出的腔棘鱼鳞双螺旋仿生结构,该结构受腔棘鱼鳞片的双螺旋状胶原纤维结构的启发,将单向碳纤维板按指定螺旋角构成,如图1(a)所示[11]。双螺旋仿生结构与正交层合结构均由20 层单向碳纤维板构成,铺层顺序分别为[0°/90°/20°/110°/···/180°/270°]、[0°/90°]5s,每层碳纤维单向板厚度为0.25 mm。定义纤维的轴向为x方向,面内与纤维轴向垂直的方向为y方向,上表面外法向为z方向。
有限元模型如图1(b)所示,冰雹直径为60 mm,双螺旋仿生结构与正交层合结构不能视为各向同性材料,为此,采用全模型计算。两种结构的尺寸均为300 mm×300 mm×5 mm,撞击区域的网格尺寸为0.50 mm×0.50 mm×0.25 mm。部件均采用八节点线性缩减积分单元(C3D8R)划分,边界条件为四周固支,冰雹撞击方向为面板法向。
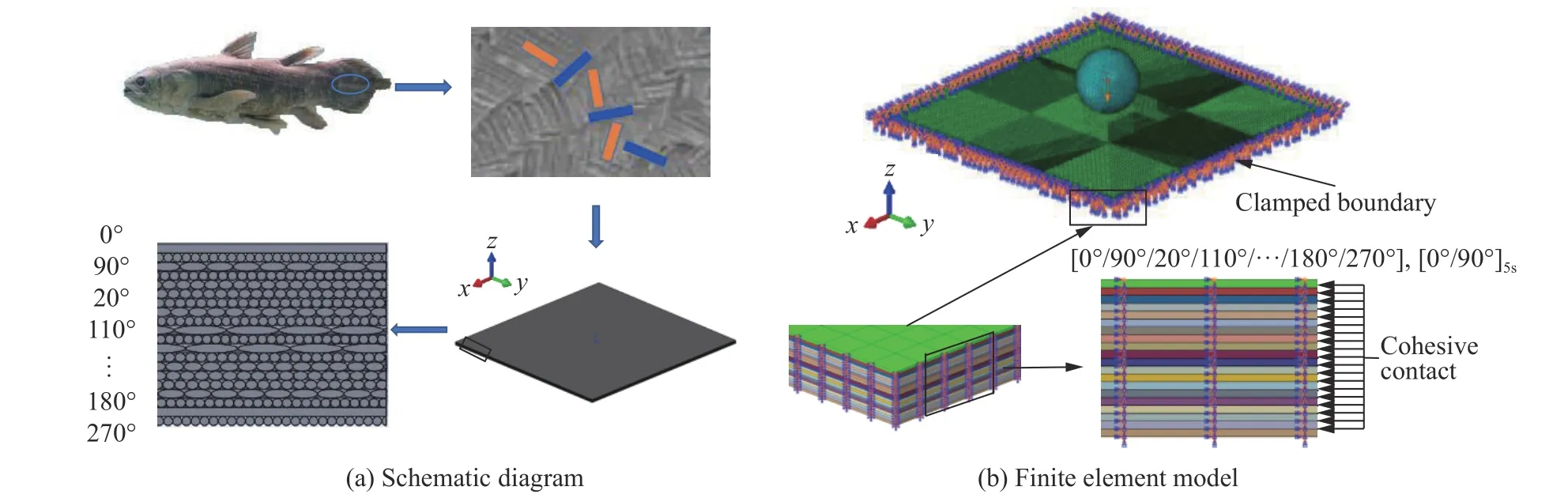
图1 双螺旋仿生结构Fig. 1 Double-helicoidal bionic structure
1.2 材料模型及损伤演变
纤维增强复合材料的本构模型选择正交各向异性材料的应力-应变关系。选择Shokrieh 等[12]提出的三维Hashin 失效准则描述碳纤维复合材料的失效,具体表达式如下


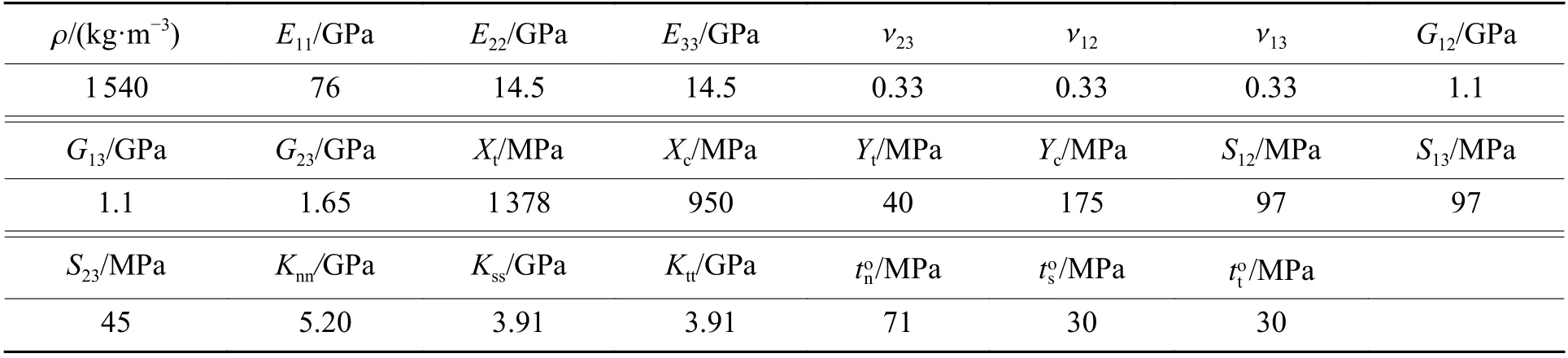
表1 碳纤维单层板材料参数及层间强度参数Table 1 Carbon fiber unidirectional plate material and interlaminar strength parameters
考虑到应变率对冰雹在高速冲击下的力学性能的影响较大,应用陈星[14]提出的冰雹材料模型:以应变率相关的抗压强度关系为本构模型,材料单元的分离准则选用张力失效准则(张力失效准则适用于高应变率下材料因张力而发生的失效)。抗压强度受应变率影响,不同撞击速度下的抗压强度不同,在ABAQUS 中通过不同应变率对应的抗压强度比(各应变率节点的抗压强度与初始屈服强度的比值)实现,如表2 所示。冰雹的力学性能参数如表3[14]所示。

表2 冰雹的材料参数Table 2 Material parameters of the hail

表3 冰雹的材料参数[14]Table 3 Material parameters of the hail[14]
1.3 模型有效性分析
为验证冰雹模型的有效性,模拟直径为61 mm 的冰雹以62 m/s 的速度撞击刚体,获得了冰雹的接触力时程曲线,对比文献[15]中Test 191 的实验结果[15],如图2(a)所示,可以看出,两者具有较好的一致性。说明采用该模型可以有效地模拟冰雹在撞击过程中的塑性变形及流动,冰雹材料模型是有效的。

图2 实验[11,15]和数值模拟得到的接触力曲线及损伤对比Fig. 2 Comparisons between experiment[11,15] and simulation of contact force curve and damage appearance
为验证双螺旋仿生结构模型的有效性,将数值模拟结果与文献[11]中试件DH-20 的接触力曲线及损伤进行对比,如图2(b)所示[11]。实验和数值模拟得到的接触力峰值分别为1.05 和1.11 kN,相对误差为5.7%,比吸能分别为163.46、170.65 kJ/m2(双螺旋仿生结构的比吸能定义为吸收的能量除以试件宽度与厚度的乘积),相对误差为4.5%。另外,数值模拟得到的双螺旋仿生结构的断裂路径与实验结果一致。对比接触力-位移曲线、比吸能及断裂路径,结果表明,双螺旋仿生结构模型是有效的。
2 数值模拟结果分析
2.1 仿生结构与正交层合结构的毁伤对比分析
冰载荷是结构安全的较大隐患。自然界中冰雹的直径通常在25~60 mm 之间,相对于工作中的航行体,其相对速度可达50~150 m/s。为模拟极端工况,冰雹直径取60 mm,撞击能量选择127.7~1 149.3 J,通过研究撞击能量和冰雹分布密度对双螺旋仿生结构和正交层合结构动态响应的影响,对比分析两种结构在冰雹载荷下的毁伤特性。考虑到结构达到稳定状态所需的计算量较大,为此认为结构与冰雹之间的接触力小于峰值的10%时加载过程结束[11]。
图3(a)为两种结构在冰雹高速撞击下的接触力时程曲线。接触力峰值均在0.09 ms 出现,分别为40.2 和39.1 kN。0.09 ms 以后,正交层合结构的接触力迅速下降且波动明显,0.30~0.50 ms 时趋于平稳,最后接触力逐渐减小;而双螺旋仿生结构的接触力在0.09 ms 后缓慢下降,0.60~0.90 ms 时出现波动,这是因为结构回弹时与冰雹再次碰撞。图3(b)为两种结构的撞击点位移-时间曲线,可以看出,正交层合结构的撞击区域破坏严重,而双螺旋仿生结构在0.48 ms 时开始回弹直至稳定。
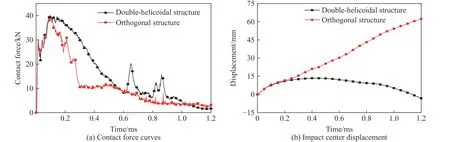
图3 相同撞击能量下双螺旋仿生结构和正交层合结构的响应曲线Fig. 3 Response curves of double-helicoidal bionic structure and orthogonal laminated structure under the same impact energy
图4 显示了两种结构在冰雹高速撞击下的动态损伤,其中:损伤单元用红色显示,未损伤单元用蓝色显示。在0~0.20 ms 之间,两种结构在撞击区域均出现基体拉伸失效及面外凸起,接触区域四周发生分层。在0.20~0.40 ms 之间,两种结构的分层向面内四周扩展,随着冰雹载荷对结构持续作用,较大的撞击力导致纤维基体发生拉伸、挤压等损伤。0.48 ms 之后,双螺旋仿生结构的撞击点达到最大位移并开始回弹,1.30 ms 时接触力已小于峰值的10%,加载过程结束,但结构仍处于回弹阶段,经过平衡位置时撞击点由于惯性作用继续向前运动,因此后期出现负位移。对于正交层合结构,在载荷的持续作用下,0.60 ms 时撞击区域出现裂纹,最后发生严重基体破碎和纤维断裂。层间应力对结构的损伤机理起重要作用[11]。在高速撞击下,正交层合结构最初出现层间损伤和跨层裂纹,最终导致撞击区域完全失效;而双螺旋仿生结构仅出现浅表纤维断裂及层间损伤。
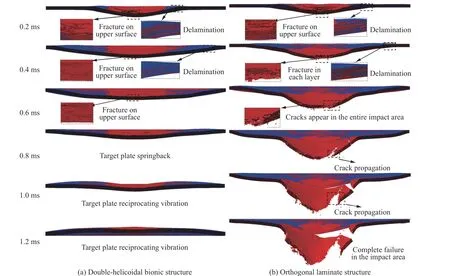
图4 冰雹高速撞击下双螺旋仿生结构和正交层合结构的动态损伤Fig. 4 Dynamic damage of double-helicoidal bionic structure and orthogonal laminated structure under hail high-speed impact
2.2 冰雹撞击能量对仿生结构动态响应的影响
改变冰雹速度以获得不同的撞击能量,研究双螺旋仿生结构在冰雹撞击下的力学响应。不同撞击能量下双螺旋仿生结构的接触力时程曲线见图5(a)。当撞击能量为127.7、287.3、510.8、798.1、1 149.3 J时,对应的接触力峰值分别为11.5、15.1、21.5、30.4 和40.2 kN。撞击能量越大,接触力峰值越大,且出现得越早。图5(b)为不同撞击能量下撞击点位移时程曲线,结合图5(a)可知,接触力峰值总是出现在撞击点达到最大位移之前。当撞击能量为127.7、287.3、510.8、798.1、1 149.3 J 时,对应的撞击点位移最大值分别为8.6、8.8、10.0、11.6、13.4 mm,结合图5(b)曲线上升阶段斜率可知,双螺旋仿生结构的最大位移与变形速度均随撞击能量的增大而增大。
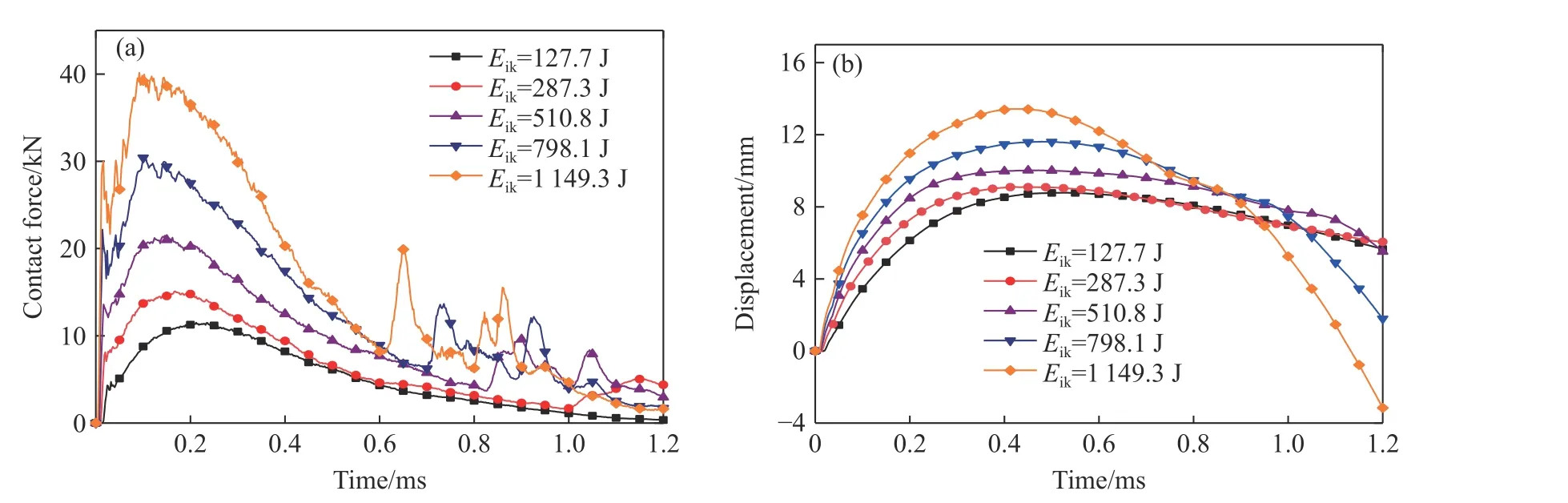
图5 不同撞击能量下双螺旋仿生结构的动态响应曲线:(a)接触力曲线,(b)撞击点位移曲线Fig. 5 Dynamic response curves of double-helicoidal bionic structure under different impact energies:(a) contact force curves, (b) impact center displacement curves
图6(a)给出了不同撞击能量下的接触力峰值,可见,接触力峰值随撞击能量的增大而线性增大。图6(b)显示了双螺旋仿生结构在不同撞击能量下的能量吸收比变化规律。随着撞击能量的增大,仿生结构出现数量更多、形式更复杂的损伤,吸收了更多的能量,双螺旋仿生结构的能量吸收比随撞击能量的增大而线性增大。
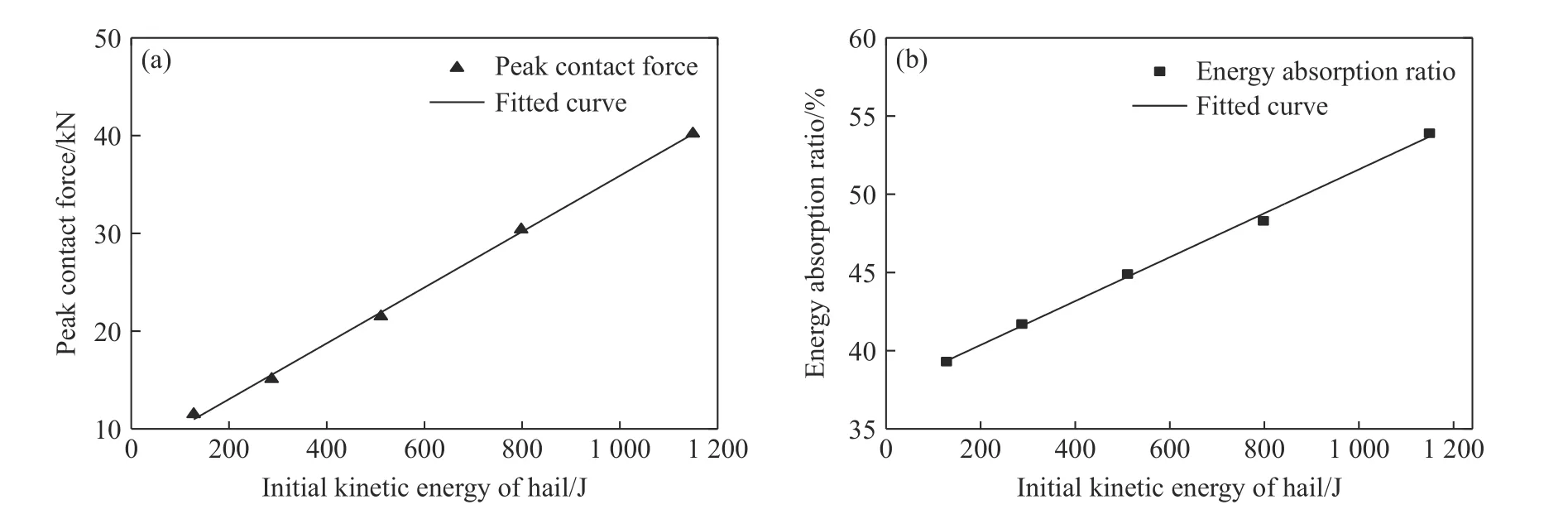
图6 不同撞击能量下双螺旋仿生结构的接触力峰值(a)和能量吸收比(b)Fig. 6 Peak contact force (a) and energy absorption ratio (b) of double-helicoidal bionic structure under different impact energies
冰雹高速撞击下两种结构的能量变化如表4 所示,其中:Eik为冰雹的初始动能,Eε为冰雹的总应变能,Erk为冰雹的剩余动能,Ea为结构吸收的能量,R为结构的能量吸收比。可以看出:当冰雹的初始动能为1 149.3 J 时,双螺旋仿生结构的能量吸收比相比正交层合结构低9.3%;当双螺旋仿生结构达到与正交层合结构一样的能量吸收比时,双螺旋仿生结构会承受更大的撞击载荷。对比分析损伤状态和能量吸收比可知,相比正交层合结构,双螺旋仿生结构具有更优异的抗冰雹撞击性能。
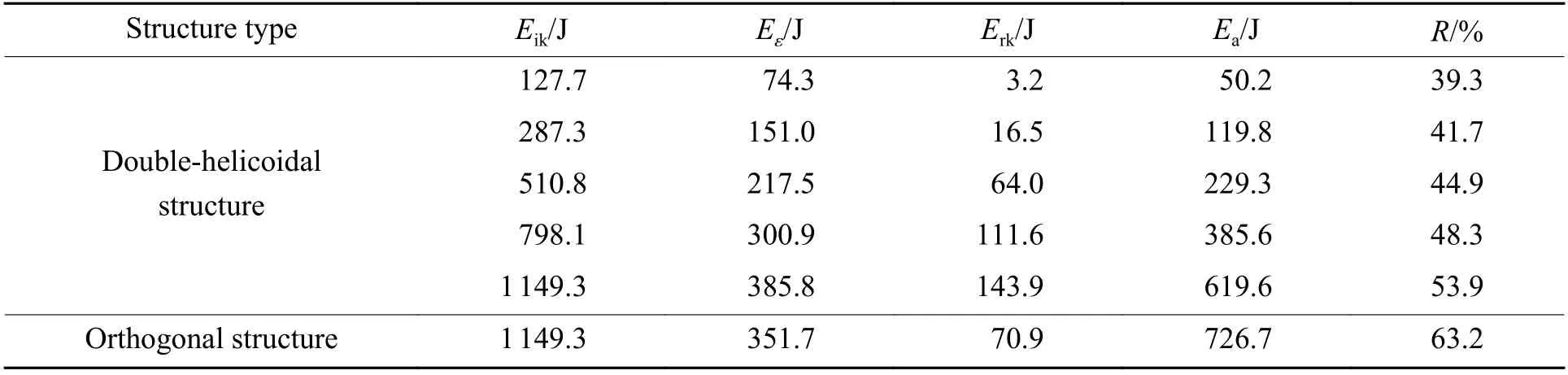
表4 不同结构的能量变化Table 4 Energy changes of different structures
不同的撞击能量下双螺旋仿生结构撞击点达到最大位移时的损伤如图7 所示。当撞击能量为127.7 J 时,损伤以撞击区域上表面y和z方向的基体拉伸失效为主;当撞击能量增加到510.8 J 时,撞击区域上表面发生以剪切为主的破坏形式,下表面开始出现纤维拉伸失效;当撞击能量增加到1 149.3 J 时,结构在撞击区域厚度方向发生明显损伤,且浅表出现分层,并伴随少量的纤维断裂。
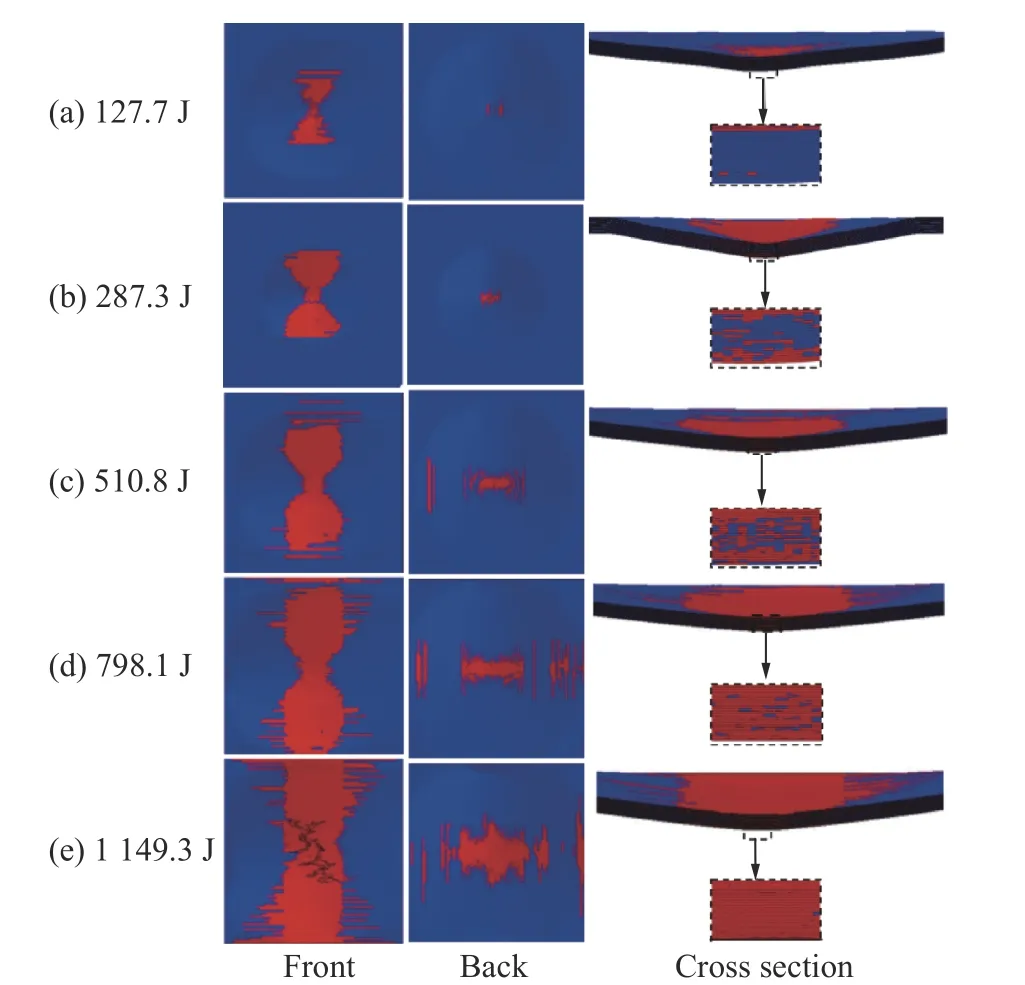
图7 不同撞击能量下双螺旋仿生结构的损伤Fig. 7 Damage of double-helicoidal bionic structure under different impact energies
2.3 冰雹分布密度对结构动态响应的影响
冰雹加载时,冰雹沿结构表面四周发生流动,与结构接触的区域视为等效撞击区域。为研究冰雹分布密度对双螺旋仿生结构力学响应的影响,建立了与单个冰雹等质量等体积但分布密度不同的冰雹以1 149.3 J 的撞击能量撞击双螺旋仿生结构的4 种工况,即H3、H5、H7、H9(数字表示冰雹个数)。图8 展示了不同工况下双螺旋仿生结构的损伤。由图8 可知:随着冰雹分布密度的增大,双螺旋仿生结构上表面的损伤程度逐渐减小(在工况H9 中双螺旋仿生结构的上表面不再发生纤维断裂),下表面的损伤面积逐渐增大,同时厚度方向的损伤程度逐渐减小。冰雹分布密度的改变将引起冰雹半径变化。当冰雹的半径较小时,双螺旋仿生结构的损伤形式以基体开裂为主;而当冰雹的半径较大时,则以基体开裂和浅表纤维断裂为主。

图8 双螺旋仿生结构在不同冰雹分布密度下的损伤Fig. 8 Damage of double-helicoidal bionic structure under different hail distribution densities
在不同的冰雹分布密度下,双螺旋仿生结构等效撞击中心最大位移的变化曲线如图9 所示。可以看出,在单个冰雹撞击下双螺旋仿生结构等效撞击中心的最大位移为15.8 mm,等效撞击中心的最大位移随冰雹分布密度的增大呈抛物线递减。
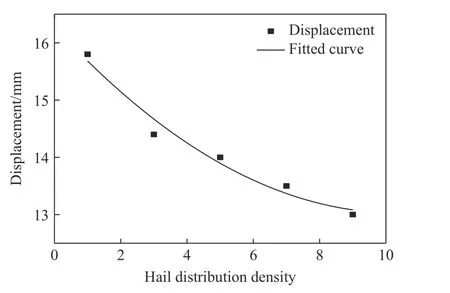
图9 不同冰雹分布密度下双螺旋仿生结构等效撞击中心的最大位移Fig. 9 Center displacement in the equivalent impact domain of double-helicoidal bionic structure under different hail distribution densities
3 结 论
对冰雹撞击下腔棘鱼鳞双螺旋仿生结构的力学响应进行了数值模拟研究,得到以下结论。
(1) 双螺旋仿生结构在冰雹作用下的毁伤程度低于相同密度下的正交层合结构。冰雹撞击能量增至1 149.3 J 时,正交层合结构的撞击区域出现明显的基体破碎和纤维断裂,而双螺旋仿生结构仅表现为撞击区域的浅表分层和少量纤维断裂。
(2) 冰雹作用下双螺旋仿生结构的动态响应可分为3 个阶段:随着撞击能量的增加,撞击区域首先发生基体拉伸,撞击点临近区域发生分层及面外凸起;随后,分层区域向四周扩展,在冰雹的持续加载下撞击位置的位移达到最大值;最后,双螺旋仿生结构出现回弹直至稳定。
(3) 冰雹载荷下双螺旋仿生结构的接触力峰值出现在撞击点达到最大位移之前,且其能量吸收比和接触力峰值均随撞击能量的增加而线性增大。在相同质量冰雹的作用下,随着冰雹分布密度的增大,双螺旋仿生结构上表面的损伤程度逐渐减小,下表面损伤区域逐渐增大。
研究结果可为腔棘鱼鳞仿生结构在冰雹载荷下的轻量化设计提供参考。

