乳化炸药水下爆炸载荷输出特性实验研究

郑欣颖，李海涛，张 弛，吕岩松

（海军工程大学舰船与海洋学院, 湖北 武汉 430033）

乳化炸药具有良好的抗水性、成本低、安全性好、污染少等优点，广泛应用于民用爆破工程。水下爆破是乳化炸药的重要应用场景。为了更好地服务水下爆破工程，有必要揭示乳化炸药水下爆炸载荷特性，摸清其能量输出特点及规律，从而为水下爆破工程设计提供准确、有力的技术支持。

相比于乳化炸药，TNT 炸药在水下爆炸领域的应用历史更加悠久，积累了很多水下爆炸载荷研究成果[1-3]。因此，人们在研究非理想炸药的水下爆炸能量特性时，经常将其与TNT 炸药进行对比分析，通过TNT 当量系数（在比例距离一定的条件下，当炸药爆炸产生相同的超压峰值、正压冲量或气泡脉动周期时，炸药与TNT 的质量比）来评定乳化炸药的能量特性[4]。乔小玲等[5]、范俊余等[6]、夏曼曼等[7]开展了不同质量的岩石乳化炸药的空中爆炸实验，给出了与实验结果吻合较好的TNT 和岩石乳化炸药空中爆炸压力表达式。赵根等[8]通过水中爆破实验得到了乳化炸药水中爆炸冲击波传播经验公式；汪泉等[9]测试了乳化炸药的水下爆炸参数，得到其爆炸产生的冲击波能与气泡能之比为0.55，总能量与爆热之比约为0.94，该比值反映了乳化炸药的能量输出情况。

本研究采用实验与理论相结合的方法，获取开阔水域下乳化炸药水下爆炸载荷输出特性，对比分析工况参数对冲击波峰值、气泡脉动周期、冲量、气泡脉动压力、冲击波能以及气泡能的影响，提出乳化炸药水下爆炸的TNT 当量关系，研究结果可为乳化炸药水下爆炸相关研究提供重要参考。

1 水下爆炸载荷计算

1.1 一般经验公式

在无限水域中，某点的冲击波压力随时间的变化规律（指数衰减阶段）可近似用指数函数表示[10]

式中：me为装药量（kg），R为爆心距（m）；k、l、α、β 是由实验确定的炸药相关常数。对于TNT 装药，α=1.13，β=0.89，k=52.27 MPa，l=5 768 N·s/m2。

炸药水下爆炸产生爆炸冲击波时，会伴随产生一个被水包围的气体团，即气泡。设h为炸药距水面的距离（m），r0为装药半径（m），则气泡最大半径rmax和脉动周期T可由以下经验公式表示[11]

1.2 载荷输出能量计算

炸药水下爆炸过程中，其爆炸能量主要以冲击波能和气泡能的形式输出，为了掌握乳化炸药的冲击毁伤特性，必须确定其能量输出形式。单位炸药释放的总能量Et可表示为[12]

2 乳化炸药水下爆炸实验

2.1 实验工况

本实验所用的乳化炸药是由湖北凯龙化工集团股份有限公司生产的2 号岩石乳化炸药（由硝酸铵、硝酸钠、水、乳化剂、复合油、玻璃球组成，其质量分数分别为65%～70%、12%～16%、10%、2.5%、4%、2%），呈柱状，每根长30 cm，质量为300 g，根据需要切割炸药，然后团成球状进行实验。如图1 所示，通过吊车悬吊三角钢架，将其置于宽阔水域（深度不低于5 m）水面以下一定深度，防止在实验过程中沉入水底。此三脚架的边长分别为1.0、1.2 和1.5 m，脚杆下端固定炸药和传感器。通过更换脚杆来调整乳化炸药与PCBW138A10 型自由场压力传感器的爆距。表1 给出了具体实验工况。

表1 实验工况Table 1 Experimental cases

图1 实验布局Fig. 1 Experimental arrangement

2.2 实验步骤

(1) 测定水深。实验前，测量并记录水域深度，选择水深5 m 以上的区域作为实验水域。

(2) 标定乳化炸药水下爆炸能量。药量选择10、80、160 g。将乳化炸药固定在三角架的一个脚杆上，其他两个脚杆固定自由场压力传感器，保持炸药与传感器在同一水平高度；通过吊车将三角架置于水面以下一定深度（固定爆深为1.0、1.5 m）。起爆炸药，并采集自由场压力曲线。

(3) 按照设计工况完成所有爆炸实验，记录传感器数据，分析乳化炸药水下爆炸载荷输出特性。

3 实验结果与分析

3.1 水下爆炸载荷及能量分析

3.1.1 水下爆炸压力时程曲线

图2 给出了各实验工况下乳化炸药的水下爆炸压力时程曲线。各工况下，水下爆炸载荷曲线存在多个压力峰值，其中：第1 个峰值是初始冲击波超压值，第2 个峰值是第1 次气泡脉动压力峰值。以工况1 为例，其冲击波超压峰值约为4.7 MPa，气泡脉动压力峰值约为1.0 MPa，时间间隔约为56 ms。比较工况4 和工况6 发现，随着乳化炸药爆炸深度的减小，二次压力即气泡脉动压力峰值出现的时刻不同程度地延后，表明气泡脉动周期增大。比较工况5 和工况6 发现，随着炸药与测点距离的减小，冲击波压力峰值出现明显的陡增，但二次压力峰值出现的时刻却几乎没有明显变化，表明爆距对超压峰值有显著影响，但对气泡脉动周期几乎没有影响。对比所有工况发现，乳化炸药水下爆炸压力时程曲线具有一致的变化规律：水下爆炸发生后，首先冲击波压力快速达到最大值，其峰值压力大，但作用时间短，波形陡峭；随后，爆炸气泡快速膨胀，因自由液面的影响，流场压力在气泡膨胀-收缩的较长时间内出现一定的低压区；随着气泡的收缩，当气泡半径接近最小值时，周围流场压力再次升高，形成压力峰值，即气泡脉动压力峰值，该峰值远低于初始冲击波压力峰值，但持续时间比初始冲击波超压长得多。

图2 不同工况下乳化炸药水下爆炸压力时程曲线Fig. 2 Pressure histories of underwater explosion for the emulsion explosive under different cases

图3 给出了工况1 下乳化炸药水下爆炸压力实验曲线与Geers-Hunter 理论公式[15]计算曲线的对比情况。可见，实验曲线与理论公式计算曲线的变化趋势基本一致，冲击波压力峰值分别为4.7 和6.1 MPa，气泡脉动压力峰值分别为1.0和1.3 MPa，气泡脉动周期分别为56 和48 ms。气泡脉动周期大致吻合，初始冲击波压力峰值与气泡脉动压力峰值存在一定差异。产生这种情况的原因可能是：Geers-Hunter 理论公式是基于球状气泡理论提出的，忽略了边界条件的影响，所计算的水下爆炸气泡载荷是理想的无边界条件下的载荷。本实验存在自由液面的影响，且炸药距离自由液面不远，自由液面为气泡提供常压边界条件；当气泡膨胀至自由液面附近时，受到边界的影响，气泡被拉伸不再呈球状运动，略微延长其运动周期；同时，气泡会发生溃灭和射流，其携带的载荷被耗散至水中，一定程度上削弱了气泡脉动压力。综上所述，通过Geers-Hunter 载荷公式可以预测乳化炸药水下爆炸载荷输出的一般变化规律，特别是气泡脉动周期。

图3 压力的实验曲线与Geers-Hunter 公式计算曲线的对比Fig. 3 Comparison of pressure histories between experiment and Geers-Hunter formula

3.1.2 冲击波超压、气泡脉动周期和冲量

提取各工况下冲击波超压、气泡脉动周期和冲量（冲击波阶段），将其与TNT 当量系数为0.625 的水下爆炸经验公式计算值进行对比，结果见表2。可以看出：爆距越大，相同质量和爆深的乳化炸药水下爆炸的超压峰值越小，冲量越小，但气泡脉动周期保持不变；爆深越大，相同爆距和质量的乳化炸药水下爆炸的气泡脉动周期越小，超压峰值和冲量保持不变，与经验公式得到的变化一致。各工况下的冲击波超压峰值和气泡脉动周期与经验值都比较吻合，平均相对误差分别约为14.2%和12.4%，而冲击波阶段的冲量与经验值的平均相对误差较大，约为24.0%。由于经验公式主要依据大药量（几十千克）实验数据，而本实验属于小药量级（几十至几百克），因此对实验数据分析的实用性和准确性造成一定影响。综上所述，各工况下水下爆炸载荷实验值与经验公式计算值具有较一致的变化规律，表明该乳化炸药的TNT 当量系数取0.625 具有一定的合理性。

表2 实验结果与经验公式计算结果对比Table 2 Comparison between experimental results and empirical formula

3.1.3 气泡脉动压力特性

气泡脉动是水下爆炸的一个重要过程，揭示其压力特性对于掌握整个水下爆炸载荷输出特性具有重要意义。图4 给出了各工况下第1 次气泡脉动阶段压力曲线的局部放大图。从图4(a)中可以看出，工况1 下气泡脉动压力峰值约为0.97 MPa，压力上升沿持续约7.99 ms，压力下降沿持续约1.08 ms。从图4(b)中可以看出，工况2 下气泡脉动压力峰值约为0.69 MPa，压力上升沿约2.43 ms，压力下降沿约0.68 ms。将图4(a)、图4(b)与图2(a)、图2(b)进行比较，可以看出，气泡脉动压力峰值约为初始冲击波压力峰值的10%～20%，持续时间比冲击波作用时间长。对比各工况下的气泡脉动压力曲线后发现：脉动压力波形呈现先缓慢上升达到峰值后急速下降趋于零并保持平稳的态势，波形上升沿耗时普遍比下降沿耗时长。当其他条件相同时，爆距越大，气泡脉动压力峰值越小；爆深越大，气泡脉动压力越小；药包质量越大，气泡脉动压力峰值越大。

图4 不同工况下乳化炸药水下爆炸气泡脉动压力随时间变化曲线Fig. 4 Histories of bubble oscillation pressure for different cases in underwater explosion of the emulsion explosive

3.1.4 冲击波能和气泡能

水下爆炸能量输出包括冲击波能和气泡能两方面，可以用µEs/Eb反映能量输出结构。根据式(9)、式(10)和式(11)，得出不同工况下乳化炸药水下爆炸的能量输出参数，如表3 所示。

表3 乳化炸药的能量输出结构Table 3 Energy structure of emulsion explosive

通过实验数据可以看出，不同爆距和埋深处的气泡能相对稳定，冲击波能随爆距的增加而减小，随炸药埋深变化而几乎保持不变。不同种炸药的冲击波能和气泡能不同，同种炸药在不同工况下的冲击波能和气泡能几乎相同[16-18]。各工况下，该乳化炸药水下爆炸冲击波能的平均值为0.883 kJ/g，气泡能的平均值为2.417 kJ/g，故µEs/Eb的平均值为0.497，总能量的平均值为3.617 kJ/g。结合图2 可以看出，气泡脉动压力峰值只占冲击波压力峰值的10%～20%，气泡能却是冲击波能的2 倍左右，所以气泡脉动的能量输出对结构的爆炸损伤作用不容忽视。

3.2 乳化炸药的TNT 当量系数计算

3.2.1 等超压下的TNT 当量系数

参考Cole[19]的冲击波峰值压力经验公式，基于超压峰值实验数据，按式(3)拟合乳化炸药水下爆炸的冲击波超压表达式。采用最小二乘法，得到

拟合结果的相关系数为0.917，残差平方和为10.722。图5 给出了乳化炸药水下爆炸超压峰值-比例距离拟合曲线。可以看出：乳化炸药水下爆炸冲击波超压峰值随着比例距离的增大而减小，变化趋势近似为指数型曲线；当比例距离小于4 时，冲击波峰值压力下降得较快，当比例距离大于4 时，冲击波峰值压力的下降趋势变得平缓。

图5 超压峰值与比例距离的拟合曲线Fig. 5 Fitting curve between peak overpressure and scaled distance

根据Cole[19]关于水下爆炸冲击波超压峰值的经验公式可知，乳化炸药的TNT 当量系数W可表示为

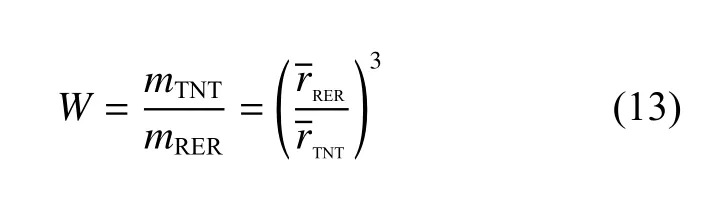
式中：下标TNT 和RER 分别代表TNT 和乳化炸药。

3.2.2 等气泡脉动周期下的TNT 当量系数

同样地，按式(8)对乳化炸药水下爆炸的气泡脉动周期进行拟合，采用最小二乘法，得到

图6 气泡脉动周期与比例爆深的拟合曲线Fig. 6 Fitting curve between bubble pulsation period and scaled explosion depth

4 结 论

开展了某乳化炸药水下爆炸实验，得到了该乳化炸药水下爆炸压力时程曲线，分析了水下爆炸能量输出特性，拟合得到等超压和等气泡脉动周期条件下乳化炸药的TNT 当量系数，得到如下主要结论。

(1) 乳化炸药水下爆炸载荷输出特性与TNT水下爆炸载荷类似，TNT 当量系数为0.625；利用Geers-Hunter 理论公式可预测乳化炸药水下爆炸载荷的一般规律，特别是气泡脉动周期。

(2) 乳化炸药水下爆炸气泡脉动压力峰值约为初始冲击波压力峰值的10%～20%，且持续时间比冲击波作用时间长；气泡脉动阶段的压力曲线呈先缓慢上升后急速下降的趋势，波形上升沿耗时比下降沿耗时长。

(3) 该乳化炸药的水下爆炸输出能量中，气泡能约为冲击波能的2 倍，气泡脉动产生的能量对结构的爆炸冲击损伤作用不容忽视。

(4) 在本实验条件下，乳化炸药水下爆炸等超压和等气泡脉动周期的TNT 当量系数略有不同，当比例距离为2.210～6.962 m/kg1/3时，该乳化炸药的TNT 当量系数平均值分别为0.595 和0.646。