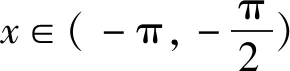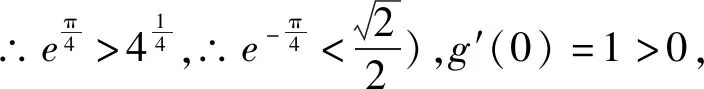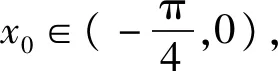例谈三角函数问题求解中的设而不求

甘肃省灵台县第一中学 (744000) 王海燕

设而不求是一种重要的数学思想方法，在三角函数问题中常结合设而不求的方法来解决问题.

1.三角函数求值中的设而不求

对于三角函数sinx,cosx与tanx的求值，充分利用三角函数基本关系式，和角公式、倍角公式进行三角恒等变形，要优先考虑用已知角表示所求角，从而使解题过程得到优化．

例1 计算(1) sin10°sin30°sin50°sin70°；

(2)sin220°+cos250°+sin20°cos50°.

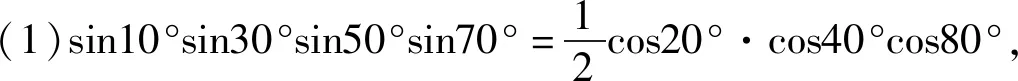
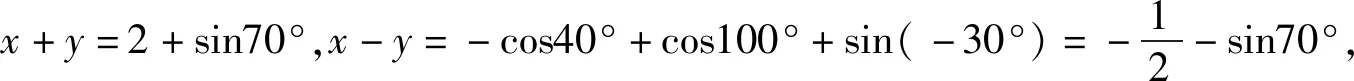
评注：本题设了对偶式，根据对偶的两个式子的和、差，积求得关系，进而求解.

2.三角函数周期中的设而不求

三角函数的周期体现了三角函数值重复出现时自变量的间隔，对于函数f(x)=Asin(ωx+φ)，其周期是由ω决定的，ω大小决定着函数图象伸缩的幅度．

评注：本题中结合了三角函数的周期性，将满足题设条件的所有x1,x2可能取值整体表示了出来，此解法引入了整数元k和m有利于简化解题过程．

3. 三角函数对称性中的设而不求

对于一般的三角函数f(x)=Asin(ωx+φ)，既具备周期性，其图象也具备对称性，二者密切关联．函数的半周期是两相邻对称轴间的距离，函数所有零点是对称中心的横坐标，相邻零点的距离也是半周期．因此∀x1,x2∈R，若函数f(x)=Asin(ωx+φ)的图象关于直线x=a对称，则x1+x2=2a的充要条件是f(x1)=f(x2)；若f(x)=Asin(ωx+φ)的图象关于点(a,0)中心对称，则x1+x2=2a的充要条件是f(x1)+f(x2)=0．

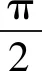
(1)求函数f(x)的解析式，并求其图象的对称轴方程；

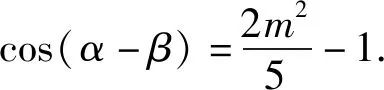
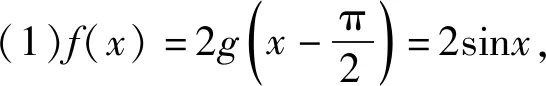
评注：依据对称性可知α+β为定值，α与β的间距恰好是β(或α)与对称轴的间距的2倍，对目标恒等变形之后，抓住方程的根满足方程适时代换，设而不求，从而解决问题．

4.变量整体代换中设而不求

在解决许多三角函数问题时，需从全局着眼审视各个量之间的来龙去脉，寻觅各变量之间的联系，整体把握问题命脉，通过设而不求，整体代换，实现整体解题．

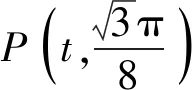
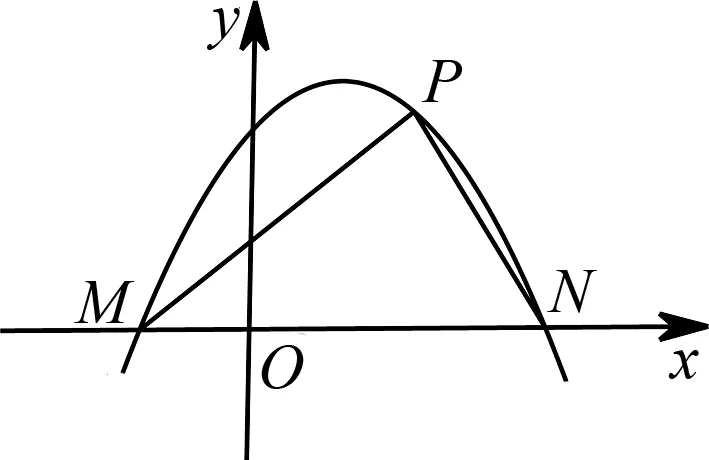
图1

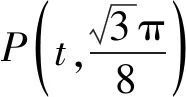
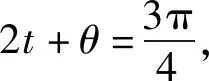
5.解三角形中设而不求

例5 已知直线li:3x-4y+ai=0，其中ai是公差为5的等差数列{an}的第i项.在直角△ABC中，∠ABC=90°，A∈l1,B∈l3,C∈l4，求△ABC面积的最小值．

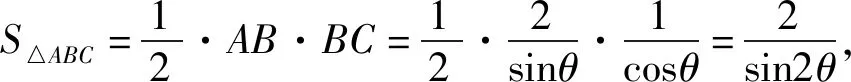
图2

评注：本题设出∠ABD后，把三角形△ABC的面积用∠ABD的三角函数表示出是解题的关键.

6.三角函数求导中设而不求

例6 已知函数f(x)=eax-sinx-1，曲线y=f(x)在x=0处的切线方程为y=b.求函数f(x)在(-π,0)零点的个数.