重本质形成解题思路 探结构确定解题策略——以解析几何中“两根不对称”问题的求解为例

北京市第八十中学 (100102) 孙世林 李 丁

解析几何的知识本质是用代数的方法研究几何问题，所以代数运算是解决解析几何问题无法回避的重要环节，在这个环节中根与系数的关系经常使用，但有时会出现x1+x2与x1·x2“结构不对称”情形，使得无法直接应用根与系数关系进行求解，本文以一道模拟试题为例谈谈这种问题的解题思路与策略.

一、试题再现

(Ⅰ)求椭圆C的方程和离心率；

(Ⅱ)过点P(4,0)且与x轴不重合的直线l与椭圆C交于A，B两点，与直线x=1交于点Q，点M满足MP⊥x轴，MB∥x轴，试求直线MA的斜率与直线MQ的斜率的比值．

二、解法探究

1.重知识本质形成解题思路

解析几何较平面几何最大的优势是将运动变化用坐标来表示，实现用代数方法研究几何问题，用代数方法探究运动变化的几何图形中某些不变的性质和规律.本题是过点P作直线l，随着直线l运动变化，探究随之运动变化的两条直线MA和直线MQ的斜率的比值是定值，依据解析几何的知识本质，我们从直线l入手，设直线l的方程为y=k(x-4)(k≠0)，将直线MA和直线MQ的斜率用直线l的斜率k来表示，通过代数运算得出其斜率的比值为定值.

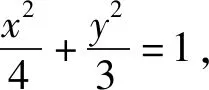
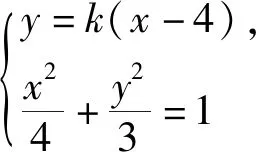
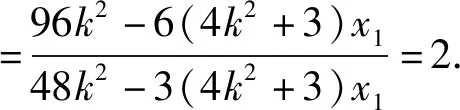
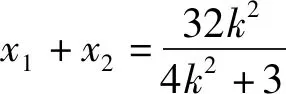
2.探代数式结构确定解题策略

对于解析几何问题即使解题思路清晰但也未必能顺利解决问题，其中代数运算就是拦路虎之一，如本题解题思路清晰，但对两直线的斜率之比的代入、变形、化简是解决问题的关键，解法一中结合代数式的结构我们采取减少变量的方式，将比值化为含有k和x1的形式，在观察比值的结构特征从而求解，可见在解决解析几何问题中，探究代数式的结构特征，实现代数运算的关键，如何探究代数式的结构？我们看下面的解法.

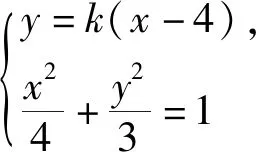
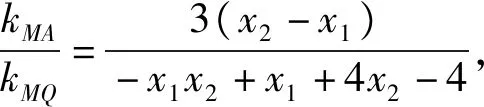
3.揭本溯源探究解法的合理性

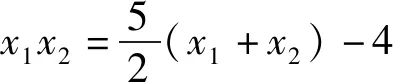
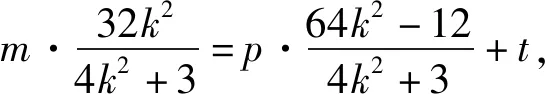
4.多角度探究丰富本题的解法

本题是过点P(4,0)作与x轴不重合的直线l与椭圆C交于A，B两点，求直线MA的斜率与直线MQ的斜率的比值，在解法1解法2都采取从直线方程的点斜式入手，我们也可以采取从直线l方程的横截距式入手，可以使解题过程更简洁.

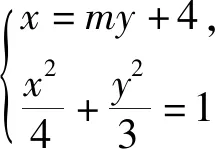
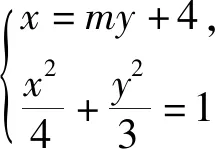
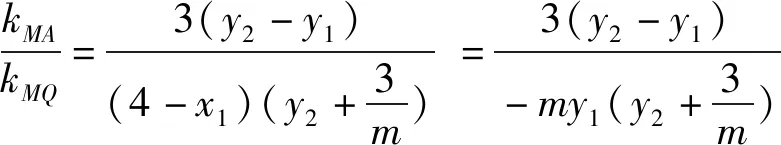
点评：解法3采取了减少变量的方法，借助根与系数的关系将比值用m和y1表示，解法4通过探究y1y2与y1+y2的数量关系，将2my1y2=-3(y1+y2)代入分式实现分子分母结构相同，从而约分得解.

三、反思

《普通高中数学课程标准(2017年版)》明确指出：要注重培养学生的逻辑推理和数学运算素养.要求学生能掌握逻辑推理的基本形式，学会有逻辑地思考问题；要求学生能够在明晰运算对象的基础上，理解运算对象，掌握运算法则，探究运算思路，选择运算方法，设计运算程序，求得运算结果等.解析几何是提升学生数学核心素养的重要载体.解析几何问题的解决往往需要进行复杂的数学运算，为了提升运算能力，解题中要重视解题思路的探究以及运算的策略的分析，优化解题方法，设计运算程序，突破运算中的障碍节点，促进学生数学运算素养真正提升，另外，注意代数运算过程中的算理分析，探究运算规律，分析代数式的结构特征，培养学生在代数式变形中的结构意识，强化观察运算方向的自觉性、强化关注运算结构的简洁性、强化判断运算方法的适合性，从本题的解法探究可以看出，解题中如果能从理解算理和掌握算法的角度去进行解题分析，就能够在解题中发散解题思维，如果能够长期从理解算理和掌握算法的角度思考问题，就能养成良好的思维习惯，最终实现数学运算素养的提升.