一道联赛题的解法探究与反思*

福建省平潭县第三中学 (350400) 薛腊松

厦门大学附属实验中学 (363123) 林运来

竞赛试题是数学题目中的经典力作，大都蕴含丰富的数学思想方法，变化灵巧，精彩迭出.因此，重视对一些典型竞赛题的研究和探讨，实属必要.本文对2021年全国中学生数学奥林匹克竞赛(初赛)暨全国高中数学联赛A2卷第9题的解法进行探究，供大家参考.

一、试题呈现

题目已知△ABC满足AB=1，AC=2，cosB+sinC=1，求BC边的长.

分析：此题是联赛一试解答题的起点题，把三角恒等变换以及正、余弦定理的应用作为考查的重点，考查了分析、推理、计算等关键能力，体现了高中数学教学对三角函数学习的基本要求，有助于学生正确认识三角函数知识的重要性.试题数量关系简洁，计算过程简单，有利于考生稳定发挥.

二、解法探究

思路1 先求三角形内角的函数值，再求三角形边长.

思路2 利用余弦定理直接求三角形边长.

思路3 利用射影定理求解.

思路4 构造直角三角形，利用锐角三角函数求解.

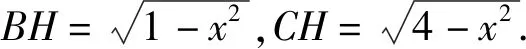
图1

思路5 构造直角三角形，利用勾股定理求解.

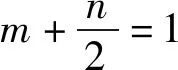
三、解题反思

“三角”一词的希腊文原意是三角形和测量，最初的理解是指解三角形的计算.后来，欧拉引入了三角函数，使三角比(正弦、余弦、正切等)不仅和解三角形有关，而且大大丰富了“三角”的内容.18世纪后，“三角”是被看作包含三角函数和解三角形两部分内容的一门数学的分学科.三角函数在数学和其他学科领域中具有非常广泛的应用，它是中学数学乃至高等数学的重要基础知识之一.

一般地，涉及三角形边角关系类的试题，综合性较强，不仅涉及正弦定理、余弦定理、三角形的几何性质，还会涉及各种三角变换.其常规解法就是利用正(余)弦定理进行边角关系的互化，有时还需利用三角公式进行恒等变形.中学数学的学习中，三角函数的定义或是联系着一个直角三角形，或是联系着一个直角坐标系，或是联系着一个单位圆，总之离不开一个图形，这就为学习“三角”时实现数形结合提供了一条理想的途径.“数形结合”是基本的数学思想之一，正如著名数学家华罗庚所说：“数缺形时少直观，形少数时难入微；数形结合百般好，隔离分家万事休”.对本题而言，相对于常规的解法1、解法2和解法3而言，解法4、解法5通过画图，再利用图形来进行计算和推理，不仅使问题变得形象直观、一目了然，而且极大地减少了运算量，使问题化繁为简，应引起足够的重视.