基于改进气象聚类分型的短期风电功率概率预测方法
吴浩天,孙荣富,廖思阳,柯德平,徐 箭,徐海翔
(1. 武汉大学电气与自动化学院,湖北省武汉市 430072;2. 国网冀北电力有限公司,北京市 100032)
0 引言
截至2020 年底,中国风电总装机容量为280 GW,约为新能源总装机容量的50%[1]。同时,随着以新能源为主体的新型电力系统的构建,风电占比将进一步提升,这也对风电功率预测的准确性提出了更高要求。
风电功率概率预测主要通过区间估计[2-3]或概率密度估计[4]预测得到未来一段时间内风电功率的变化范围。按照建模对象可以将风电功率概率预测分为两大类。第1 类概率预测直接对风电功率进行建模,通过直接挖掘实测数据得到未来一段时间风电功率的概率分布,包括统计法[5-6]与人工智能法[7-9]。该类方法大多存在一定主观因素,例如隶属于统计法的高斯过程回归将风电功率及其影响因素序列视为服从多维高斯分布,然而部分研究表明高斯分布并不适合表征风电功率概率分布[10-11];以文献[7]为代表的机器学习法大多需要依据评价指标构造目标函数,但人为设定的指标与概率预测结果的鲁棒性并不能画等号。
第2 类概率预测以点预测的结果作为基础,统计预测误差并建模得到其对应的概率分布,进而与预测值叠加得到概率预测结果。该类方法能够将先进的点预测与误差建模方法相结合,因而更受青睐。近年来,点预测以深度学习方法为主,包括门控循环单元(GRU)[12]、卷积神经网络(CNN)[13]等。预测误差建模主要分为参数化与非参数化方法。参数化方法假定预测误差遵循某一特定形式的分布,如高斯分布[6]、通用分布[11]。非参数建模利用核密度估计[4]、Cornish-Fisher 级数[14]等方法实现非线性映射,计算出预测误差概率密度函数(probability density function,PDF)或累积分布函数(cumulative distribution function,CDF)的分位点。
引入条件概率理论对相似样本进行聚合划分有助于提升预测准确性。其中,以点预测功率与风速的大小为条件进行样本分类是最常见的条件概率预测方法[15-16]。此外,基于多维气象数据进行天气分型从而实现分组预测的方法得到了广泛应用。文献[17-19]分别依据风速、气温、气压等因素的性质对样本进行相似日分类,组成不同气象模式,实现分组功率预测;文献[20]设计了天气分型因子,并按照晴、雨等气象条件进行光伏预测。然而,由于同日不同时刻的气象条件可能具有一定差异,若按照文献[17-19]的思路以日为单位划分气象模式,将一日中高温与低温、高风速与低风速的样本归为一类,则可能在各模式中引入一定噪声成分。而且,以文献[17-20]为代表的研究主要应用于新能源功率点预测。有关多维气象分型的风电功率条件概率预测,目前尚无足够的理论研究支撑。
基于上述研究,本文提出了基于气象聚类分型与改进高斯混合模型(Gaussian mixture model,GMM)聚类的风电功率概率预测方法。首先,结合最大期望(expectation-maximum,EM)算法与改进的秃鹰搜索(improved bald eagle search,IBES)算法提出基于IBES-EM 算法的GMM(IBES-EMGMM)聚类模型,依据多维气象数据对历史气象-功率数据集聚类划分,得到多个气象模式。其次,利用CNN-GRU 网络对各气象模式的数据集进行训练得到点预测结果,据此统计各气象模式下的误差样本,采用Cornish-Fisher 级数建立各气象模式下风电功率预测误差CDF 分位点,并与对应点预测结果叠加,得到最终的概率预测结果。算例仿真从聚类效果与概率预测角度验证了IBES-EM-GMM 聚类相较于其他聚类模型的优越性。
1 气象聚类分型
短期风电功率概率预测通常以次日00:00 起至未来24~72 h 的气象预报数据作为输入,预测对应时刻风电功率的置信区间或概率分布。本文计及气象四要素(风速、风向、气温、气压)提出IBES-EMGMM 聚类模型。该模型根据历史气象数据的自身性质,将其自适应划分为多个气象模式,继而实现精细化的分组训练与预测,其示意图见附录A 图A1。
1.1 GMM 聚类
GMM 聚类基于多维GMM 来刻画各样本的簇类。多维GMM 由数个多维高斯分布线性叠加得到,二者PDF 如式(1)和式(2)所示。

式中:N为总样本组数;XEM为待优化参数集合;xn为第n组气象样本。该优化问题常用基于拉格朗日乘子的EM 算法[21]进行求解。
1.2 IBES 算法
秃鹰搜索(bald eagle search,BES)算法每轮迭代的核心寻优部分主要包括选择空间、搜索猎物、俯冲捕猎3 个阶段[22]。选择空间与俯冲捕猎作为一轮迭代的起止阶段,若种群陷入局部最优,则将影响到整体的种群寻优过程。因此,分别利用Levy 飞行与自适应t分布变异策略改进上述两阶段,如式(4)—式(6)所示。式(4)为Levy 步长计算式,式(5)和式(6)分别为改进后的选择空间及自适应t分布变异过程。
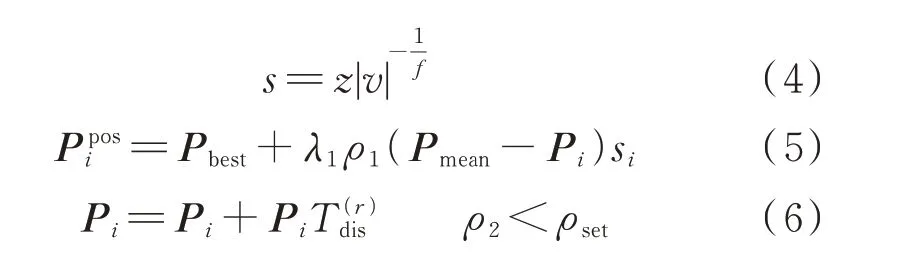

由式(5)可知,在选择空间阶段,当λ1ρ1取值较小时,秃鹰种群易陷入局部最优。因此,引入有较高概率出现大步长的Levy 步长si以拓宽秃鹰的搜索空间[23]。式(6)所示自适应t分布变异以算法迭代次数作为t分布自由度参数,迭代前期自由度小,类似柯西分布,步长较大,从而增强算法前期的全局搜索能力;迭代后期自由度大,类似高斯分布,步长适中,从而提升算法局部收敛能力。
基于Levy 飞行与自适应t分布变异策略改进的IBES 算法流程见附录A 图A2(a)。相较于原BES算法,其在迭代初期具有更大的搜索空间,在迭代后期通过自适应变异提升收敛性能,从而得到更优的聚类结果。
1.3 IBES-EM-GMM 聚类
由于初值随机给定,EM 算法易陷入局部最优,而直接利用IBES 算法求解GMM 聚类无法充分利用目标函数的梯度信息。此外,利用IBES 算法得到的秃鹰位置难以符合GMM 的参数特性,如协方差矩阵θk必须为对称正定阵等。基于两类算法的


步骤3:EM 算法更新。随机选择一只秃鹰,利用EM 算法迭代一步,更新其对应的GMM 参数与秃鹰位置。
步骤4:IBES 算法更新。利用IBES 算法中改进的选择空间、搜索猎物、俯冲捕猎、自适应t分布变异4 个阶段更新秃鹰位置。每个阶段位置更新结束后,需要对秃鹰位置进行边界检查,若某一维位置不在取值范围内,则对该位置随机赋予边界内的值。此外,为了保证GMM 系数αk对应的秃鹰位置分量满足和为1 的约束,在边界检查结束后需要对该分量按照式(8)进行标准化操作。
步骤5:终止条件。IBES-EM 算法终止条件为指定迭代数Nset内最佳适应度Fbest与平均适应度Fmean的变化值均小于阈值,如式(9)所示。

求得XIBESEM后,遍历所有样本xn,按照式(11)计算xn中第k个高斯分布生成的后验概率γn,k,并将xn归于概率最大的一类,得到气象聚类分型结果。
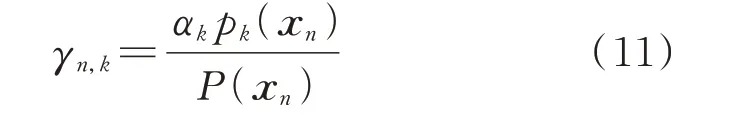
2 基于气象聚类分型的概率预测方法
2.1 CNN-GRU 网络模型
本文采用CNN-GRU 网络[13-14]作为各气象模式下风电功率点预测回归模型,其网络结构和输入输出数据结构如图1 所示。为了保证CNN 对输入特征提取的便捷性,以当前时刻与前3 个时刻的气象四要素组成的4×4 二维特征图作为输入,输出当前时刻的风电功率预测值。这样,基于气象聚类分型的点预测模型能够同时考虑不同气象模式的差异性与相邻时间断面气象条件的耦合特性,从而进一步提升点预测的精度。
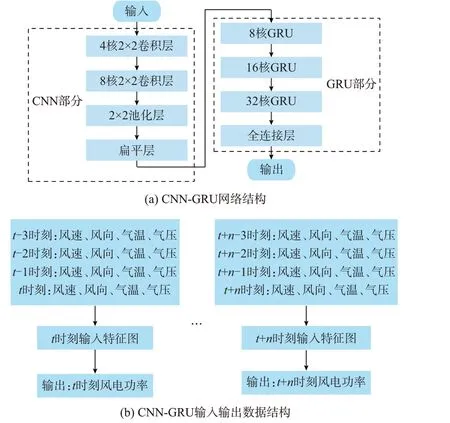
图1 CNN-GRU 网络与数据的结构Fig.1 Structure of CNN-GRU network and data
2.2 预测误差建模
通过CNN-GRU 网络对各气象模式下样本进行训练,可以得到各气象模式对应的预测误差样本,如式(12)所示。

式中:wˉk,j和wk,j分别为第k类气象模式中第j个样本的风电功率预测值与实际值;ek,j为第k类气象模式中第j个样本的预测误差。
利用含5 阶矩的Cornish-Fisher 级数建立各气象模式下预测误差CDF,如式(13)—式(18)所示。

式中:Jk为第k类气象模式的样本数;ηk和σk分别为第k类气象模式预测误差的均值与标准差;uk,3、uk,4、uk,5分别为第k类气象模式下预测误差的3、4、5 阶原点矩;ξq为标准高斯分布对应概率q的分位点;φk,q和Qk,q分别为标准化与去标准化后第k类气象模式下预测误差CDF 对应概率q的分位点。
Cornish-Fisher 级数通过式(13)—式(16)构造预测误差原点矩,并利用式(17)和式(18)进行级数展开与去标准化计算,得到预测误差CDF 的分位点。其对于呈现明显偏轴特征的非正态分布具有较好的拟合效果,并且能够直接对表征置信区间的预测误差CDF 的分位点进行拟合,相较于核密度估计等方法省略了对CDF 求逆从而间接获得分位点的步骤,操作更为简便。
值得注意的是,通过CNN-GRU 网络训练得到的误差样本既包含气象数据引起的误差,又包含模型计算引起的误差。通过足够次数的重复训练,采用最佳训练精度下的网络参数与误差样本分别作为单点预测与误差建模的依据,可以最大限度地消除网络计算误差,从而进一步提高误差建模的鲁棒性。
2.3 预测方法原理
本文提出的概率预测方法整体框架见图2,简易流程如附录A 图A3 所示。
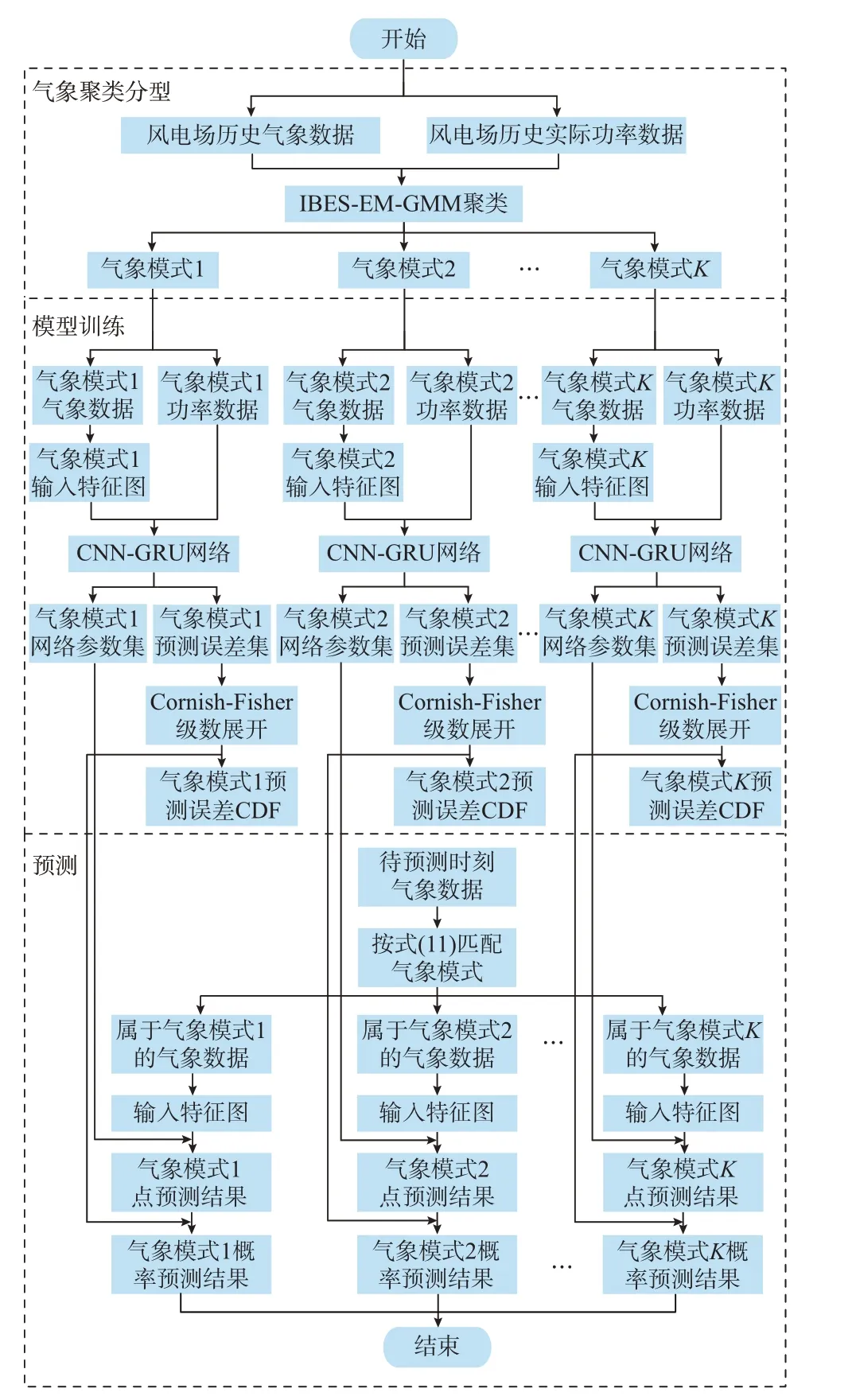
图2 基于气象聚类分型的风电功率概率预测示意图Fig.2 Schematic diagram of probability forecasting for wind power based on meteorological clustering and classification
首先,利用IBES-EM-GMM 聚类将历史气象-功率数据集划分为多个气象模式。其次,构造输入特征图,采用CNN-GRU 网络对各气象模式包含的全部气象-功率数据进行训练,得到训练好的网络参数与预测误差集,并利用Cornish-Fisher 级数得到各气象模式下预测误差CDF 的分位点。最后,输入待预测时刻气象预报数据,按照式(11)计算后验概率匹配气象模式,采用训练好的网络参数集进行预测,得到点预测结果,并将同一气象模式下误差CDF 叠加至点预测结果,得到最终的短期风电功率概率预测结果。
从聚类角度来看,本文所提方法利用IBES-EM算法增强了全局搜索能力,在保证聚类完备性的前提下相较EM 算法能够得到似然值更高、效果更好的气象分型结果。从预测角度来看,由于气象分型考虑了不同气象条件下风电功率及其预测误差的差异性,该方法相比无聚类的概率预测模型更具鲁棒性。
3 算例分析
本章选取中国冀北地区风电场的实际数据进行分析。其中,3.1.1 节至3.3.2 节采用的风电场数据时间跨度为2017 年5 月26 日至2018 年5 月26 日;3.3.3 节采用的风电场数据时间跨度为2016 年5 月28 日至2019 年8 月11 日。其采样间隔均为15 min,包括该风电场的风速、风向、气温、气压预报数据与对应时刻的功率数据。训练集与测试集均按照8∶2的比例进行划分。算例中所有聚类算法最大迭代次数均为100 次,终止阈值γ1与γ2均为0.001。同时,所有智能算法的种群数量均取30,具体参数设置见附录A 表A1。CNN-GRU 网络采用Adam 算法进行训练,其最大训练次数为30 次;最小批处理样本数为总样本数的4%;初始学习率为0.01,20 次训练后学习率为0.004。
算例采用min-max 归一化[12]方法对所有气象数据进行无量纲化处理,以消除不同气象子序列单位不同对预测结果的影响。仿真硬件为Intel Core i5-6400 CPU 与12 GB RAM;软 件 为MATLAB 2020B,其中CNN 与GRU 网络调用MATLAB 深度学习工具箱。
3.1 聚类效果对比
以GMM 为基础的聚类模型通常采用贝叶斯信息准则(Bayesian information criterion,BIC)作为评价指标。其以聚类模型的复杂度作为惩罚项,是反映模型复杂度与似然估计能力的综合指标[24]。BIC值越小,聚类模型的性能越好。
3.1.1 BES 类算法比较
分别采用BES 算法、IBES 算法、BES-EM 算法与IBES-EM 算法优化GMM 聚类模型。以聚类后的气象模式数K(K=2,3,…,20)为变量,计算BIC值进行比较,结果如图3(a)所示。由图3(a)可知,IBES-EM 算法在所有聚类数目下的BIC 值均最小,因此在4 种算法中具有最好的性能。
进一步对比4 种算法在最优聚类数目下的收敛曲线,如图3(b)所示。其中,BES 算法与IBES 算法最优聚类数目均为2,BES-EM 算法与IBES-EM 算法最优聚类数目分别为9 与11。由图3(b)可知,BES-EM 算法与IBES-EM 算法由于利用了目标函数的梯度信息,使得迭代初期的适应度值迅速爬升。同时,由于IBES 算法能够持续拓宽秃鹰种群的搜索空间,其在迭代100 次后的适应度值达到了52 081,相较BES-EM 算法高出了约6 660,论证了IBES-EM 算法具有相对最好的收敛性能。
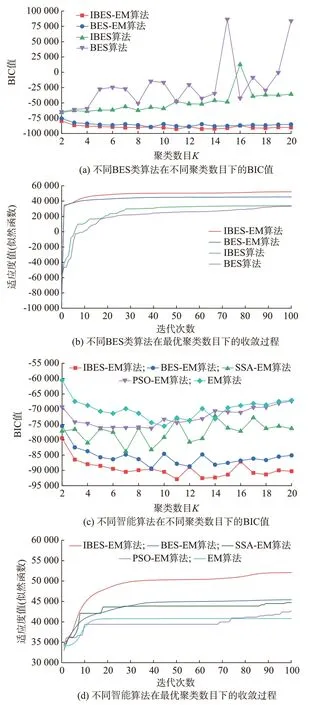
图3 不同算法的BIC 值与收敛过程对比Fig.3 Comparison of BIC values and convergence process of different algorithms
3.1.2 不同智能算法比较
为了验证BES 类算法的优越性,选取粒子群优化(particle swarm optimization,PSO)算法与麻雀搜索算法(sparrow search algorithm,SSA)进行对比。采用相同思路嵌入EM 算法的迭代过程,构成PSOEM 算 法 与SSA-EM 算 法,并 与IBES-EM、BESEM 和EM 算法进行对比,如图3(c)所示。由图3(c)可知,在绝大部分聚类数目下,PSO-EM 与SSAEM 算法的BIC 值高于BES-EM 与IBES-EM 算法,这证明了BES 类算法能够得到更好的聚类结果。
依 据BIC 值 选 取EM、PSO-EM、SSA-EM、BES-EM 与IBES-EM 算法的最优聚类数目分别为10、9、7、9 与11,并绘制最优聚类数目下各算法收敛曲线如图3(d)所示。由图3(d)可知,IBES-EM 算法的似然函数始终处于上升状态,在迭代约9 次后便领先其余算法,收敛性能最佳。
选取IBES-EM-GMM 聚类模型中样本数目较多的7 类气象模式下风速、风向、气温数据的3 维分布进行展示,详见附录A 图A4。在数学层面,各气象模式隶属于不同参数的多元高斯分布;在物理层面,由于气象四要素的数值分布有差异,各气象模式均具有一定物理意义。例如图A4 中,气象模式1 代表中风速、中高气温气象条件;气象模式2 代表中低风速,东南风向(归一化在0.75~1 之间,即270°~360°)气象条件。
3.2 预测效果对比
点预测评价指标选取归一化平均绝对误差eNMAE与均方根误差eNRMSE,概率预测的评价指标选取可靠性[4]、区间平均宽度与技能分数[6],详见附录A。其中,可靠性绝对值越接近于0,则概率预测结果与设定的置信度越契合;区间平均宽度越小,则置信区间聚集不确定性的能力越强;技能分数恒为负值,是对所有置信度下概率预测结果的综合评价,其值越接近于0,代表概率预测结果越好。
3.2.1 单点预测结果对比
基于3.1 节算例分析结果,选取IBES-EMGMM、 BES-EM-GMM、 SSA-EM-GMM、 EMGMM 聚类模型的最佳聚类数目分别为11、9、7、10,利用CNN-GRU 网络对基于4 种聚类模型气象聚类后的训练集以及未进行聚类的原始训练集进行训练,并以15 min 为一个时段进行预测,基于2018 年3 月15 日00:00 至3 月18 日00:00 的 气 象 预 报 数 据进行短期风电功率单点预测。预测曲线对比如图4所示,该时段各模型的预测信息对比如表1 所示。
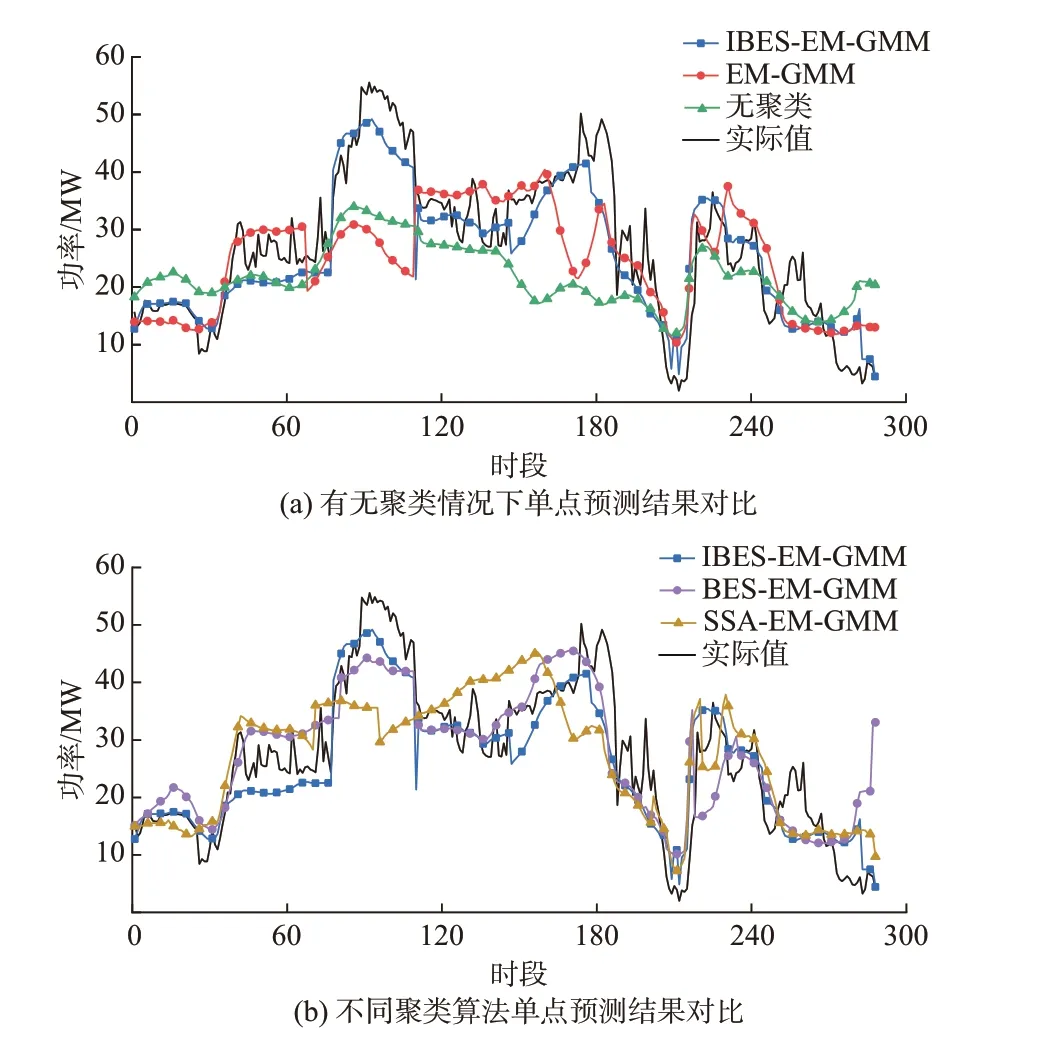
图4 单点预测结果对比Fig.4 Comparison of single-point forecasting results
由表1 可知,该时段下4 种聚类模型均包含多种气象模式,因此该时段的预测效果对比具有一定的代表性。相较于无聚类,4 种聚类模型的点预测精度均有提高,论证了气象分型的有效性。其中,IBES-EM-GMM 聚类模型具有相对最好的点预测效果,其eNMAE与eNRMSE分别为4.52%与5.82%,表明本文所提改进算法的优势。
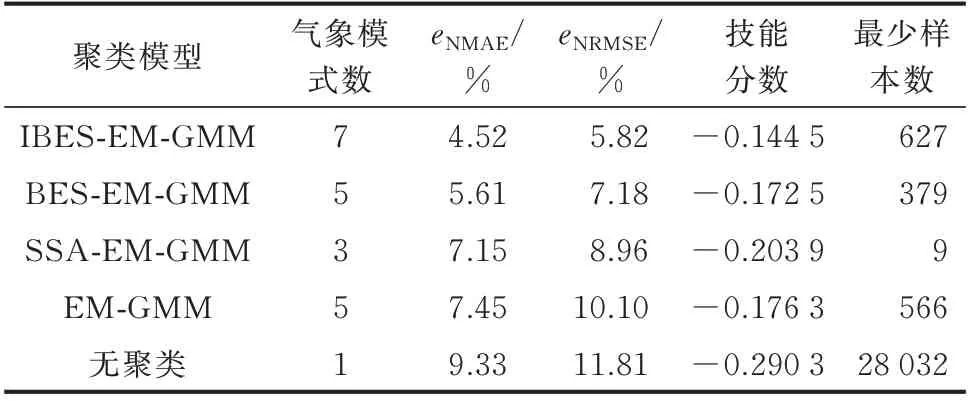
表1 不同聚类模型预测信息对比Table 1 Comparison of forecasting information of different clustering models
如图4(a)所示,在风电功率处于峰谷与拐点阶段,无聚类与EM-GMM 聚类模型的预测误差较大,而IBES-EM-GMM 聚类模型能够在整个时段内准确拟合风电功率的波动趋势。图4(b)中,SSA-EMGMM 聚类模型在时段80 至160 左右的精度远低于其余模型;BES-EM-GMM 聚类模型在最后20 个时段误差较大。综合而言,本文提出的IBES-EMGMM 聚类模型具有最好的点预测效果。然而,在拐点与波动剧烈的时段下,IBES-EM-GMM 聚类模型的精度也有下降。这也表明了单点预测的局限性与通过误差建模进一步修正预测结果的必要性。该时段下每日各聚类模型的预测精度对比见附录B图B1。
3.2.2 概率预测结果对比
选 取80%、85%、90%、95% 置 信 度,利 用Cornish-Fisher 级数对各聚类模型依据气象条件划分后的训练集以及未聚类的原始训练集进行误差建模。不同预测时间尺度下的预测指标对比见附录B表B1,各置信度下的概率预测结果详细对比见图B2。其概率预测指标对比如表1 和图B3 所示。由表1 和图B3 可得以下结论:
1)无聚类的概率预测结果最差;IBES-EMGMM 聚类模型的短期概率预测结果最优;BESEM-GMM 聚类模型对应的技能分数略优于EM 聚类模型,而SSA-EM-GMM 聚类模型的技能分数在4 种聚类模型中最差。这一方面表明气象分型能够有效提升概率预测准确性,另一方面也论证了IBES算法的优势。
2)根据附录B 图B3 可知,无聚类的概率预测结果虽具有可靠性,但区间宽度过大,导致其提供的不确定性信息有限。IBES-EM-GMM 聚类模型利用了相对最窄的置信区间(区间平均宽度不超过25 MW)提供了最可靠(可靠性值在2%以内)的概率预测结果。BES-EM-GMM 聚类模型在可靠性方面优于EM-GMM 聚类模型,但其区间平均宽度相对更宽,因此,二者的效果较为接近。
3)附录B 图B3(a)中,虽然85%与80%置信度下BES-EM-GMM 聚类模型相较IBES-EM-GMM聚类模型的可靠性绝对值更低,但IBES-EM-GMM聚类模型的可靠性值为正,意味着实际预测区间能够囊括比给定置信度更多的实际值。因此,就实际运行而言,IBES-EM-GMM 聚类模型在85% 与80%置信度下的概率预测结果更优。
SSA-EM-GMM 聚类模型在该段时间的预测效果受到了聚类后样本数目的影响。如表1 所示,其样本数最少的模式仅有9 个样本,进而导致其技能分数仅为-0.203 9。不同时间尺度下的预测结果对比见附录B 图B4。
3.3 模型鲁棒性检验
3.3.1 单年样本鲁棒性检验
为进一步验证IBES-EM-GMM 聚类模型概率预测结果的鲁棒性,对各模型的训练集重复训练10 次,并以1 d 96 点为预测单位,对单年样本下测试集共73 d 的风电功率进行10 次预测。评价指标采用eNRMSE与技能分数。其中技能分数的计算选取概率值q=5%,10%,15%,…,95%。各聚类模型评价指标的概率分布如图5 所示,其均值与标准差对比如表2 所示。
由图5 可知,基于BES 算法的两种聚类模型对应指标的概率分布在偏度与峰度上均优于其余所有模型;而IBES-EM-GMM 聚类模型在偏度上略优于BES-EM-GMM 聚类模型。由表2 可知,IBES-EMGMM 聚类模型的eNRMSE为7.58%,技能分数为-0.419 6,分别超过其余模型1% 与0.04 以上;同时,IBES-EM-GMM 聚类模型的eNRMSE与技能分数的标准差均最小。因此,上述结果均表明,IBESEM-GMM 聚类模型的点预测与概率预测结果均具有最强的鲁棒性。各聚类模型区间宽度与可靠性对比见附录C 图C1,IBES-EM-GMM 聚类模型各气象模式与无聚类的预测结果对比详见图C2 和表C1。
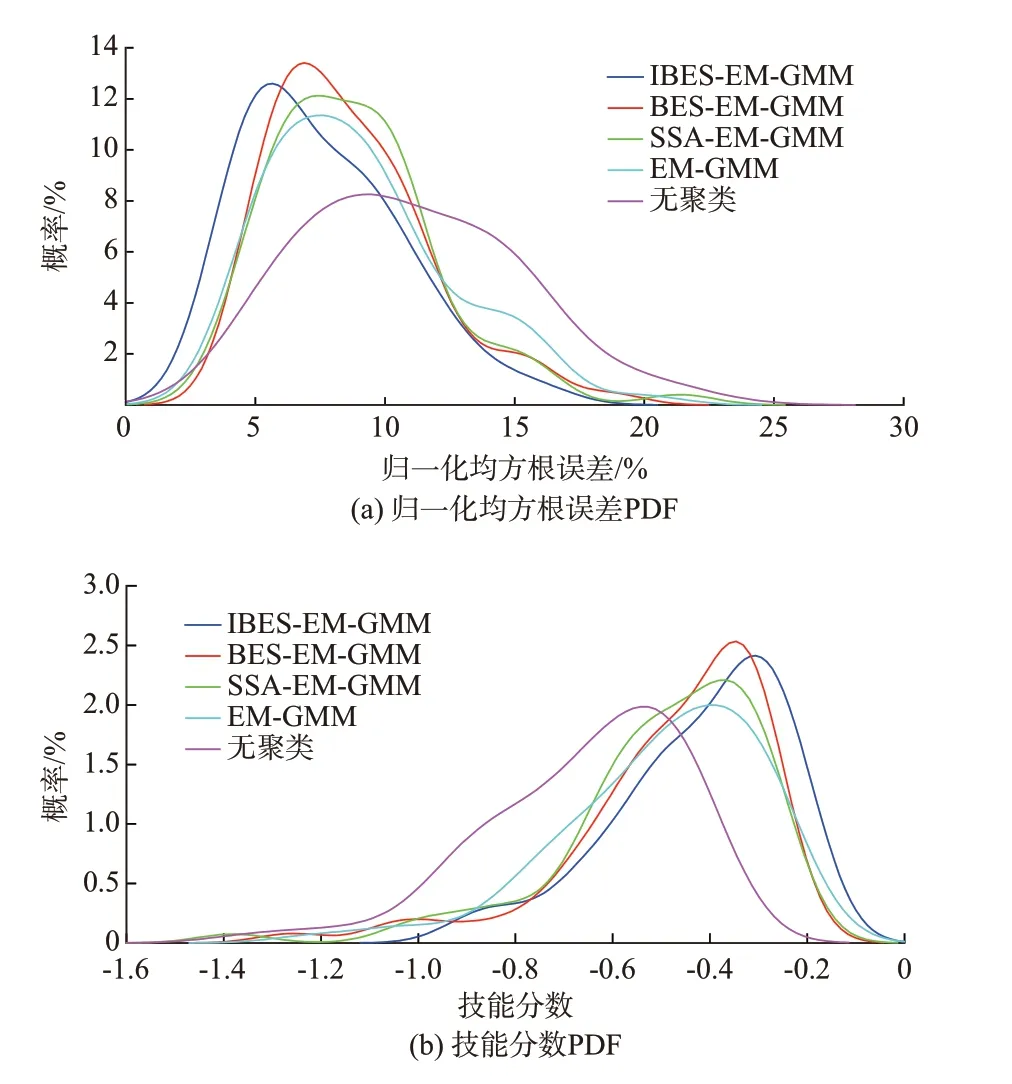
图5 不同聚类模型预测指标的概率分布Fig.5 Probability distribution of forecasting indicators of different clustering models
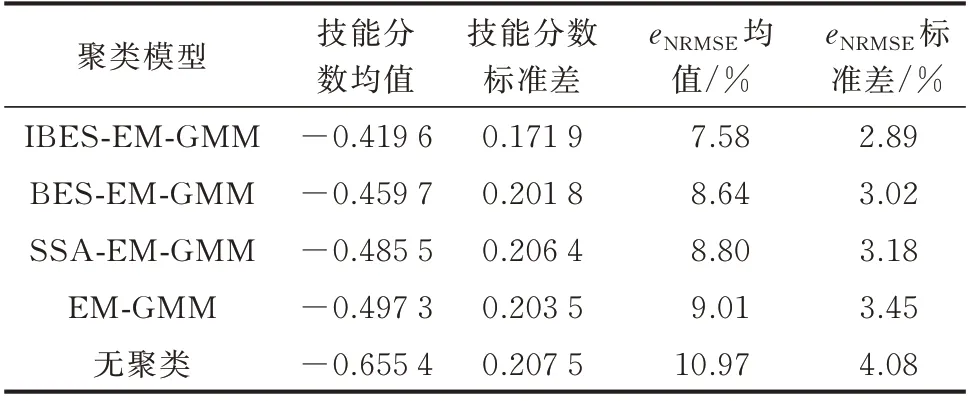
表2 不同聚类模型鲁棒性检验结果对比Table 2 Comparison of robustness test results of different clustering models
在实际应用过程中,当某一气象模式样本数量极少时,重新遍历该模式所有样本,按照式(11)计算各样本归于每类模式的后验概率,并将其合并至后验概率第2 高的气象模式。若合并后某一气象模式样本数仍过少,则重复上述过程将该模式进一步合并,直至所有气象模式包含的样本数量满足预测需求(至少百余条以上)。有关气象模式合并的过程详见附录D。
3.3.2 气象数据误差对聚类模型预测结果的影响
实际预测中,气象预报数据往往存在一定误差。为了进一步分析气象数据误差对聚类模型预测准确性的影响,以单年样本中的气象预报数据为基准,并以预测过程中常见的高斯噪声形式为例,对整个单年样本的气象四要素预报数据叠加如式(19)所示的噪声。

令cnoise分别取0.2、0.5、1、2、5,并将噪声序列叠加至原气象预报数据中,比较IBES-EM-GMM、EM-GMM 聚类模型与无聚类模型对整个测试集的概率预测效果。相关指标的计算与3.3.1 节一致,其结果如表3 所示。
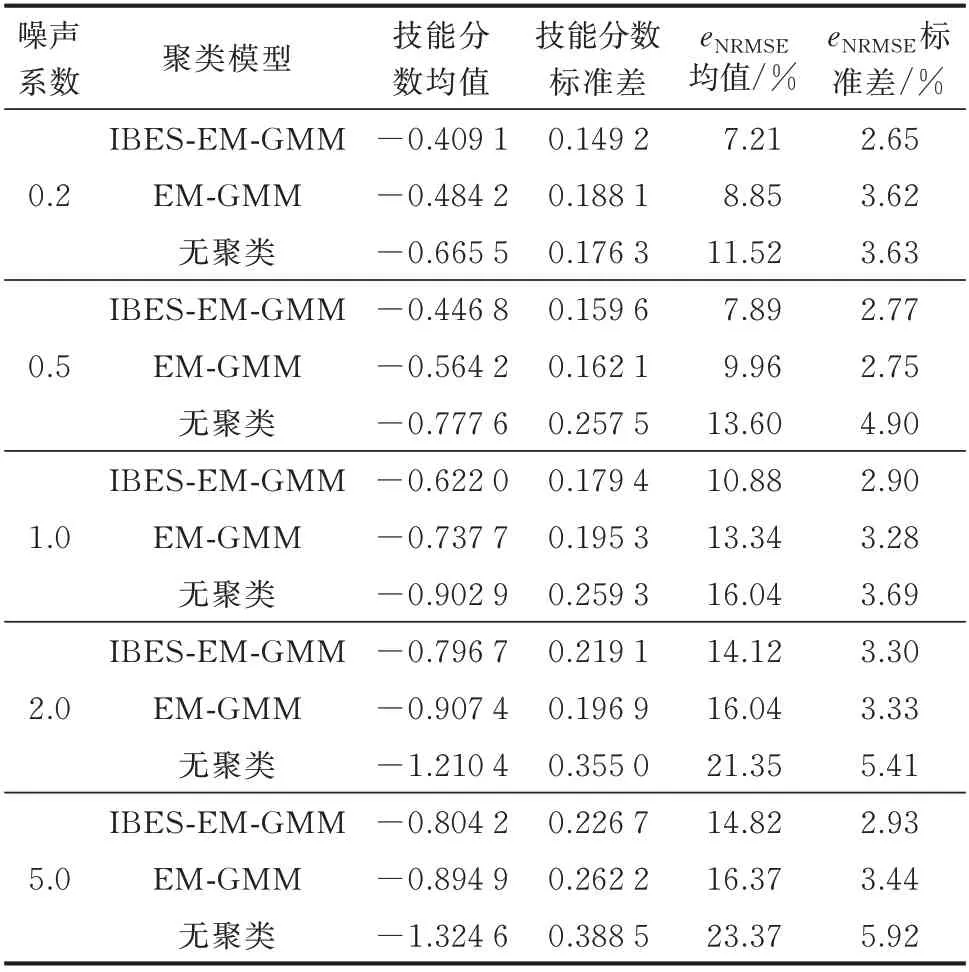
表3 不同噪声系数下不同聚类模型的预测精度Table 3 Forecasting accuracy of different clusteringmodels with different noise coefficients
由表3 可知,在0.2 与0.5 的噪声系数下,由于噪声比例较低,其对于精度影响较小;而当噪声系数达到1 时,各聚类模型的精度均出现了明显的下降;噪声系数超过2 时,预测效果进一步恶化。由于噪声系数超过2 后,输入基本以噪声为主,因此噪声系数为5 时的预测结果精度下降不明显。在不同噪声系数下,IBES-EM-GMM 聚类模型预测效果均最优。同时,在噪声系数不断增大的过程中,IBES-EMGMM 聚类模型预测结果受影响的程度相对最低,且当噪声占据主导的情况下,其技能分数仍达到-0.804 2,分别超过EM-GMM 聚类模型与无聚类模型0.09 与0.5 以上。
IBES-EM-GMM 聚类模型之所以能够在误差影响下保证鲁棒性,是因为其在对含误差的气象数据进行聚类的过程中,一方面对不同气象条件下的数据进行了聚类划分,另一方面也对不同误差条件下的数据进行了恰当划分,因而便于数据驱动类预测模型进行“学习”。
3.3.3 3 年样本鲁棒性检验
本节对3 年样本进行算例仿真,以进一步论证IBES-EM-GMM 聚类模型在聚合更多气象的大样本下概率预测结果的鲁棒性。同样以96 个时段为预测单位,对测试集共234 d 的风电功率进行10 次预测,得到2 340 条评价指标序列,其均值与标准差对比如表4 所示。
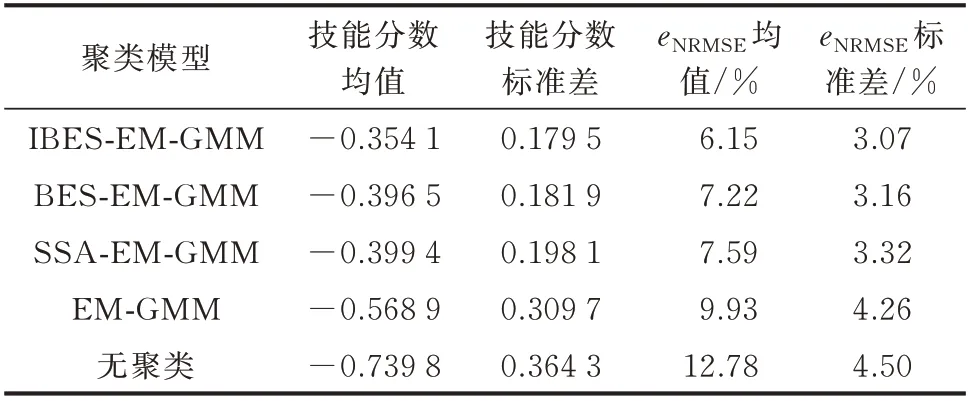
表4 大样本下不同聚类模型鲁棒性检验结果对比Table 4 Comparison of robustness test results of different clustering models with large sample number
在聚合更多气象条件的大样本下,气象聚类后的预测结果精度提升显著。其中IBES-EM-GMM聚类模型的eNRMSE达到6.15%,技能分数为-0.354 1,相较无聚类提升了1 倍。此外,采用智能算法改进后的聚类模型相较于EM-GMM 聚类模型的预测效果提升同样明显。三者中效果相对较差的SSA-EM-GMM 聚类模型的技能分数相较于EMGMM 聚类模型提升约0.17,而3.3.1 节中,对应技能分数提升仅0.01。上述结果表明,在引入更多气象数据参与聚类训练的情况下,由于样本量更为充足,气象分型对预测结果的提升更为明显。
上述鲁棒性分析结果分别从小样本、气象误差、大样本的角度充分验证了IBES-EM-GMM 聚类模型的鲁棒性与有效性。
4 结语
本文提出一种基于IBES-EM-GMM 聚类的短期风电功率概率预测方法。该方法能够根据气象数据的性质自适应划分多个气象模式,并利用CNNGRU 网络与Cornish-Fisher 级数实现各气象模式的分组训练与预测。通过算例仿真可得出以下结论:
1)基于IBES-EM 算法改进的GMM 聚类模型相较于其余算法具有更好的收敛性能,能够得到相对更优的气象聚类分型结果。
2)相较于不进行气象聚类分型,通过各种气象聚类模型得到的概率预测结果在点预测精度与置信区间可靠度等方面均有显著提升。其中,IBESEM-GMM 聚类模型对应的概率预测结果具有最佳的准确性。
3)当气象预报数据存在一定误差时,IBESEM-GMM 聚类模型仍然能够得到较为精确的概率预测结果;随着样本规模的增大,基于气象分型的预测方法优势更加显著,且IBES-EM-GMM 聚类模型的鲁棒性得到进一步提升。
本文的研究为单风电场的概率预测提供了思路,通过气象聚类分型,能够在常规概率预测模型的基础上进一步提升概率预测的准确性。后续研究工作将致力于进一步细化气象特征,如降水量等,并探究在更多气象特征下IBES-EM-GMM 聚类模型的聚类效果与概率预测的鲁棒性。此外,融合多站点、多类型数据的气象预报修正/空间降尺度策略与基于多风电场联合气象聚类分型的概率预测也将是下一步研究计划关注的重点。
附录见本刊网络版(http://www.aeps-info.com/aeps/ch/index.aspx),扫英文摘要后二维码可以阅读网络全文。

