基于Neo4j 图数据库的配电网供电可靠性计算

蒋 玮，王铭华，陈锦铭，2，刘江东，濮 实，许智祺

（1. 东南大学电气工程学院,江苏省南京市 210096；2. 国网江苏省电力有限公司电力科学研究院,江苏省南京市 211103；3. 国网江苏省电力有限公司扬州供电分公司,江苏省扬州市 225009）

0 引言

随着电网建设的不断推进,电力的稳定供应成为日益被关注的问题之一［1-3］。作为电力输送过程的最后一个环节,研究配电系统供电可靠性是帮助电力公司及时发现配电网薄弱环节、保证电力系统供电质量的重要举措,对提高社会经济效益以及配电系统规划升级改造具有重要的指导作用［4］。

目前,针对配电系统供电可靠性指标的量化方法主要有解析法［5-7］、蒙特卡洛模拟法［8-9］和人工智能算法［10-11］等。但是对配电网供电可靠性分析离不开配电网模型,而上述针对配电网可靠性的研究方法主要停留在不同元件建模方式下的可靠性评估算法上［12-13］,忽视了对配电网原始拓扑模型的溯源和分析,难以兼顾配电网拓扑模型的完整性及供电可靠性计算的高效性。

在配电自动化系统中,主要以关系型数据库和单线图2 种形式来存储配电网的结构。以单线图形式存储的配电网模型虽然可以直观展示配电网的拓扑结构,却无法直接用于供电可靠性分析,必须将其转化成可用于编程分析的数据结构［14-15］。虽然这种转化方式能够完整地体现网络拓扑结构,但是对复杂配电网的转化工作量是巨大的,不适用于大规模配电系统的拓扑描述。而以关系型数据库存储配电网结构的形式在数据检索过程中需要复杂的表格连接操作,极大地限制了可靠性分析过程中数据检索的效率［16］。

在研究配电网拓扑结构的过程中,电网设备之间的联络关系天然具备网络的特征,适合用图来存储信息［17］。图数据库通过图形结构存储数据的方式为描述复杂的配电网模型提供了新的解决方式［18-20］。文献［21］基于Neo4j 图数据库构建了电网的全景数据库,分析了基于图数据库进行电网大数据建模的优势。文献［22］基于图数据库设计了一种电网拓扑分析的框架,并验证了在拓扑搜索等方面应用的性能。文献［23］提出了基于Neo4j 图数据库的电网大数据建模方法,并验证了该建模方法在具体数据检索过程中的有效性。文献［24］提出了一种基于图数据模型的配电网建模方法,通过图数据库将配电网信息直接存储在节点和边上来提供更有效的数据管理方式。

上述研究充分说明了图数据库应用于电力系统信息管理与拓扑结构分析中的优势,但是在配电网供电可靠性分析中,图数据库的优势尚未得到充分的应用。因此,本文提出了一种基于Neo4j 图数据库的配电网供电可靠性计算方法,利用图数据库构建配电网拓扑图模型,并结合图论完成图模型的简化。最后,充分利用图数据库基于双向广度优先搜索机制进行高效最短路径查询的特征,实现了配电网最小路可靠性算法的计算,从而有效解决了传统供电可靠性计算方法中复杂网络简化过程不易在计算机中编程实现、负荷点可靠性计算过程较为繁琐的问题。

1 基于Neo4j 图数据库的配电网图模型

1.1 Neo4j 图数据库

Neo4j 图数据库是一个具有高性能、高可靠性和可扩展的开源图数据库,内置Dijkstra、A*等高性能的图论算法。它包含节点和边2 种基本的数据类型。每个节点代表一个设备,边表示2 个设备之间的关联。节点和边均可包含多种形式的属性［25］。同时,每个节点可设置一个或多个标签,拥有相同标签的节点属于一个分组,而每条边只能设置一种类型,类型相同的边属于同一个集合。

Neo4j 图数据库基于图论搜索算法,提供了一套描述性的Cypher 查询语言,可以不需要编写图形结构的遍历代码就完成对图形存储和效率的查询,主要包括MATCH 语句实现图形匹配、WHERE 语句实现过滤条件、RETURN 语句实现结果返回3 个部分。除此之外,Neo4j 图数据库拥有免索引邻接属性,提供高效的图遍历功能。

1.2 描述配电网拓扑的图模型构建

依据配电网络的电压等级、供电路径和联络关系可以对复杂配电网络进行分级分层处理,将各电压等级的网络分为母线层、馈线层及负荷分支层［5］。中国某10 kV 电压等级下的多层级配电网络示意图如图1 所示。以断路器元件为划分条件,本文定义与母线层通过母线断路器相连的馈线为主馈线,把与主馈线相连但是不与母线相连的馈线定义为二级馈线,以此类推,而各负荷分支沿途分布在各级馈线上,其中的配电变压器简称为配变。

图1 中国某10 kV 电压等级多层级配电网络示意图Fig.1 Schematic diagram of a multi-layer distribution network at 10 kV voltage level in China

配电网拓扑结构数据一般以关系模型的形式存储在关系型数据库,不同类型的设备存储在各自的元件表中,设备之间的连接关系存储在连接表中。为了构建基于图数据库的配电网图模型,需要将关系模型对应地映射为G（V,E）结构的图形网络模型,其中,V为节点集合,E为边集合。传统配电网关系型模型的元件和元件间的连接关系就可等效为图形模型中的节点和边。

由于Neo4j 图数据库查询语言对节点查询的效率较对边的查询效率高［26］,因此,本文提出将配网拓扑中所有元件均表示为图数据库中的节点,而元件之间的连接关系则用图数据库中的边表示,对应的关系模型到图模型的映射原则见附录A 表A1。

基于图数据库的配电网图模型如图2 所示。图2 为图1 所示的配电网结构在图数据库中的图模型形式,其中,通过设置节点的标签来区别不同类型的设备,各设备的名称存储在节点的属性当中。例如假设在图模型中标签为CB 的节点代表断路器类型的设备,那么图1 中的断路器元件CB1′就以标签为CB,名称属性为CB1 的节点形式表示。同时,为了进一步提高可靠性分析时对配电网拓扑的查询效率,充分利用Neo4j 图数据库中边具有类型的特征来描述多层级配电网络中的不同等级的馈线层及负荷分支中各元件的连接关系（例如图1 中一级馈线层中的设备）,在图模型中节点就采用“等级1”类型的边进行连接。图1 中负荷分支上的设备在图模型中的节点就采用类型为“负荷等级”的边进行连接。

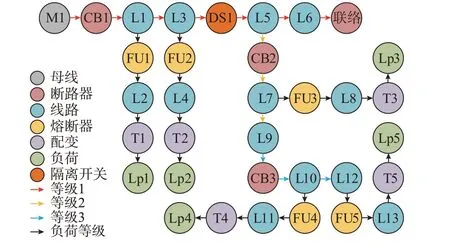
图2 基于图数据库的配电网图模型Fig.2 Diagram model of distribution network based on graph database

对比于配电网关系模型,基于Neo4j 图数据库的图模型在进行供电可靠性分析时的主要优势如下:

1）拥有更为灵活的数据结构和更为自然的数据建模方式。图数据库以节点和边的形式存储配电网拓扑结构信息,可直观展示元件之间的连接关系；而基于关系型数据库的配电网模型则需要创建多个元件表以及存储元件之间连接关系的连接表,极大地限制了信息检索的速度；

2）自带查询语言,提供快速查询与分析功能。对配电网的拓扑数据进行拓扑搜索分析及设备连通分析是进行配电网可靠性计算的基础,Neo4j 图数据库将最短路径算法与自身的存储特性结合起来,通过提供最短路径Cypher 查询语句解决该算法编写的问题；而在关系型数据库中,若要实现最短路径等图算法,则需要编写相关程序,而程序必然会创建大量的相邻数组或矩阵,占用内存和存储空间。

2 基于子图简化的配电网可靠性计算模型

2.1 面向可靠性计算的配电网图模型简化原则

在配电网中,开关设备的安装位置对整个系统的可靠性有着重要的作用,在不考虑备用电源和转供线路约束的情况下,配电网中受故障影响的范围和可恢复供电的范围都只受开关设备的状态决定［2］。因此,为了分析各元件故障时开关设备动作对整个系统可靠性的影响,以图1 中的多层级配电网为例,列出该网络中的故障状态分析表,见附录A表A2,并从中可以总结出位于同一开关节点后的元件故障产生的影响相同,基于这一思想对配电网图模型进行简化,简化原则如下。

简化原则1:位于同一断路器或隔离开关节点后的线路节点在可靠性逻辑上等效为一个串联系统［26-27］,任一线路发生故障都会导致离该线路最近的断路器动作,因此,可以通过生成一个馈线等效节点来取代这些位于同一开关后的线路节点,减少配电网图模型中的节点数。

简化原则2:位于同一负荷分支上的元件在可靠性逻辑上也是串联关系,负荷分支上任一元件发生故障都会导致其首端的熔断器动作,因此,通过生成对应的负荷分支等效节点来取代该条负荷分支上的所有节点,进一步减少配电网图模型中的节点数。

馈线等效节点定义如下。

定义1:馈线等效节点。节点标签设置为FN,所等效的线路节点名称可保存在该馈线等效节点的属性中。

负荷分支等效节点定义如下。

定义2:负荷分支等效节点。节点标签设置为LN,所等效的负荷分支上的节点名称可保存在该等效节点的属性中。

2.2 图模型子图划分及简化

在Neo4j 图数据库中,连接在一起的一系列节点和边被称为路径［28-29］,表示为P（V,E）。通过设置边类型的过滤条件,可提高路径搜索的效率,其定义如下。

定义3:路径搜索。从指定节点出发,沿着特定边类型遍历,并返回能够到达的所有节点和边。搜索路径的过程不会遍历与边类型不匹配的其余可能路径（即节点和边的可能序列）,因此,具有较高的执行效率,适用于判断在特定边类型中,节点之间是否联通以及对图进行划分子图的操作。

配电网图模型G（V,E）中,如果存在Si（Vi,Ei）,且Vi⊆V,Ei⊆E,则 称 图Si是 图G的 子 图［29］。子图划分的目的是将复杂配电网图模型G划分为多个更小的分量Si,针对每个分量Si进行简化可以提高配电网图模型整体简化的效率。因此,根据复杂配电网络每级馈线以及负荷分支中元件之间边类型的不同,基于路径搜索对不同边类型的匹配可以将一个多层级配电网图模型G划分为馈线子图集合SF以及负荷分支子图集合SL。

式中:SF,i代表馈线子图集合SF中的第i个馈线子图；a为馈线子图总个数；SL,i代表负荷分支子图集合SL中的第i个馈线子图；b为负荷分支子图总个数。

划分子图后的配电网图模型G(V,E)包括馈线子图集合SF以及负荷分支子图集合SL,集合SF和SL中的子图分别采用简化原则1 和简化原则2 进行简化,最后将简化后的子图合并生成一个方便用于可靠性分析的配电网图计算模型Gc(V,E)。原始图模型中的每级馈线层及其所属负荷分支,都可划分为一个馈线子图及若干个负荷分支子图。以图2中的一级馈线层为例,其图模型子图划分及简化的过程如图3 所示,具体步骤如下:

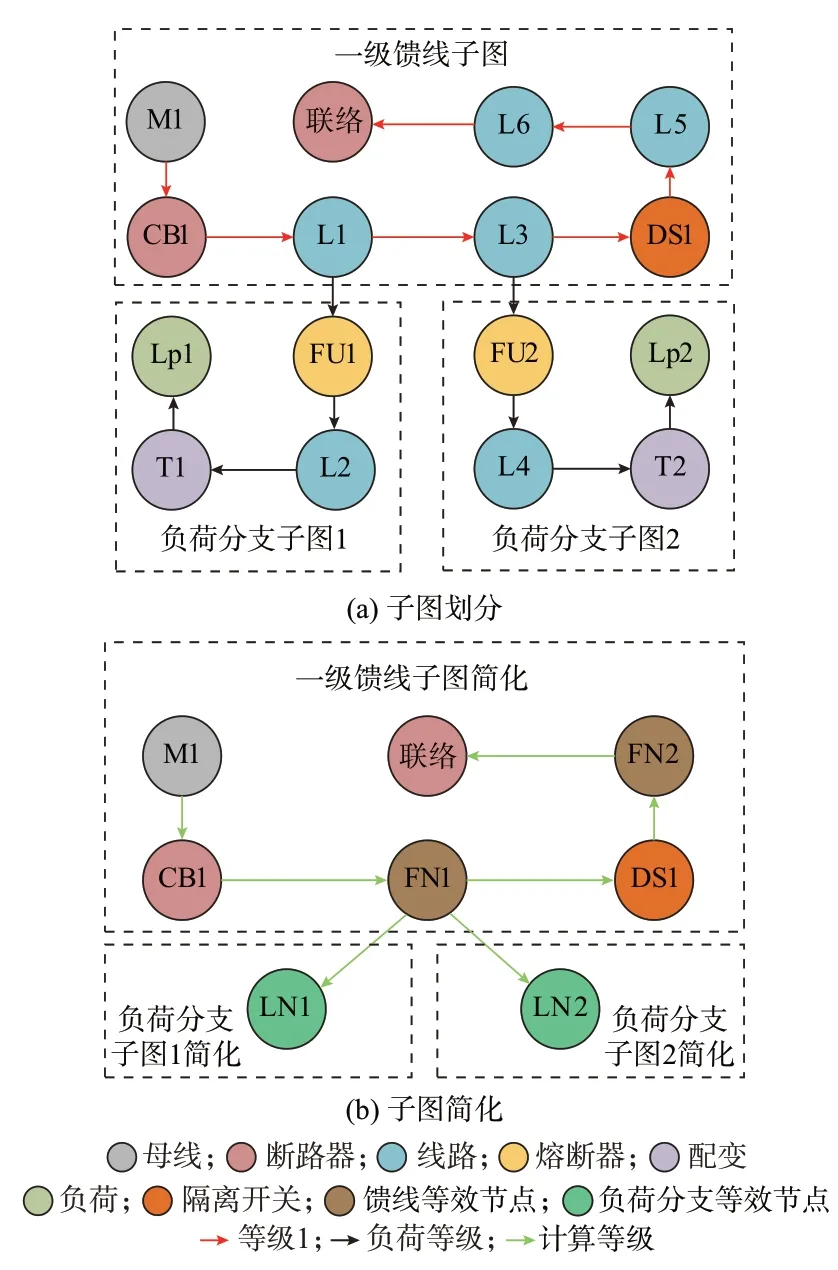
图3 子图划分及简化Fig.3 Subgraph division and simplification

步骤1:进行子图划分。根据一级馈线层中节点之间边类型为“等级1”进行路径搜索,得到SF1（一级馈线子图）。根据负荷分支中边类型为“负荷等级”进行路径搜索,得到SL1（负荷分支子图1）和SL2（负荷分支子图2）,其余馈线层及其负荷分支子图划分同理。

步骤2:进行子图简化。针对一级馈线子图,采用简化原则1 进行简化,通过馈线等效节点FN1 的生成取代线路节点L1、L3,FN2 取代线路节点L5、L6；针对负荷分支子图1,采用简化原则2 进行简化,通过负荷分支等效节点LN1 的生成取代节点FU1、L2、T1、Lp1,负荷分支子图2 同理,简化后的一级馈线层节点数从16 降为7。同时,为了与原始图模型进行区分,简化后的各节点通过“计算等级”类型的边相连接。

基于子图简化的配电网可靠性计算模型Gc(V,E)生成算法伪代码见附录A 表A3,图2基于子图简化后生成的配电网图计算模型见附录A 图A1,在符合可靠性逻辑的基础上有效减少了配电网图模型中的节点数,便于进一步提高可靠性分析的效率。

3 配电网最小路可靠性算法的图计算实现

配电网对负荷的供电可靠性与电源节点到负荷节点的最小路径相关联,当最小路径中任一节点发生故障时,必然会导致该负荷失去供电,此外,还需考虑非最小路径上节点故障时对负荷供电可靠性的影响［8］。因此,本文充分利用Neo4j 图数据库高效率的最短路径查询性能,基于最小路算法对配电网图计算模型进行供电可靠性评估。

3.1 Neo4j 图数据库最短路径查询

在最短路径查询算法中,广度优先搜索（breadth first search,BFS）机制是其中经典搜索算法之一,其类似于树的按层遍历,属于单源最短路径算法。而双向广度优先搜索（double breadth first search,DBFS）以简单广度优先搜索为基础,分别从初始节点与目标节点同时按BFS 方式进行扩展,使之在某个中间状态相遇。相对于广度优先算法来说,由于采用了从两个根开始扩展的方式,搜索树的深度得到了明显的减少,在算法的时间复杂度和空间复杂度上都有较大的优势。

因此,Neo4j 图数据库采用双向广度优先搜索算法来处理最短路径查询的问题,通过首末节点向路径中心均匀同步进行的方式有效提高了对图模型数据的查找效率。

3.2 元件节点的可靠性参数

配电网图模型G(V,E)中,每一类标签的元件节点,都具有对应的故障率参数λ和故障修复时间参数r。而在可靠性计算模型Gc(V,E)中标签类型为FN 的馈线等效节点VFN的可靠性参数表达式为:

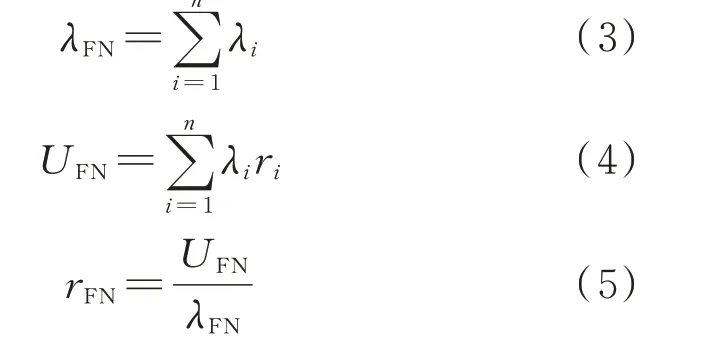
式中:λi和ri分别为节点i的故障率和故障修复时间；n为馈线等效节点VFN所等效的节点数量；λFN、UFN和rFN分别为该馈线等效节点VFN的等效故障率、平均年停电时间及故障修复时间。

同理,标签为LN 的负荷分支等效节点VLN的初始可靠性参数,包括等效故障率λLN、平均年停电时间ULN、故障修复时间rLN,也可根据其元素属性中所包含的各标签节点通过式（3）—式（5）求得。

3.3 基于Neo4j 图数据库查询的最小路可靠性算法

在配电网可靠性图计算模型Gc(V,E)中,每个负荷分支等效节点VLN都连接在对应的馈线等效节点VFN上。由于负荷分支中熔断器的作用,当负荷分支等效节点故障时,不会对馈线等效节点产生影响。因此,可通过最小路可靠性算法先更新各馈线等效节点VFN的可靠性参数,再更新各个负荷分支等效节点VLN的可靠性参数。

3.3.1 馈线等效节点可靠性参数的更新

基于Neo4j 图数据库最短路径查询的最小路算法基本思想为:对于每个馈线等效节点VFN,查询其到电源节点VM的最短路径P(V,E),从而将计算模型Gc(V,E)中的节点分为最小路上的节点和非最小路上的节点2 类。

1）最小路上节点的处理原则:最小路径上任一节点故障都会影响馈线等效节点的供电可靠性,因此,每个节点的故障率和停运时间都参与馈线等效节点的可靠性计算。

2）非最小路上节点的处理原则:查询非最小路上节点故障时所引起动作的断路器节点是否在最小路上,若是,则该节点参与馈线等效节点的可靠性计算；否则不参与。

因此,假设参与某个馈线等效节点x可靠性计算的共有m个节点,其可靠性参数更新如下:

式中:λ'x和U'x分别为馈线等效节点x更新后的故障率和年平均停电时间。

1）当节点k与节点x之间没有分段开关类型的节点时,节点k故障不能被隔离。

2）当有分段开关时,故障可通过操作分段开关进行隔离。此时根据节点k的位置可分为2 种情况。第1 种情况:节点k靠近母线节点侧,在有备用电源的情况下,节点x可通过打开分段开关,联络开关倒闸,由备用电源继续供电,此时,rk取联络开关的倒闸操作时间rc,若无备用电源,rk依旧取节点k设备类型的故障修复时间rk。第2 种情况:当故障节点k远离母线节点侧时,可通过打开分段开关直接隔离故障,此时,rk取分段开关的操作时间rd。

3.3.2 负荷分支等效节点可靠性参数的更新

设负荷分支等效节点y与馈线等效节点x相连接,则更新该负荷分支等效节点的可靠性参数为:

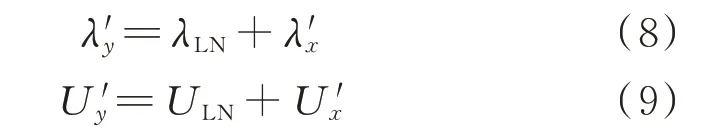
式中:λ'y和U'y分别为节点y更新后的故障率和年平均停电时间。

4 算例分析

4.1 算例及原始数据

以6 节点比林顿可靠性测试系统RBTS（Roy Billinton test system）的馈线为例,进行基于Neo4j图数据库的配电系统可靠性计算。可靠性测试系统结构如图4 所示,该配电系统由106 个设备元件构成,包括30 段线路、23 个熔断器、4 个断路器等。根据断路器所处位置及分级分层原则,该配电系统具有1 条主馈线和3 条二级馈线。

图4 可靠性测试系统结构图Fig.4 Structure diagram of reliability test system

各个类型设备的可靠性参数如表1 所示,其中分段开关的操作时间rd和联络开关的倒闸操作时间rc都取1 h。

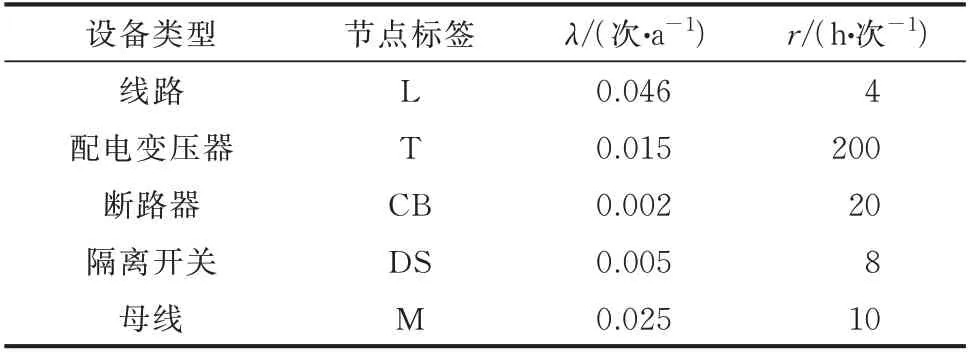
表1 设备的可靠性参数Table 1 Reliability parameters of equipments

基于Neo4j 图数据库的测试系统图模型见附录A 图A2,共有106 个节点。基于子图简化生成的可靠性计算模型见附录A 图A3,简化后的图模型主要由1 个母线节点、6 个开关节点、5 个馈线等效节点FN1～FN5以及23个负荷分支等效节点LN1～LN23组成,共35 个节点,有效减少了图模型中的节点数。

4.2 计算结果及分析

设联络线、熔断器故障率为0,在只考虑一阶故障不考虑二阶故障,以及联络开关与备用电源相连接的情况下,进行测试系统可靠性的分析计算。

4.2.1 各等效节点可靠性指标更新结果

表2 为配电网计算模型中部分等效节点可靠性指标更新前后的结果。其中,FN1～FN5 为各馈线等效节点,LN1～LN23 为部分负荷分支等效节点。更新后的可靠性指标即代表该负荷分支中负荷组（Lp1′～Lp23′）的可靠性程度,所有负荷分支等效节点更新前后的可靠性指标见附录A 表A4。

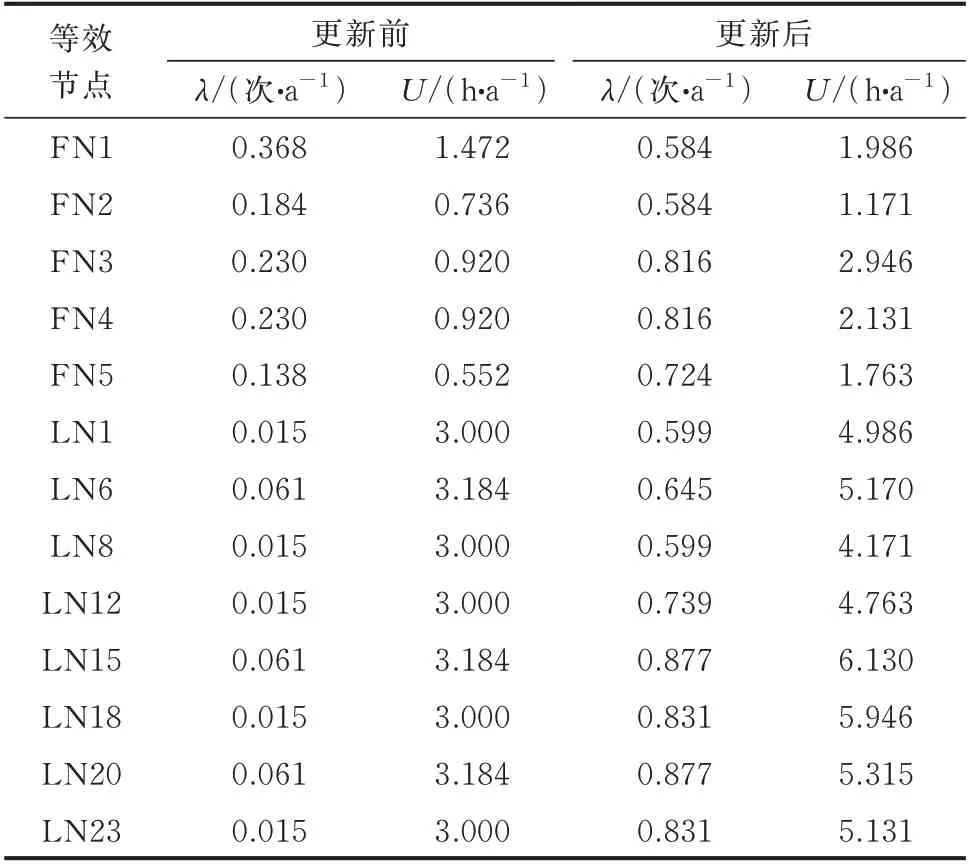
表2 各等效节点可靠性指标更新结果Table 2 Update result of reliability indices of equivalent nodes

4.2.2 基于图数据库的可靠性计算方法性能分析

1）图数据库优势分析

为了验证图数据库为配电网供电可靠性计算方面带来的优势,在存储图4 相同配电网结构数据情况下,对比基于Neo4j 图数据库的配电网图模型和基于关系型数据库MySQL 的关系模型在未简化时采用最小路可靠性算法所需的计算时间。

采用关系型数据库时,需要结合SQL 查询语句和编写对应的单源最短路径搜索算法来实现可靠性计算,以BFS 算法为例,计算时间为18.404 s；采用图数据库时,结合Neo4j 图数据库中基于DBFS 机制的最短路径查询语句实现最小路算法,计算时间为10.370 s。因此,图数据库中的最短路径查询功能能够有效提高对节点遍历的速度,可减少43.6%的计算时间,在计算效率方面有较大提升。

2）计算模型优势分析

为了验证本文基于计算模型的最小路可靠性算法对整体可靠性计算效率的提升,对比了基于原始图模型的传统最小路算法与基于计算模型的本文最小路算法在不同规模配电网下可靠性计算的时间,对比结果如表3 所示。其中,通过在图4 配电网中增加负荷支路的方式来扩大配电网规模。

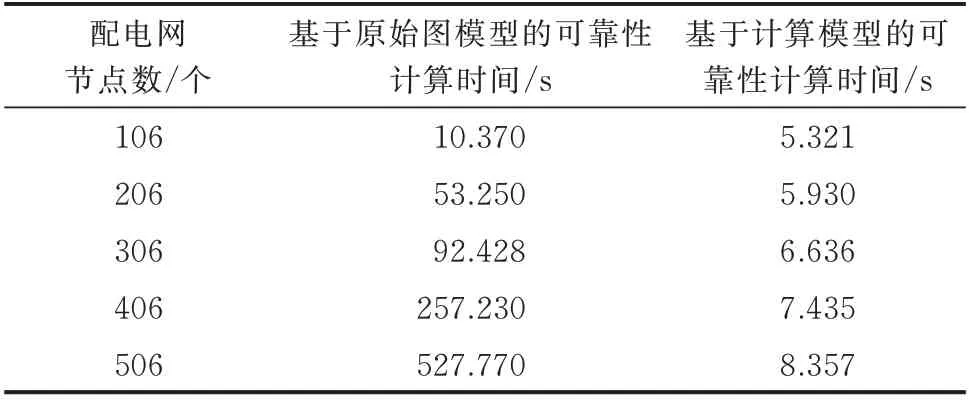
表3 不同规模配电网可靠性计算时间对比Table 3 Comparison of reliability calculation time of distribution networks with different scales

由表3 可知,基于图数据库的配电网图模型虽然能够在一定程度上提高可靠性分析的速度,但是随着配电网规模的增大,图模型节点数的增加会在一定程度上限制节点遍历的速度,其计算时间随节点数的增加呈指数增长。本文基于计算模型的可靠性算法能够有效解决该问题,通过馈线等效节点、负荷分支等效节点的生成,减少了配电网图模型中的节点数,进一步提高了可靠性分析的效率。由此可知,本文基于Neo4j图数据库的配电网供电可靠性计算方法解决了复杂网络简化过程不易在计算机中编程实现的问题,适用于大规模的复杂配电网供电可靠性分析。

4.3 实际配电网算例验证

为了进一步分析本文算法的有效性,选取了中国某10 kV 实际配电网进行算例验证。该配电网由241 个设备元件构成,其结构图、对应的图模型以及简化后的计算模型分别如附录B 图B1、图B2 和图B3 所示,可靠性计算结果见附录B 表B1。

该配电网线路基于传统关系型数据库存储方法的可靠性计算时间为229.412 s,基于本文可靠性算法的计算时间为8.001 s,进一步了验证本文所提方法的有效性。

5 结语

针对目前可靠性计算方法难以兼顾配电网拓扑模型完整性及可靠性计算高效性的问题,本文开展了基于Neo4j 图数据库的配电网供电可靠性计算方法研究,主要工作如下。

1）基于Neo4j 图数据库以节点和边形式高效存储配电系统结构数据的特点,构建了基于图数据库的配电网图模型。

2）充分利用图模型中路径搜索及子图划分的优势,结合可靠性逻辑分析完成复杂配电网图模型的简化,生成便于可靠性分析的图计算模型。

3）将最小路可靠性算法与图数据库最短路径查询相结合,实现了配电网系统的可靠性计算。

算例的结果表明,这种方法将图数据库查询语言嵌套在配电系统可靠性分析的算法中,实现以数据为中心的分析模式,可以使算法更加贴近数据,减少数据交换的时间开销,从而提升配电网供电可靠性计算的效率。本文提出的基于图数据库的配电网图模型及供电可靠性的计算方法对解决含分布式电源的配电网重构等技术难点具有一定的参考价值。下一步,将在现有基础上考虑待转供负荷量、备用电源裕度、分布式电源等因素以提高对配电网供电可靠性分析的合理性。

本文研究得到国网江苏省电力有限公司科技项目(J2020025)的帮助，特此感谢！

本文拓扑数据、图模型转换步骤及计算过程已共享，可在本刊网站支撑数据处下载（http://www.aeps-info.com/aeps/article/abstract/20211031001）。

附录见本刊网络版（http：//www.aeps-info.com/aeps/ch/index.aspx），扫英文摘要后二维码可以阅读网络全文。