计及量测数据丢失的主动配电网电流保护自适应整定方法

余 磊，贾 科，温志文，张 旸，孔繁哲，毕天姝

（新能源电力系统国家重点实验室（华北电力大学）,北京市 102206）

0 引言

配电网结构复杂、拓扑多变,传统三段式电流保护整定配合困难。随着分布式电源大量接入配电网,其多向的“助增”“外汲”电流使得电流保护动作性能进一步劣化［1］。实际配电网中经常采用分布式馈线自动化系统通过智能馈线终端来隔离故障［2-3］,然而分布式馈线自动化系统精确隔离故障仍需依赖电流保护的正确动作及故障信息的准确获取,在配电网多逆变型分布式电源（inverter-interfaced distributed generation,IIDG）接入及网络拓扑频繁变化的情况下,其动作性能有待进一步评估。

近年来,不少学者提出了基于终端量测信息的自适应保护原理,利用多点量测信息提升保护动作性能。然而,部分配电终端（如馈线终端）安装于户外,运行环境较为恶劣,容易受到电磁干扰导致数据丢失或畸变［4］,同时数据在通信通道传输过程中也可能存在数据丢包或误码情况［5］,从而影响保护正确动作。因此,亟待研究可以适应量测数据畸变甚至缺失的配电网自适应电流保护方法。目前,基于通信的配电网自适应保护研究根据自适应调整对象可大致分为两类:自适应调整保护定值和自适应调整保护策略。

自适应调整保护定值的方法所用量测信息包括“故障后”信息和“故障前”信息。基于“故障后”信息的自适应保护利用故障后的量测信息辨识所发生的故障状态及系统运行方式,一般对通信速度要求较高。文献［6］利用主站系统获取的配电网运行状态信息,通过差分进化算法在线计算方向过流保护定值；文献［8］通过故障后检测得到的故障电流正、负序含量信息,确定故障类型,在线切换保护定值的计算方式。基于“故障前”信息的自适应保护利用故障前量测信息实时感知各电源出力状态,并以此进行保护定值的自适应调整。文献［10-11］根据IIDG 低电压穿越控制下故障电流的输出特性,通过迭代法实时计算电流保护定值,以适应IIDG 出力变化。然而,以上自适应电流保护研究忽略了网络拓扑变化对定值整定的影响,难以适应配电网网络拓扑的频繁变化。

自适应调整保护策略和动作时限的方法利用保护获得的区域信息,执行预先设定的判据或条件,完成故障隔离［12-15］。文献［12］基于IEC 61850 通信标准建立了微电网的中央保护单元模型与就地保护单元模型；文献［13］基于就地保护单元的启动与方向判别信息,提出正向、反向和防孤岛反向故障跳闸方案；文献［14］通过保护启动信号和故障方向信息构成区域保护判据,实现了区内故障加速切除,远后备保护动作时间延长的目标。以上所提自适应保护具备一定的冗余性能,可以适应一定程度的量测信息丢失或错误,但在结构复杂、拓扑多变的主动配电网中,本地保护启动信号和方向元件判别信息的准确性均会下降,甚至错误［16-17］,从而影响其保护的正确动作。

针对以上基于通信的自适应保护研究中存在的问题,本文提出了一种考虑量测数据缺失及错误的自适应电流保护方法。该方法利用多点量测信息生成含实时网络拓扑信息的关联阻抗矩阵,并用于短路电流迭代计算中,使得所提自适应电流保护可以适应配电网网络拓扑的动态变化；采用改进的基于Wasserstein 距离的生成式对抗网络（Wasserstein generative adversarial network,WGAN）实现了缺失数据重构与异常数据修正,解决了基于通信的配电网自适应电流保护可能存在的量测数据丢失及错误问题。

1 基于多点量测信息的自适应电流保护

配电网实时拓扑由其静态拓扑和线路开关运行状态所决定［18］。本文利用配电终端上传的多点量测信息生成含实时拓扑信息的母线电压关联矩阵,并用于电流保护的自适应整定计算中。

1.1 母线电压关联阻抗矩阵的生成

研究对象可以抽象为图1 所示的10 kV 配电网,其中LD1 至LD5 为负荷支线,IIDG 接入点上游线路两侧均配置断路器,称其为双开关线路；其余单端电源供电线路称为单开关线路。

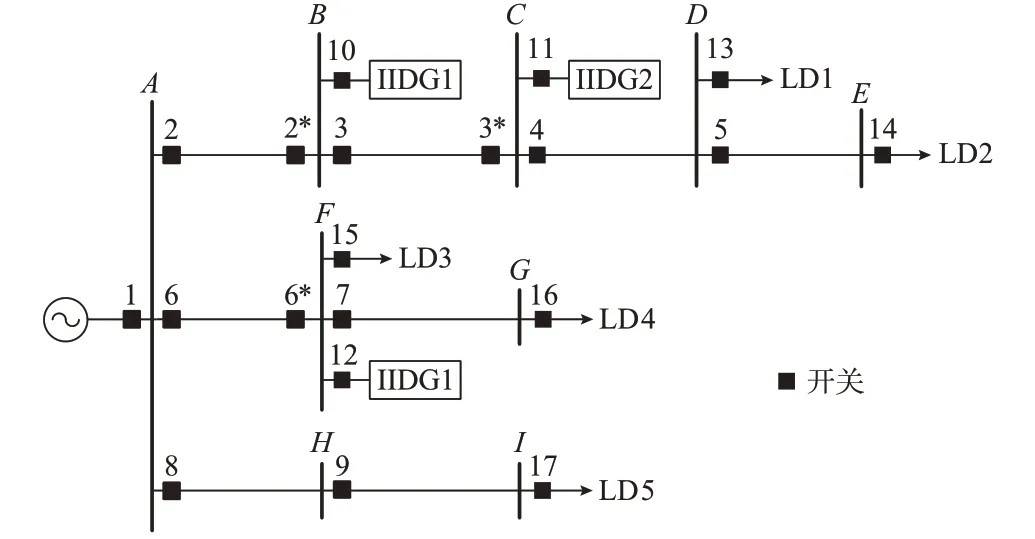
图1 10 kV 配电网结构示意图Fig.1 Schematic diagram of 10 kV distribution network

根据图1 系统母线A的出线情况,可将该配电网分成3 个馈线集（见附录A 图A1 至图A3）,不同馈线集分别用于所对应馈线上电流保护的自适应整定计算。

对于母线i的注入电流与该母线至故障点间线路j流经电流的关系,采用矩阵形式进行描述,形成关联矩阵S,其元素Sij定义为:

通过配电终端监测各开关的闭合状态,闭合时为1,断开时为0；对于双开关线路,均闭合时为1,其余为0。为反映馈线集内开关的上下级关系,依次排列系统电源侧到线路最末端的开关,形成正向开关序列；当馈线集内存在双开关线路时,还需从反方向对开关依次排列,形成反向开关序列。当序列内下级开关状态为0 时,其上级开关状态均为0。

以开关序列值为对角线元素构成对角矩阵C1,将对角矩阵C1乘以关联矩阵S可得实时拓扑描述矩阵TG.i为:

式中:Zj为馈线集内线路j的阻抗。

同理,以各电源开关的闭合状态为对角线元素构成对角矩阵C2,将C2乘以各电源输出电流矩阵可得实时拓扑描述电源电流矩阵IG为:

式 中:İG,i为 母 线i的 实 时 注 入 电 流。

1.2 保护定值自适应整定算法

IIDG 故障电流的精细化求解模型在控制参数未知时往往难以工程应用,基于文献［19］中的IIDG工程实用化U-I映射关系,本文绘制出IIDG 工程实用化U-I映射曲线簇来求取IIDG 的故障电流,详见附录A。在外环控制阶段,本文近似认为其输出功率保持不变,此时短路电流可由故障前的输出有功值与并网点电压d轴分量求得。

保护定值自适应整定前,需要根据静态拓扑信息存储的数据为各线路阻抗、保护所对应的正、反向开关序列以及母线电压关联矩阵；需要终端上送的量测数据为各电源注入电流、线路开关闭合状态及IIDG 输出有功值。

以IIDG 的注入电流作为迭代初始值进行如下迭代:

图1 中各线路的配电终端间隔固定时间（本文取1 min,实际现场中可依据配电网拓扑变化频率、IIDG 日出力曲线等来综合选取）向主站上送遥测、遥信量测信息,主站据此完成保护定值迭代计算,并通过保护通信系统下发给就地安装于配电终端中的电流保护。

2 缺失及异常量测数据的处理算法

受外界环境或通信影响,配电终端上送给主站的量测数据存在缺失、畸变等问题,影响自适应保护定值计算准确性。为此,针对上一章保护算法存在的数据质量问题,提出量测数据缺失及异常的处理算法。

2.1 基于改进WGAN 的缺失量测数据重建

WGAN 在电力系统缺失数据重构中得到了一定应用［21-23］,WGAN 由相互对立的生成器与判别器组成,经博弈双方的决策组合后最终可生成符合原始数据集分布规律的新样本［24］,其原理详见附录B。

考虑到上一章自适应整定算法处理的量测数据（终端周期性上送的电流、有功功率及开关闭合状态）均为时序数据,且实际配电网收集的训练数据集也容易存在缺失情况,故在WGAN 中采用能充分学习时序数据缺失规律的填充循环神经单元（gated recurrent units for imputation,GRUI）［25］,从 而 可 对缺失的量测数据进行有效学习并填充缺失值。

改进WGAN 的模型框架如图2 所示,生成器与判别器主要由GRUI 和全连接层神经网络组成,鉴于纯随机噪声不能有效地保存列间信息,将其与不完整训练数据共同作为生成器的输入,从而使生成器的输入得到很大程度优化。

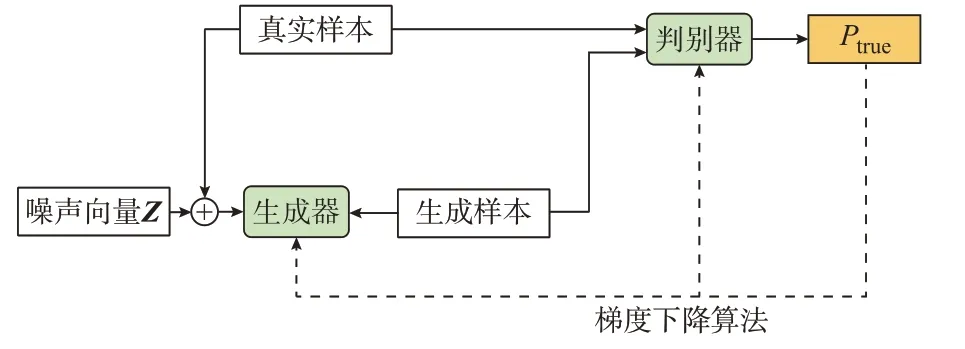
图2 改进WGAN 的整体框架Fig.2 Overall framework of improved WGAN

在生成器中,随机噪声和不完整数据经全连接层网络后输入GRUI 层,生成相应时间指标的隐藏状态,随后不断自我迭代,最终合成的时序序列即为生成数据。在判别器中,生成数据和不完整数据共同输入判别器,经GRUI 处理后,将最后一个隐藏状态反馈给全连接层,经sigmoid 函数后生成判别器判为真的概率值Ptrue。

相比于配电网正常运行时的量测数据,实际配电网发生故障的量测数据量少且较难获取,故本文仅使用配电网正常运行时的量测数据训练改进WGAN,本文所提的整定方法也通过配电网正常运行时的量测数据进行定值调整,而在故障期间终端不会向主站上送量测数据,此时终端处的电流保护继续使用上次调整的保护定值。

缺失量测数据重建后,针对可能存在的异常数据,为减轻计算负担,下面将提出一种原理简单的物理驱动方法对此进行辨识与修正。

2.2 异常量测数据的辨识与修正

为反映馈线回路（指系统电源至负荷或IIDG 所流通的路径）中开关的上下级关系,定义馈线回路开关矩阵,其行代表回路,列代表开关。当某一回路某开关运行状态为0 时,则本回路该开关的所有下级开关运行状态均为0,综合矩阵内各开关对应的各列数值,最终可得所有开关的运行状态序列。

根据配电网量测数据的两个特征规则对量测数据（电流或功率）信任度［26］进行评价,评价前需要以下近似处理:单开关线路首末两端的有功功率相等；通过采用“双点遥信”、开关状态与事件顺序记录核对确认等手段,加上开关状态的缺失重构精度高,认为开关运行状态序列是可以可靠获得的。具体评价规则如下。

1）开关“二遥”规则:若序列值为0 的开关对应量测数据也为0,则该量测数据的信任度加1。

2）母线、“线路”模型规则:考虑实际工程中互感器精度和采样非同时性的影响,当母线关联量测数据与线路上两直接相连测点数据分别满足式（11）、式（12）时,对应数据的信任度均加1。

所有量测数据完成评价后,根据所得的信任度进行如下异常量测数据修正:

步骤1:遍历所有“线路”模型,当两直接相连测点数据或其信任度不同时,较低信任度的测点数据或其信任度用较高信任度的对应值替代。

步骤2:遍历所有母线模型,当母线模型相关测点数据不满足母线模型时,信任度最低的测点数据通过其余值求解,且其信任度替换为其余信任度中的最低值。

步骤3:重新进行信任度评价,并比较本次与上次的信任度总数,若不再变化,则结束循环；否则返回步骤1 继续修正。

对于修正后信任度仍为零的量测数据,可将其剔除,并返回缺失数据重构模型进行数据重构,直至其信任度不再为零或达到循环限定次数后退出循环。

综上,本文所提计及量测数据缺失及错误的配电网电流保护自适应整定算法流程如图3 所示。其中kmax为设定的最大迭代次数。

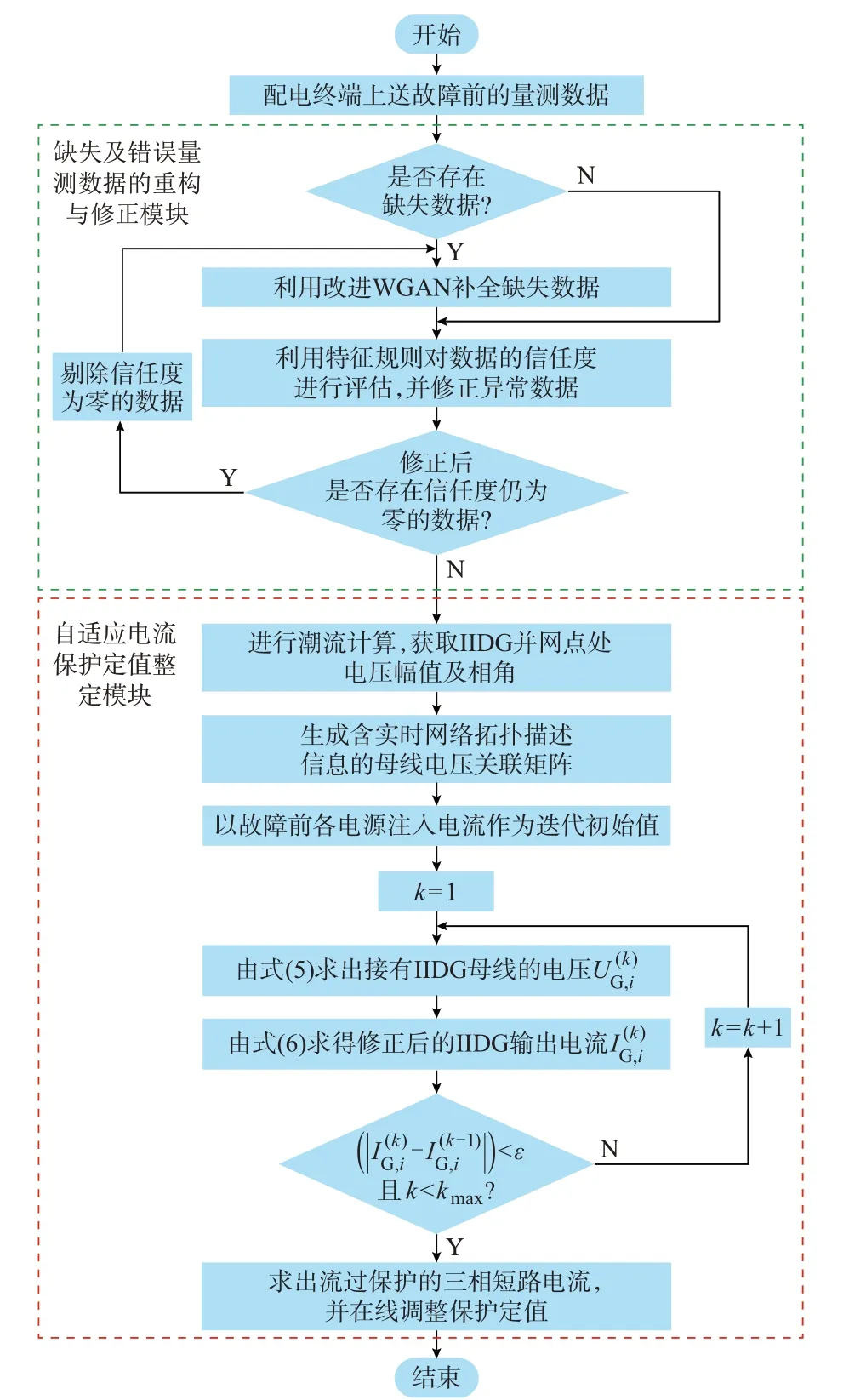
图3 电流保护自适应整定算法流程图Fig.3 Flow chart of adaptive setting algorithm for over current protection

3 算例验证

3.1 缺失及错误量测数据的重构与修正

在PSCAD/EMTDC 中搭建如图1 所示配电系统仿真模型,系统电源额定电压为12.66 kV,内阻为（0.5+j1.2）Ω,IIDG 额定容量为3 MW,线路单位长度阻抗为（0.27+j0. 245）Ω/km,母线间线路长度均为8 km。通过IIDG 及线路投退、IIDG 出力变化模拟配电系统运行方式变化,采集所有开关的运行状态、流经电流、有功功率,构建训练、测试数据集,共计获得数据组数为（13 950,20,3）,按9∶1 分配训练集与测试集。由于本文WGAN 的生成器和判别器所采用的是GRUI 网络,在实际系统收集训练样本时,含缺失的时序量测数据也可作为训练数据；且考虑到配电网量测数据规模较小,可尽可能多地收集配电网不同运行方式下的量测数据集,使得训练样本具备一定的典型性,训练的生成器也将生成更加符合真实数据的重构数据。

由于计划检修等原因,图1 中开关4 断开,以正常运行时某时刻电流量测数值为例,假设配电终端受外界环境或通信影响,测点编号为2、4、7、9、11 的量测数据全部丢失,测点编号为10、13、15 的量测数据出现错误,其余测点均正常,以上3 种量测数据分别用蓝、红、绿3 种颜色显示,各终端上送至主站的某相电流如图4 所示。

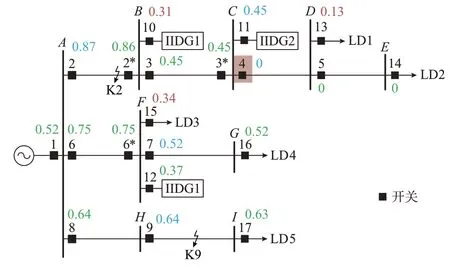
图4 各终端上送至主站的电流信息Fig.4 Current information sent from each terminal to master station

首先利用训练好的改进WGAN 模型对缺失的量测数据进行重构,重构效果如附录C 图C1 所示,可见在缺失率不高的情况下,开关运行状态、电流、有功功率三者的重构值均非常接近真实值,即此时模型已经充分学习到量测数据的时空分布特性,可以较为精确地重构出缺失值。

建立一个与量测数据维度一致的二值掩码矩阵模拟数据缺失,分析在不同缺失率下开关运行状态的重构误差,其重构误差为零的占比如附录C 表C1所示,在缺失率小于40%的情况下,开关运行状态的重构误差很小,一般情况下可以忽略。

引入均方根误差（RMSE）评价指标XRMSE衡量改进模型的重构效果。

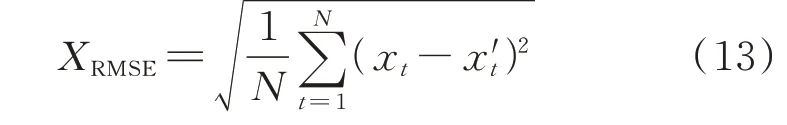
式中:xt为缺失数据的真实值；x't为缺失数据的重构值。

不同缺失率下2 种重构方法的RMSE 如表1 所示。表中10%、20%、30%、40%表示对应的量测数据缺失率。由表1 可见,对不同的量测变量,改进的WGAN-GRUI 重构效果要优于WGAN-GRUI,改进后重构方法的RMSE 最大可降低至改进前重构误差的42.8%。

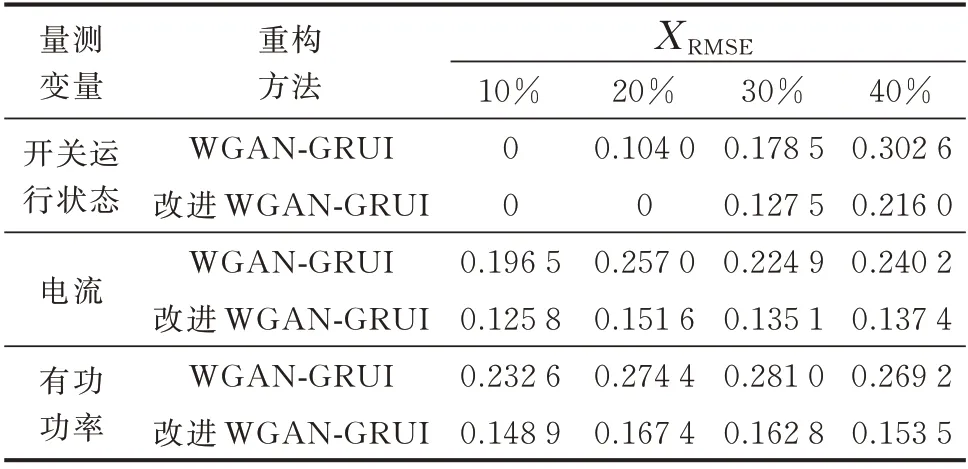
表1 不同随机缺失率下两种重构方法的误差对比Table 1 Error comparison of two reconstruction methods under different random missing rates

得到完整的量测数据后,基于母线、“线路”模型及开关“二遥”规则对重构后所有终端量测数据进行信任度评价,评价结果如附录C 表C2 所示,此时信任度共计22。

遍历所有“线路”、母线模型进行异常数据修正,修正后10、13 测点的异常数据被改正,再次对各测点量测数据信任度进行评价,评价结果如附录C 表C3 所示,此时信任度共计31,比上次评价时大,继续进行数据和信任度修正,但信任度总和不再变化,结束循环。

对于此时信任度仍为0 的12、15 测点可将其数据剔除,并返回缺失数据重构模型进行重构,生成完整数据后再进行不良数据修正,最终主站可获得完整且正确的量测数据。

3.2 自适应电流保护性能分析

量测数据处理后,主站系统将实时迭代计算各电流保护定值,本次求解通过MATLAB 程序计算,取最大迭代次数为20 次,迭代修正的容许误差为0.001。

以图4 中的保护4 整定为例,测试本文所提算法的计算速度。经测试可得,该算例的缺失及异常量测数据处理环节用时16.47 ms,故障电流迭代计算次数为4次,整定用时251.40 μs,共计用时16.72 ms。考虑到本文自适应整定方法所需的量测信息均为故障前信息,对电流保护定值整定的计算速度要求不高,利用一般微机保护的数据处理能力即可满足。

为测试所提自适应电流保护的动作性能,以图4 中的保护2 和保护4 为例,在线路2 末端设置两相短路和不设置故障分别进行测试,测试结果如表2所示。对比传统定值保护与本文所提保护的灵敏度可知,本文所提自适应电流保护可以提高IIDG 接入点上游保护的灵敏度。对比两种方法动作情况可知,本文所提自适应电流保护可以提高IIDG 接入点下游保护的动作可靠性。

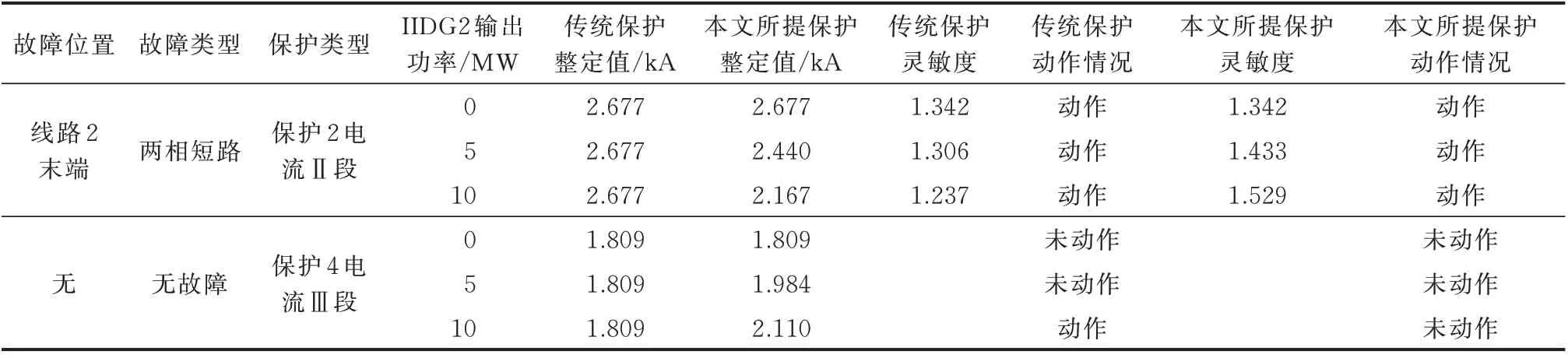
表2 不同IIDG 出力时保护动作结果Table 2 Protection operation results with different IIDG outputs

与传统电流保护一样,本文所提自适应电流保护的动作性能会受到过渡电阻的影响,但可以满足配电网对保护耐过渡电阻能力的要求。在实际配电网中,经常将阶段式电流保护与零序电流保护配合使用,零序电流保护可在经较大过渡电阻接地故障时保持较高的灵敏度,可靠切除故障。

设置在线路9 中点处发生三相短路,对比不同拓扑结构下传统定值保护与本文所提保护的动作性能,对比结果如表3 所示。在故障发生前,本文所提自适应电流保护会根据拓扑变化情况自适应更改保护定值,可以适应网络拓扑的动态变化；不同运行情况下发生故障,保护均正常动作,而传统定值保护存在拒动风险。

表3 不同拓扑结构时保护动作结果Table 3 Protection operation results with different topologies

4 结语

本文提出一种计及量测数据缺失及错误的电流保护自适应整定算法,解决了配电网运行方式变化和量测数据质量导致的电流保护动作性能下降问题,有以下结论:

1）实时量测信息经相关关联矩阵引入电流保护自适应整定算法后,所提保护可以适应配电网运行方式的动态变化；

2）根据终端上送量测数据的时序特性和拓扑形态特征规则,本文提出基于改进WGAN 的缺失数据重构算法和基于信任度的异常数据修正算法,可以较好地解决基于局域通信保护存在的量测数据质量问题。

算例测试结果表明,所提自适应整定算法可精确重构缺失数据及修正错误数据,并能较好地解决IIDG 接入及配电网运行方式变化给传统电流保护带来的难题。然而受线路老化等各方面影响,实际运行的配电网线路阻抗变化较大。因此,如何在线路阻抗不明确的情况下,利用多点量测信息进行电流保护定值的自适应整定,将是下一步的研究重点。

附录见本刊网络版（http：//www.aeps-info.com/aeps/ch/index.aspx），扫英文摘要后二维码可以阅读网络全文。