基于自适应黑盒反演的行波精确检测方法

雷 柳，李泽文，夏翊翔，黎文娇，穆利智

（1. 长沙理工大学电网安全监控技术教育部工程研究中心,湖南省长沙市 410114；2. 国网重庆市电力公司永川供电分公司,重庆市 402160；3. 中电智慧综合能源有限公司,北京市 102100）

0 引言

电网故障产生的行波信号中,其高频部分含有丰富的故障信息,具有工频故障信息所不能比拟的优点。行波技术是典型的基于暂态分量分析而产生的定位技术之一。暂态信号的提取是行波技术实用化的关键,而获取准确的暂态信号的前提是精确检测行波信号。因此,准确获取电网故障行波对提高行波技术的实用性具有重大意义［1-4］。

由于现有测量技术水平的限制,无法直接获取电网侧故障一次行波信号,只能通过互感器等装置测量得到传变之后的二次信号进行行波定位,如文献［5］验证了容性电压互感器检测到的二次信号可进行行波定位,表明容性电压互感器的二次信号能够反映电网故障一次行波信号的暂态特性,为行波技术的实际应用提供了理论基础。中国现有自主研制并投入现场使用的输电线路故障电流行波检测装置均利用电流互感器二次侧的行波波头信息进行故障定位［6-7］,然而互感器因自身物理特性不足、信号采集模块对各特征频段行波信号的传变特性不同等原因,使得电网一次行波信号经互感器、检测模块等传变后波形会发生一定程度的变化,出现二次检测波形与一次波形特征不一致的情况,严重时会导致电力系统安全监控、保护控制等出现误判,影响系统的安全稳定运行。

目前针对信号经行波传感器传变后出现波形畸变的问题,主要有2 种解决思路:1）研究传感器内部结构,减小畸变程度,如文献［8-9］研究了基于Rogowski 线圈测量的波形畸变校正方法；2）利用二次侧行波信号反向推导一次侧信号,获取真实的一次侧信号。目前获取实际故障暂态信号大多使用第2 种方法,这种反向推导的过程就是典型的反演问题求解过程。

针对信号反演问题,文献［10］在对行波传感器准确建模的前提下,基于行波传感器模型的传递函数建立传感器反模型,利用Tikhonov 正则化方法解决反演问题求解过程中出现的病态问题,但正则化参数对反演结果影响较大。文献［11］利用经验模态分解和维纳滤波对行波信号进行反演,但分解过程中存在模态混叠效应,影响反演精度。上述方法都是在基于行波传感器模型的正演传递函数基础上求解反函数,需要对传感器进行精确的建模,一旦传感器模型参数设置有偏差,就会影响反演算法的求解和反演精度。文献［12］提出最小均方滤波器应用于热工过程对象建模,建立的模型与未知系统的差分方程和传递函数等价,具有辨识精度高、计算简单和自适应能力强等特点。文献［13-14］针对电流互感器饱和后二次信号的畸变问题,利用神经网络算法对畸变波形进行修正,但互感器型号的选择对补偿效果影响较大,且对二次信号的补偿不能很好地复现一次信号。上述理论研究为本文所提问题提供了解决思路和理论依据。因此,为解决行波信号经传感器传变后的衰减与畸变问题,同时避免传感器传变函数不精确对反演精度的影响,提出了一种无须基于传感器传递函数的反演方法。仿真和实验结果表明,通过本文方法获得的反演一次行波与实际一次行波信号非常相似,有较好的可行性。

1 一、二次行波差异分析

当电网发生故障时,电容式电压互感器的地线电流会发生突变,利用这一特点研究专用电压行波传感器,基于Rogowski 线圈原理测量获得电压行波代表突变的地线电流。该传感器的测量原理如图1所示。

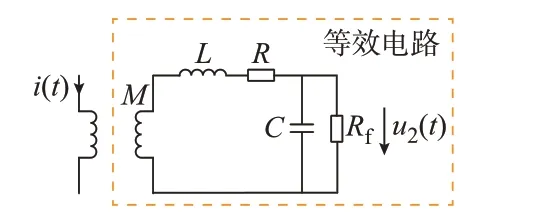
图1 行波传感器的等效电路Fig.1 Equivalent circuit of traveling wave sensor

图1 中:i(t)为流经互感器接地线的电流信号,即一次行波信号；M为互感；L为线圈自感；R为内阻；C为分布电容；Rf为采样电阻；u2(t)为传感器采集到的行波信号,即二次行波信号。当电力线路上发生故障时,一次行波信号i(t)会发生突变,此时利用电压行波传感器采集得到的信号为二次行波信号u2(t)。在实际线路中,u2(t)可通过传感器测得,而线路上的真实故障信号i(t)无法直接获得。

通过行波传感器的电路模型进行仿真,其中一组仿真结果见附录A 图A1。图A1 的仿真结果显示,一次行波信号经传感器传变后会出现波形畸变,也就是二次行波不能完全代替一次行波。为验证这一结论,在较为理想的环境下进行了实验验证。利用行波发生器、电压行波传感器和数字示波器等设备获取不同故障类型、不同检测点的实测一、二次行波信号,其中一组结果见附录A 图A2。由图A2 可知,一次行波经行波传感器传变后得到的二次行波与一次行波的波形特征明显不同,且一、二次行波之间的差异是由测量装置行波传感器引起的。只需建立传感器由二次到一次行波的反模型,就可以实现电压行波信号的精确检测。

2 黑盒模型

由一次行波信号得到二次行波的系统称为行波传感器,由二次行波得到一次行波的系统称为黑盒,即上文提到的传感器反模型。由二次行波信号得到一次行波信号的过程称为反演。经上述分析可知,一、二次行波之间的差异由传感器引起,所以可通过训练学习大量的一、二次行波信号研究一、二次行波之间的传变关系,即黑盒模型。在实际线路中,检测到的二次信号都会因各种原因含有大量噪声,导致在分析信号时产生不必要的干扰,所以为保证反演精度,需先对二次信号进行预处理（去噪）,再利用自适应滤波器学习得到黑盒模型的参数矩阵H,完成黑盒模型的构建。反演流程如图2 所示。图中:y'为信号预处理后的二次信号；Wopt,m为m时刻的最佳权重。

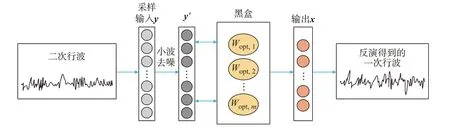
图2 反演流程Fig.2 Inversion process

设一次信号为x,二次信号为y,基于离散反卷积原理的一、二次信号之间的关系可表示为:

因为传感器模型的参数矩阵A条件数很大,所以式（1）是一个病态方程组,即参数矩阵H不是参数矩阵A的逆矩阵,不能通过求逆解出。因此,本文提出通过自适应算法训练一、二次信号获得两者之间的传变关系,即参数矩阵H。

2.1 自适应滤波器原理简介

自适应滤波器的研究始于20 世纪50 年代末,其在未知环境下能够很好运行并跟踪输入量随时间的变化。自适应信号处理已经成为信号处理学科的一个重要分支,并广泛应用于工业控制、通信、生物医学和地震学工程等方面［15］。自适应滤波器的原理图见附录B 图B1,预处理过的二次信号作为自适应滤波器的输入,通过自适应算法训练获得黑盒模型的参数矩阵H。

自适应算法的目的是通过将误差信号e(n)反馈至滤波器来调整滤波器的权重W（n）,使预测的一次信号x（n）与真实的一次信号g不断接近,获得最佳权重系数Wopt(n),再利用最佳权重系数对真实的一次信号与预处理后的二次信号之间的关系进行建模,得到黑盒模型的参数矩阵H。自适应滤波器内部的算法有很多,其中最小均方误差（least mean square,LMS）自适应算法因具有易于实现、算法简单和鲁棒性高等特点而得到广泛的应用。

2.2 信号预处理

信号预处理的目的是去除噪声并保持局部特性,小波阈值去噪是小波去噪方法中应用最广泛的一种,所以本文采用最常见的小波阈值去噪方法。小波阈值去噪流程见附录B 图B2［16］。首先,对含噪声的原始信号在各尺度上进行小波分解,得到不同幅度值的小波系数；通常噪声信号的小波系数相对较小,可设定一个阈值,保留有价值的主信号；最后,通过逆小波变换重构信号,提取出有效的信号。其中阈值函数和阈值的选择是最关键的2 步。

2.2.1 阈值函数的选择

阈值去噪中最常用的函数有软阈值函数和硬阈值函数,其中软阈值函数的整体连续性较好,采用软阈值函数获得的重构信号具有更好的光滑性,但原始信号中包含的小奇异点易被作为噪声滤除,造成信号失真,影响重构信号的真实度。而采用硬阈值函数去噪后的信号边缘特性与原始信号基本保持一致,所以本文选用硬阈值函数。

硬阈值函数可表示为:

式中:N1为分解后小波系数的个数总和；σ 为附加噪声信号的标准差。

3 变步长LMS 算法

3.1 LMS 算法

LMS 算 法 于1960 年 由Widrow 和Hoff 提 出,是一种对目标函数进行适当调整的搜索算法,具有性能稳定、简单、计算量少、利于实时实现的优点,可对梯度向量的计算进行简化,是目前最为常用的自适应滤波算法［12］,通常包含滤波过程和自适应过程。滤波过程通过一个横向滤波器完成,输出包括线性滤波器对输入信号的输出响应以及输出响应与期望响应之间的估计误差。自适应过程中,LMS 自适应滤波器依据最速下降算法的原理计算抽头权重向量,使延时信号的加权和逼近输入的期望信号d,并自动调整相应参数,以达到最优滤波的效果。

以长度为m+N的输入信号Ym+N为例,使m时刻的输出信号Xm逐渐逼近期望信号dm,其过程如附录C 图C1 所示。图中:Xm(n)为m时刻滤波器的总输出信号；em(n)为m时刻滤波器第n次迭代输出的误差向量。

LMS 自适应滤波器输入一个完整信号Ym+N和一个期望信号dm。第i时刻的输入信号的感受野区间Yi与其对应的第n次迭代的权重向量Wi(n)以式（5）加权得到第i时刻的估计输出信号xi(n):

式中:μ为LMS 算法的步长因子,具体取值见3.2 节。

利用式（7）进行权重向量组的迭代更新,每次迭代输出一个估计信号Xm(n)和误差信号em(n),直至误差不再减小,即输出的估计信号Xm和期望信号dm最接近时,得到输入信号与期望信号之间的最佳权重向量Wopt。

3.2 改进步长LMS 算法在行波反演中的应用

传统定步长LMS 算法存在以下矛盾:当选取较大步长时,收敛速度快,但稳态误差较大；当选取较小步长时,稳态误差小,但需要较长的时间收敛［17-18］,即不能同时保证收敛速度快和稳态误差小。文献［19］提出一种改进步长LMS 算法,该算法使用时变步长代替定步长算法。本文采用该改进步长LMS 算法用于行波反演。

改进步长LMS 算法通过在步长与误差信号之间建立某种函数关系来缓解上述矛盾:当误差较大时,选择较大步长加快收敛速度；当算法趋于稳态时,选择较小步长使算法稳态误差较小。改进后的步长因子为:

式中:μ(n1)为第n1次迭代时的步长因子；α(n1)为控制步长函数变化快慢程度的变参数函数；β(n1)为控制算法收敛速度的变参数函数；e(n1)为第n1次迭代时的误差；η、p、m1、q为常值参数。

为保证黑盒模型的精确度,在LMS 自适应反演算法中会考虑使用大量样本进行训练,以不同故障类型、不同行波检测点处的行波一、二次信号作为样本输入,h个样本通过LMS 自适应滤波器训练学习的模型如图3 所示。

图3 含多个样本的LMS 自适应训练模型Fig.3 LMS adaptive training model with multiple samples

每一组样本包括需要反演的二次信号Yh和作为期望信号的真实一次信号d,且每组样本都对应一个LMS 自适应滤波器,各自适应滤波器采用同一个权重向量W,其初始值W(0)取零。通过LMS 自适应滤波器训练后输出(X,e),包含每组样本的估计输出信号Xh和误差信号eh,然后,求取各样本误差e的平均值以及各样本误差e与二次信号Y乘积的平均值,再通过权重向量更新式（11）反馈至滤波器更新权重向量组,直至样本的误差的平均值不再减小,存储此时的最佳权重向量组。

4 仿真分析

4.1 故障信号的获取

在仿真软件PSCAD 中搭建IEEE 9 节点标准测试系统模型,系统结构见附录D 图D1,其具体模型为:电压等级为220 kV,线型为二分裂,分裂线间距为400 mm,线径为26.82 mm,导线和杆塔对地高度分别为10 m 和21 m,导线间距为3.5 m,弧垂为6 m。

设置采样频率为1 MHz,利用PSCAD 软件获取系统的一次故障波形,再通过MATLAB/Simulink 搭建传感器模型,获取仿真二次侧行波。为保证黑盒模型的精确度,样本的获取要考虑不同故障位置、故障初相角、过渡电阻和故障类型4 种情形。

1）不同故障位置

系统中每条线路总长为100 km,故障线路在靠近母线4、7、9 一端设有行波故障检测点,其中故障距离是指距离行波检测装置的距离。系统中发生故障的位置有30 种基本情况,如表1 所示。为减小训练量的同时保证训练的准确度,仿真中选取序号为1、3、5、7、8、10、12、13、14、16、19、20、21、22、24、25、26、28、29、30 的20 种情况。

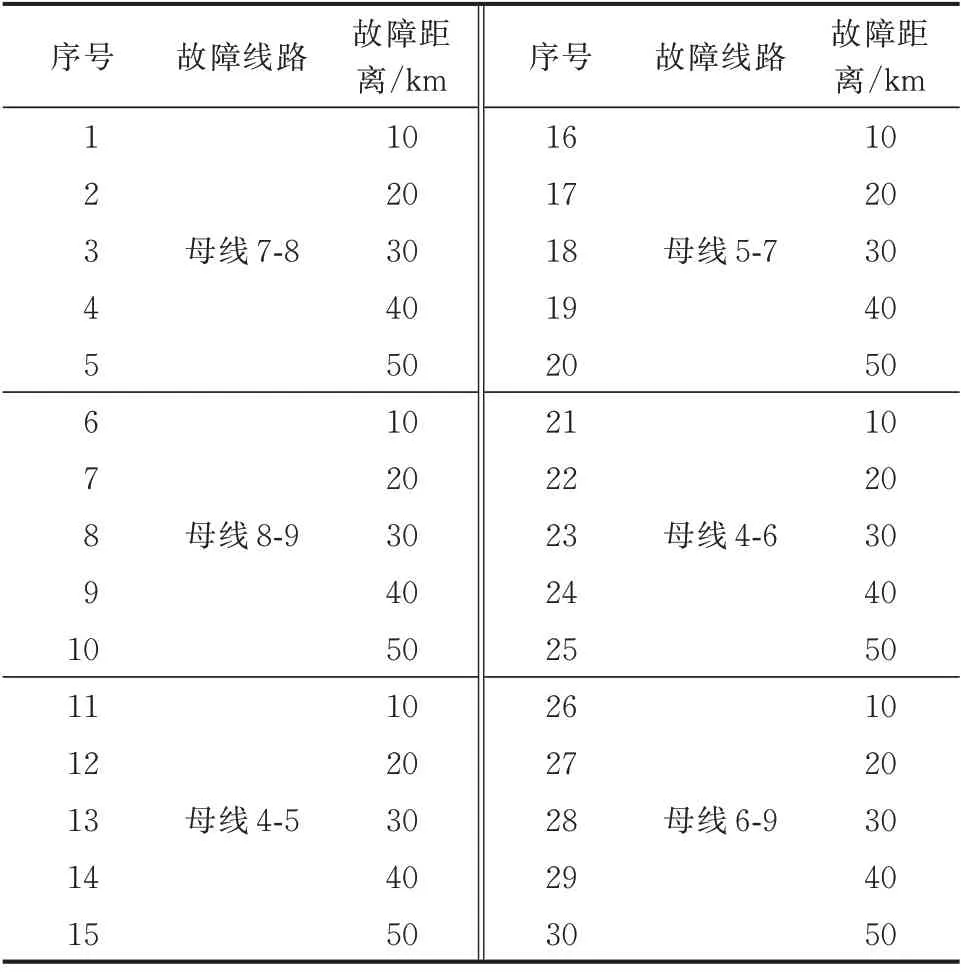
表1 不同故障距离的情况Table 1 Condition with different fault distances

2）不同故障初相角和过渡电阻

故障行波幅值取决于故障点的附加电势,当故障电压初相角特别小时,行波突变幅值也较小,经过线路传播过程中的衰减,行波波头难以检测。由实际运行结果表明,故障初相角大多在峰值30°范围内,故障角小于15°的情况极少,因此,故障角设置为9 种情况（10°,20°,…,90°）。过渡电阻在1～300 Ω 范围内取1、10、50、300 Ω,为此不同故障初相角和不同过渡电阻情形有36 种基本情况,如表2 所示。为减小训练量的同时保证训练的准确度,仿真中选取序号为1、3、5、7、9、11、12、14、15、17、19、21、23、24、27、28、30、31、34、36 的20 种情况。

表2 不同故障初相角、过渡电阻的情况Table 2 Condition with different fault initial phase angles and transition resistances

3）不同故障类型

为保证训练的准确度,还需考虑不同故障类型下的故障信号,本文考虑了单相接地故障和两相接地故障2 种情况。因此,本文获取的数据有20×20×6=2 400 组,随机取其中90%（2 160 组）数据用作训练样本,剩下10%（240 组）数据用作反演验证。

4.2 反演结果

设滤波器的抽头数N=100,样本中一次信号和二次信号的采样数为1 000；初始权重矩阵设为100×901 的零矩阵,每个时刻滤波器的感受野区间对应的权重向量就是权重矩阵的列向量。通过上述2 160 组样本训练得到最佳权重矩阵Wopt,也就是仿真模型中传感器的黑盒模型参数矩阵H；再利用上述240 组二次行波信号经过黑盒模型输出得到反演的一次信号,以此验证本文方法的可行性。

以2 组波形反演结果为例,第1 组波形反演的结果见附录D 图D2,该组波形故障情况是母线4 与5 间发生AB 两相接地短路故障,故障距离为30 km,过渡电阻为50 Ω,初相角为30°。由图D2 中仿真二次波形可看出,第1 组波形经传感器传变后畸变程度很大,幅值相差高达十几倍,也更加证明了研究反演获得一次行波信号的必要性；由图D2 中反演得到的一次波形和仿真的一次波形可看出,两者的误差很小,可以根据式（13）计算反演一次行波信号与仿真一次行波信号的波形相关系数。

式中:ρ(x',x″)为仿真一次信号x'与反演一次信号x″的相关性系数；x'i和x″i分别为第i时刻的仿真一次信号和反演一次信号；T为信号总长度。ρ(x',x″)的值在-1 到1 之间,正负号表示相关方向。ρ(x',x″)的绝对值越接近于1 表示2 个信号波形越相似且相关性越大。经计算,二次行波信号经本文黑盒模型反演得到的一次波形与仿真一次波形之间的波形相似度为0.996。

第2 组波形反演的结果见附录D 图D3,该组波形故障情形是母线6 与9 间发生B 相接地短路故障,故障距离为40 km,过渡电阻为10 Ω,初相角为80°。同理,对于图D3 中仿真二次波形,以及反演得到的一次波形和仿真的一次波形,经计算,二次行波信号通过本文黑盒模型反演得到的一次波形与仿真一次波形之间的波形相似度为0.995,从而证明黑盒模型的反演精确度很高,能实现一次行波信号的精确检测。

4.3 变步长和定步长算法的对比

为体现变步长算法与定步长算法性能的不同,针对不同步长,将仿真一次信号与反演一次信号之间的误差之和分别通过仿真得到相应的收敛曲线,如附录D 图D4 所示。当步长较大时,取μ=0.8,收敛的速度较快,很快就能达到稳态,但达到稳态时误差较大,收敛性不好；当步长较小时,取μ=0.2,稳态时误差较小,但收敛速度慢,收敛时间较长。

为解决稳态误差和收敛速度无法同时满足的矛盾,本文采用了改进步长算法进行反演,通过多次仿真发现,当q=0.2,p=0.97,η=95,m=0.5 时,改进步长算法的性能最佳,其收敛曲线见附录D 图D4。当误差较大时,采用大步长,收敛速度较快；当误差较小时,采用小步长,稳态性能较高,稳态误差较小。由此可以看出,改进步长LMS 算法进行反演的收敛性和稳态性能更好。

4.4 抗噪能力

在实际线路中,检测到的二次信号都会因各种原因含有大量的噪声,因此,为检测本文反演算法的抗噪能力,设置母线7 与8 之间发生A 相接地故障,故障距离为40 km,对二次信号加入信噪比为40、30、20、10、6 dB 的白噪声,在不同故障条件下进行反演,其结果见附录D 表D1。

由附录D 表D1 可知,在不同信噪比、不同故障角的情况下,通过本文所述方法反演得到的一次行波信号与仿真一次信号相似度较高,能够反映电网故障时真实的故障信息,具有较好的鲁棒性。

4.5 反演算法的对比

为验证本文反演算法的优越性,将本文所提算法与文献［10］提出的Tikhonov 正则化反演方法进行比较。其中,Tikhonov 正则化方法是以传感器的传变函数为基础,结合离散反卷积和Tikhonov 正则化完成电压行波的反演；本文方法通过训练获得一、二次信号之间的传变关系,建立反演模型,再进行反演。在附录D 图D1 的仿真系统中,在母线8 与9 之间设置C 相短路接地故障,故障距离为20 km,过渡电阻为300 Ω,初相角为50°。2 种方法的反演结果对比见附录D 图D5。由图D5 可知,Tikhonov 正则化方法的反演精度不如本文所述方法。这是因为Tikhonov 正则化反演方法需先对传感器进行精确建模,再建立反演模型,一旦传感器模型参数设置有偏差,就会影响到反演算法的求解和最终反演结果的精度,而本文方法无须借助传感器传递函数求解反演模型,可避免传递函数不精确对反演结果的影响,反演精度更高,适用性更强。

5 实验验证

本文在实验室应用相关设备进行行波测试,实验室测试图如图4 所示。利用所研制的电网故障行波发生器（XBFSQ-6K/3000）模拟输电线发生故障时产生的暂态信号,即一次行波信号。故障行波发生器可以模拟各种故障类型和不同故障程度的故障,开路输出电压最大值为（6±5%）kV,波前时间为（1.2±30%）μs,脉冲半波峰时间为（50±20%）μs。在电网故障行波发生器输出线路上,串接电容器为电容式电压互感器等效电容,并套接行波传感器进行行波检测。通过数字示波器测取电网故障行波发生器输出线路上的串接无感电阻（小阻值）端电压和行波传感器输出端口电压,得到多组实测一、二次行波波形。通过黑盒模型根据实测二次行波反演获取一次信号,再对反演一次行波与实测一次行波进行波形对比,验证本文方法的有效性。

图4 实验室测试图Fig.4 Lab test diagram

为验证本文方法的有效性,选取其中一组实测一、二次行波波形如附录E 图E1 所示。将该组二次行波信号输入黑盒模型得到反演一次行波信号,其结果见附录E 图E2。经计算,反演得到的一次行波信号与实验一次行波信号相似度较高。实验结果表明,本文方法对实验中的行波信号也能实现精确反演,无须依赖传感器的传递函数,避免了传递函数不精确对反演结果产生的影响,有效提高了行波检测的真实性。

6 结语

本文提出一种基于改进步长LMS 自适应反演算法的行波波形精确检测方法,通过训练传感器的一、二次信号找到两者之间的传变关系,建立黑盒反演模型进行反演。具体结论如下:

1）该方法无须借助传感器传递函数求解反演模型,可避免传递函数不精确对反演结果的影响,有效提高行波检测的真实性,推进行波技术的实用化；

2）利用改进步长的思想解决训练中收敛速度与稳态误差之间的矛盾,使其在误差较大时拥有大步长,收敛速度快；当误差较小时拥有小步长,稳态误差小,并通过多次仿真得到,当q=0.2,p=0.97,η=95,m=0.5 时,改进步长算法的性能最佳；

3）利用小波阈值去噪法对二次信号进行预处理,通过仿真表明本文方法抗噪能力强,即使二次信号含有噪声,其反演精度也很高；

4）通过不同故障线路、初相角、故障类型及过渡电阻情况下的大量仿真和实验测试表明,本文反演方法的精度高,适用性强。

在预处理过程中采用最常用的小波去噪方法且只考虑最常见的白噪声,与实际情况会有出入,所以后续会针对预处理部分展开研究。

附录见本刊网络版（http：//www.aeps-info.com/aeps/ch/index.aspx），扫英文摘要后二维码可以阅读网络全文。