考虑光伏出力相关性的主动配电网薄弱环节识别
孙媛媛,程凯强2,,许庆燊,李道宇,李亚辉
(1. 山东大学电气工程学院,山东省济南市 250061;2. 国网扬州供电公司,江苏省扬州市 225009)
0 引言
伴随“双碳”目标的大力推进以及乡村振兴战略的贯彻落实,大量分布式光伏接入中低压配电网,配电网呈现分布式光伏出力相关性显著、电压越限风险高和网架结构脆弱等特征[1-3],配电网出现了受光伏出力相关性影响的高越限风险以及网架结构薄弱环节,对供电可靠性和电能质量造成影响[4-5]。主动配电网的薄弱环节识别作为将配电网可靠性评估和网架结构优化联系起来的纽带,提高识别精确性对提升配电网供电能力具有重要意义。
电力系统薄弱环节通常指因扰动或故障后对电力系统安全性影响较大的设备元件[6],风险性评估是薄弱环节识别必须考虑的方面之一。现有识别方法主要从状态薄弱性和结构薄弱性两方面展开。状态薄弱性侧重于电网长期运行面临的越限风险,基于风险理论和潮流建立指标[7-8];结构薄弱性侧重于网架结构的拓扑脆弱程度,基于复杂网络算法建立指标[9-11]。
目前,针对配电网薄弱环节的研究较少,基本是基于配电网运行层级的风险评估,基于统计数据对过载线路进行识别。文献[12]基于配电网可靠性指标识别区域内的薄弱环节。文献[13]针对重庆配电网重过载、线路分段不足、电缆化率低、缺少联络开关、同杆架设严重等问题定义了薄弱环节判别依据,进而通过统计数据进行识别。文献[14]基于统计数据从供电能力、网架结构、电力设备等方面,分析了聊城市供电可靠性问题。综上,当前薄弱性评估既没有考虑分布式光伏出力相关性,也未深入到影响配电网安全可靠运行的元件层面。此类方法在实际工程中的应用以人的主观经验为主,没有进一步分析薄弱环节对供电能力的影响。因此,考虑光伏出力相关性,将状态薄弱性和结构薄弱性的评估细化至具体节点线路,准确提取薄弱特征,掌握配电网运行过程中各元件的越限风险及坚强程度,才能有效提高薄弱环节识别的工程指导意义。
针对上述问题,本文研究了考虑分布式光伏出力相关性的元件状态薄弱和结构薄弱特征指标,提出了配电网薄弱环节的识别方法。基于Copula 理论分析光伏出力相关性,基于联合分布拒绝采样法建立了光伏出力相关场景;研究基于重复潮流的薄弱程度量化方法,结合风险理论和效用理论提出了元件状态薄弱评估指标;考虑光伏出力相关性改进了结构薄弱评估指标,提出了线路供电薄弱度指标;基于最小二乘支持向量机(least squares support vector machine,LSSVM)综合状态薄弱性和结构薄弱性特征,搭建了配电网薄弱环节类型系统识别架构。
1 考虑光伏出力相关性的概率潮流
1.1 基于Copula 理论的光伏出力相关性分析
针对分布式光伏实测数据,采用基于Copula 理论的联合概率密度函数,通过秩相关系数分析光伏出力相关性,得到出力相关性的联合分布函数。Copula 函数将多个随机变量的联合分布用各个变量的边缘分布连接起来,能准确刻画各个变量间的非线性相关性。采用椭圆Copula 函数作为分析模型,该函数对于二元极值分布和非正态结构有较好描述效果,对作为研究关键的二维分布式光伏出力相关性具有极高的拟合程度及特点匹配特性。
F(x)和G(y)分别为二维分布式光伏实测数据的边缘分布函数,通过二维Gaussian Copula 分布函数C(F(x),G(y))的密度函数c(F(x),G(y)),可求出原联合分布函数的密度函数h(x,y)为[15]:
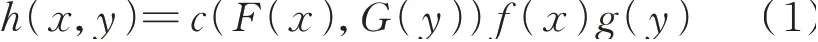
式中:f(x)和g(y)分别为F(x)和G(y)的密度函数,可通过核密度估计法得到。
1.2 基于联合分布拒绝采样的出力相关性场景建立
根据概率分布采样得到服从该分布的样本,通过聚类产生光伏出力相关性场景。为实现对高相关性的光伏出力复杂函数采样,采用拒绝采样法处理样本,采样样本能精准刻画与实际数据相同的分布特征。
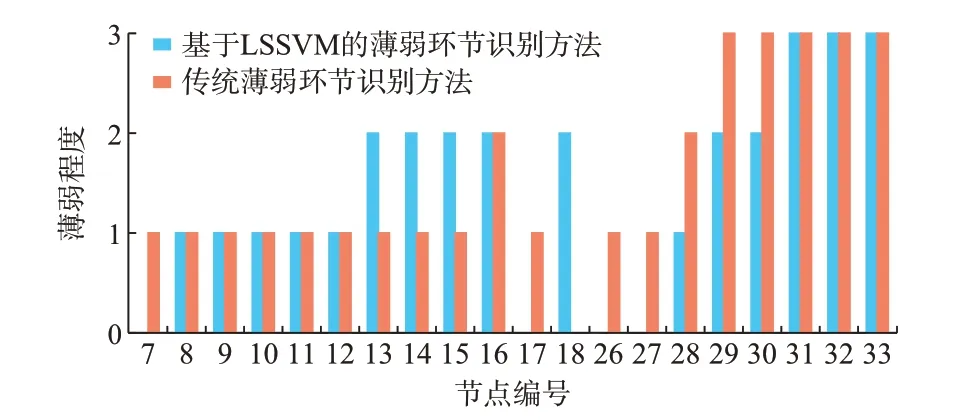
设置参考分布q(x,y)为二维正态分布概率密度函数。引入常数k,使得对所有的(x,y)满足kq(x,y)≥p͂(x,y),其中,p͂(x,y)为式(1)得到的光伏出力实测数据的概率密度函数。在每次采样中,首先从q(x,y)随机获取一个值(x0,y0),然后在区间[0,kq(x,y)] 均 匀 抽 样,得 到u0。 如 果u0 基于光伏相关性场景,结合半不变量与Cornish-Fisher 级数展开,提出基于蒙特卡洛法的概率潮流。蒙特卡洛法在已知负荷、分布式电源出力等k个输入变量累积概率密度函数的前提下,进行m次随机抽样,得到k×m组节点电压输出变量,再对输出变量进行概率统计分析[17]。然后,借助半不变量以及Cornish-Fisher 级数展开法得到输出变量的概率分布函数[18],如附录A 式(A1)和式(A2)所示。考虑节点电压、支路功率和变压器容量等约束,步骤如下: 步骤1:基于统计数据采用二维Gaussian Copula 函数得到分布式电源出力的联合概率密度函数,采用核密度估计法得到各个光伏出力的概率密度。 步骤2:采用拒绝采样法对分布式电源出力的联合概率密度和负荷功率的概率密度进行抽样,得到不同场景s的出现概率及服从对应分布的M组样本。 步骤3:基于每一组样本进行潮流计算,得到M组节点电压和线路电流。 步骤4:对于不同的节点电压值和线路电流值,计算节点电压统计值和支路电流统计值,包括均值、方差以及各阶矩。 步骤5:基于步骤4 所得结果计算输出变量的各阶半不变量,得出最终的各个概率分布函数值,再根据Cornish-Fisher 级数展开得到越限概率。 基于“伤害发生的可能性和该伤害带来后果的严重程度”[19]的风险定义,由越限概率与薄弱程度的乘积表示元件越限风险指标,提出了基于重复潮流和效用理论的薄弱程度量化方法。 重复潮流的本质是在约束条件下求取供电负荷的临界值[20]。按比例增长系统各个节点的负荷,通过在反复潮流计算中扩宽约束条件观察供电负荷的变化量,将各环节越限条件对于最大供电能力的影响作为薄弱程度的量化值,算法流程如附录A 图A1所示。 考虑到分布式电源出力相关性,引入了基于潮流计算的最大供电能力评估模型。将大规模分布式光伏易导致的并网点电压越限、变压器过载以及供电线路容量越限作为薄弱环节识别的主要方面。假设负荷按比例增长,最大供电能力评估模型为: 式中:λs为分布式电源出力相关性场景s出现的概率;Ss,DG为场景s下分布式电源的出力;n为场景数。由式(4)得到考虑相关性的各分布式电源出力初始值,与基于统计数据得到的负荷均值作为算法输入的初始值。 在计算得到各节点和线路供电薄弱程度的基础上,结合效用理论和越限概率可得到越限风险指标。选取冒险型效用函数u(x)[19]进行薄弱程度量化,表达式为: 3)节点电压越限风险 电压波动范围在(0.95,1.05)p.u.范围视为合格。同理,可以得到节点电压越限概率POut,V(越上限概率与越下限概率之和)和供电能力增长量LOut,V,其风险值ROut,V为: 在分布式光伏高相关性的配电网背景下,传统复杂网络特征量不再适用。对传统的度数、介数等指标[9]进行改进,运用复杂理论的特征指标建立结构薄弱性指标。 1)节点度数 在评估中引入与关注节点直接联系的所有节点产生的影响[22],定义节点度数DN,i为: 式中:Sb为节点容量基准值;Ps,i为相关性场景s下节点i的注入功率。该指标能够体现节点输送功率的能力,值越大说明该节点在配电网传输功率中越重要,薄弱程度越低。 4)线路供电薄弱度 基于线路的N-1+1 准则[19],结合考虑分布式电源的重复潮流计算,将线路N-1+1 后负荷增长倍数K作为线路供电薄弱度。由于配电网N-1+1 后可能会有多种闭合开关的选择,将其作为线路供电薄弱度的一部分,定义线路供电薄弱度HL,u为: 式中:Ku为在对线路u进行N-1+1 后所有闭合联络开关方案中负荷增长倍数的最大值;nRe,u为断开线路u后,闭合联络开关能恢复供电的失电负荷的个数。该指标值越小,表明该条线路遭遇故障后对配电网供电能力的影响越大。 5)节点介数 基于考虑分布式电源出力相关性的多场景对已有介数改进[22],定义节点介数BN,i为: 式中:Vs,i为在场景s下节点i的电压;Vb为节点电压基准值;Is,ij为在场景s下,在分布式电源接入的节点注入对应电流后,在支路ij上产生的电流;As为中间变量。 6)线路介数 针对分布式电源出力相关性场景提出线路介数BL,ij的表达式为: 式中:Ps,ij为在场景s下线路ij传输的有功功率;Pij,max为最大供电能力时线路ij传输的有功功率。改进后的线路介数指标可充分体现分布式电源出力相关性场景下的输送能力,其值越大说明线路越重要。 状态薄弱性评估和结构薄弱性评估是主动配电网综合薄弱环节识别的重要组成部分。已有研究采用层次分析法等主客观赋权的方法,通过简单排序将综合指标值较大的节点和线路视为薄弱环节[12],每项指标在综合后将一定程度上失去独立性。而采用LSSVM 识别薄弱环节类型,将提出的各项指标作为薄弱环节的特征值,在探索薄弱环节内在原因的同时提高了识别准确性。 基于LSSVM 的薄弱环节识别关键在于训练集的确定。 确定训练数据集 {xk,yk}lk=1(k=1,2,…,l),其中,xk为输入,采用所提出的考虑分布式电源出力相关性的状态薄弱性和结构薄弱性评估指标;yk为输出,为薄弱环节的类型。建立LSSVM模型f′(x)为: 式中:σ为RBF 核宽度。 考虑光伏出力相关性的主动配电网薄弱环节识别的整体流程如附录A 图A2 所示。所提出的方法完成从单个量化指标到综合辨识的提升,将配电网实际运维监测中排查出的薄弱环节作为训练集的输出,并根据越限时长等进行薄弱类型的划分。 基于某区域配电网2 个光伏电站的年出力数据,采用二维Gaussian Copula 函数分析其相关性,产生服从联合分布的样本,建立光伏出力相关性场景。2 个光伏电站出力的频率分布如附录A 图A3所示,可见不服从正态分布。对光伏出力数据归一化处理,2 个光伏电站的相关系数为0.988 4,2 个光伏电站出力的二维联合概率密度函数如附录A 图A4 所示,反映了二者出力具有极强相关性。拒绝采样分布采用均值为0.4、方差为0.2 的变量X和均值为0.4、方差为0.3 的变量Y,参数为-0.2 的二维正态分布,如图1 所示。产生了10 000 个服从建议分布的样本,基于拒绝采样法得到服从附录A图A4 所示概率密度函数的1 053 个样本。基于Kmeans 算法产生多个场景,通过聚类分析确定聚类数为6。具体场景如附录A 表A1 所示。场景2 至场景5 的相差不大,场景1 和场景2 的概率相对其他场景较小,这与所取光伏出力数据为日平均数据有关。 图1 二维概率密度函数拒绝采样图Fig.1 Rejection sampling graph of two-dimensional probability density function 采用IEEE 33 节点配电系统进行算例分析,配电变压器最大容量为10 MV·A,负荷为3.7 MW+2.3 Mvar。分别在节点16 和26 处接入光伏,最大出力均为1.5 MW。基于5.1 节得到的分布式电源出力相关性场景1 至场景6,加入8-21、12-22、9-15、18-33 和25-29 联络开关,修改后的配电网络拓扑如图2 所示。 图2 修改的IEEE 33 节点配电系统结构Fig.2 Structure of modified IEEE 33-bus distribution system 采用基于蒙特卡洛法的概率潮流得到各节点电压越限概率及线路电流越限概率。如附录A 表A2所示,越限概率较高的线路分布在光伏电站接入的支路中。线路1-2 的越限概率为1,一直处于越限状态,属于应立即处理的薄弱线路。线路2-3 和26-27的越限概率接近1,1 年中长时间接近越限状态,属于明显薄弱线路。对比节点和线路分析结果,支路电流均值会出现越限,各个支路电流的越限值存在较大差异,而节点电压均值均处在不越限区间内,各个节点电压越限值差异相对较小。 为分析光伏出力相关性对配电网薄弱性评估的影响,以考虑相关性前后的节点电压越限、线路电流越限为例进行对比。确保相关性作为唯一变量,用相同方法处理不同的光伏出力样本,场景1 未考虑光伏出力相关性,场景2 考虑了相关性。 以越限比较明显的节点15 电压为例,电压概率密度函数如附录A 图A5 所示。场景1 中节点15 的电压均值较大,概率密度函数在1.05 以上的面积大于在场景2 的,即节点电压越上限的概率大于场景2,2 种场景电压越下限的概率几乎一致。相较于场景1,场景2 的概率密度函数更加集中。场景1 评估出的越限概率更高,与场景2 存在较大差异。 选取越限概率较为明显的线路2-3,分别计算在场景1 和场景2 下线路电流的概率密度函数,如附录A 图A6 所示。场景2 的线路电流均值高于场景1,且概率密度函数包围着0.8 以上的部分明显大于场景1。根据计算结果,场景2 的越限概率为0.913 4,接近1,较严重;场景1 越限概率为0.683 9。场景2 的电流容量越限概率较大,这种情况与节点电压场景1 越限概率大于场景2 的结论相反。 根据节点电压和线路电压越限概率分析结果,若不考虑光伏相关性,原本越限概率小的节点或线路可能被识别成薄弱环节,造成人力物力的浪费。因此,在识别过程中考虑光伏出力相关性有效提高了识别结果的精确性,该分析是必要的。 5.3.1 元件状态薄弱性评估 基于考虑出力相关性的重复潮流计算得到各个节点和线路最大供电能力,薄弱程度量化结果如附录A 表A3 所示。结果表明,尽管节点7 至节点18的电压越限概率完全不同,但各节点的供电薄弱程度却相同,节点26 至节点33 的供电薄弱程度依次递增。配网末端节点电压会随负荷增长不断降低,进行无功补偿后末端节点电压提升,可容纳更多的负荷增长,配电系统供电能力也随之提升。同时,容量越限线路的供电薄弱程度存在差异。尽管线路1-2 的越限概率最高,但与之相应的供电能力增长却是最低的,说明越限概率与供电能力的增长之间没有直接关系。 对比表1 的越限风险结果与附录A 表A2 的越限概率结果,越限概率与风险值呈现出的特征存在差异,越限风险在考虑薄弱程度后可更准确反映元件的状态薄弱性,如节点18 与节点28 电压越限概率仅相差0.006,而节点28 的电压越限风险是节点18 的2.6 倍;线路6-7 和线路10-11 电流越限概率仅相差0.001 2,而线路10-11 的越限风险是线路6-7 的7 倍。综合以上分析,所提出的元件状态薄弱性评估方法在考虑分布式电源出力相关性后,能很好地反映出元件的状态薄弱特征。 表1 元件状态薄弱性评估结果Table 1 Evaluation results of component condition weakness 5.3.2 元件结构薄弱性评估 基于提出的元件结构薄弱性评估指标评估节点结构薄弱性。如附录A 表A4 所示,同一节点各个指标值区间各异,不同节点同一指标却可能相同。节点8 至节点15 的节点度数DN,i相同,节点介数BN,i也十分相近,表明这些节点从度数和介数角度衡量在整个网络拓扑中的重要程度相近;而对于节点注入功率指标NP,i,节点8 远远大于节点15。同时,当节点的某一项指标为最大值时,另外几项指标有可能不是最大值,甚至非常小。 计算线路供电薄弱程度需要考虑N-1+1 后的最大供电能力评估结果,基于重复潮流计算对线路进行N-1+1 分析,结果见附录A 表A5。表2为线路结构薄弱性评估指标评估结果。线路结构薄弱性评估与节点结构薄弱性评估结果规律相同。对比表A4 和表2,在介数指标中,线路对应的指标值偏小,这与线路中电流值普遍偏小、而节点电压几乎全部集中在区间[0.95,1.05]一致。在度数指标中,线路度数在引入阻抗参数后赋予传统定义度数新的特征,例如由于节点6 的节点度数DN,i较大,线路6-7 的线路度数DL,u按传统定义计算值会明显大于线路8-9,但线路度数值却小于线路8-9,这也是区别于单纯考虑网络拓扑特征的地方。上述分析证明了单项元件指标仅能反映部分方面,所提评估指标不再受单个因素的影响导致判断片面,而是综合了电路拓扑结构和参数,提高了薄弱环节判断的准确性。 表2 线路结构薄弱性评估结果Table 2 Evaluation results of line structure weakness 采用修改的IEEE 33 节点配电系统,由光伏电站1 和光伏电站2 出力数据计算提出的状态薄弱性指标和结构薄弱性指标,作为训练集的输入。由于数据所限,仅将电压越限天数多的节点和电流重载天数多的线路作为实际工程中确定的薄弱环节。采用2018 年光伏出力数据进行潮流计算,统计1 年中各个节点电压和线路电流的越限天数,根据越限天数将薄弱环节分为短期(1 个月内)、季节性(1~4 个月)和长期(大于4 个月)3 种类型,类型统计结果作为训练集的输出。对训练集进行训练后,将基于2019 年光伏出力数据计算得到的各项指标作为样本输入,得到薄弱类型识别结果,并与2019 年统计数据进行对比,具体结果见附录A 表A6。其中,0代表非薄弱环节;1 代表短期薄弱环节;2 代表季节性薄弱环节;3 代表长期薄弱环节。 由附录A 表A6 数据可知,LSSVM 分类器对于薄弱环节的识别具有高精度,表明本文提出的考虑分布电源出力相关性的状态薄弱性评估指标和结构薄弱性指标可进一步考虑出力的相关性。将网络拓扑特点与分布式电源出力相关性的潮流相结合,识别结果与实际工程中依据统计结果确定的薄弱环节相差较小。 为了与传统的薄弱环节识别方法进行对比,将本文所提方法和文献[19]中基于层次分析法确定的各项指标权重及综合指标评估结果进行对比。由传统方法计算各个节点和线路的综合薄弱环节评估指标,并将综合指标由大到小排序。由于指标评估没有薄弱环节评判的标准,便将其按照大小顺序分为3 个区间,对应本文提出的3 种薄弱环节类型,统一用薄弱程度进行对比。传统薄弱环节识别方法的具体评估结果如附录A 表A7 所示。与本文所提方法的评估结果对比如图3 所示。以同样参数设置IEEE 51 节点系统(拓扑如图A8 所示),本文所提方法的识别结果与传统方法识别结果的对比如附录A图A9 和图A10 所示。 图3 薄弱节点识别结果Fig.3 Identification results of weak nodes 由附录A 表A7 的评估结果可知,综合指标排序通过相对大小来判定薄弱环节,仅能反映节点(线路)的薄弱程度。若综合指标最大值仍小于实际薄弱环节的指标值,则会识别出错,与实际情况相差甚远。通过图3 和附录A 图A7、图A9 和图A10 的对比可知,传统的综合指标评估从识别个数和识别程度2 个方面都与基于LSSVM 的识别结果存在较大差别。传统综合指标识别方法与实际工程中排查出的薄弱环节存在较大差别。而本文提出的基于LSSVM 的薄弱环节的识别方法提供了一种不依靠人为干预、对薄弱环节实现自动分类识别的思路。在对光伏出力相关性进行深入分析的同时,基于复杂网络理论改进评估方法,能够以较高的精度识别不同类型的薄弱环节,有效提升电网薄弱环节辨识的准确性。 针对中低压配电网薄弱环节识别问题,本文考虑分布式电源出力的相关性,对概率潮流分析、建立评估指标、薄弱环节综合识别进行了探索性研究。 1)提出了基于联合分布拒绝采样的出力相关性场景产生方法,结合蒙特卡洛法、半不变量与Cornish-Fisher 级数展开计算越限概率。 2)建立了考虑网架状态薄弱和结构薄弱两方面特征的评估指标体系。针对状态薄弱性,考虑了分布式光伏出力相关性场景下各元件对电能质量超标的影响程度,提出了基于重复潮流的薄弱程度量化方法,结合效用理论对节点和线路的越限风险进行评估。所提状态薄弱性评估方法可准确评估节点电压和线路容量越限风险;针对结构薄弱性,考虑分布式电源出力相关性改进了基于复杂网络的结构薄弱性指标。所提结构薄弱性指标结合了网络拓扑结构特点与考虑分布式电源出力相关性的潮流,实现了各个节点和线路的结构薄弱性量化。 3)提出了LSSVM 的薄弱环节识别方法,实现了元件级的薄弱环节识别和风险综合评估。所提识别方法与配电网生产实际相契合,能够以较高精度识别不同类型的薄弱环节,辅助实际工程调度决策,为配电网网架结构优化和可靠性提升提供指导意见。 后续工作将考虑多维分布式电源出力相关性,基于大数据进一步提升配网薄弱环节识别精度。 附录见本刊网络版(http://www.aeps-info.com/aeps/ch/index.aspx),扫英文摘要后二维码可以阅读网络全文。1.3 基于蒙特卡洛的概率潮流计算
2 元件状态薄弱性评估
2.1 考虑出力相关性的重复潮流


2.2 基于效用理论的薄弱程度量化


3 元件结构薄弱性评估




4 基于LSSVM 的主动配电网薄弱环节识别

5 算例分析
5.1 光伏出力相关性分析及场景产生

5.2 光伏出力相关性对配电网薄弱性评估的影响

5.3 考虑状态薄弱和结构薄弱特征的评估指标


5.4 主动配电网薄弱环节综合识别
6 结语

