脉冲噪声环境下的二维DOA估计
李苗苗,司伟建,颜卫忠
(1.哈尔滨工程大学信息与通信工程学院,哈尔滨 150001,黑龙江;2.哈尔滨工程大学先进船舶通信与信息技术工业和信息化部重点实验室,哈尔滨 150001,黑龙江;3.上海航天电子有限公司,上海 201800)
0 引 言
目前,阵列信号处理在声纳、5G 通信、雷达、智能天线等领域都得到了广泛的应用,这也表明了其在现代信号处理领域的重要地位。近几十年来,广大学者们对理想加性高斯白噪声条件下的DOA 估计进行了广泛且深入的研究,得到了以多重信号分类算法(multiple signal classification,MUSIC)和旋转不变子空间算法(ESPRIT)为代表的一系列DOA 估计算法。然而,在实际情况中,自然界的海杂波、地杂波、大气环境和雷达的散射回波都有可能呈现破裂和峰值,使得噪声环境表现出很强的脉冲特征。在这种情况下,基于理想噪声环境下所提出的算法性能会大幅度下降甚至失效。因此,研究人员为了解决这一问题提出了很多改进算法。文献[9]提出了基于共变的MUSIC 算法(ROC-MUSIC),该算法假定信号和加性噪声均服从于对称稳定(symmetric alpha stable ,SS)分布,且限制1<<2,但在实际中这种假设并不总是成立的。文献[10]提出了基于分数低阶矩的MUSIC 算法(FLOM-MUSIC),该算法适用于一般信号,不限制于SS 信号,应用范围更广。文献[11]将FLOM-MUSIC 进行改进并应用到均匀圆阵实现二维角度估计。文献[12]提出利用Lp 范数将迭代自适应(iterative adaptive approach,IAA)算法应用到脉冲噪声环境来估计波达方向。文献[13-14]将稀疏重构应用到脉冲噪声环境。然而,以上算法均存在着无法在低信噪比和高冲击噪声环境下实现准确的二维DOA估计的问题。文献[15]提出了基于相关熵的ESPRIT算法,但该算法无法实现自动角度匹配。文献[16]提出了基于广义协方差的GC-MUSIC算法,能够很好地抑制脉冲噪声,但需要大量的快拍数。本文提出了一种基于新型相关熵的旋转不变子空间算法(CBCMESPRIT),结合均匀圆阵来实现对信源方位角和俯仰角的联合估计,并通过大量仿真实验验证了所提算法能够在小信噪比、小快拍数和强脉冲噪声下实现准确的DOA估计。
1 阵列结构和信号模型
本文采用均匀圆阵(uniform circular array ,UCA)进行分析和仿真,UCA 的几何结构如图1 所示。假设个天线阵元是全向的,在平面内均匀分布在半径为的圆周上,设有(<)个相互独立的远场窄带信号入射到该均匀圆阵上,其所组成的信号空间为



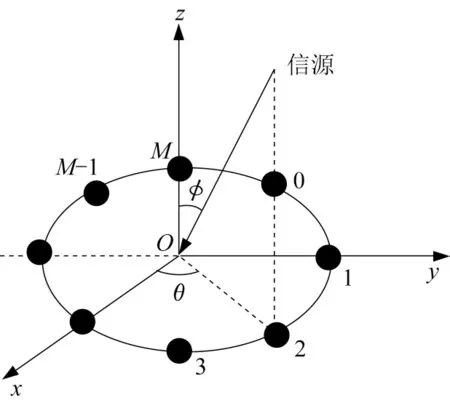
图1 均匀圆阵几何结构Fig.1 Geometrical structure of uniform circular arrays
脉冲噪声环境使用对称的Alpha 稳定分布(SS分布)建模,其特征函数定义如下:

式中:|()|表示信号的平均功率;表示噪声的分散系数。
2 基于相关熵的二维ESPRIT算法
2.1 相关熵函数

2.2 基于新型相关熵的协方差矩阵
若随机变量和均服从SS 分布且相互独立,则两个随机变量和基于新型相关熵的协方差矩阵定义为

式中:(0<<1)为抑制参数;为核宽度;引入抑制参数对随机变量和施加不同的抑制效果,式(14)可表示为

2.3 CBCM-ESPRIT算法
本文通过总结现有的DOA 算法,认识到实现DOA 的关键是修改传统的协方差矩阵以适应脉冲噪声环境,然后结合子空间技术实现DOA 估计。受相关性和高斯核函数在噪声先验参数未知的状态下就能很好地抑制脉冲噪声的启发,本文提出将高斯核函数对脉冲噪声的抑制作用应用到DOA 估计,并将此方法与UCA-ESPRIT 相结合,实现准确的二维DOA估计。假设所采用的信号与信号、信号与噪声、噪声与噪声之间都是独立的,入射信号个数小于阵元个数,依据均匀圆阵的阵列模型,波束空间由基于相位模式激励的UCA 波束形成器来产生。用本文所提出的相关熵协方差矩阵(CBCM)代替传统自相关函数,再通过对CBCM 进行实值特征值分解来获得信号子空间。
一个连续的均匀圆阵可以激励的相位模式最高阶数为≈(=2π/),第个模式的激励函数为d()=e(∈(0,2π))为式(2)所示的阵元放置角度,∈{-,-+1,…,-1,},因此共有'=2+1种模式。根据空间抽样定理,为了基本消除远场方向图公式中残留误差的影响,假设阵元数>2+6,在阵元位置对激励函数进行抽样可获得归一化权向量为


3 仿真结果及分析
本文的仿真实验均采用2 个等功率远场窄带独立信号入射到如图1 所示的10 阵元均匀圆阵上,并采用SS 分布的噪声,接收到的两组信号的仰角ϕ和方位角θ分别为[10°,20°]和[20°,120°],所有实验均独立进行500 次独立的蒙特卡洛仿真,并用DOA 的均方根误差(root mean square error,RMSE)和正确率作为评判算法性能的准则。本文进行的角度测量为二维角度,所以当方位角和仰角的估计值与真实值所对应的误差均在±1°以内时,计为1 次正确估计。若正确估计的次数为,则正确率为/500。同样地,均方根误差也由方位角和仰角的误差组合而成,其表达式为
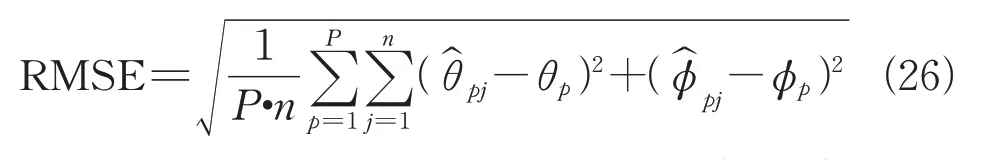

3.1 角度估计散点图分析
将本文所提出的二维CBCM-ESPRIT算法与二维ESPRIT、二维FLOM-ESPRIE 算法进行对比,均选取=1.2 作为脉冲噪声的特征指数,GSNR=6 dB,快拍数snaps设置为30。从仿真结果图2~4可以看出,在同样的较高冲击噪声和较低信噪比条件下,图2 所示的ESPRIT 算法几乎失效,估计的角度误差极大,图3 所示的FLOM算法所估计出的角度误差大概分布在3°左右,已经无法进行准确的DOA 估计,而图4 所示的CBCM-ESPRIT 算法的角度误差一直在1°左右。因此可以得出结论:本文所提出的CBCM-ESPRIT 算法能够有效地抑制脉冲噪声,与FLOM-ESPRIT 算法相比角度估计误差更小。

图2 ESPRIT角度估计散点图Fig.2 ESPRIT for angle estimation scatter graph

图3 FLOM-ESPRIT角度估计散点图Fig.3 FLOM-ESPRIT for angle estimation scatter graph

图4 CBCM-ESPRIT角度估计散点图Fig.4 CBCM-ESPRIT for angle estimation scatter graph
3.2 不同信噪比下的算法性能分析
将本文所提出的二维CBCM-ESPRIT 算法与ROC-ESPRIT、FLOM-ESPRIT、CRCO-ESPRIT 算法在不同GSNR 下的RMSE 和正确率进行比较。令GSNR 的值由−4 dB 逐渐增加到20 dB,且均选取1.2作为冲击噪声指数,快拍数snaps 设置为30。仿真结果如图5 和图6 所示,可以看出,在GSNR 较低的条件下,其他3种算法的正确率较低且均方根误差较大,无法正确判断信源方向,但CBCM-ESPRIT 算法的正确率始终保持较高且稳定增加,逐渐趋近于100%;该算法的RMSE 也始终小于其他3 种算法的RMSE,并稳定减小,逐渐趋近于0。由此说明本文所提出的新型的基于相关熵的CBCM-ESPRIT 算法比另外3 种算法更适合小信噪比环境,能保持较小的RMSE 和较高的正确率,更适合进行准确的DOA估计。

图5 4种算法在不同GSNR条件下的均方根误差Fig.5 Root mean square error of four algorithms under different GSNR conditions

图6 4种算法在不同GSNR条件下的正确率Fig.6 The accuracy of the four algorithms under different GSNR conditions
3.3 不同冲击噪声强度下的算法性能分析
将4 种算法在不同的冲击噪声指数值下的均方根误差和正确率进行比较。令值由1.2 逐渐增加到2.0,且设置GSNR 为6 dB,快拍数snaps 设置为30。仿真结果如图7 和图8 所示,可以看出在固定信噪比为6 dB 的条件下,随着冲击噪声指数的增加,4 种算法的性能均在逐渐提升。但在冲击噪声指数较小即冲击噪声较强的情况下,本文所提CBCM-ESPRIT 算法的RMSE 明显低于CRCO-ESPRIT、FLOMESPRIT、ROC-ESPRIT 算法的RMSE,且保持着较高的正确率。随着冲击噪声指数的增加,本文所提算法RMSE 逐渐趋近于0,正确率逐渐趋近于100%。本实验说明本文所提出的基于新型相关熵协方差矩阵的CBCM-ESPRIT 算法比另外3 种算法更适合强脉冲噪声环境,能保持较小的RMSE 和较高的正确率,更适合进行准确的DOA估计。

图7 4种算法在不同α值下的均方根误差Fig.7 The root mean square error of the four algorithms at different alpha values

图8 4种算法在不同α值下的正确率Fig.8 The accuracy of the four algorithms at different alpha values
3.4 不同快拍数下的算法性能分析
将4种算法在不同快拍数下的均方根误差和正确率进行对比,冲击噪声指数值设置为1.2,GSNR设置为6 dB,快拍数snaps由10逐渐增加到100。图9~10分别表示4种算法在不同快拍数下的RMSE和正确率的对比情况,可以看出当信噪比和冲击噪声特征指数值固定时,快拍数由10增加到100的过程中,CBCM-ESPRIT算法的RMSE 始终低于CRCO-ESPRIT、FLOMESPRIT、ROC-ESPRIT算法的RMSE,且正确率始终高于以上3 种算法的正确率,在快拍数小于50 的时候CBCM-ESPRIT算法的优势更为明显。本实验说明本文所提出的CBCM-ESPRIT算法在小快拍数情况下也能保持较低的均方根误差和正确率,更适合在小快拍数环境下实现准确的DOA估计。

图9 4种算法在不同快拍数下的均方根误差Fig.9 The root mean square error of the four algorithms at different snapshots

图10 4种算法在不同快拍数下的正确率Fig.10 The correct rate of the four algorithms in different number of snapshots
4 结束语
本文提出了一种基于新型相关熵协方差矩阵的二维DOA 估计算法,该算法将传统DOA 估计中的协方差矩阵替换成新型相关熵矩阵,再通过结合UCA-ESPRIT 算法来实现在小信噪比、小快拍数、强冲击噪声环境下的二维DOA 估计。仿真结果表明,与CRCO-ESPRIT 算法相比,本文所提的CBCM-ESPRIT 算法能够实现在更低信噪比、更强冲击噪声、更小快拍数环境下准确的DOA 估计。与传统的基于分数低阶矩的算法相比,除了具有以上优势外还无需获取冲击噪声特征指数的先验信息,并且放宽了信号和噪声中对-stable 的约束条件。文中比较了这几种算法在SS 噪声环境下的DOA 估计均方根误差和正确率,结果表明,CBCM-ESPRIT 算法的估计性能明显优于CRCO-ESPRIT 算法、FLOMESPRIT算法和ROC-ESPRIT算法的估计性能。

