基于Levenberg-Marquardt算法的材料温度相关热物性参数辨识
窦怡彬,陈 昂,陆云超,刘陆广,李宗阳
(上海机电工程研究所,上海 201109)
0 引 言
随着导弹向着高速、远程的方向发展,气动加热及热防护设计已经成为高超声速飞行器研制过程中一项重要且必不可少的工作。在方案设计阶段,通过对弹体结构大面积部位开展传热分析,并根据得到的温度响应给出初步的防热方案。结构的温度响应受材料热物性参数影响较大,而这些参数往往难以获得或者信息不全面、不准确,只能利用类似材料的参数近似求解。因此需要开展物性参数辨识研究,为后续防热设计和热传导模型修正提供依据。
热传导逆问题(inverse heat conduction problem,IHCP),是指利用实验手段测得物体内部或边界上某点或某些点上的温度及其随时间的变化历程,通过求解传热微分方程来反演物体边界热流、材料热传导系数或物体内部的热源分布等参数。国内外许多学者提出了大量的逆问题辨识方法并应用于不同的工程领域。钱炜祺等提出了基于灵敏度方法和顺序函数法的热导率辨识和表面热流辨识方法。何开锋等总结了高超声速飞行器气动力/热参数辨识国内外研究现状和辨识方法。周宇等基于最速下降法研究了耦合传导/辐射情况下的一维半透明材料的传热系数和表面热流辨识问题。朱燕伟详细研究了蜂窝增强低密度烧蚀材料的热物性参数和表面热流辨识问题。Duda给出了瞬态多维热传导逆问题的一般求解方法。Yang等研究了刹车盘表面热流辨识问题。Xie等研究了气凝胶材料吸热反应参数及物理参数的反演问题。Kamalpreet 等进行了热成型模具淬火加热阶段超高强度钢比热容的反演分析。
热传导逆问题主要有两类求解方法:基于梯度的方法和基于随机的方法。随机方法主要指随机智能优化算法,这类方法全局最优求解能力强,但是计算量巨大且辨识参数数量不能过多。基于梯度的方法具有求解精度高、速度快等优点,但是容易陷入局部最优解。L-M 算法是一种基于梯度的算法,在热传导逆问题中被广泛应用。Cui对L-M 算法中不同形式阻尼因子对计算收敛性和收敛时间进行了研究,提出了基于残差的阻尼因子确定方式。
综合国内外热传导逆问题研究可知,在热物性参数研究方面,大部分研究集中在热传导的反演上,对于同时反演热导率和比热容的研究相对较少。周宇基于伴随方程方法对热物性参数按温度区间离散为不同的常数进行优化辨识,其他相关文献对热物性参数的研究往往以第二类边界条件为例,和工程研制中常用的石英灯加热试验或者电弧风洞试验中的耦合边界条件有出入,无法直接使用。本文以L-M 算法为基础,推导了任意截面积一维固体热传导数学模型,耦合了第二类/第三类/黑体辐射边界条件,并给出了隐式求解过程。其中热物性参数定义为随温度变化的多项式函数,给出了热导率和比热容辨识的整个过程,并通过2 个算例验证了本文方法的有效性。本文的方法可以适用于石英灯加热试验或者电弧风洞试验,拓展了温度相关热物性参数辨识方法的使用范围。
1 计算模型
1.1 一维热传导数学模型
任意面积下一维固体热传导方程的数学表达式为
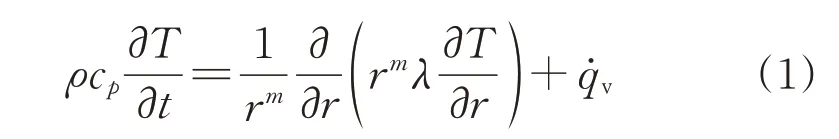
式中:、c、、、̇、和分别为材料密度、比热容、定压条件、热导率、内热源、温度和一维方向坐标;取0、1和2分别对应笛卡尔坐标系、圆柱坐标系和球坐标系。采用有限体积法对一维结构进行离散,具体如图1所示。
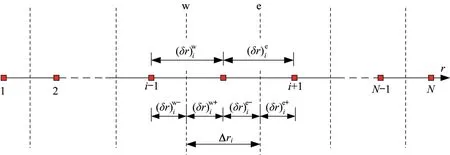
图1 控制体示意图Fig.1 The diagram of control volume


式中:卡方函数()为实值有界函数,为待辨识参数向量;σ是温度测量误差;是测量误差倒数构成的协方差矩阵。式(17)是非线性优化问题,需要采用迭代方法求解得到。
1.2 Levenberg-Marquardt算法
Levenberg-Marqurdt 算法被广泛用于求解线性病态问题,该算法在最优点附近退化为Gauss-Newton法,在远离最优点的时候具有最速下降法的特点,其具体表达式为
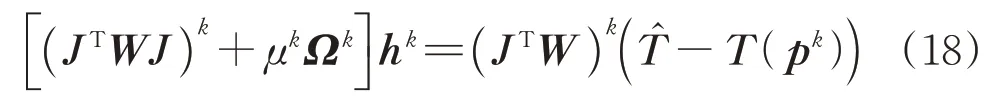
式中:上标表示迭代步数;=∂∂为雅各比矩阵;为对角矩阵;为阻尼因子;h为增量步长。对角矩阵的目的是通过使得矩阵对角占优来抑制由于逆问题的病态特性导致矩阵近似奇异而引起的数值振荡和不稳定。不同版本L-M 方法的差别主要体现在对角矩阵和阻尼因子的选择上,本文采用如下形式矩阵

图2给出了基于L-M算法的热物性参数逆问题计算流程图。
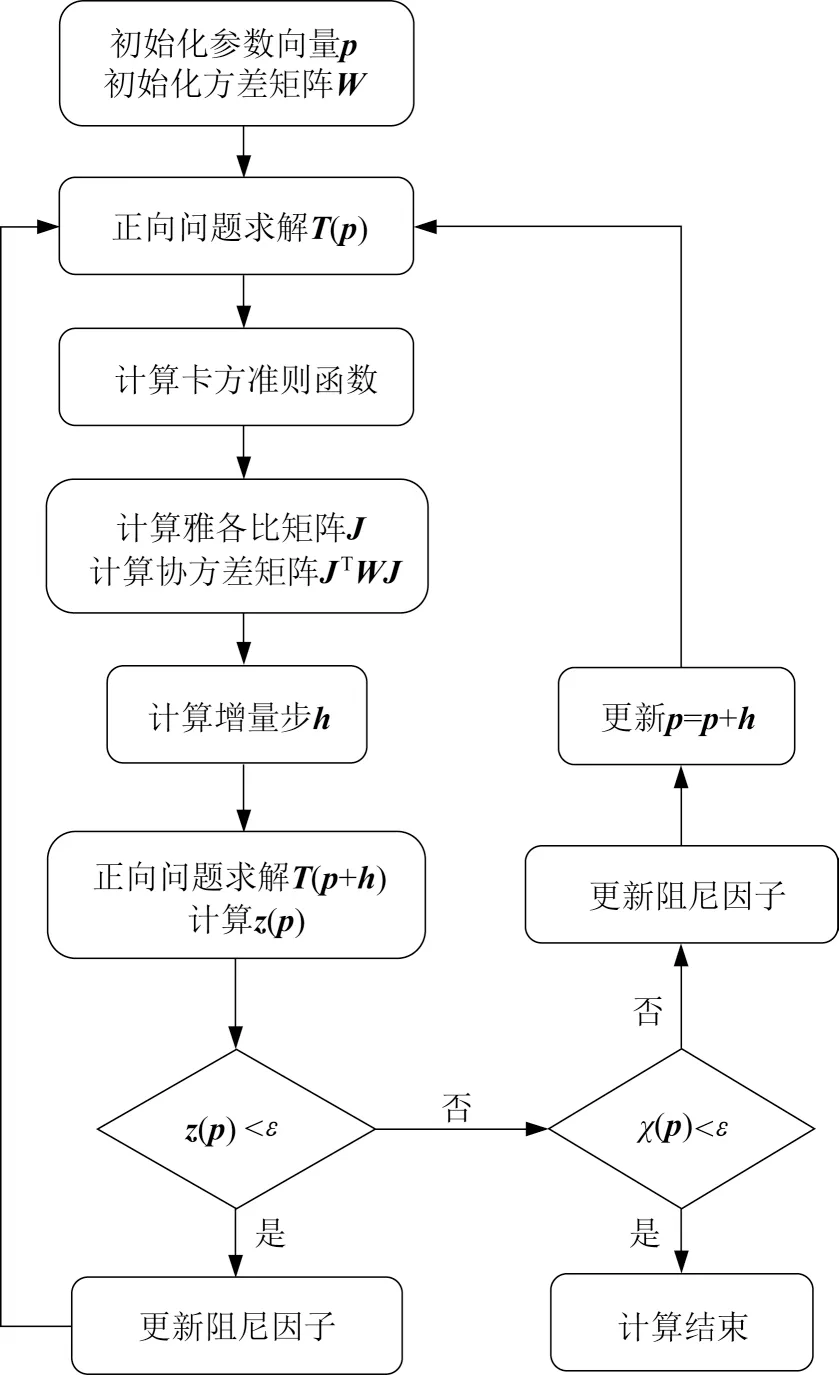
图2 逆问题求解流程图Fig.2 Flowchart of solving IHCP
辨识参数的渐进标准差可以通过协方差矩阵来估计,协方差矩阵可以用近似Hession 矩阵来表示

1.3 置信区间分析
采用F-检验方法确定辨识参数的置信区间,在误差曲面上最优辨识参数对应误差面上的最小值,每次固定一个参数p,其他参数可调节。对模型采用L-M算法进行优化得到新的卡方函数,建立如下分布函数
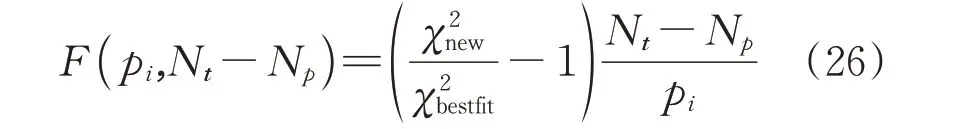
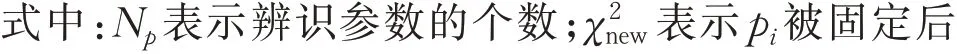

2 数值仿真及结果分析
2.1 有噪声状态热传导率逆问题
以TC4材料为例,通过查阅手册得到该材料的热传导系数如表1 所示,密度=4 440 kg/m。对一块4 mm 厚的TC4 钛合金板材,对外表面施加150 kW/m热流,计算试片背温。对背温数据增加0均值白噪声,其具体表达式为
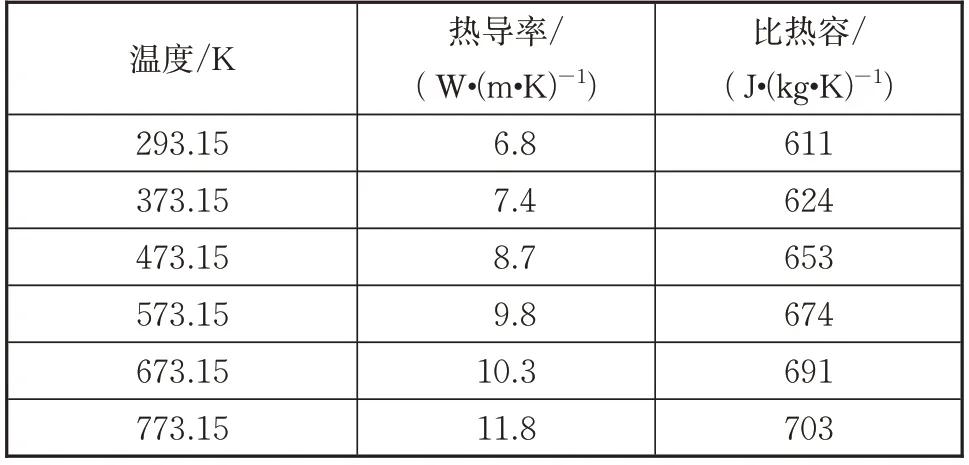
表1 TC4热物性参数Tab.1 Thermophysical parameters of TC4
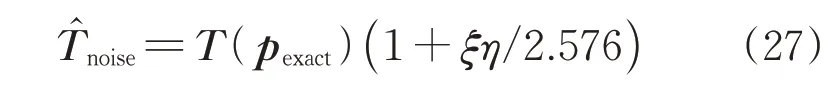
式中:为测量误差;为[-1,1]内正态分布的随机数;̂为含测量噪声的温度。计算中取=0.01/0.03/0.05。不同的测量噪声会导致辨识结果随机散布,辨识结果散布程度可以通过多次重复试验获得。对每一个取值构造50组含有不同测量噪声的温度数据进行辨识,图3给出了其中一组温度数据。
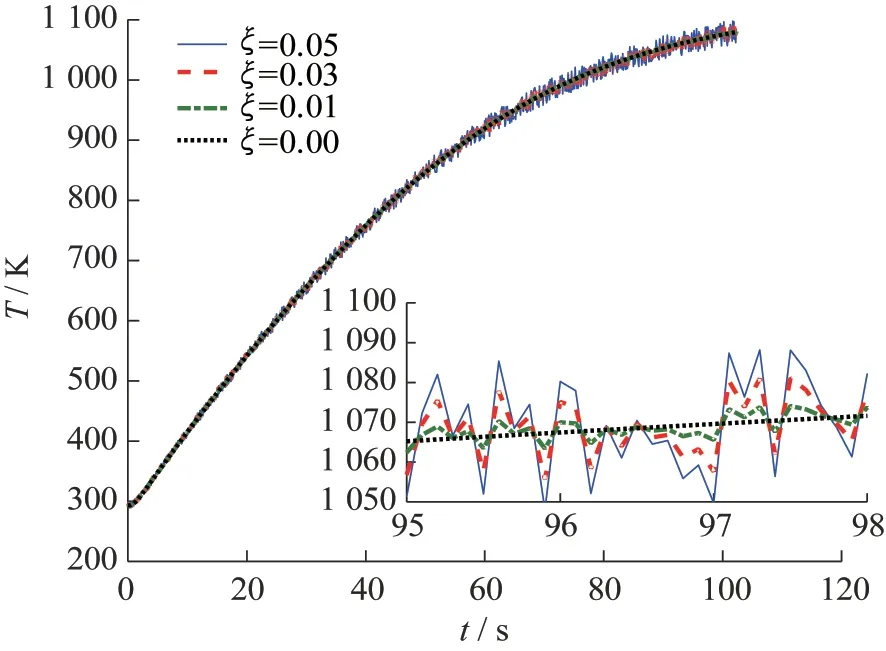
图3 不同随机测量误差下的温度Fig.3 Temperatures with different random measurement errors
表2 给出了不同下辨识参数的平均值,其中最大相对误差为1.6%,该误差较小,可以认为参数辨识结果是无偏的。表3 给出了辨识结果的偏离程度估计,通过对辨识结果计算样本标准差和平均渐进标准差,反映出参数估计的不确定度。整体上平均渐进标准差和样本标准差趋势相同,和具有较明显的正相关性,随着增大而增大。而平均值相对误差和之间没有非常明显的线性相关性。图4 和图5 分别给出了=0.01 状态下热导率辨识结果和渐进标准误差分布。
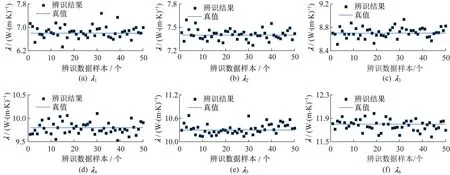
图4 热导率辨识结果(ξ=0.01)Fig.4 Identified thermal conductivities(ξ=0.01)
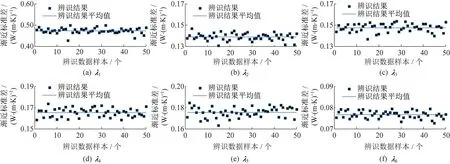
图5 热导率辨识结果渐进标准误差(ξ=0.01)Fig.5 Asymptotic standard errors of identified thermal conductivities(ξ=0.01)
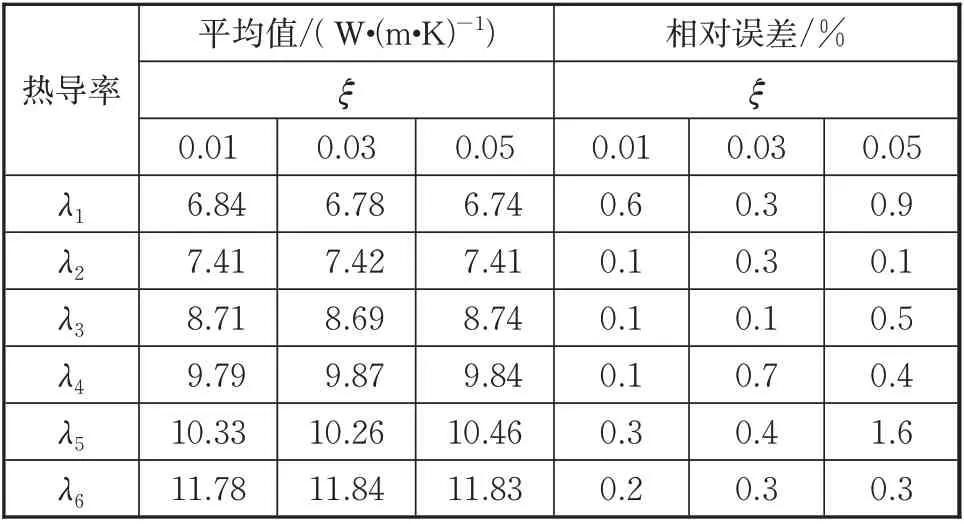
表2 热导率辨识结果和相对误差Tab.2 Identified thermal conductivities and errors
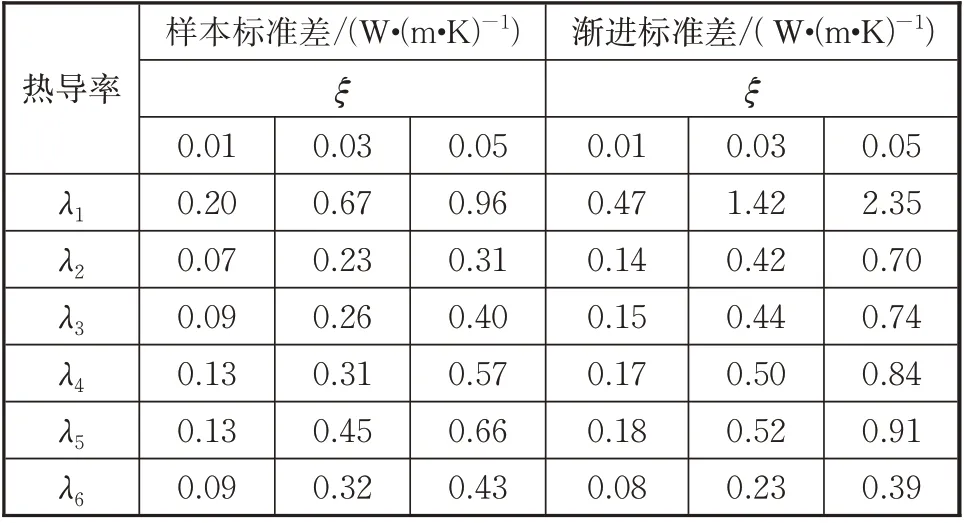
表3 热导率辨识结果的标准差和渐进标准差Tab.3 Standard deviations and asymptotic standard errors of identified thermal conductivities
实际测试中往往只有一组试验的测量数据,无法通过多次平均得到较为准确的辨识结果,这时需要对辨识结果进行置信度分析或者给出指定置信度下的参数区间。从=0.05 构造的响应数据中取其中一个响应结果,采用F-检验方法分析其68%和95%置信区间,并和1 倍渐进标准差下的置信区间结果进行比较,结果如表4 所示。可以发现:1 倍渐进标准差下的置信区间和F-检验68%置信区间较为接近。
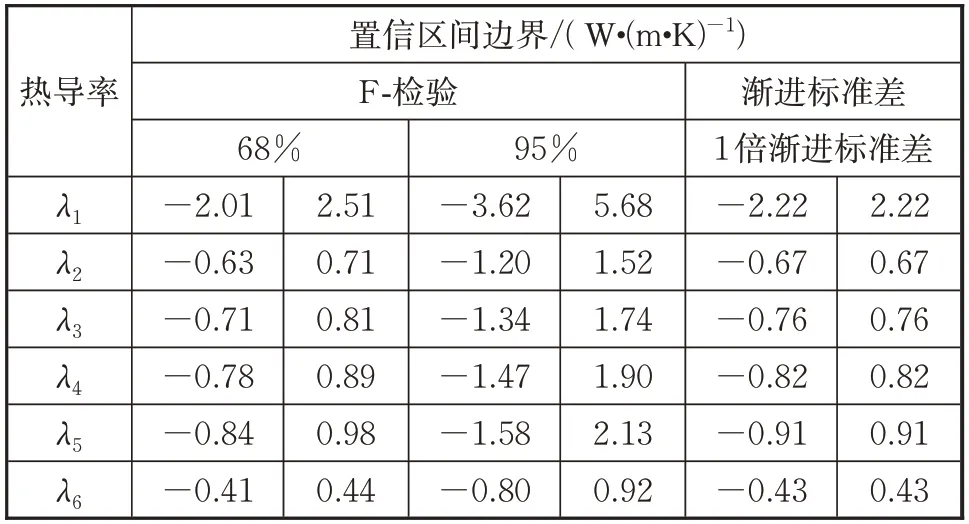
表4 热导率置信区间Tab.4 Confidence interval of identified thermal conductivities
图6 给出了热导率辨识结果和置信区间,采用F-检验得到的68%、95%置信区间以及1 倍渐进标准差得到的置信区间都将真值包括在区间范围内。从表4和图6可以看出:6个热导率参数中的不确定度最大,且不确定度的非线性最强。这主要是因为本文用的辨识数据为阶跃响应函数,其温度响应值落在和对应的温度区间范围内的情况较少导致辨识结果的不确定度较大。F-检验和渐进标准差都可以反映出辨识参数的不确定度,但F-检验还可以反映出不确定度的非线性程度,即置信区间关于辨识结果的不对称程度。
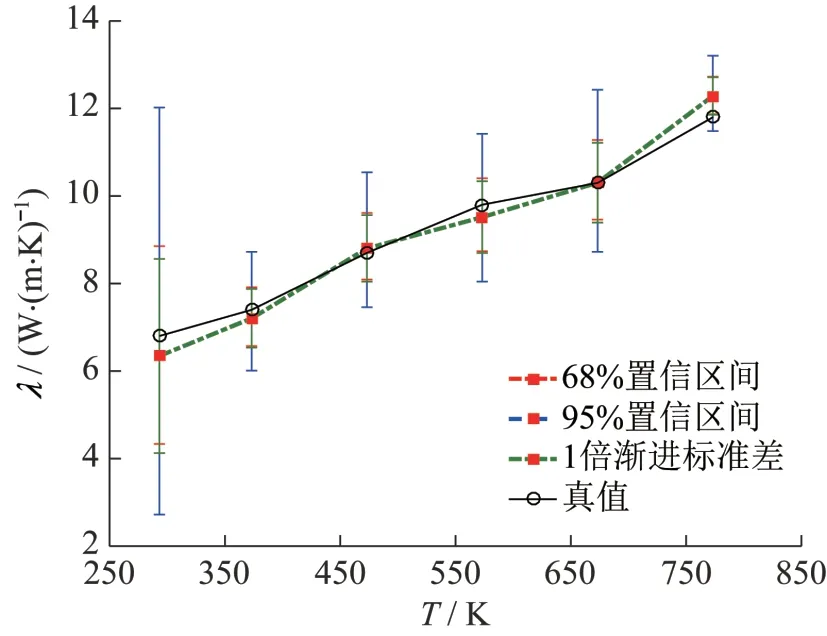
图6 辨识结果和置信区间Fig.6 Identified results and confidence interval
2.2 有噪声状态热传导率和比热容逆问题
2.1节对热导率辨识进行了研究,本节主要考核程序同时对热导率和比热容进行辨识的能力。仍然以TC4材料为例,对一块4.0 mm厚的TC4钛合金板材,在其外表面施加150 kW/m的热流,持续时间100 s,以试片背温作为辨识输入参数,同时辨识热导率和比热容随温度变化关系。以常温状态辨识得到的材料参数作为计算初始条件,常温状态下辨识得到热导率为8 W/(m·K),比热容为660 J/(kg·K)。以=0.01时的50组数据进行辨识,得到的辨识结果如表5和表6所示。可以看出,~和c这5个参数的渐进标准差与辨识参数的比值较大(即不确定度较大),且相对误差也较大,说明这些参数之间的相关性较强,可辨识性较低,属于不可辨识参数。
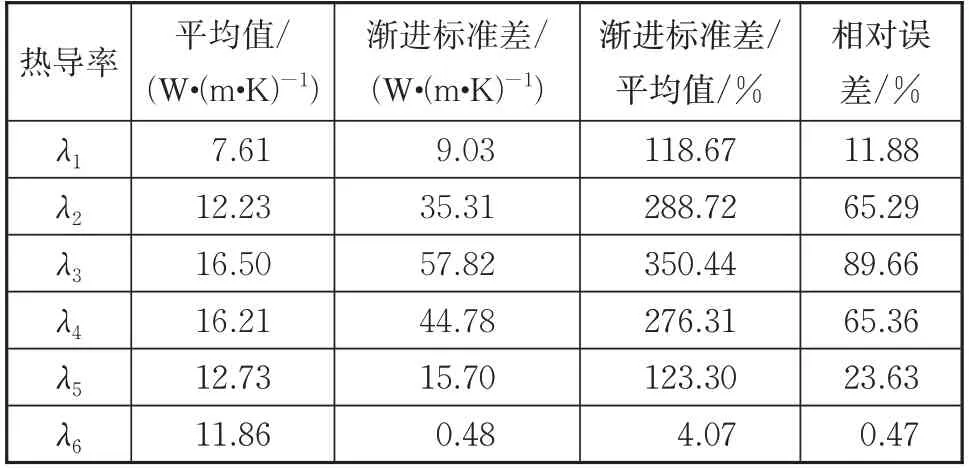
表5 热导率辨识结果和误差Tab.5 Identified thermal conductivities and errors
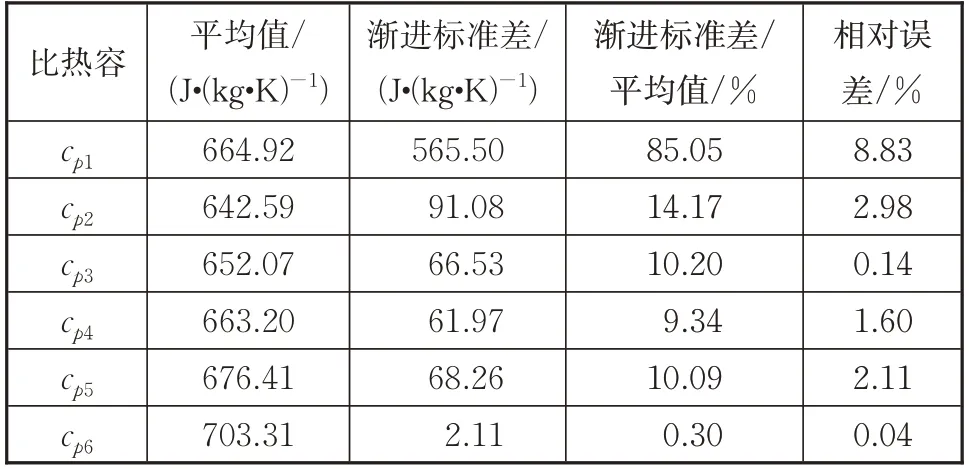
表6 比热容辨识结果和误差Tab.6 Identified specific heat capacities and errors
去掉上述5个不可辨识参数后,重新进行计算,得到辨识结果和相对误差如表7和表8所示。热导率平均值相对误差最大为13.7%,比热容平均值相对误差最大为2.22%。整体来看比热容的辨识结果精度更高,这主要是因为的可辨识性相比于比热容参数来说更差,对的辨识引起热传导率参数辨识结果整体误差增大。
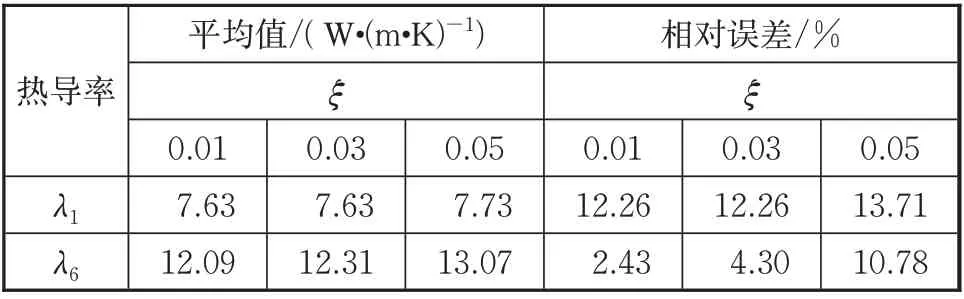
表7 热导率辨识结果和误差Tab.7 Identified thermal conductivities and errors
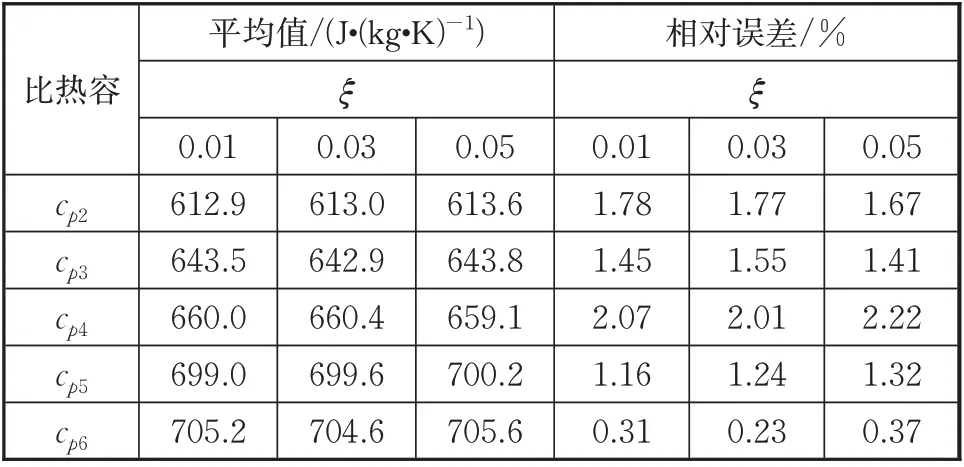
表8 比热容辨识结果和误差Tab.8 Identified specific heat capacities and errors
表9和表10 则给出了辨识结果的标准差和渐进标准差,随着数据噪声水平的增大而增大,反映了参数的不确定度和具有较明显的正相关性。而平均值相对误差和之间没有非常明显的线性相关性,这点和只辨识热导率得到的结论一样。
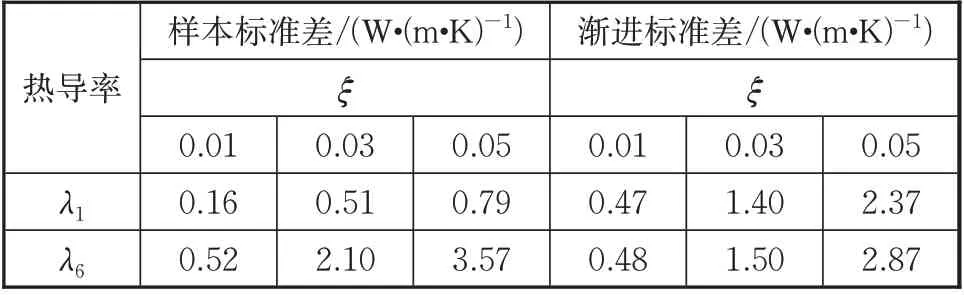
表9 热导率辨识结果的标准差和渐进标准差Tab.9 Standard deviations and asymptotic standard errors of identified thermal conductivities
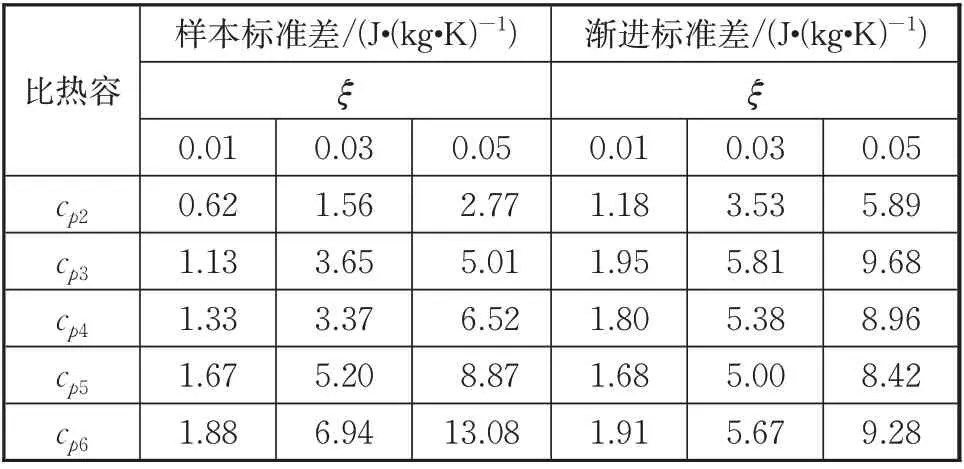
表10 比热容辨识结果的标准差和渐进标准差Tab.10 Standard deviations and asymptotic standard errors of identified specific heat capacities
图7 和图8 是噪声水平=0.01 时的参数辨识结果和渐进标准差分布结果(不可辨识参数赋值情况为热导率赋值8 W/(m·K),比热容赋值660 J/(kg·K))。对比真值可以看出辨识结果是有偏的。图9 是噪声水平=0.01 时的参数辨识结果(不可辨识参数赋真值),平均值相对误差分别为0.25%、0.71%、0.000 4%、0.009 6%、0.006 1%、0.027 7%和0.036 3%,为无偏估计。由此可见,是不可辨识参数的赋值误差导致了估计结果的有偏。2.1 节中也是因为给比热容赋值为真值才保证了热导率辨识结果是无偏的。
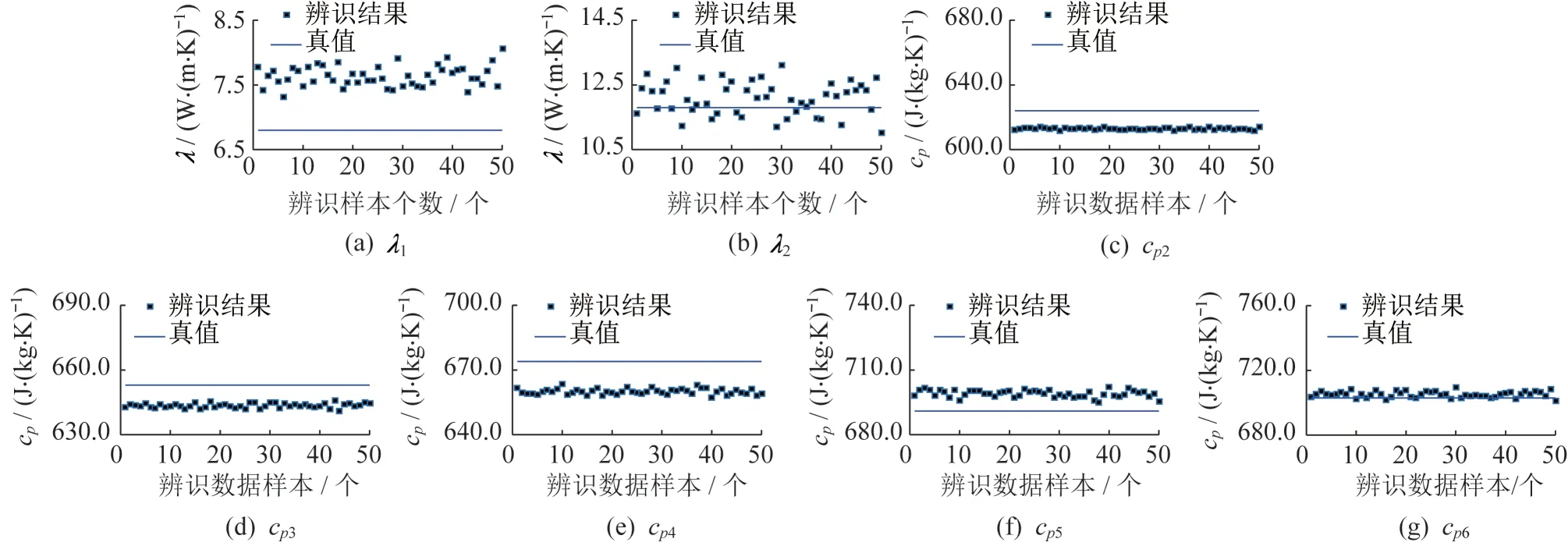
图7 热导率和比热容辨识结果(ξ=0.01)Fig.7 Identified thermal conductivities and specific heat capacities(ξ=0.01)
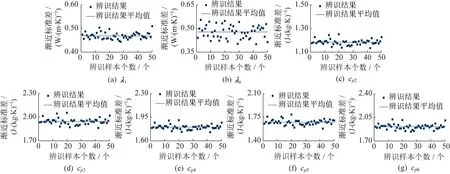
图8 热导率和比热容辨识结果渐进标准误差(ξ=0.01)Fig.8 Asymptotic standard error of identified thermal conductivities and specific heat capacities(ξ=0.01)
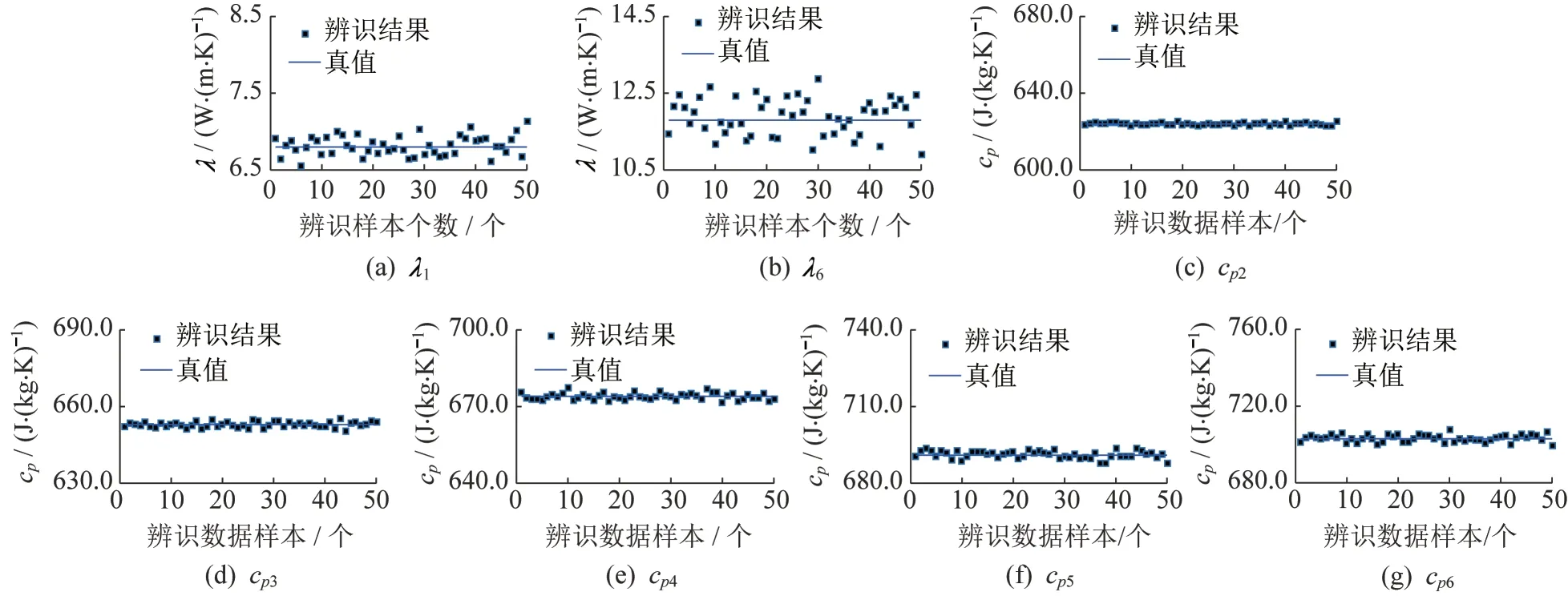
图9 热导率和比热容辨识结果(ξ=0.01,不可辨识参数赋真值)Fig.9 Identified thermal conductivities and specific heat capacities(ξ=0.01,unidentified parameters assigned true value)
取=0.01时的一组数据进行辨识,得到辨识结果并用F-检验方法计算置信区间,结果如表11~12、图10~11所示。辨识结果为有偏估计,置信区间无法将真值包括在区间范围内。68%置信区间和1倍渐进标准差置信区间基本相同。同时热导率参数的不确定度比比热容的不确定度更大。但是所有参数的不确定度的非线性程度都较低,特别是比热容参数基本没有体现出非线性。
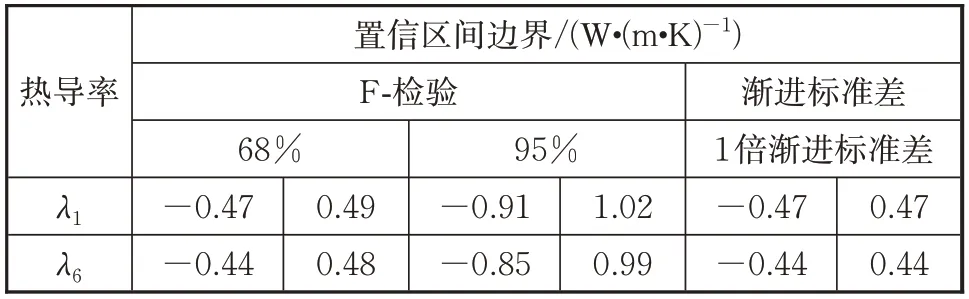
表11 热导率置信区间Tab.11 Confidence interval of identified thermal conductivities
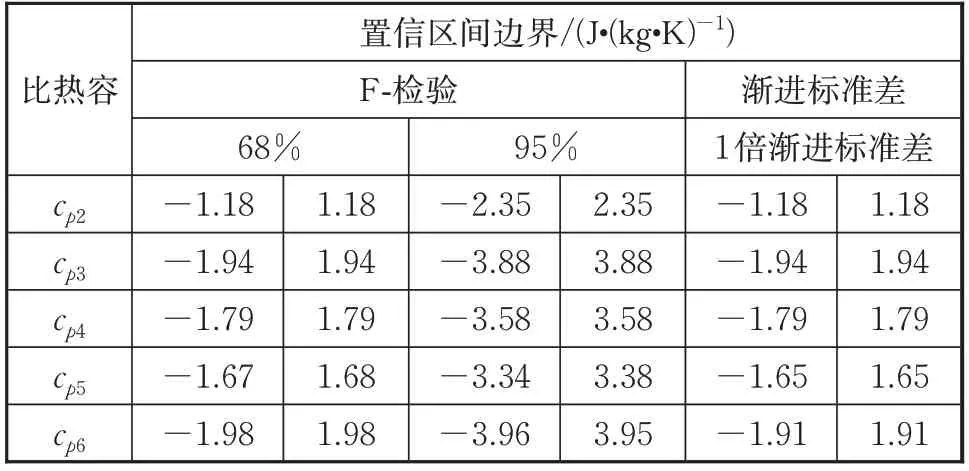
表12 比热容置信区间Tab.12 Confidence interval of identified specific heat capacities
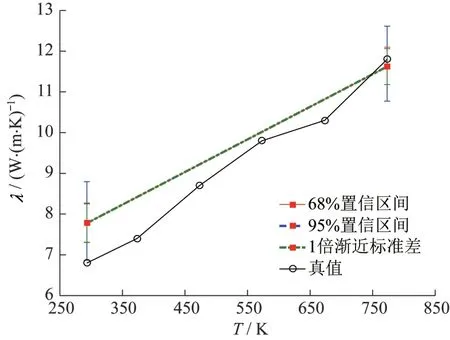
图10 热导率辨识结果和置信区间Fig.10 Identified results and confidence interval of thermal conductivities
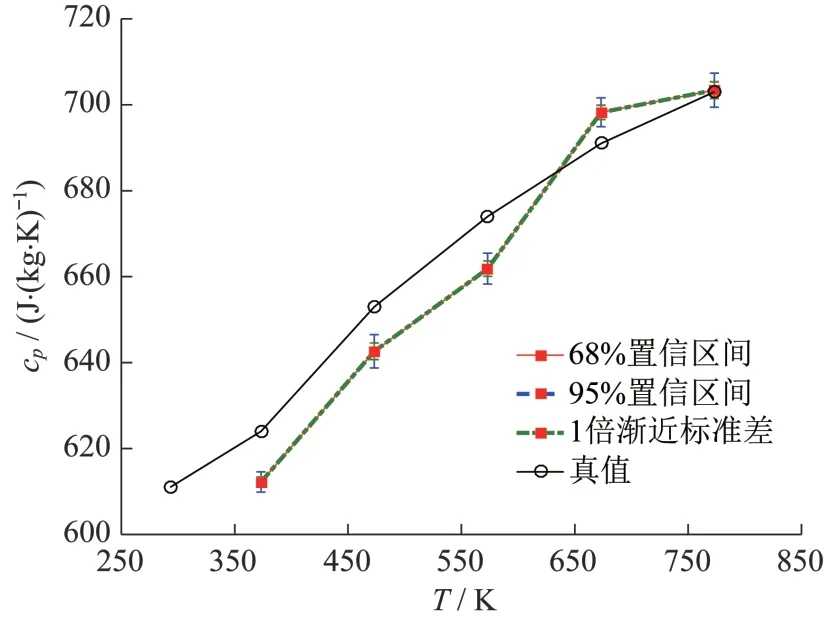
图11 比热容辨识结果和置信区间Fig.11 Identified results and confidence interval of specific heat capacities
3 结束语
本文推导了基于耦合边界条件的一维热传导方程,基于Levenberg-Marquardt(L-M)算法给出了一维热传导方程中热物性参数辨识方法,并通过两个数值算例验证了本文方法的可行性和准确性,形成以下结论:
1)对于L-M算法辨识热物性参数,固定不变的参数或者不可辨识参数的赋值会影响辨识结果的精度,即当固定参数赋值为真值时,其余参数辨识结果是无偏的;当固定参数赋值不为真值时,其余参数辨识结果是有偏的。
2)辨识结果的平均值和真值的相对误差与噪声水平没有明显的正相关性;辨识参数的样本标准差和平均渐进标准差随着噪声水平的增大而增大,即辨识结果的不确定度与噪声水平具有明显的正相关性。
3)只辨识热导率情况下,6 个热导率参数中的不确定度最大,不确定度的非线性程度最高。这主要是因为本文用的辨识数据为阶跃响应函数,其温度响应值落在和对应的温度区间范围内的情况较少导致辨识结果的不确定度较大。
4)对于同时辨识热导率和比热容的情况,热导率和比热容参数之间存在一定的相关性,导致部分参数不可辨识。
5)对于同时辨识热导率和比热容的情况,比热容辨识结果精度高于热导率辨识结果精度,这主要是因为热导率的可辨识性更差,更大的不确定性增大了参数辨识结果的误差。
6)使用F-检验方法计算辨识结果的置信区间可以有效反映出辨识结果不确定度的非线性程度,即置信区间关于辨识结果是不对称的,而1 倍渐进标准差方法得到的置信区间则无法反映这种特征。
后续可继续研究参数的可辨识性,确认最优的辨识参数个数;研究辨识输入信号和参数可辨识性的关系,设计最优辨识信号。

