具有回弹复位功能易裂盖的结构设计及力学性能研究

贾米芝，徐澧明，林 楠，南博华，王 坤，蔡登安，周光明

（1.南京航空航天大学机械结构力学及控制国家重点实验室，江苏南京 210016；2.上海机电工程研究所，上海 201109；3.上海航天设备制造总厂有限公司，上海 200245）

0 引 言

箱式发射技术在导弹发射系统中运用广泛。对于舰载和潜载飞航导弹，贮运发射箱是箱式导弹发射系统的基本组成部分，而发射箱盖作为导弹贮运发射箱中关键部分，其设计必须满足：在导弹存储和运输中，发射箱盖具有一定的密封性以防止发射装置内的惰性气体外泄，保护弹头不受损伤；当导弹发射时，需能承受相邻导弹发射时的燃气冲击；在一定的箱内燃气压力或弹头顶破力下能迅速打开，保证导弹顺利发射。

目前导弹发射盖有机械盖、爆破盖和复合材料易裂盖3 种形式，其中机械盖和爆破盖在不同程度上存在结构复杂、质量大、反应慢、保养和维修成本高等缺点。而复合材料易裂盖则由于质量轻、刚度和强度高、可设计性强等优点逐渐成为国内外导弹发射箱盖研究的热点。

为提高战斗条件下的可靠性，缩短反应时间提高发射速度，国内外已研制了多种破坏形式的复合材料易裂盖。Doane采用玻璃纤维和环氧树脂设计了一种穿透式复合材料易裂盖，提出在弹头接触区域预留薄弱区，利用导弹发射时弹头冲击易裂盖使其破碎，从而使导弹顺利发射。Kam等设计了一种利用导弹发射时在发射筒中产生高压燃气使盖体以预定的四瓣形式破坏的复合材料易裂盖，但由于薄弱区为纯树脂连接，且盖体较厚，减重效果不明显。Zhou等设计了一种局部非分裂薄弱区的圆帽形易裂盖，实现了易裂盖的定向抛出功能。Cai等利用Riemann 算法建立了圆帽形易裂盖气流冲破的动态分析有限元模型，分析了薄弱区位置和加强布条的长度对冲破压力的影响。卓毅等通过设计弱化槽并改变槽参数，配合泡沫材料特性使设计的环氧泡沫塑料易裂盖达到了其承压要求与破坏后的碎片控制，最后通过试验验证了该易裂盖结构设计的合理性。安庆升等设计了一种冲破式异型结构易裂前盖，该易裂盖具备良好的综合性能，且能满足该型号易裂盖设计要求。徐澧明等设计了一种凹槽式薄弱区结构的平面整体冲破式易裂盖，并分析了设计参数对易裂盖性能的影响。李文龙等提出了一种复合材料多瓣易裂盖薄弱区的结构设计方法，并制作了易裂盖实物进行试验，达到了减轻易裂盖分离体质量的效果。段苏宸等利用动网格技术进行了易裂后盖开启及运动过程的燃气流场仿真，仿真计算结果与试验数据一致。

随着导弹垂直发射系统的发展，发射箱的安装越来越密集，上述发射箱盖在发射时的抛出体在导弹尾焰的加速下，可能会对相邻箱盖产生冲击损伤。因此，基于发射箱盖安全性的考虑，提出了发射时无抛出碎块和自动关盖的新要求。本文设计了一种具有回弹复位功能的新型分瓣顶破式易裂盖，并对其进行了试验研究和有限元数值分析。结果表明，本文设计的易裂盖不仅具有传统易裂盖的性能，而且可以成功实现发射时无抛出碎块和自动关盖的功能。本文的回弹设计方案为易裂盖的安全性设计提供了新思路。

1 易裂盖结构和材料

易裂盖整体结构如图1所示，设计为平面分四瓣的形式，按各区功能可划分为5部分：法兰框、分瓣薄弱区、根部薄弱区、分瓣子盖和功能层。分瓣子盖和法兰框由玻璃纤维增强环氧树脂基复合材料板切割而成。分瓣子盖之间、分瓣子盖与法兰框之间均用AB胶胶接，其胶接区域分别为分瓣薄弱区和根部薄弱区。本文中试制的盖体铺层层数为10 层，中间为8 层0.4 mm（实测0.35 mm）厚的0°/90°双向高强玻璃纤维布，上下两侧各有一层0.2 mm厚的0°/90°双向高强玻璃纤维布。铺层顺序为［（0°/90°）/（±45°）］的准各向同性铺层。

由于功能层需具备回弹复位的作用，因此其材料的选取至关重要。该材料既要可靠地连接分瓣子盖与法兰框，保证顶破后无抛出体飞出，又能在易裂盖受弹头顶破时发生弹性弯曲，在导弹飞出后依靠自身刚度回弹复位。考虑到玻璃纤维双向平纹布在浸胶固化后具有合适的刚度和强度，在弯曲一定角度后仍可恢复变形，因此可采用浸胶后的一层或几层平纹布作为功能层。在盖体根部薄弱区的回形位置，通过在功能层与盖体之间设置脱粘区域，使二者之间失去粘接力，以便易裂盖顶破时功能层在此脱粘区域能够发生弯曲大变形，并在导弹飞出后依靠自身刚度回弹复位。如图1（a）所示，易裂盖的功能层位于盖体正面，在制作过程中，将功能层沿与分瓣薄弱区重合的切割线割开，选择脱模布作为脱粘区域处的隔离材料。

图1 易裂盖结构Fig.1 The structure of fissile cover

为控制盖体撕裂方式、顶破力和加强气密性能，在正面分瓣薄弱区和反面根部薄弱区处分别设置了加强布。对于分瓣薄弱区，如图1（a）所示，从中心到根部将之划分为A、B、C 3个区域，通过在此3个区域粘贴不同的加强布，达到由中心到根部强度呈增强趋势的效果，以确保顶破工况下，盖体首先在中心破坏，然后向根部扩展。对于根部薄弱区，如图1（b）所示，贴有回形加强布，通过控制回形加强布的层数及与分瓣子盖的粘接宽度来实现对根部强度和气密性能的调整。

本文试制的易裂盖相关尺寸描述如图2所示。分瓣薄弱区胶层宽度为，其A、B、C 3 个区域加强布的长度分别为、、，加强布宽度均为20 mm；功能层脱粘区域宽度为，在分瓣子盖一侧的长度为；根部薄弱区胶层宽度为，其回形加强布的宽度为，长度均为280 mm，布条与分瓣子盖搭接长度为；分瓣子盖根部边长为；易裂盖直径为。易裂盖实物如图3所示，其中正面粘贴了一层功能层，A 和B 区粘贴了1 层0.2 mm 厚加强布，C 区粘贴了2 层0.2 mm 厚加强布，反面根部薄弱区粘贴了1 层0.2 mm 厚的回形加强布。易裂盖试件的详细尺寸数据如表1所示。

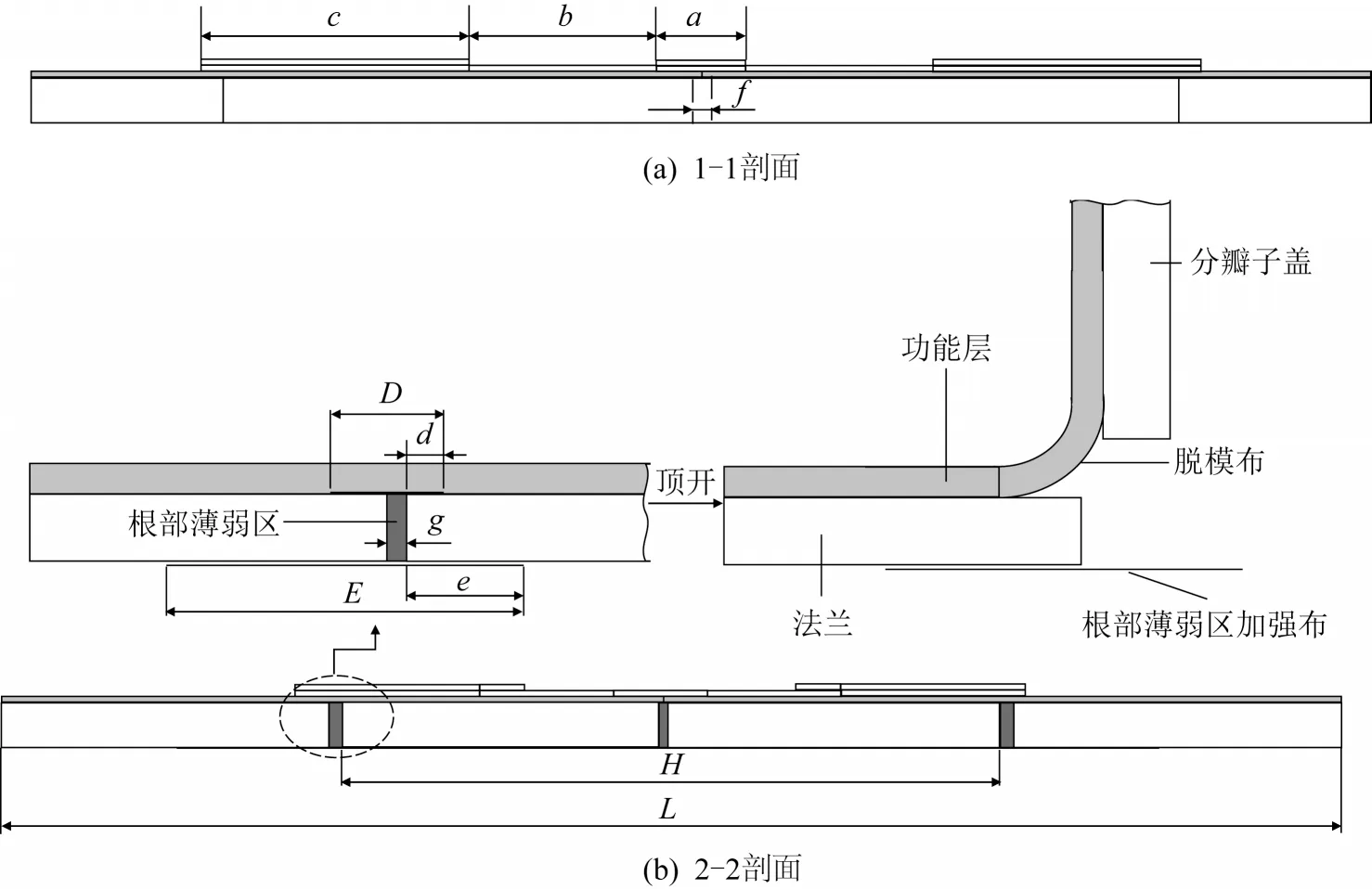
图2 薄弱区处结构示意图Fig.2 Schematic diagram of the structure at the weak area

图3 成型后的易裂盖Fig.3 The fissile cover after molding

表1 易裂盖尺寸Tab.1 Dimensions of the fissile cover

本设计方案在针对具体技术指标时，可通过调整易裂盖的厚度（铺层层数）、功能层的层数、加强布层数和搭接宽度等设计参数，达到预期的性能指标。

2 试验研究

2.1 承压试验

对易裂盖试件进行承压试验，测试其气密性能和最大变形。承压试验所使用的试验装置示意图如图4所示，由模拟发射筒、充气泵、进（出）气管、进（放）气阀和气压表构成。实际安装如图5 所示，易裂盖正面朝上，为模拟真实导弹发射筒内压环境，筒上自带密封条确保气密。易裂盖由压环压实固定，通过螺栓安装在模拟发射筒上。

图4 承压试验装置Fig.4 Pressure test device

图5 易裂盖中心位移测量Fig.5 Center displacement measurement of the fissile cover

试验使用位移传感器测量盖体中心和法兰压环位移，通过盖体中心位移减去压环位移消除误差得到中心真实位移。试验过程中，缓慢向模拟发射筒内加压，通过气压表读取筒内压力，试验从0.016 MPa开始测量，每隔0.002 MPa测一次位移，同时检查气管与阀门处是否漏气，观察易裂盖是否破坏。当气压加到0.038 MPa时，易裂盖漏气。打开放气阀将气体排出，压力回零后，观察易裂盖有无残余变形。图6为易裂盖中心点载荷-位移曲线图，由图可知，随着气压的增加，易裂盖中心的最大变形呈线性变化，气压在0.036 MPa时中心有效最大位移为2.782 5 mm。

图6 易裂盖中心变形Fig.6 Center deformation of the fissile cover

2.2 顶破试验

顶破试验安装如图7所示，先将木质模拟弹头安装在微机万能试验机上，设置弹头向下运动，将易裂盖反面朝上安装，与实际导弹发射时弹头所对一侧一致。随后调整易裂盖所处的支撑架，使弹头与易裂盖中心相对，并固定支撑架。加载速度设置为200 mm/min。

图7 顶破安装图Fig.7 Burst installation diagram

顶破及回弹过程如图8所示。初始时，易裂盖无损伤；弹头与易裂盖接触后，易裂盖中心处薄弱区首先发生破坏；随着弹头的移动，损伤逐渐向分瓣薄弱区扩展；最后，在弹头作用下，根部薄弱区损坏，功能层发生弯曲大变形，易裂盖向四周分四瓣打开。当弹头收回时，分瓣子盖在功能层的作用下按顶破时的破坏路径及时回弹，当弹头完全退出后，分瓣子盖基本复位。

图8 顶破及回弹过程Fig.8 Bursting and rebound process

顶破后易裂盖如图9 所示，4 个分瓣子盖保持完整，薄弱区处加强布与分瓣子盖相连，无碎片掉落。分瓣子盖与法兰无分层破坏，断面处平整，分瓣子盖按预期方式通过功能层与法兰相连，子盖在功能层作用下处于关闭状态。分瓣薄弱区和根部薄弱区的加强布与分瓣子盖之间的破坏模式均为脱粘，试验机所测得顶破力为1.93 kN。

图9 顶破后易裂盖Fig.9 The fissile cover after bursting

3 有限元分析

3.1 承压工况

为研究易裂盖的变形，建立了易裂盖的承压工况有限元分析模型。分瓣子盖、法兰和加强布采用表2中的双向高强玻璃纤维单层板性能参数；薄弱区的胶层采用表3中的AB胶性能参数；模型中在加强布与盖体之间单独建立了一层胶层，以模拟二者之间的胶接，并赋表4中的树脂性能参数。实际工装中，易裂盖通过金属压环和螺栓固定，因此在法兰处使用固支边界条件进行模拟。在易裂盖上施加的载荷为均布载荷。

表2中：、为材料弹性模量；为材料平面剪切模量；为材料泊松比（上述符号下标中的1、2分别代表直角坐标系中x、y方向）。表3中：为AB胶弹性模量；为AB胶泊松比；为AB胶拉伸强度。表4中：为树脂弹性模量；为树脂泊松比；为树脂拉伸强度。

表2 单层板性能参数Tab.2 Properties of the composite laminate

表3 AB胶性能参数Tab.3 Properties of the AB

表4 树脂性能参数Tab.4 Properties of the epoxy resin

图10 为有限元模型在施加0.036 MPa 均布载荷后的应力和变形分布云图。其中，图10（a）为易裂盖整体Mises应力分布云图，图10（b）为易裂盖整体变形分布云图。

图10 易裂盖应力和变形分布Fig.10 Distribution of stress and deformation of the fissile cover

由图10（a）可知，易裂盖整体应力水平较低，最大应力为81.03 MPa。应力相对较高的区域出现在分瓣薄弱区和根部薄弱区，与前文试验中的破坏模式吻合较好。由图10（b）可知，模型变形呈环形分布，中心处变形最大，由中心向根部薄弱区变形逐渐变小。

易裂盖中心点变形试验值与仿真值对比如图11所示，两者变化趋势一致，在0.036 MPa 处有最大误差，为4.08%。因此，本文建立的承压有限元模型较为合理，对易裂盖的变形可有效预测。

图11 试验值与仿真值最大变形对比Fig.11 Comparison of maximum deformation between experimental value and simulated value

3.2 结构参数对变形的影响

基于上述静态承压有限元模型，本文针对易裂盖不同铺层层数、正面与反面加强布层数以及功能层层数对其中心处最大变形的影响进行了分析。在分析易裂盖铺层层数时，保持薄弱区宽度、正反面加强布尺寸、层数与功能层层数等其他参数不变。分别对铺层层数4 层（1.1 mm）、6 层（1.8 mm）、8 层（2.5 mm）、10 层（3.2 mm）、12 层（3.9 mm）、14 层（4.6 mm）、16 层（5.3 mm）、18 层（6.0 mm）、20 层（6.7 mm）、22 层（7.4 mm）这10 种情况下的有限元模型进行了仿真分析。在分析正面加强布影响时，保持盖体铺层层数10层、功能层层数1层，反面加强布尺寸和层数1层不变，分别对正面加强布层数1～5 层的有限元模型进行了仿真分析。在分析反面加强布影响时，保持盖体铺层层数10 层、功能层层数1 层、正面A、B 区加强布层数1 层、C 区加强布2 层不变，分别对反面加强布层数1～5 层的有限元模型进行了仿真分析。在分析功能层层数影响时，保持其余参数不变，分别对功能层层数1～5 层的有限元模型进行了仿真分析。在以上分析中，对盖体均施加0.02 MPa的均布载荷。

图12为易裂盖最大变形随铺层层数的变化曲线，图13为易裂盖最大变形随正面加强布层数的变化曲线，图14为易裂盖最大变形随反面加强布层数的变化曲线，图15为易裂盖最大变形随功能层层数的变化曲线。

图12 最大变形随铺层层数变化曲线Fig.12 The curve of maximum deformation varies with the number of layers

图13 最大变形随正面加强布层数变化曲线Fig.13 The curve of maximum deformation varies with the number of layers in the front reinforcement

图14 最大变形随反面加强布层数变化曲线Fig.14 The curve of maximum deformation varies with the number of layers in the back reinforcement

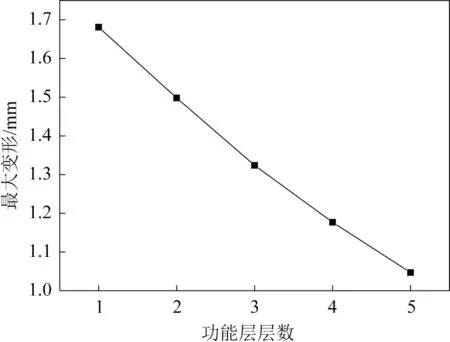
图15 最大变形随功能层层数变化曲线Fig.15 The curve of maximum deformation varies with the number of functional layers

从图12 可以看出，在盖体铺层层数小于12 层时，最大变形随盖体厚度基本呈线性变化，变化显著；当盖体铺层层数从12 层增至16 层时，可以明显看出盖体厚度对最大变形的影响逐渐减弱；当盖体铺层层数从16 层增至22 层时，随厚度增加，最大变形基本不变。从图13～15 可以看出，最大变形随正、反面加强布层数与功能层层数的增加均呈线性递减，且正、反面加强布厚度与功能层层数对最大变形的影响均不显著。正面加强布从1 层增至5 层，最大变形仅减少0.227 mm；反面加强布从1 层增至5 层，最大变形仅减少0.372 mm；功能层层数从1层增至5层，最大变形仅减少0.634 mm。

3.3 顶破工况

为研究易裂盖的顶破性能和损伤机理，本文建立了动态顶破有限元模型。由前文试验研究可知，易裂盖在顶破时，仅有薄弱区AB胶破坏和加强布的脱粘，复合材料盖体并没有发生损伤。因此，在顶破模型中，只对AB胶和加强布胶层进行损伤失效判断。由于AB胶和加强布树脂胶层为各向同性材料，因此使用Von-Mises失效准则对其进行失效判断，其形式如下：

式中：σ、σ、σ、τ、τ、τ为坐标系下应力分量。

顶破工况采用Abaqus显示分析，易裂盖胶层单元设置为破坏后删除单元，弹头约束为刚体，通过施加弹头位移模拟弹头运动。顶破工况下易裂盖应力云图如图16所示。

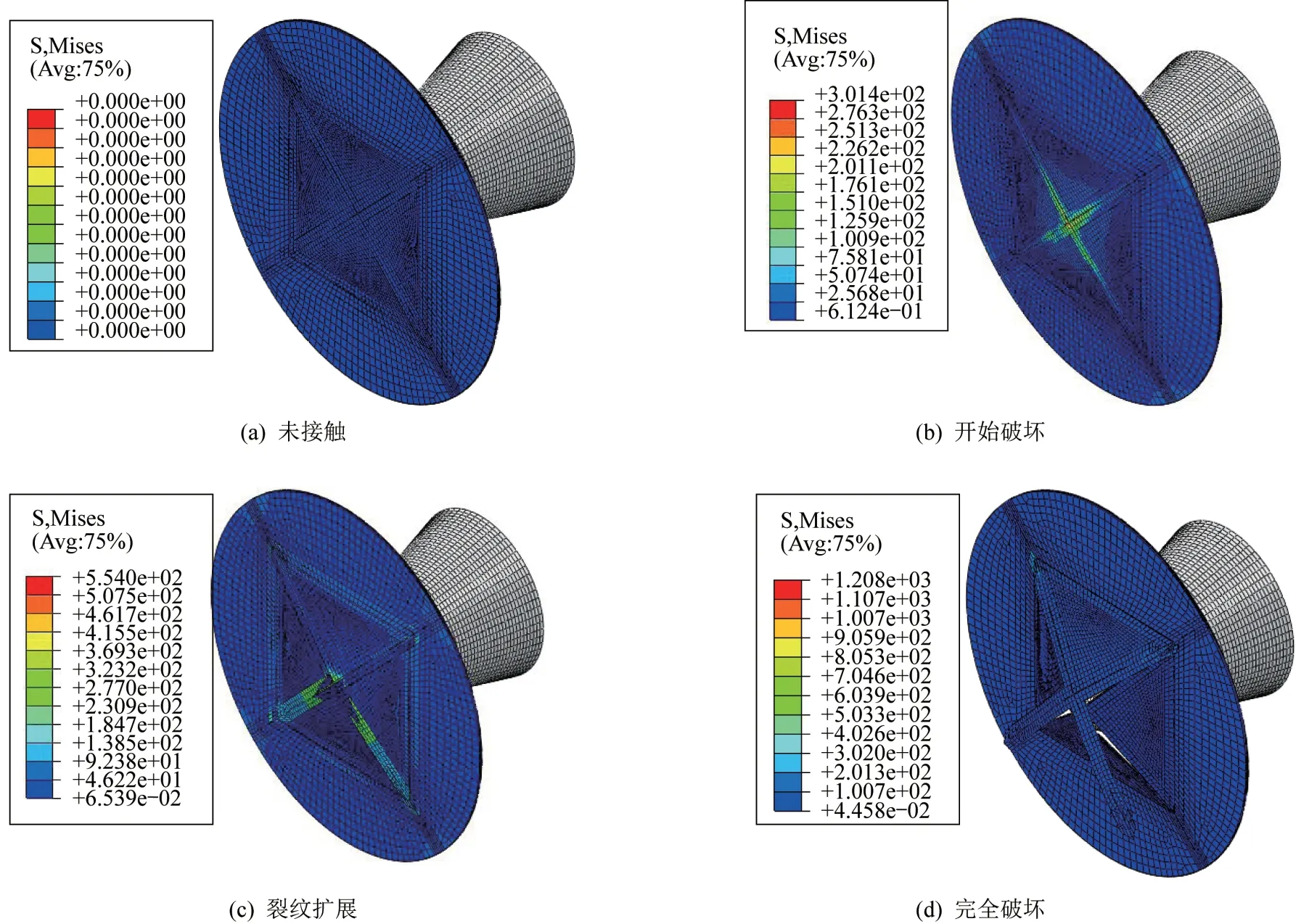
图16 顶破工况下应力云图Fig.16 Stress cloud diagram under bursting conditions

由图16 可知，易裂盖刚开始发生破坏时，易裂盖中心处有应力集中现象，此时分瓣薄弱区AB 胶开始发生损伤破坏，随着弹头继续运动，易裂盖分瓣薄弱区胶层的损伤由中心向根部扩展，并伴随分瓣薄弱区加强布开始脱粘。随后，分瓣薄弱区加强布对分瓣子盖失去粘接作用，盖体开始分瓣，根部薄弱区处加强布由拐角向中心破坏。最后，分瓣子盖之间完全断裂，易裂盖根部薄弱区胶层断裂，分瓣子盖与法兰由功能层连接，功能层发生弯曲大变形，易裂盖分瓣子盖翻折打开。模型破坏形式与试验现象相吻合。有限元计算所得顶破力为2.309 kN，与试验值1.93 kN相差19.64%。综合可知，本文所建顶破有限元模型对顶破效果的模拟较好，对顶破力的预测精度较高。

4 结束语

本文提出了具有回弹复位功能易裂盖的设计方案，并对其进行了承压试验和顶破试验。承压试验结果显示：试制的易裂盖能承受的最大压力为0.036 MPa，在其发生损伤前，中心最大变形随气压载荷的增大呈线性增长趋势。顶破试验结果显示：本文所研究的易裂盖既能按设定的破坏方式破坏，又能在顶破后实现自动回弹复位，所设计的结构满足预期要求。

本文建立了易裂盖相关有限元模型，有限元计算结果与试验结果误差较小，验证了仿真模型的合理性；分析了部分结构参数的变化对承压工况下变形的影响，结果表明，盖体厚度的增大使易裂盖承压工况下最大变形减小，而功能层与正反面加强布层数的增加，对承压工况下盖体最大变形的影响不大。此外，在易裂盖设计中，还可通过调整薄弱区宽度、功能层的层数、分离子盖大小和加强布搭接宽度等设计参数，来达到预期的性能指标。