基于神经网络观测器的无人机编队执行器故障诊断

聂 瑞，王红茹

（哈尔滨工程大学信息与通信工程学院，黑龙江哈尔滨 150000）

0 引 言

无人机是与有人驾驶的飞机具有相同设计理念的航空器，无人机体积小、操作方便，易于在较狭窄的地方执行飞行任务；生产成本较低，在发生故障时更换零件较为方便；更为突出的一点是在辐射较大或有爆炸危险的地域执行任务时，有别于有人驾驶机，地面站人员可直接操纵无人机在指定区域飞行，可避免飞机驾驶员受到伤害。由于这些独特的优点，无人机被广泛应用于国民经济的各个领域，无人机飞行安全问题引起了越来越多的关注。四旋翼无人机具有独立的起降系统，起飞和降落更为方便；所需的起飞面积较小，飞行要求更为简单。对于编队中的单架无人机，无人机的自身结构、执行器、传感器、控制器都会发生各种形式的故障；随着无人机编队中无人机架数的增多，编队中的无人机间发生通信故障的可能性会增加。这些故障都会导致无人机编队飞行任务的失败，因此，对于无人机编队的故障诊断方法进行研究是无人机编队飞行研究的重点。

文献［1］研究了一类非线性多智能体系统的容错控制问题，设计了一种自适应故障估计观测器，用于估计不可测状态值和传感器故障值。文献［2］考虑故障诊断的实时性，设计了追求暂态性能稳定的鲁棒观测器来完成故障诊断，该算法的故障诊断有效准确且具备良好暂态性能。文献［3］从分布式无人机编队各无人机在坐标系下的关系入手，得到无人机编队的外环模型，建立单架无人机非线性动力学方程，建立无人机编队内环模型，在编队发生执行器故障时，设计滑模观测器，对于无人机群编队内无人机之间的通信误差通过有向图进行描述，在观测器中加入相对输出误差，并扩展到全局向量，采用李雅普诺夫稳定法证明了所设计的滑模观测器的稳定性，并在仿真中求解了矩阵的值，完成了对故障的准确估计。

神经网络以其独特的特性被广泛运用于其他方法中，其中较为热门的研究是基于神经网络的状态观测器设计。神经网络是由生物学的神经网络演化而来的成熟的运算方式，神经网络包括若干节点和带有加权值的两节点之间的增益。Polycarpou的团队首先提出了利用神经网络对线性函数和非线性函数的逼近能力设计观测器实现故障诊断，并对观测器的稳定性进行了验证。文献［8］设计了神经网络算法建立观测器，并在卫星姿态控制系统验证了算法的有效性，对于发生的陀螺故障可以有较好的诊断效果。文献［9］将Tough-Set模糊知识与神经网络相结合，利用神经网络逼近非线性函数的能力，对非线性函数形式的故障设计模糊神经网络观测器实现故障估计。文献［10］设计了基于一种自适应神经网络鲁棒观测器的电静液作动器故障诊断方法，在提出一种鲁棒观测器的同时，对液压系统弹性模量产生的不确定性设计参数自适应律进行估计，对于液压系统中的非线性项通过径向基函数（radial basis function，RBF）神经网络予以逼近。

1 径向基函数神经网络技术

神经网络种类众多，主要包括BP 神经网络、径向基神经网络和模糊神经网络等。RBF 神经网络是一种前向传递的神经网络，该神经网络的网络结构含有一个或多个隐藏层，采用径向基函数作为传递函数，能够以任意精度逼近任何非线性函数，其结构如图1所示（图中：=(，，…，x)是RBF神经网络的输入数据；表示隐藏层节点；y表示隐藏层节输出的线性组合）。从结构上看，包括一个输入层、一个隐藏层和一个输出层。输入层的作用是提供外界信号的输入入口，输出层的作用是输出传递函数和加权运算的最终结果，隐藏层提供每个节点都不尽相同的传递函数，不直接与输入/输出发生联系。

图1 RBF网络结构图Fig.1 RBF network structure diagram

每一个输入被赋予一定的权值，与偏差求和后作为神经元传递函数的自变量，其典型传递函数通常是高斯型传递函数，而输出层的结果则是对输入信号的线性组合。定义高斯核函数的表达式为

2 无人机非线性动力学模型与故障描述

无人机的四个旋翼通过十字型的机身连接在一起，由于四个旋翼质量和大小相当，十字型机身的中心即为无人机的重心；四个旋翼距离机身中心的距离相等，高度位于同一水平面。机身上方的旋翼旋转对机身的反作用扭矩会使机身发生旋转，对于无人机机身上安装的摄像头之类的设备不利。为了克服这种情况，设计时要求四个旋翼中左右、前后旋翼旋转方向分别相同，而前旋翼与左旋翼、后旋翼与右旋翼的旋转方向相反。四旋翼无人机结构如图2 所示，图中：、、分别表示四旋翼的角速度，包括俯仰、滚转和偏航角速度；、、、分别表示四旋翼的旋转力矩；、、、分别表示四旋翼的旋转产生的升力。四旋翼无人机三视图及角度描述见图3，无人机姿态运动的3 个欧拉角分别为：俯仰角、翻滚角、偏航角。

图2 四旋翼无人机结构Fig.2 Quadrotor UAV structure

图3 四旋翼无人机三视图及角度表示Fig.3 Quadrotor UAV three-view and angle representation

四旋翼无人机是一个复杂的系统，为了获得四旋翼无人机的准确动力学模型，并方便研究，需要列出以下假设条件：

1）四旋翼无人机是刚体且形状对称。一般地，在建模过程中，忽略地球自转和公转等因素对无人机飞行的影响，并考虑无人机是刚体结构的机身；四旋翼无人机是在低于光速的速度下飞行，不考虑爱因斯坦的狭义相对论中质量发生变化的情况，符合经典物理学定理；地球上的重力加速度不随地域和飞行高度的变化而变化。

例如：在进行《房务实务》这一课程的实践教学过程中，教师在进行讲解的时候就可以请两名学生对前台服务人员的角色进行扮演，然后，教师进行刁钻野蛮的顾客这一角色的扮演，对这两名“服务人员”实施各种的挑剔、甚至要投诉他们。在这一过程中，教师应该引导这两名扮演服务人员的学生将自身的前台服务职能进行充分发挥，对自身的能力加以充分利用，来解决教师在角色扮演中提出的刁钻问题[6]。

2）机体坐标系的原点与四旋翼无人机机体的中心重合。在此假设条件下，根据拉格朗日方法可以最终得到动力学方程为

式中：表示四旋翼无人机的质量：、、分别表示无人机在机体坐标系中沿对应轴的坐标；J、J、J是各姿态角相对应的转动惯量；k表示阻力系数其中=1，2，3，4，5，6；表示重力加速度；表示旋翼的惯性项系数；u、u、u、u表示控制输入，定义四旋翼无人机控制输入与旋翼的角速度相关，则控制输入可表达为

式中：=-+-表示旋翼之间的角速度差；ω，=1，2，3，4表示相对应的四个旋翼的角速度；表示各旋翼计算升力的角速度函数的前缀系数；表示的中心点到机体重心的距离；表示示各旋翼角速度与产生的力矩之间函数关系的前缀系数。

可以得到式（4）所示的形式。

进行故障诊断的研究需要得到无人机的状态空间方程，并且为了方便进行故障诊断观测器的设计，需要将式（4）所示的动力学方程转化为状态空间方程。

式中：=1，2，…，，表示无人机编队中无人机的数量；∈R、∈R、∈R、∈R、∈R是已知的常值矩阵；x()∈R表示编队中第架四旋翼无人机状态变量；u()∈R表示编队中第架四旋翼无人机输入向量；y()∈R表示编队中第架四旋翼无人机可测的输出向量；(x，u，)表示非线性项，取自系统建模过程中的非线性部分。

四旋翼无人机在飞行过程中机体会受到旋翼的气动干扰和各种外来不可抗因素的干扰，从而导致执行器发生故障，因此考虑在建立的四旋翼无人机非线性状态方程中加入执行器故障项和扰动项，在无人机编队系统中单架四旋翼无人机具体的状态方程可表达为

考虑利用RBF 神经网络在线逼近四旋翼无人机的执行器故障，对无人机发生的故障进行实时的故障估计，神经网络对执行器故障的逼近形式可表达为

3 基于神经网络观测器的故障诊断

无人机编队各无人机之间的通信存在误差，这种通信误差如果不及时处理，会一直存在于无人机之间的信息交流过程中，每次新的信息交流又会产生新的误差，误差会超过一定阈值，导致无人机编队实际航行与任务路径大相径庭。因此，设计的观测器必须考虑无人机编队各无人机节点之间的误差信息的传递，本文设计的神经网络观测器中引入相对输出估计误差的概念，其形式为

={，，}用于对于无人机编队系统的编队拓扑结构进行描述。其中：={，，…，υ}在中表示无人机代表的节点所组成的集合；在此基础上⊆×在中表示无人机代表的节点之间连接线的集合；=[a]表示在此拓扑结构下的加权邻接矩阵。对于有向拓扑结构，边集合中的一个元素(υ，υ)∈在中表现为从顶点到顶点的有向线段，理解为无人机可以向无人机传递信息；对于无向拓扑结构，(υ，υ)∈在中表现为从顶点到顶点的无向线段，表示线段两端的节点无人机可以相互交流包括飞行姿态和飞行位置在内的信息。

为了方便研究，在选取加权邻接矩阵=[a]的元素时，一般对加权值的选取非1 即0，加权邻接矩阵可以被简称为邻接矩阵。具体的定义为：在有向拓扑结构中，如果(υ，υ)∈，说明存在第架无人机指向第架无人机的有向线段，邻接矩阵中的元素a=1，若(υ，υ)∈不存在，则a=0；类似地，在无向拓扑结构中，只要(υ，υ)∈成立，那么a=a=1，反之a与a均为0。定义入度矩阵为

对式（17）进行说明：拉普拉斯矩阵=[l]∈R主对角线元素l为邻接矩阵对应行元素的和，主对角线元素为正整数，从而表示在拓扑结构下与无人机相连的节点数目；l的绝对值表示节点与节点连接的情况。拉普拉斯矩阵为=[l]=-。a表示邻接矩阵的元素，l表示拉普拉斯矩阵元素。标定矩阵形式为：=diag(g)∈R，标定矩阵是一个对角矩阵，对角元素表示与长机的连接情况；g表示标定矩阵元素，如果节点与节点0 所代表的长机相连，则g=1，如果没有相连，则g=0，在无人机编队实际飞行中一定存在数量大于等于1的与长机相连的僚机，标定矩阵必定是非零矩阵

要建立全局的误差系统，首先定义单个无人机误差动态方程为

4 仿真验证与结果分析

为验证本文提出的故障诊断算法，以四旋翼无人机姿态控制系统作为诊断对象，其具体参数见表1。

表1 四旋翼无人机系统参数Tab. 1 Quadrotor UAV system parameters

本文采用了1架长机、5架僚机的无人机编队，具体编队结构与无向图描述下的网络拓扑结构如图4所示。

图4 无向图描述下的网络拓扑结构Fig.4 Network topology described by undirected graph

邻接矩阵、入度矩阵、标定矩阵以及拉普拉斯矩阵分别为

考虑执行器故障发生在输入通道，即=。代入四旋翼无人机系统参数表1可得

根据定理，求解不等式，可得

进行仿真时，将此类故障加入到状态方程中。 首先选取外界扰动函数为()=[0.1sin(100) 0.1sin(100)]，然后根据所设计的神经网络观测器中故障的形式，设计三层RBF 神经网络，其中隐藏层网络节点个数为13，各常数选取：=40，=0.05×，=0.000 1。其中表示78行1列全1矩阵，=0.2。

随着飞行次数的增加以及飞行环境的侵蚀，四旋翼无人机会发生各种器件的老化和损坏，导致各种器件不能保证原有的功能特性。四旋翼无人机执行器故障表现为旋翼电机的输出电压存在固定的偏差，定义为突变定值故障。其次，在飞行过程中会受到一些不可抗拒干扰，比如强气流的影响、与漂浮的小体积物体相撞，在这种情况下，四旋翼无人机执行器故障表现为电机的输出电压出现一个不稳定的偏差值，从而引起控制电压连续跳变，定义为缓变故障。

为了测试算法的有效性，设置无人机群故障时应考虑相同时间、不同时间、相同通道、不同通道发生的定值故障和时变故障。仿真时，第架僚机的故障形式表达为

5 架僚机的执行器故障估计仿真结果如图5～9所示。

图5 第1架僚机故障估计Fig.5 Failure estimation of the first UAV

图6 第2架僚机故障估计Fig.6 Failure estimation of the second UAV

图7 第3架僚机故障估计Fig.7 Failure estimation of the third UAV

图8 第4架僚机故障估计Fig.8 Failure estimation of the fourth UAV

图9 第5架僚机故障估计Fig.9 Failure estimation of the fifth UAV

图10 第1架僚机故障估计误差值Fig.10 Error of the first UAV fault estimation

图11 第2架僚机故障估计误差值Fig.11 Error of the second UAV fault estimation

图12 第3架僚机故障估计误差值Fig.12 Error of the third UAV fault estimation

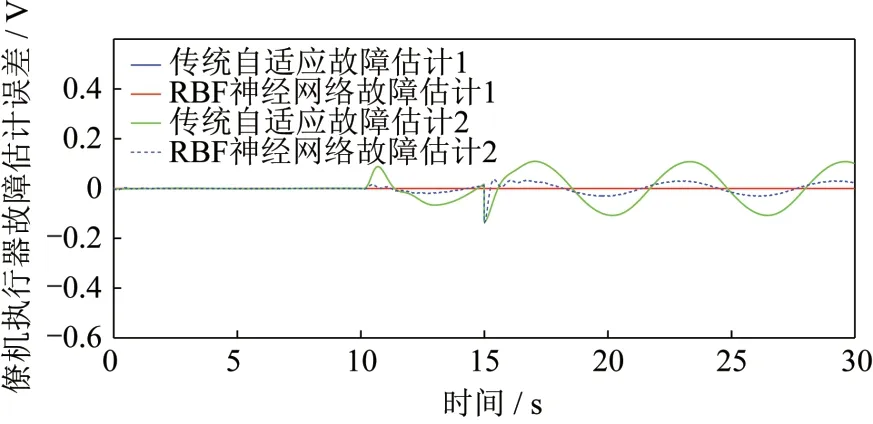
图13 第4架僚机故障估计误差值Fig.13 Error of the fourth UAV fault estimation

图14 第5架僚机故障估计误差值Fig.14 Error of the fifth UAV fault estimation

从图5～9 可以看出，由神经网络对无人机编队中任意一架僚机执行器发生的故障做出的估计都可以很好地拟合真实发生的执行器故障，即真实故障项和故障估计项的曲线拟合效果良好。从图5～7 可以发现，设置多机在同一时间发生执行器故障，对最后无人机编队的故障诊断没有造成影响，在故障发生的起始状态时，故障估计值存在跳变，但在很短的时间内得到及时的纠正，跳变被抑制，故障曲线完成了较好的拟合；由图7～9 可以看到，在不同时间发生的无人机编队中不同僚机上不同通道的执行器故障，神经网络仍然能够较好地拟合故障。从图10～14 可以看出，四旋翼无人机编队中5 架僚机的故障估计误差都很小，可以较好地保持在一定范围，故障估计的效果较为理想。

5 结束语

本文首先建立了四旋翼无人机非线性动力学模型，针对无人机发生执行器故障的情况，加入故障项和外部扰动，设计了神经网络权值和中心值可自主更新的神经网络观测器，从而实现对单个无人机进行故障诊断；然后，引入相对输出估计误差来表征通信误差，构造全局误差系统，从全局角度证明了全局自适应神经网络观测器的稳定性；最后，针对执行器同一通道和不同通道的定值故障和时变故障开展仿真，验证了本文算法可以对故障进行实时估计。