基于动态RCS特征相似的直升机靶机旋翼设计

费钟阳，蒋相闻，招启军

南京航空航天大学 直升机旋翼动力学国家级重点实验室，南京 210016

现代战场上，武装直升机凭借其优良的低空作战能力被广泛使用，成为了战场上具备强有力威胁的目标。能否实现精准打击敌方的武装直升机正逐步成为评价我军防御系统作战能力的重要因素，因此，为了精确评估我军防御系统的作战性能，需要在实战演练环境中构建逼真的直升机靶机系统。雷达散射截面(Radar Cross Section, RCS)是衡量武装直升机隐身性能的重要指标，很大程度上决定了武装直升机的生存力和战斗力，因此对雷达散射特性进行模拟是直升机靶机系统的设计重点之一。

武装直升机种类繁多，它们的RCS特性各不相同。但考虑到工艺和经济因素，不可能对应于每一款潜在威胁直升机目标均设计出一款靶机来模拟它。通常是基于某一小型直升机靶机，通过加载不同规格的龙伯透镜或角反射器等无源干扰设备来增大靶机的整体RCS，达到对于不同直升机目标的雷达散射特性相似性设计效果。但这种构建方案主要是考虑了整机静态的RCS幅值水平，当靶机尺寸较小时，它的旋翼特征与真实直升机目标的旋翼相差较多，旋翼的动态回波信号完全不同，会对雷达识别旋翼类飞行器产生干扰。在飞行过程中不停旋转的旋翼具有独特的动态RCS特性：Pouliguen等开展了旋翼的RCS时频特性分析，获得了常规状态下旋翼雷达回波信号明显的周期性规律；蒙志君等研究了旋翼时域和频域RCS随桨叶片数和转速等因素的变化；陈行勇和蒋相闻等研究了旋翼参数对RCS的影响；Zhou等研究了共轴式旋翼的散射特性；李建周等给出了旋翼转动时直升机雷达回波信号的时频域谱，表明机身的微多普勒频移主要集中于零频附近，而旋翼旋转引起的周期性微多普勒频移较大。因此，为了让靶机模拟出逼近目标直升机的动态RCS特性，需综合考虑不同旋翼时域和频域特征的相似性，但在目前实际的靶机系统构建工作中，对旋翼动态雷达回波信号的提取与分析难度较大，对旋翼的动态散射特征相似性设计的研究也相对较少。

鉴于此，本文首先建立了结合物理光学法和等效电磁流法的RCS高频预估方法，并联合短时傅里叶变换，提取出动态旋翼的雷达回波信号。然后研究了旋翼参数对其动态RCS特性的影响，选取出转速、半径、桨叶片数和翼型厚度作为设计参数，推导得到不同旋翼雷达最大微多普勒频移的相似条件，以时间推进的方式计算了不同翼型配置旋翼的动态RCS，找到使靶机旋翼RCS强度能够与目标旋翼匹配的翼型。最后，综合对比不同设计方案旋翼的时域和频域特征，提出择优方案，完成靶机旋翼到目标旋翼动态RCS的相似性设计。

1 旋翼RCS分析方法

1.1 RCS高频预估方法

在电磁散射求解的问题中，常使用数值分析和高频预估方法，随着研究深入，多种高效高精度混合算法也被提出。但高频预估方法凭借其求解电大尺寸目标问题速度快、精度足以指导工程实践等优点，依然得到广泛应用。本节将联合使用高频预估方法中的物理光学法和等效电磁流法，开展对直升机旋翼雷达特性的计算分析。

1.1.1 物理光学法

物理光学法基于Stratton-Chu积分公式，将散射体等效为散射体表面的感应电流，求解出物体表面外任一观察点的散射电场()为

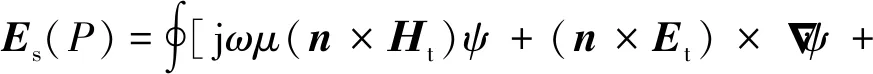
(1)

式中：表示散射体表面积；和分别表示散射体表面处的总电场和总磁场；为磁导率；为散射体表面的单位法矢；为自由空间格林函数；为角频率。

对式(1)的积分方程通过近似条件进行简化，再将目标表面离散成许多曲面微元，把微元的散射场积分叠加即可得到目标表面在远处任一观察点的散射电场：

(2)

式中：为波数；为目标到雷达天线的距离；为坐标轴矢量；为入射电场。这样通过曲面积分叠加，即可求出整个目标表面的散射场。

1.1.2 等效电磁流法

物理光学法未能考虑边缘绕射，需要引入等效电磁流法进行修正。等效电磁流法假设在目标表面奇异处(如尖劈)的边缘回路存在线电流和线磁流，对其进行远场辐射积分求得绕射场：

(3)

式中：d为边缘微元回路；为波阻抗；为绕射射线传播方向的单位法矢；为沿边缘回路方向的单位矢量；为边缘的位置法矢。

从绕射场公式中剔除物理光学场的贡献，可以求得后向散射绕射场为

(4)

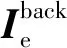
1.1.3 旋翼总散射场的计算

通过物理光学法计算旋翼面元散射场()，等效电磁流法计算旋翼边缘绕射场，将二者矢量叠加可求得旋翼的总散射电场：

=()+

(5)

1.1.4 算例验证

为了验证本节建立的旋翼RCS高频近似求解方法的有效性，选用有RCS参考值的NACA0012翼型平直桨叶作为算例。计算条件为：雷达波频率5 GHz，垂直极化。从图1可以看出计算值和参考值吻合度较高，说明此高频方法能有效模拟复杂外形目标的RCS，可以用于旋翼雷达目标特性的计算和分析。

图1 RCS本文计算值与参考值[25]对比Fig.1 RCS comparisons of present results with reference results[25]

1.2 RCS时频分析方法

时频分析方法基于短时傅里叶变换，将连续时间离散后在不同的时间点对高频预估方法计算得到的回波信号作傅里叶变换得到瞬态频域分布，再依靠时间窗的滑动得到二维的时间-频率密度分布，表征出动态旋翼的RCS时频特性。本文选用Hamming窗开展旋翼RCS的时频信号提取。针对有时频信号测试结果的旋翼，半径0.49 m，包含2片桨叶，在10 GHz、水平极化雷达波照射下，时频信号曲线的测试结果和计算结果如图2所示。可以看出计算结果与试验测试结果基本吻合(雷达最大微多普勒频移大小及出现的时间相同)，验证了本文建立的旋翼雷达回波信号时频分析方法的有效性。

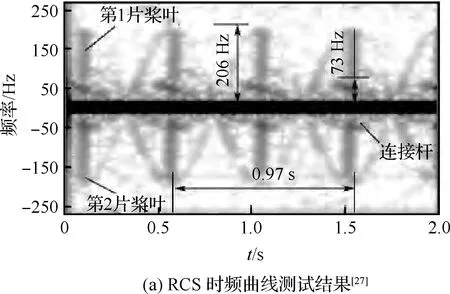
图2 本文与文献[27]RCS时频曲线结果对比Fig.2 Comparison of RCS time-frequency curves of present result with those of Ref.[27] result

2 旋翼参数对RCS时频特性的影响

旋翼RCS的时频域谱揭示了在各个时刻不同频率的旋翼雷达回波信号的能量密度分布。时频域谱中的微多普勒特征包含了旋翼的转速、半径和桨叶片数等信息，灰度的亮暗则与旋翼的动态RCS强度有关，这由旋翼的散射特性决定，因此，时频域谱能够充分反映旋翼旋转过程的动态RCS特性。为此，本节将基于表1中的4副旋翼，开展靶机旋翼参数对RCS时频特性的影响研究。

表1 不同参数的旋翼Table 1 Rotors with different parameters

2.1 旋翼RCS时频域谱特征

由旋翼旋转引起雷达最大多普勒频移为

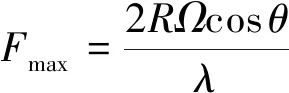
(6)

式中：为旋翼半径；为旋翼转速;为雷达波入射方向与桨盘平面夹角；为波长。

图3展示了旋翼1在雷达波频率为10 GHz、垂直极化条件下，一个旋转周期内的RCS时频域谱，它的雷达最大微多普勒频移为4 188.79 Hz。

图3中白色实线线框表示的是雷达最大微多普勒频移闪烁带(“雷达最大微多普勒频移闪烁带”在后文中均简称为“闪烁带”)，闪烁带对应的横轴频率即为雷达最大微多普勒频移，当桨叶前缘或后缘旋转至垂直于雷达波的入射方向时会产生较强的散射回波(如图4所示)，时频域谱上出现闪烁带，迎着雷达波运动的桨叶产生正频率的闪烁带，背对雷达波运动的桨叶产生负频率的闪烁带；图3中黄色虚线框内标识了某些闪烁点的位置，这些闪烁点是当雷达波垂直照射到桨尖端面时产生的强散射源表征，主要集中于零频附近。

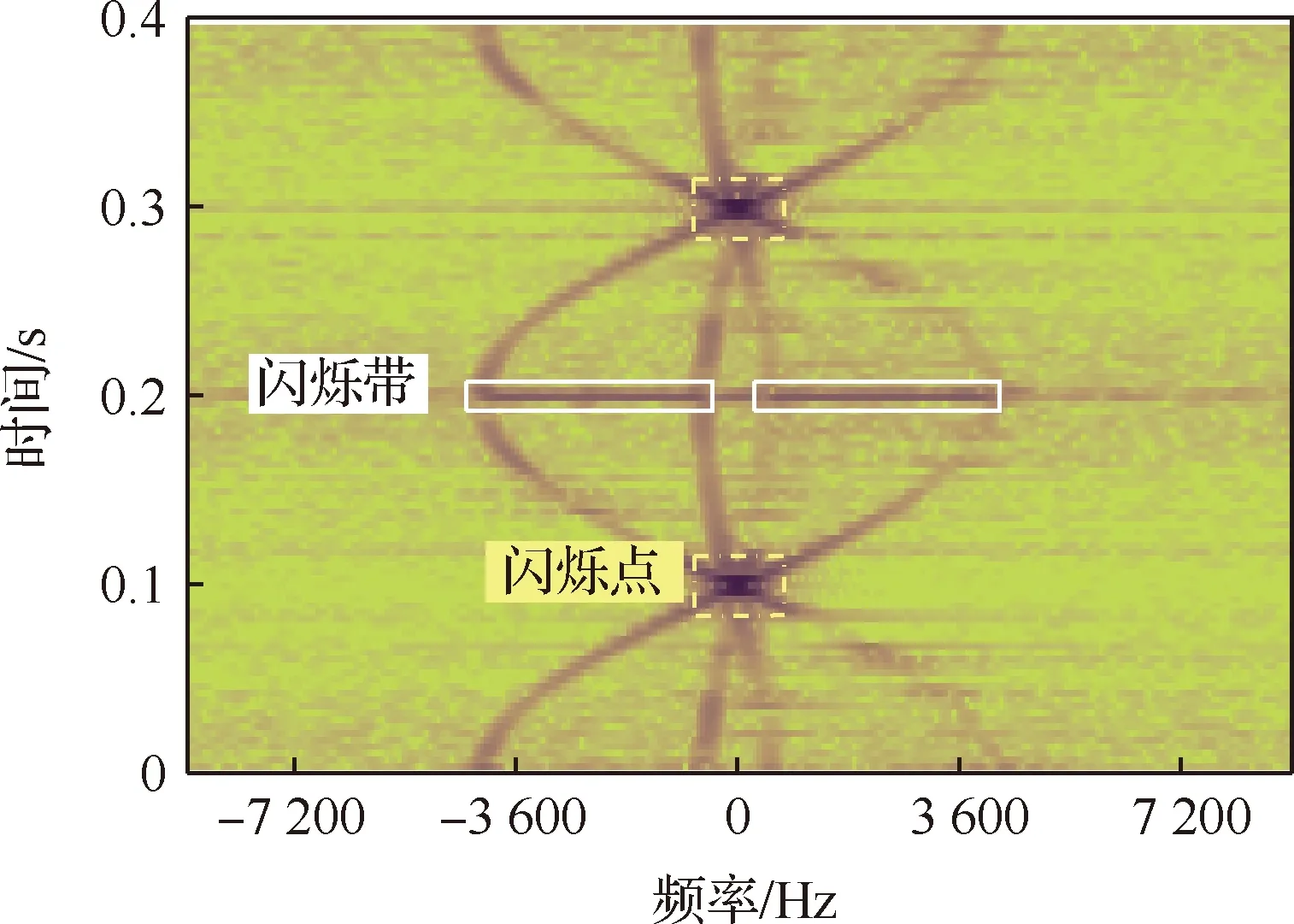
图3 旋翼1的时频域谱Fig.3 Time-frequency spectrum of Rotor 1

图4 闪烁带与闪烁点成因Fig.4 Causes of scintillation bands and scintillation points

2.2 旋翼基本参数的影响

2.2.1 浆叶片数

为了研究桨叶片数对雷达最大微多普勒频移的影响，通过时频分析方法得到旋翼2在10 GHz、垂直极化雷达波照射下的RCS时频域谱,如图5所示。由图可以看到，旋翼2的雷达最大微多普勒频移=4 188.79 Hz，与旋翼1一致，但在一个旋转周期0.4 s内产生了4次闪烁带。当只有旋翼桨叶片数发生改变时，桨叶的分布会变得稀疏或紧密，会导致相同时间内出现闪烁带的次数发生变化，桨叶片数增加则闪烁带次数增加。

为了研究桨叶片数对旋翼RCS强度的影响，基于转速和半径相同的3副平直桨叶旋翼，桨叶片数分别为2、4和6片，在相同条件下计算它们在水平面内的RCS分布，如图6所示。旋翼的RCS幅值在水平面的大部分角域都维持在较低水平，当雷达波垂直入射到桨叶前缘(即2片桨叶旋翼的×180°方位、4片桨叶旋翼的×90°方位、6片桨叶旋翼的×60°方位，=0,1,2,…)时将产生强烈的散射回波，这些方位角附近会存在RCS极大值，当桨叶为偶数片时，水平面内RCS极大值的个数等于旋翼桨叶片数。

图5 旋翼2的时频域谱Fig.5 Time-frequency spectrum of Rotor 2

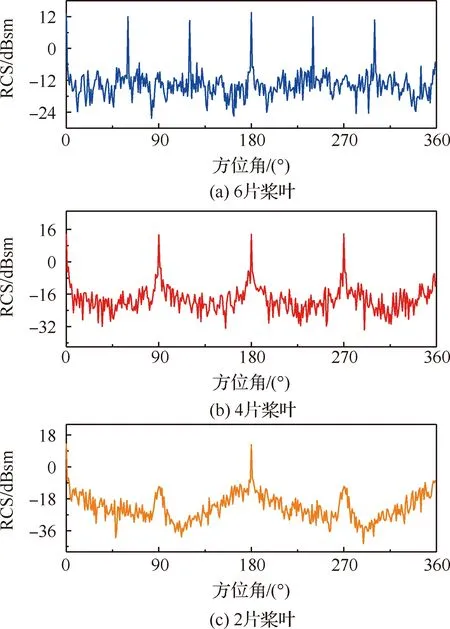
图6 不同桨叶片数旋翼RCS分布对比Fig.6 Comparison of RCS distribution of rotors with different blade numbers

2.2.2 旋翼半径

为了研究旋翼半径对雷达最大微多普勒频移的影响，在相同计算条件下得到旋翼4在一个旋转周期内的时频域谱(见图7)：旋翼4的雷达最大微多普勒频移=2 094.40 Hz，出现了2次闪烁带。当只有旋翼半径改变时，仅会导致雷达最大微多普勒频移发生变化，半径越小，频移越小。

图7 旋翼4的时频曲线Fig.7 Time-frequency spectrum of Rotor 4

为了研究旋翼半径对RCS强度的影响，在相同条件下，计算3副半径不同的2片桨叶旋翼的水平面RCS均值，从图8可以看出，随着旋翼半径的减小，桨叶前缘镜面散射被削弱，RCS均值逐渐降低。

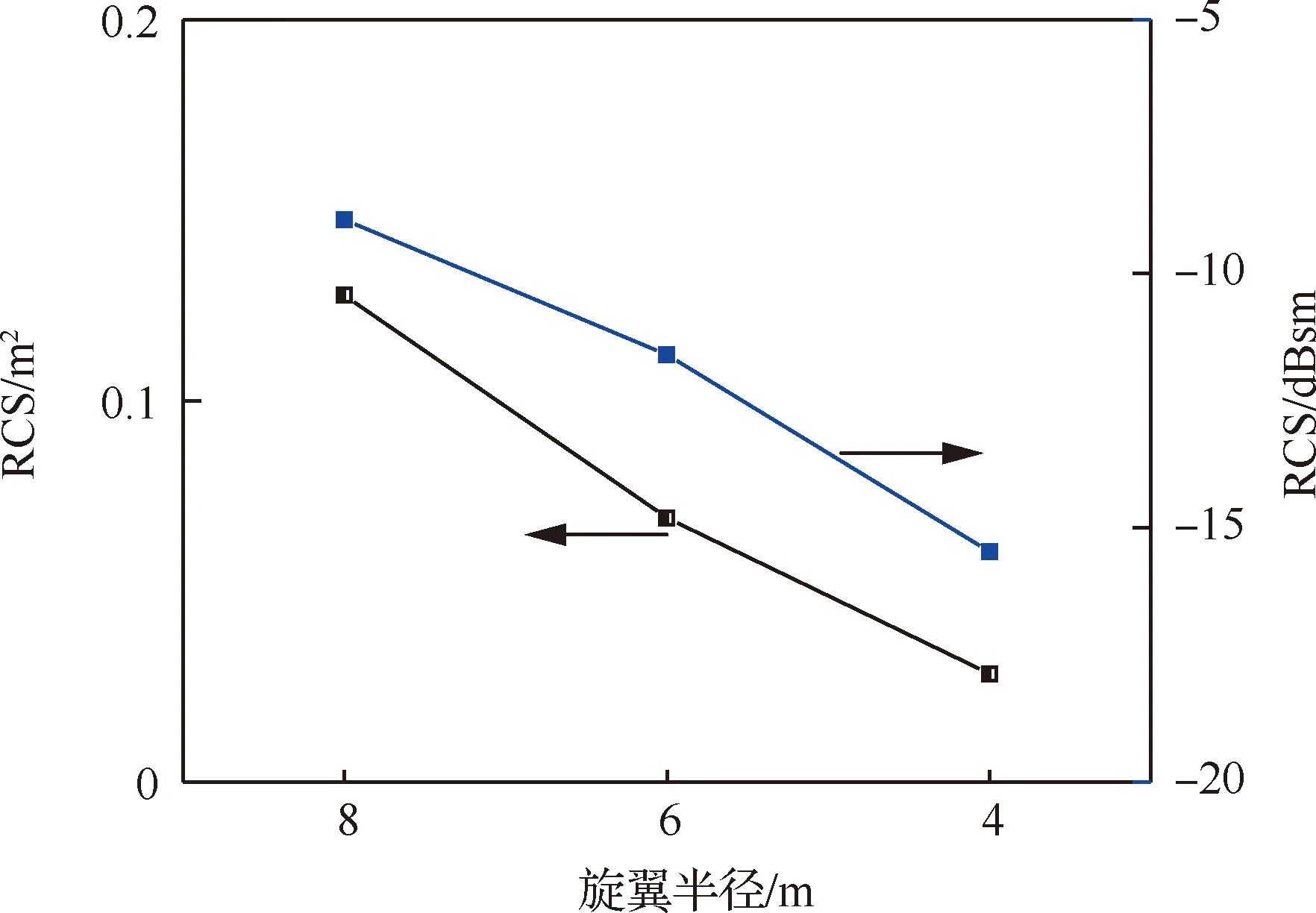
图8 不同半径旋翼RCS均值对比Fig.8 Comparison of RCS mean values of rotors with different radius

2.3 旋翼翼型参数的影响

图9分别给出了旋翼1采用NACA0012、NACA0014、NACA0016、NACA0018和NACA0020这5种不同厚度翼型以及NACA1412、NACA2412、NACA3412、NACA4412和NACA5412这5种不同最大弯度翼型的RCS均值对比。可以看出：随着翼型厚度的增加，旋翼1的RCS均值不断增大；翼型弯度的增加会使RCS均值在小范围内上下波动，但变化幅度远小于翼型厚度改变带来的影响。因此，相比于翼型弯度，翼型厚度的改变更能主导旋翼RCS的变化，对靶机旋翼翼型厚度的设计是RCS强度相似性设计中重要的一环。

由于旋翼的微多普勒特征主要由旋翼的基本参数和雷达波入射角度决定，翼型的不同只对RCS强度产生较明显的影响。因此，进行雷达最大微多普勒频移相似性设计时不考虑翼型的影响。

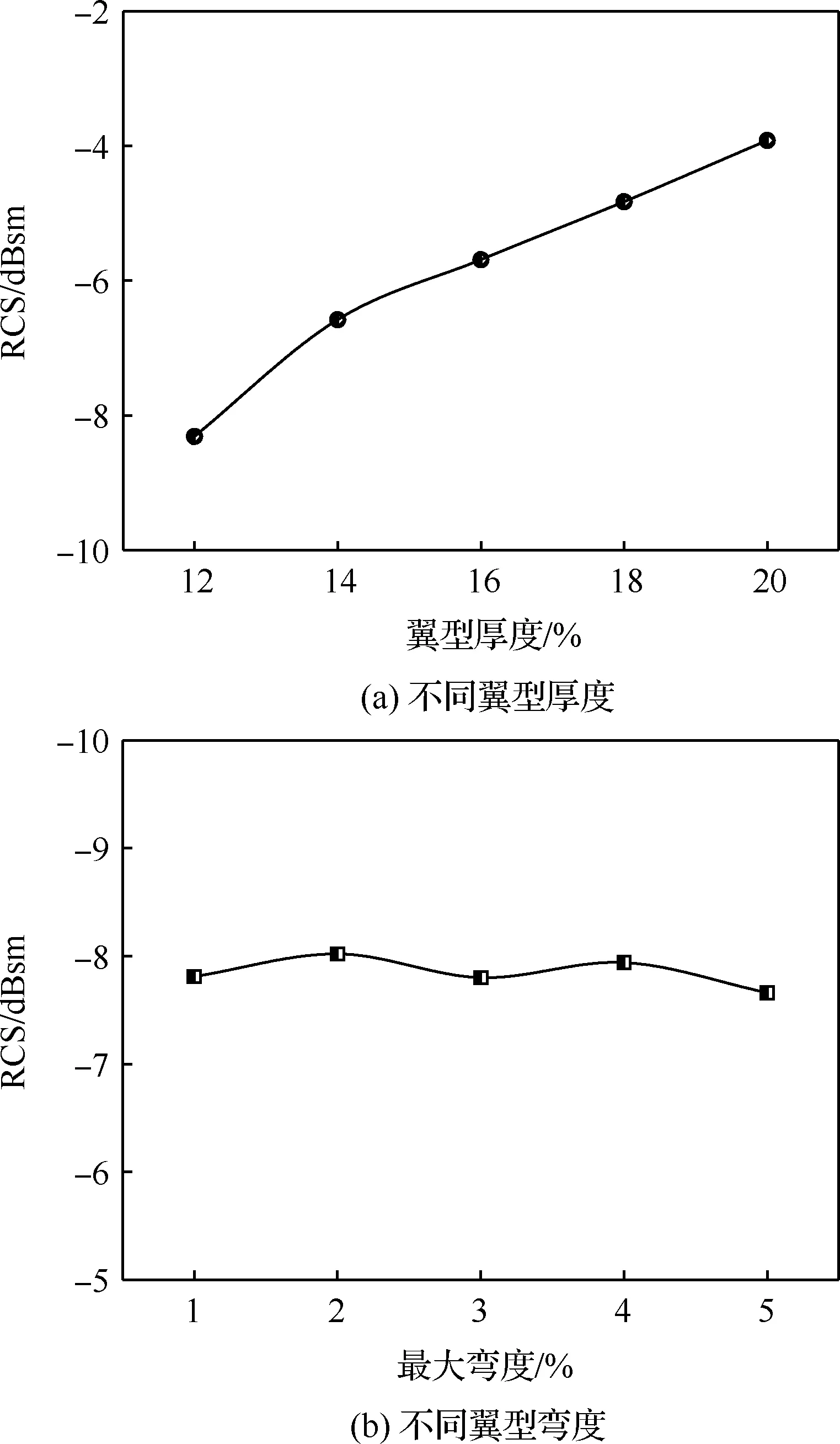
图9 翼型参数对旋翼1的RCS特性影响Fig.9 Effect of airfoil parameters on RCS characteristics of Rotor 1

2.4 旋翼运动参数的影响

2.4.1 旋翼转速

为了研究旋翼转速对雷达最大微多普勒频移的影响，计算得到旋翼3在0.4 s内的时频域谱(见图10)：旋翼3的雷达最大微多普勒频移=8 377.58 Hz，出现了4次闪烁带。

根据式(6)，雷达最大微多普勒频移与转速成正相关，当只有旋翼转速改变时，雷达最大微多普勒频移会发生变化；同时，旋翼转速变化会改变桨叶前、后缘在相同时间内垂直于雷达波入射方向的机会，转速越快，相同时间内出现闪烁带的次数越多。

为了研究旋翼转速对RCS强度的影响，在相同条件下，计算同一副2片桨叶旋翼在1、2和3(表示某转速数值)这3个转速时的时域RCS，如图11所示。雷达照射持续时间为(转速为1旋翼的旋转周期)，RCS采样间隔时间为/360。可以看出，由于旋翼转速的提高，在相同时间内某片桨叶前缘垂直于入射波的状态增加，因此RCS极大值区域依次出现的时间间隔变短，相同时间内转速越高的旋翼时域RCS极大值区域越多。

图10 旋翼3的时频域谱Fig.10 Time-frequency spectrum of Rotor 3

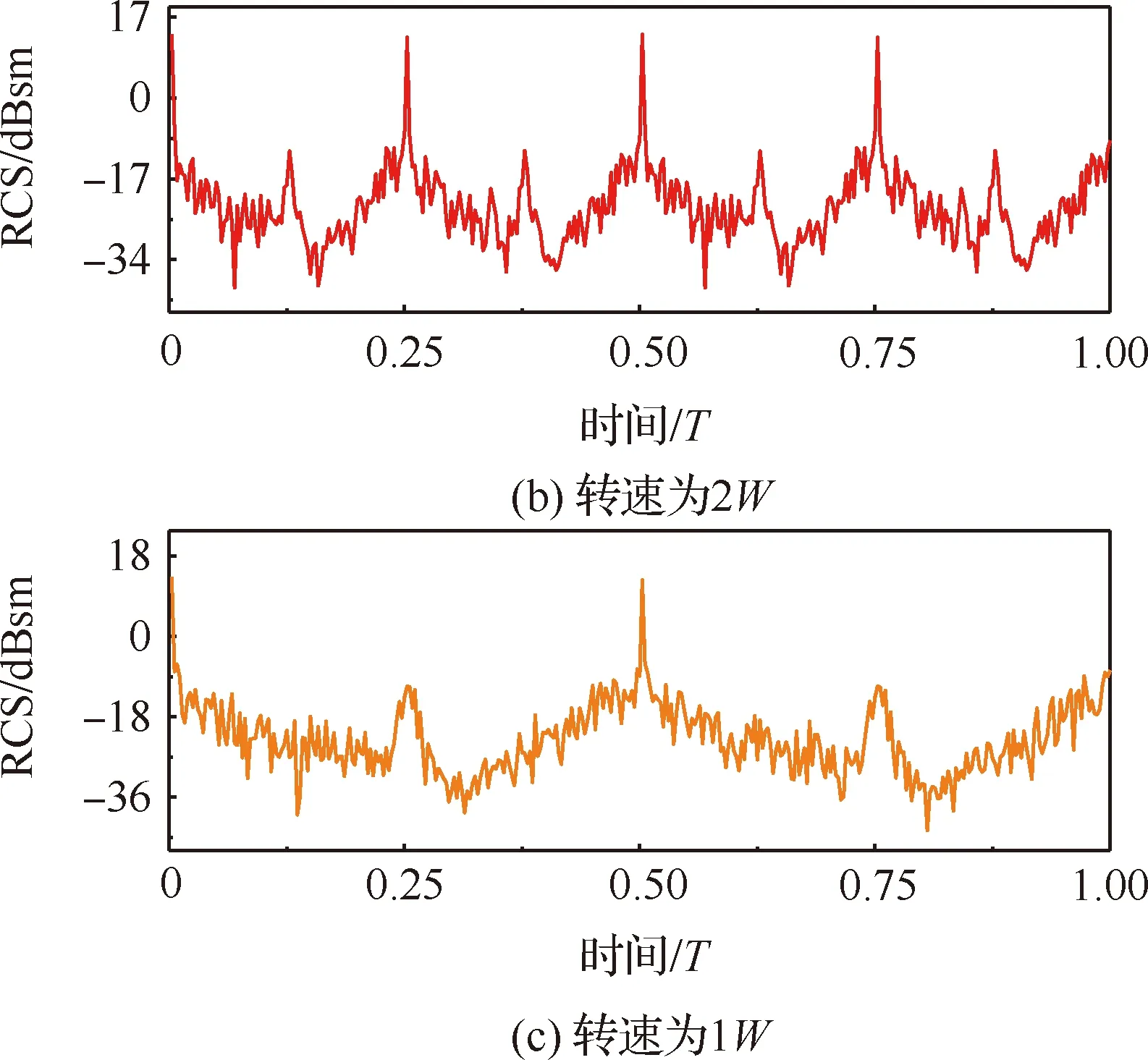
图11 不同转速旋翼时域RCS分布对比Fig.11 Comparison of RCS distribution in time domain of rotors at different rotational speed

2.4.2 桨叶挥舞运动

挥舞运动是旋翼动态运动中重要的组成部分，本节将研究挥舞运动对旋翼动态散射特性的影响。

桨叶的挥舞角主要由锥度角、后倒角和侧倒角共同决定，通常情况下这3个角度分量均比较小。图12给出了旋翼1在不同的锥度角、后倒角和侧倒角状态下的RCS均值对比。可以看出，侧倒角从3°变到6°再至9°，RCS均值几乎不变，锥度角和后倒角的增加使RCS的均值呈下降趋势，但引起的变化量在-18 dB以内。因此，相较于其他的旋翼参数，挥舞角分量对RCS强度的影响较小。

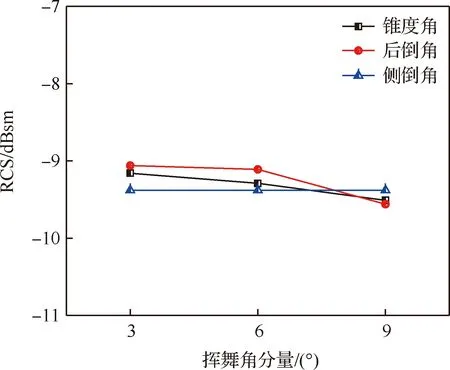
图12 挥舞角分量对RCS均值的影响Fig.12 Effect of flap angle components on RCS mean value

图13是锥度角、后倒角和侧倒角均分别为9°时的RCS时频域谱，雷达波从旋翼头向入射。从图中可以看出3种情况下的雷达最大微多普勒频率基本一致，但存在细微差别，具体的频率数值为：锥度角或后倒角为9°时=4 13722 Hz，侧倒角为9°时=4 18879 Hz，频率差在1%左右。这是由于挥舞角分量在多数情况下较小，只能对雷达波至旋翼的入射方向产生较弱的影响。

以上研究了挥舞角分量对旋翼散射特性的影响，再分别计算在头向固定方位的雷达波照射下，旋翼1以3种挥舞角分布状态旋转一周的动态RCS，得到它们的RCS均值如表2所示,其中为桨叶方位角。

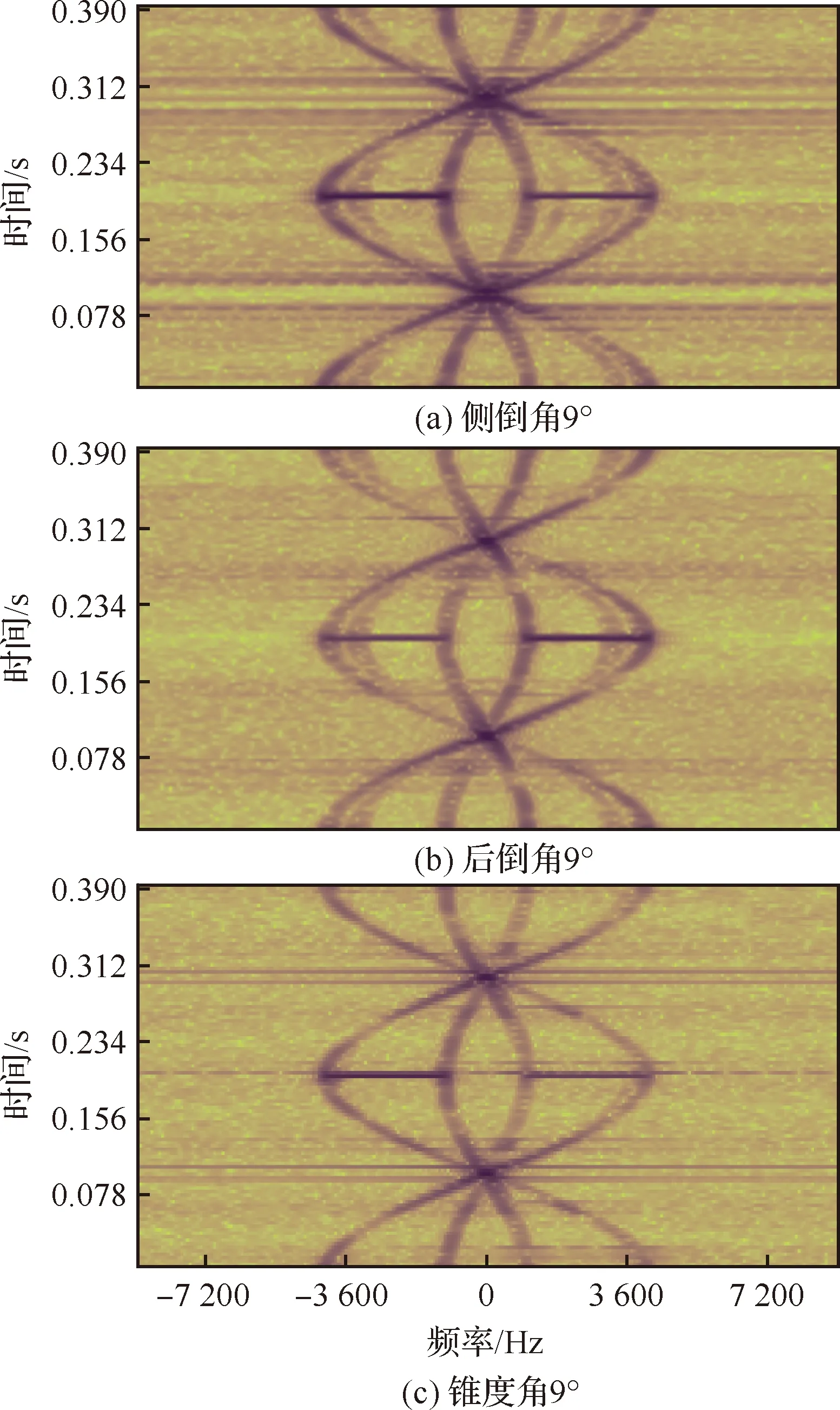
图13 挥舞角分量对RCS时频域谱的影响Fig.13 Effect of flap angle components on RCS time-frequency domain spectrum

表2 不同挥舞角旋翼的RCS均值对比

由表2可以看出，旋翼在具有挥舞角的状态下，挥舞角变化引起的RCS均值变化幅度较小。并且在实际飞行中，桨叶的挥舞角与当地气动环境以及飞行状态相关，目标旋翼和靶机旋翼各自的挥舞角难以被实时跟踪。因此，旋翼的挥舞角及其分量不作为本文相似性设计的参数之一。

3 靶机旋翼动态RCS相似性设计

3.1 雷达最大微多普勒频移相似性设计

雷达最大微多普勒频移作为旋翼RCS时频域谱中最重要的特征，是雷达对靶机旋翼进行识别的主要依据。

分析：对比两位译者的译文可以发现，译者男女性别身份的不同，对惊叹语的表达方式也是不一样的。文中旨在探讨为什么詹金斯一家每日入不敷出，却仍过得十分潇洒，其中就提到是不是因为詹金斯的老婆是有钱人家，那么文中用了一个惊叹语“Pooh”旨在表现出詹金斯的老婆根本没钱，加强语气。因此，对比杨译的“呸”与荣译的“瞎掰”，可以看出，荣译发挥了自己男性地位要高于女性的特征，男性更倾向于说一些语气强硬的惊叹语，而女性，如杨译的“呸”，就显得略弱些。

第2节研究了旋翼参数对RCS特性的影响，其中，桨叶片数、转速和半径3个基本参数中任意一个发生变化，雷达最大微多普勒频移特征都会发生显著改变。与此同时，由于直升机靶机型号有限，旋翼半径大体上被限制在某一范围内，所以与半径差别较大的目标旋翼相比，雷达最大微多普勒频移通常差别较大。若能实现半径不同的旋翼之间的雷达最大微多普勒频移相似，则直升机靶机模拟不同目标RCS的真实性和适用性将得到提升。本节将开展靶机旋翼雷达最大微多普勒频移特征相似性设计研究。

假设目标旋翼有片桨叶，转速为，半径为；靶机旋翼对应的是桨叶片数，转速和半径。根据式(6)，两副旋翼的雷达最大多普勒频移、分别为

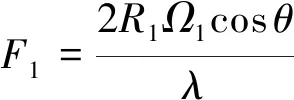
(7)

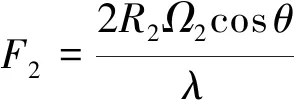
(8)

雷达波入射角和波长不变，要使旋翼的最大微多普勒频移相同，即=成立，只需要=，即

(9)

式(9)对靶机旋翼与目标旋翼的半径和转速间的关系作了规定。当两副旋翼的半径不同、转速不同时，若它们的桨叶片数相同，那么在相同时间内闪烁带出现的次数不同，因此需要对桨叶片数做出调整。秒内，目标旋翼和靶机旋翼出现的正(负)闪烁带次数、分别为

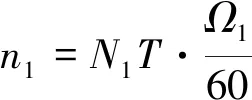
(10)

(11)

要使=，两副旋翼需要满足条件=，即

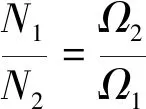
(12)

综合式(9)、式(12)，若要使半径、转速和桨叶片数均不同的靶机旋翼与目标旋翼雷达最大微多普勒频移具有相似性，满足如下相似性条件即可：

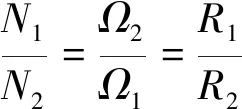
(13)

同时，偶数片桨叶旋翼在结构上具有对称性，总会出现一片桨叶前缘垂直于入射波的同时另一片桨叶的后缘垂直于入射波，因此正、负闪烁带总是同时出现；而奇数片桨叶旋翼在结构上非对称，正、负闪烁带交替出现。桨叶片数的奇偶性决定了旋翼时频域谱中的闪烁带是否对称，所以进行雷达最大微多普勒频移相似性设计还要加上一个前提条件：靶机旋翼与目标旋翼的桨叶片数奇偶性需保持一致。

为了验证上述推导的雷达最大微多普勒频移相似性条件的可行性，并考虑到常规旋翼通常有2～8片桨叶，建立如表3所示的一组偶数片桨叶的不同旋翼模型，计算出它们在垂直极化、10 GHz雷达波照射下的时频域谱。

从图14中可以看到4副旋翼的时频域谱中雷达最大微多普勒频移特征基本一致：雷达最大微多普勒频移均为8 377.58 Hz；每两次正闪烁带或负闪烁带出现的时间间隔相同，均为0.05 s，在同一时间内出现相同次数的闪烁带。

为了验证本节方法能否应用于奇数片桨叶旋翼的设计，建立如表4所示的两副旋翼模型，并提取它们在0～0.4 s内的雷达回波信号得到时频域谱，如图15所示。

表3 偶数片桨叶旋翼参数Table 3 Parameters of rotors with even blades

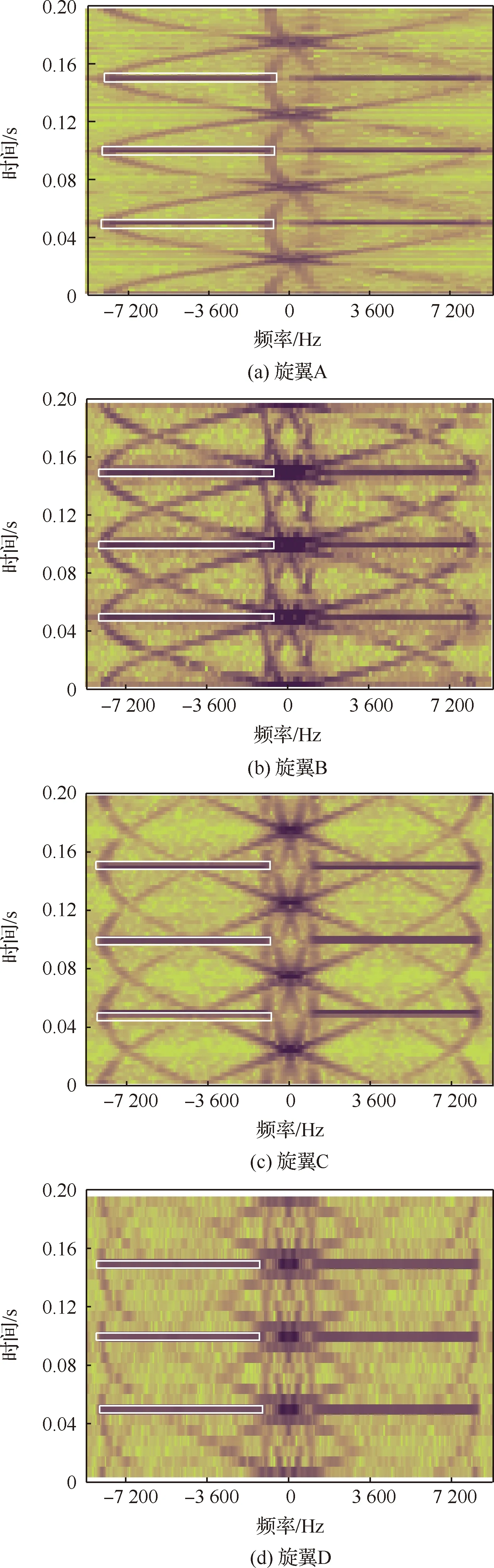
图14 偶数片桨叶旋翼时频域谱Fig.14 Time-frequency spectrums of rotors with even blades

从图15中可以看到，两副旋翼的雷达最大微多普勒频移带宽相同，且两次闪烁带出现的时间间隔一致，验证了相似性条件同样适用于靶机旋翼对奇数片桨叶目标旋翼的雷达最大微多普勒频移特征相似性设计。上述结果表明了通过已知的目标旋翼基本参数，基于本节给定的相似性条件构造靶机旋翼，能够使它们具备相似的雷达最大微多普勒频移特征。

表4 奇数片桨叶旋翼参数Table 4 Parameters of rotors with odd blades

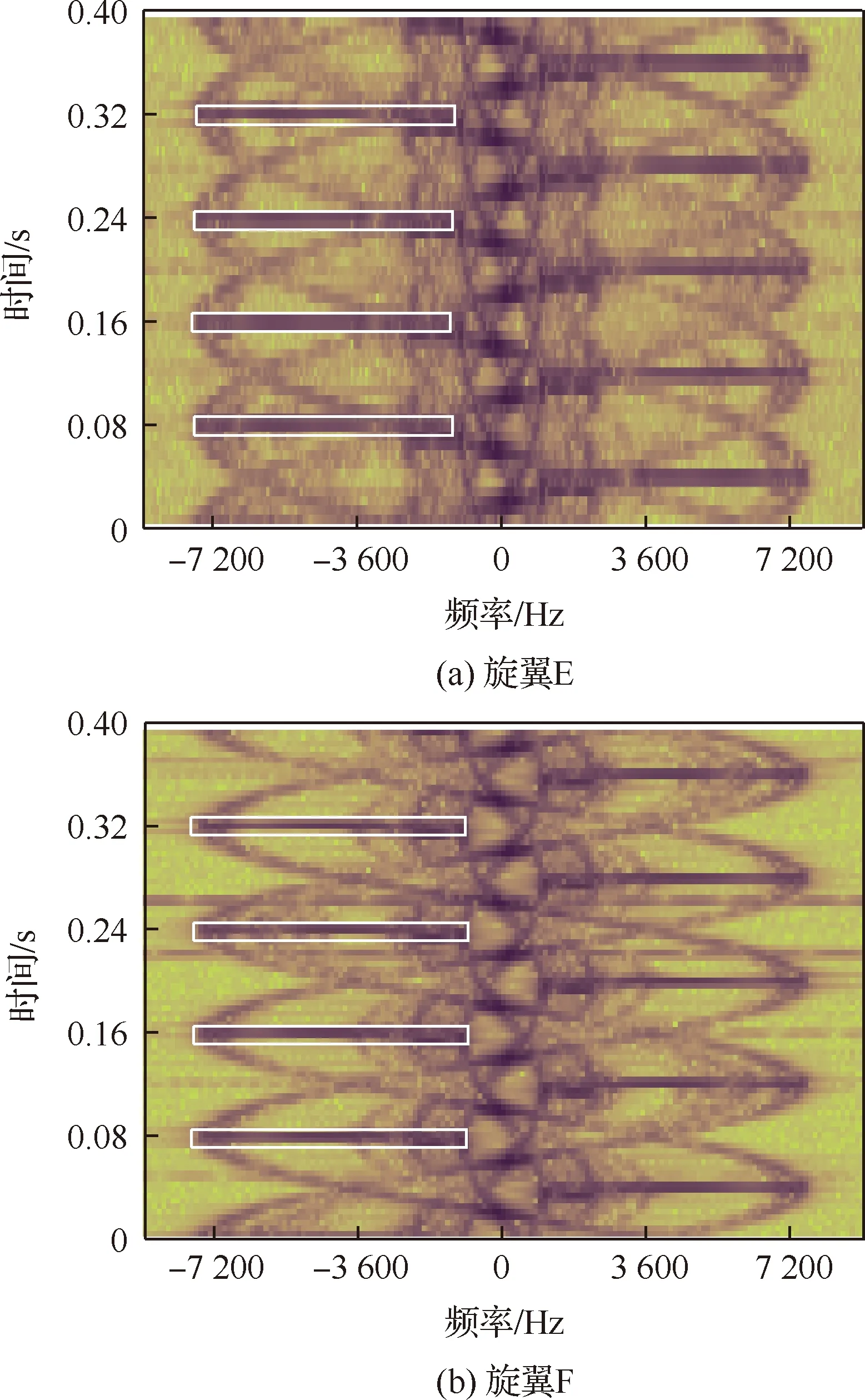
图15 奇数片桨叶旋翼时频域谱Fig.15 Time-frequency spectrums of rotors with odd blades

3.2 RCS强度相似性设计

3.1节研究了通过调整桨叶片数、转速和半径等基本参数，能够进行靶机旋翼的最大微多普勒频移特征相似性的设计，同时旋翼的动态RCS时频域谱中还展现了另一种重要的特征，即旋翼动态RCS强度。RCS强度由时频域谱的灰度亮暗程度和分布共同体现。

在进行雷达最大微多普勒频移相似性设计时，靶机旋翼与目标旋翼的桨叶片数、转速和半径区别较大，而上述3个参数的任意一个发生变化都会造成旋翼RCS强度在时域上的特征差距明显，进而导致时频域谱亮暗分布不同。鉴于此，本节将在靶机旋翼已经完成雷达最大微多普勒频移相似性设计的基础上，开展如何进一步完成动态RCS强度的相似性设计研究。

选取表3中旋翼B、C、D(3副旋翼的雷达最大微多普勒频移特征一致)，假设3副旋翼采用相同弦长的NACA0010翼型，在10 GHz、垂直极化雷达波条件下计算它们的水平面RCS均值：旋翼D为-3.598 dBsm，旋翼C为-5.759 dBsm，旋翼B为-8.539 dBsm，可以明显看到随着桨叶片数和半径的减小，RCS强度逐渐降低。

在弦长一定的条件下，采用相对厚度小的翼型能够降低RCS的强度。以旋翼D作为目标旋翼，采用NACA0010翼型；选择旋翼C和旋翼B作为靶机旋翼类型，控制旋翼实度不变，都分别采用NACA0010、NACA0012、NACA0014、NACA0016、NACA0018和NACA0020这6种翼型。得到它们在水平面的RCS均值随翼型变化如图16 所示。

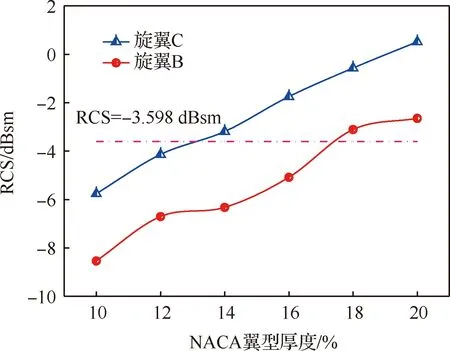
图16 RCS均值随翼型厚度变化规律(偶数片)Fig.16 Mean RCS varying with airfoil thickness (even blades)

图16中横线代表的是目标旋翼D的RCS均值(-3.598 dBsm)。不同的旋翼RCS均值都随着翼型厚度的增加而增加，在相同翼型厚度下旋翼C的RCS大于旋翼B。当3副旋翼均采用NACA0010翼型时，目标旋翼D的RCS大于旋翼C和旋翼B，随着翼型厚度的增加，旋翼C和B的RCS逐渐超过目标旋翼。总体来看，目标旋翼D的RCS与采用NACA0014翼型的旋翼C和采用NACA0018翼型的旋翼B最为接近，二者分别是-3.190 dBsm和-3.109 dBsm。以上是对旋翼的RCS均值进行分析，为了研究旋翼动态RCS在时域上的分布状况，规定收发雷达位置和旋翼中心位置不变(见图17)，采用时间推进的方式对这3副旋翼在不同时间点的RCS进行采样。旋翼D、C、B的旋转周期分别为0.4 s、0.3 s和0.2 s，在相同计算条件下得到它们以各自转速旋转0～0.4 s的RCS分布，如图18所示。

从图18可以看出目标旋翼与靶机旋翼在相同时刻出现RCS极大值区域，幅值较为接近，RCS随时间的分布规律基本一致。表明了对于雷达最大微多普勒频移特征相似，但基本参数完全不同的靶机旋翼与目标旋翼，能够通过改变翼型厚度使它们进一步具有相似的RCS均值和时域RCS动态分布，达到靶机旋翼动态RCS强度相似性设计的目标。

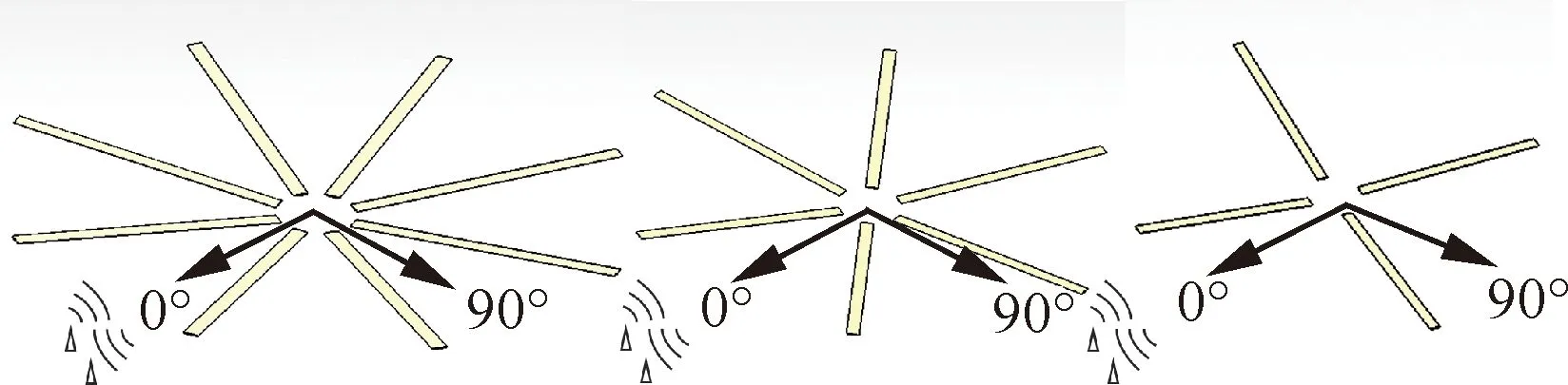
图17 收发雷达与旋翼位置关系Fig.17 Position relationship between transceiver radar and rotor

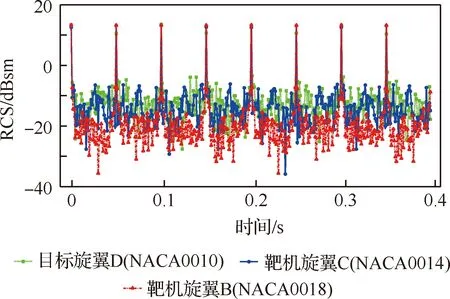
图18 不同旋翼时域动态RCS分布图(偶数片)Fig.18 Dynamic RCS profile of different rotors in time domain (even blades)

至此，在10 GHz、垂直极化雷达波条件下，对于NACA0010翼型的目标旋翼D，由NACA0014翼型的靶机旋翼C和NACA0018翼型的靶机旋翼B能够较好地模拟出相似的雷达最大微多普勒频移特征和RCS强度特征，但这两个特征是针对频域和时域分开进行模拟，仍需要对于三副旋翼的动态RCS时频域特性进行综合分析，确定最适合的靶机旋翼相似性设计方案。

分别提取出3副旋翼时频域谱的零频处时域曲线和=0.1 s时的频域曲线，如图19所示。可以看到，靶机旋翼C的时域曲线变化与目标旋翼D更为接近，旋翼B时域曲线震荡较为剧烈，但它们总体变化趋势一致；在频域曲线上，旋翼D和旋翼B在零频附近的分量幅值均高于其他频率分量的幅值，在零频附近出现了闪烁点，但旋翼C的零频分量幅值是极小值，与目标旋翼D的频域特征相差较大。综上所述，虽然6片桨叶的旋翼C和4片桨叶的旋翼B均能模拟出8片桨叶的旋翼D的频域雷达最大微多普勒频移特征和时域动态RCS强度特征，但将时域、频域联合进行分析时，旋翼B的RCS时频闪烁点特征显然更接近于旋翼D，可以更好地模拟目标旋翼的雷达散射特性，且RCS强度相似误差在0.408 dB以内。

图19 不同旋翼的时域/频域展开曲线(偶数片)Fig.19 Time/frequency domain curves of different rotors (even blades)

为了验证本节方法能否应用于奇数片桨叶旋翼的RCS强度相似性设计，以表4中旋翼E(采用NACA0010翼型)作为目标旋翼，建立分别采用NACA0010、NACA0012、NACA0014、NACA0016、NACA0018和NACA0020这6种翼型的旋翼F，计算它们在10 GHz、垂直极化雷达波照射下的水平面RCS均值对比如图20所示。

图20 RCS均值随翼型厚度变化规律(奇数片)Fig.20 Mean RCS varying with airfoil thickness(odd blades)

图20中横线代表的是目标旋翼E的RCS均值(-5.127 dBsm)，旋翼F的RCS均值随着翼型厚度的增加而增加，当旋翼F采用NACA0016翼型时，RCS均值为-5.196 dBsm，与目标旋翼最接近。鉴于此，作出目标旋翼E和NACA0016翼型的靶机旋翼F的时域动态RCS分布如图21所示。

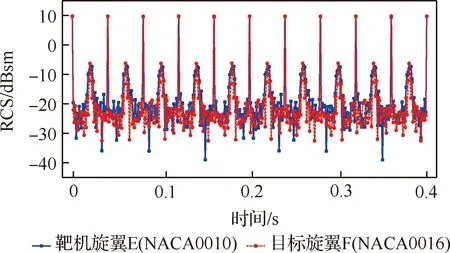
图21 不同旋翼时域动态RCS分布图(奇数片)Fig.21 Dynamic RCS profile of different rotors in time domain(odd blades)

由图21可以看出，靶机旋翼与目标旋翼的时域动态RCS幅值基本一致，RCS强度随时间的变化规律相吻合。再进一步综合分析两副旋翼的RCS时频域特征，分别提取出它们时频域谱的零频处时域曲线和=0.2 s时的频域曲线，如图22所示。

从图22中可以看出，旋翼E和旋翼F频域的雷达微多普勒特征和时域的RCS强度均吻合较好，因此针对5片NACA0010翼型桨叶的目标旋翼E，选取3片NACA0016翼型桨叶的靶机旋翼F，能够模拟出相似的动态RCS特征，且RCS强度相似误差在0.069 dB以内。

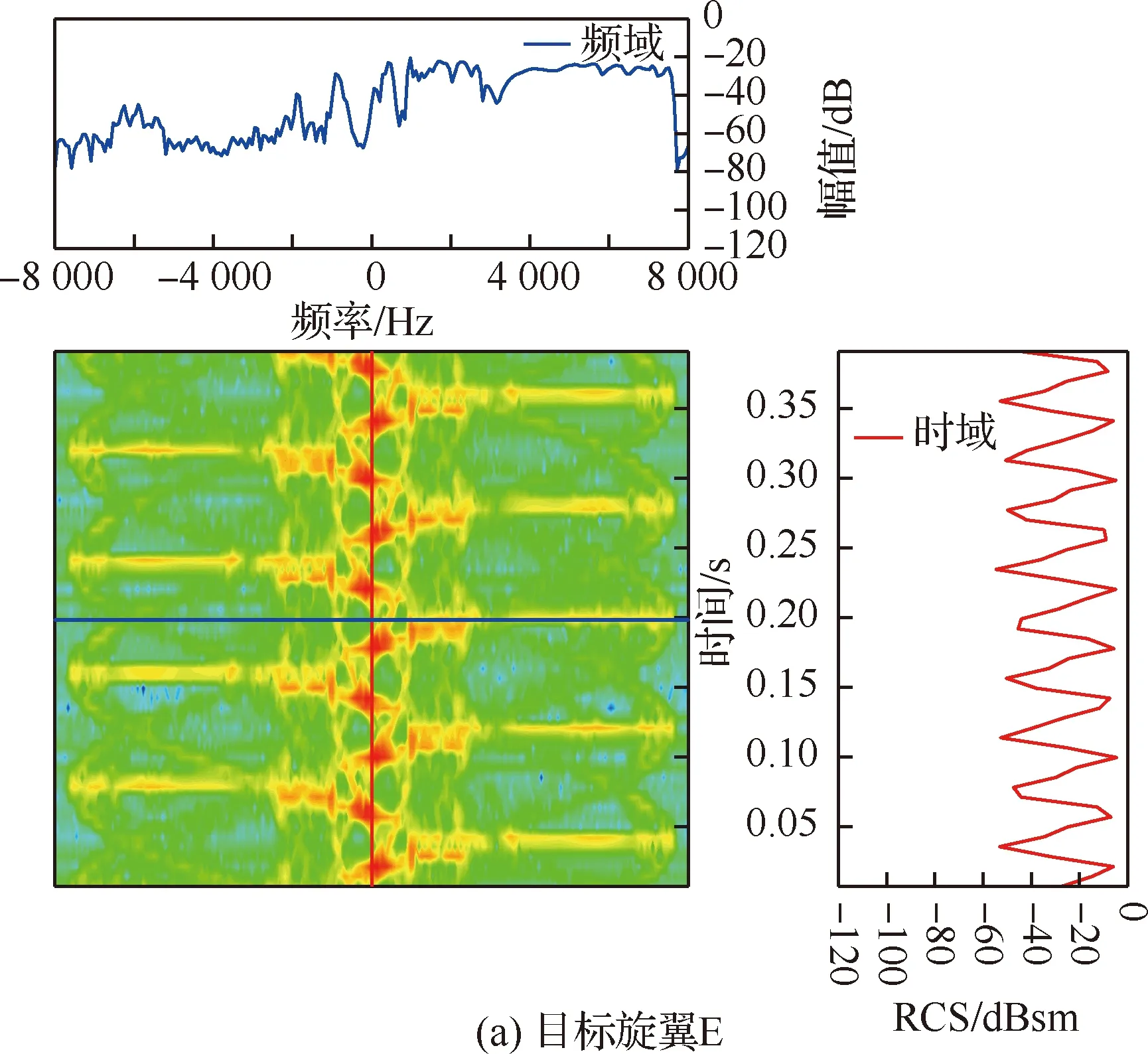
图22 不同旋翼的时域/频域展开曲线(奇数片)Fig.22 Time/frequency domain curves of different rotors(odd blades)

因此，靶机旋翼与目标旋翼的相似性设计是一个综合对比不同设计方案下旋翼动态RCS时频特征的择优过程。

本文在进行靶机旋翼的相似性设计时，兼顾旋翼气动性能，主要对动态RCS特性进行模拟，具体设计流程如图23所示。

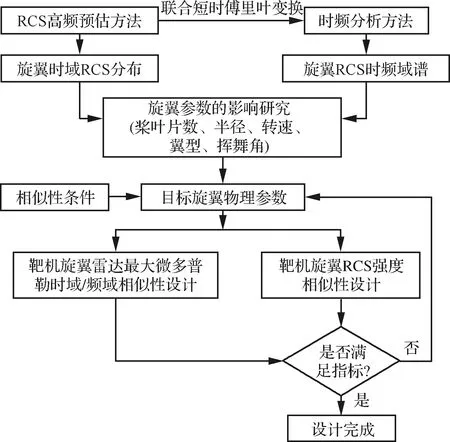
图23 基于动态RCS特征相似的靶机旋翼设计流程Fig.23 Design process of target rotor based on similar dynamic RCS characteristics

4 结 论

本文建立了基于动态RCS时频域特征相似的靶机旋翼设计方法，得出以下结论：

1) 旋翼雷达回波信号时频特性中的雷达最大微多普勒频移特征以及动态RCS强度特征与旋翼参数紧密相关：桨叶片数、半径和转速任意一个参数的改变都将引起两个特征的显著变化；翼型厚度的改变会影响RCS强度，但对微多普勒特征影响甚微；翼型弯度和挥舞角的改变对旋翼散射特性影响较弱，在相似性设计中可以不考虑这两个参数。

2) 推导了不同旋翼雷达最大微多普勒频移特征的相似性条件，验证了基于目标旋翼的已知参数，可以通过构造靶机旋翼的基本参数，实现雷达最大微多普勒频移的相似性设计。

3) 以时间推进的方式，在雷达最大微多普勒频移相似性设计完成的基础上，改变靶机旋翼翼型厚度可以实现对目标旋翼的动态RCS强度相似性模拟，再综合对比它们的RCS频域、时域特征，能够进一步提出模拟目标旋翼雷达散射特性的择优方案，并达到了最大微多普勒频移相同、RCS强度相似性误差小于0.408 dB的设计效果。

通过本文建立的相似性设计方法，能够实现直升机靶机旋翼对目标旋翼动态RCS特征的模拟，提高靶机模拟真实目标的逼真程度，有利于精确评估防御武器的作战性能。但由于靶机旋翼的设计是一项需要综合考虑气动、电磁等多方面特性的任务，而本文提出改变靶机旋翼转速和桨叶厚度，在使用过程中可能会增加对动力系统的要求，并导致阻力激增，所以，若要将本文的方法应用于实际中，仍需对目标旋翼、靶机旋翼的真实性能进行测试验证。