地铁永磁牵引系统复矢量电流环稳定性研究*

沐俊文 葛兴来 朱 丹

(1. 西南交通大学电气工程学院 成都 611756； 2. 中车大连机车车辆有限公司 大连 116022)

1 引言

随着内置式永磁同步电机(Interior permanent magnet synchronous motor，IPMSM)驱动技术的发展，IPMSM因其功率密度高、电流响应快、转矩脉动低等优点被轨道交通等领域广泛使用。但IPMSM具有非线性、强耦合的特点，dq轴系下的IPMSM数学模型，含有交叉耦合项，且随着电机转速的升高，耦合影响加剧，严重影响了控制性能[1-2]，为消除交叉耦合项的影响，可用复矢量的分析方法对IPMSM及电流控制环进行建模，并利用零极点对消原理设计复矢量电流调节器，通过引入随速度变化的复零点抵消电机模型中的复极点耦合项，实现了对定子电流励磁分量和转矩分量的有效解耦，从根本上改善了电流环的耦合特点[3-4]。

对于地铁永磁牵引系统，其具有以下特点：① 牵引变流器功率大、开关频率低、电压利用率高、脉宽调制(Pulse width modulation, PWM)技术特殊；② 牵引电机运行工况复杂、变频范围宽、电机参数多变、转矩控制难度大；③ 牵引电传动系统在复杂、恶劣的线路运行条件下稳定性要求高。为降低开关损耗，保证散热，提升逆变器效率，开关频率往往限制在1 kHz以内。研究指出随着开关频率的降低会使延时效应加剧，在电流环控制回路中引入相位滞后，进一步加剧耦合效应的影响，恶化电流环的解耦性能，从而降低系统的控制性能，甚至破坏系统稳定性[5-6]。为解决这一问题，文献[7-8]在同步旋转坐标系下，建立了永磁同步电机及其电流控制环的闭环传递函数，利用根轨迹法分析了数字控制延时对稳定性的影响，并引入了角度补偿消除了数字控制延迟的影响。文献[9-10]注意到离散控制器处理数字控制延时的优势，在离散域下建立了永磁同步电机的数学模型，并设计了复矢量PI电流调节器，分析了信号采样延迟和PWM发波延迟的影响，实现了在高速条件下的d轴和q轴电流分量的解耦控制，改善了运行在低载波比条件下IPMSM的控制性能。

然而，上述研究中未考虑到在地铁永磁牵引系统的应用背景下，载波比低以及变速带载的复杂工况，因此，本文将探究其对IPMSM复矢量电流调节器稳定性的影响并给出稳定性边界条件。据此，本文在第2节中首先推导了基于复矢量电流控制器的IPMSM电流环闭环传递函数，其次在第3节中，依据电流环闭环传递函数分析了数字延时对控制系统稳定性的影响，并给出了稳定边界条件。然后在第4节中，线性化永磁同步电机机械运动方程，推导了系统闭环传递函数，绘制其零极点分布图，并分析了不同工况下的稳定边界条件。最后在第5节中，测试验证了所推导的稳定边界条件的准确性。

2 电流环-IPMSM建模分析

2.1 IPMSM复矢量控制数学模型

考虑到IPMSM在dq轴下定子电压方程不对称的特点，采用磁链方程

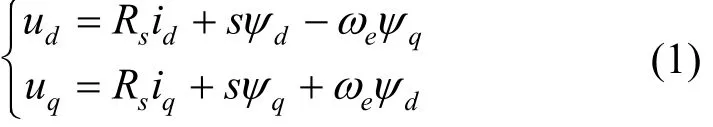
为保证矩阵的对称性，忽略电阻压降和ωeφf项，得到IPMSM模型，其复矢量形式表示为[11-12]

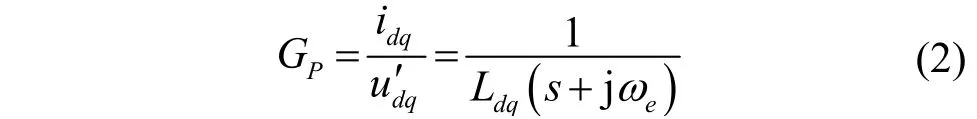
式中，u′dq=ud+juq，idq=id+jiq，ud为定子电压的d轴分量；uq为定子电压的q轴分量；id为定子电流的d轴分量；iq为定子电流的q轴分量；ωe为电机的电角速度；Ldq为定子电感；φf为永磁体磁链。

由式(2)可知，IPMSM近似为感性负载，且随着ωe的上升，dq轴耦合加剧，进而影响电流环控制性能，甚至破坏控制系统稳定性。

为保证电流环良好的解耦效果，采用零极点对消原理，复矢量电流调节器传递函数为

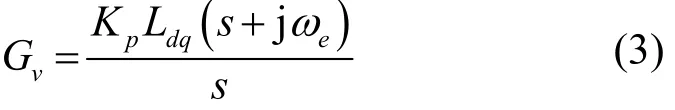
式中，Kp为控制器系数。最后在控制器输出补偿电阻压降和ωeφf项便可以得到实际的控制输出。

在数字控制系统中，存在由模数转换、数字处理器计算和PWM发生器[13]而产生的时间延迟。对于对称规则调制，从采样时刻到更新时刻[14]持续1个载波周期Ts，零阶保持效应使更新后的占空比保持不变，近似于一半Ts[15]，因此总的延迟可近似为1.5Ts[16]。由数字控制引起的控制延时和采样延时可表示为

式中，Td为逆变器的开关周期。

在低载波比情况下，电机控制中坐标变换时所采用的电角度经过采样、计算延迟已经与真实电角度存在角度滞后，再经过SVPWM生成电压矢量作用到控制器时，此时dq轴已旋转角度θd，即采样时dq轴与电压矢量实际作用时dq轴之间的夹角为数字控制延时导致的角度延迟。对于矢量控制由于控制延时而在坐标变换中引入的角度延迟，可表示为

式中，θd=ωeTd，为延迟角度。其受到电机的电角速度和逆变器开关周期的影响，如图1所示，随着ωe和Td的增大，延迟角度增大。

以两相静止坐标系和两相旋转坐标系变换为例，由于延迟角度的影响，可表示为

由式(6)可知，随着低开关频率引起的角度延迟的增大，导致dq轴耦合加剧，进一步影响电流环控制性能。

图1 ωe和Td对延迟角度的影响

综上，IPMSM复矢量电流调节器控制框图如图2所示。

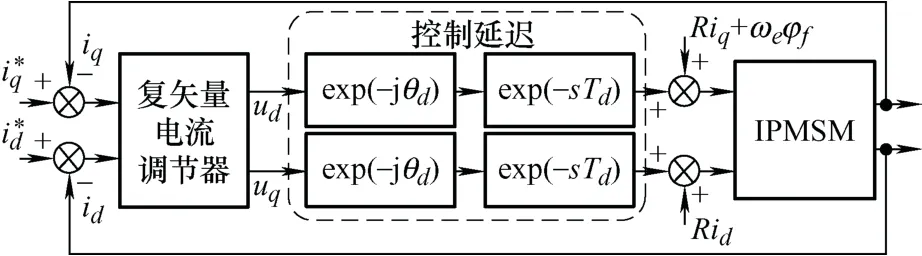
图2 IPMSM复矢量控制框图

2.2 动态解耦性能分析

如基于复矢量的电流环控制框图所示，在不考虑控制延时的情况下，由式(2)、(3)得到，系统闭环传递函数为

由式(6)可知，由于在电流控制器的传递函数中引入了与IPMSM交叉耦合项相同的复零点，与电机模型中的复极点对消，使系统闭环传递函数中不再含有耦合项，并化简为一阶惯性环节，其带宽由控制器参数Kp决定。通常为保证控制器性能，选择Kp≤0.1/Td[17]。

为直观展现零极点的变化规律，根据式(7)以及表1所示的电机参数，给定Kp=10，画出电角速度ωe由0 rad/s上升至754 rad/s时，系统闭环传递函数零极点随转速变化的零极点图，如图3所示，图中“×”表示极点，“○”表示零点。

表1 IPMSM参数

由图3可以看出，位于虚轴上的电机模型复极点与电流控制器复零点(0，-ωe)，随转速变化仍能一一对消，主导极点为(-Kp，0)，即控制系统性能由Kp决定。

图3 Gvp零极点图

3 考虑数字控制延时的稳定性分析

3.1 失稳机理分析

为探究IPMSM控制系统在数字控制延时影响下的失稳机理，分别讨论时间延时和角度延时对系统稳定性的影响。当只考虑时间延时Gt时，由式(4)、(7)得到，系统闭环传递函数为

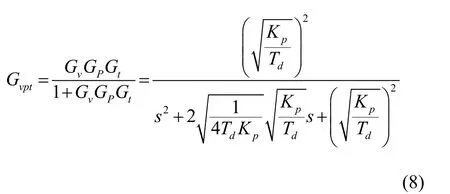
由式(8)可知，化为标准形式后，系统阻尼比可表示为

自然频率可表示为

综上可知，由于阻尼比恒大于零，系统稳定，同时系统性能可通过调节Kp以实现阻尼比的合理配置。

当只考虑角度延时Gd时，由式(5)、(7)得到，系统闭环传递函数为 可得其闭环极点为

可得，当闭环极点的实部为正时，系统失稳，即当3π/2+2kπ＞θd＞π/2+2kπ (k=0, 1, 2, 3, …)时，系统失稳。

综上，在假设条件下，分别考虑了时间延迟与角度延迟单独作用下的闭环传递函数稳定性，可知，在完全解耦情况下，控制延迟依然可能致使系统失稳，失稳的根本原因是角度延迟在(π/2+2kπ, 3π/2+2kπ)区间内产生了实部为正的极点。

3.2 稳定性边界条件

然而，在实际控制系统中，控制延迟包括的时间延迟和角度延迟同时存在，因此，进一步分析GtGd共同作用下的影响。此时，系统闭环传递函数可表示为

可得其闭环极点为

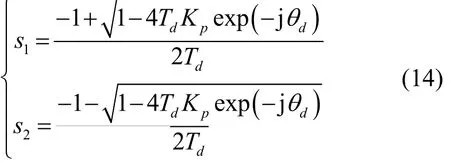
由闭环极点可知，s2＜0恒成立，可得稳定边界条件为

为直观地说明闭环极点的分布规律，依据表1所示的电机参数，绘制在不同条件下的系统闭环传递函数Gvpdt零极点分布图。

(1) 电角速度ωe对零极点的影响。给定Kp=10，Td=1/1 000不变的条件下，逐渐增大ωe(由200 rad/s增至1 675 rad/s)，Gvpdt零极点分布如图4所示。由图4可知，电流环完全解耦后，在数字控制延时的影响下，电流环闭环传递函数存在两个极点分别为s1和s2，且s1距离虚轴更近，为主导极点。随着ωe的增加，θd随之增加，闭环极点s1向右半平面移动，当ωe达到1 570 rad/s左右时，系统失稳，此时，θd约为π/2。

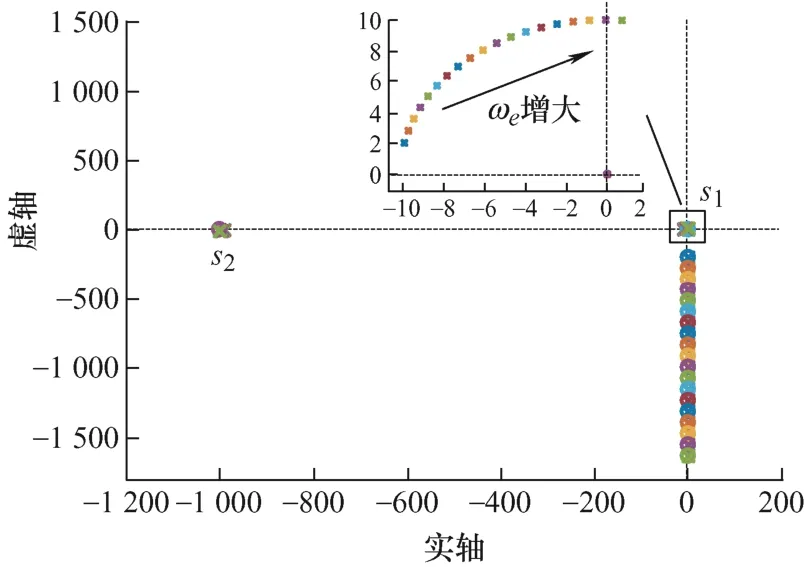
图4 Gvpdt零极点图

(2) 控制带宽Kp对零极点的影响。给定Td=1/1 000，ωe=754 rad/s不变的条件下，逐渐增大Kp(Kp≤0.1/Td)，Gvpdt零极点分布如图5所示。由图5可知，随着Kp的增加，主导极点s1向左半平面移动，利于系统稳定。

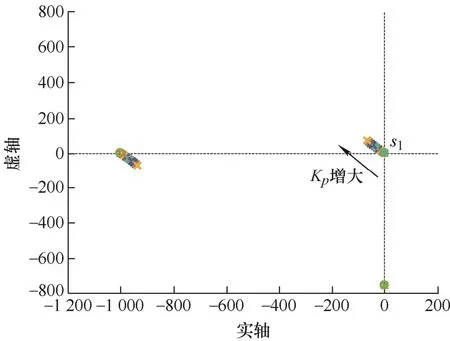
图5 Gvpdt零极点图

(3) 逆变器开关周期Td对零极点的影响。给定Kp=10，ωe=754 rad/s不变的条件下，逐渐增大Td(由0.001 s增至0.002 2 s)，Gvpdt零极点分布如图6所示。由图6可知，随着Td的增加，θd同时增大，闭环极点s1、s2均向右半平面移动，但主导极点仍为s1，当Td达到0.002 s左右时，系统失稳，此时θd约为π/2。

综上分析，式(13)所示系统闭环极点无法得到失稳边界条件的准确解析解，结合零极点分布规律可知，在采用复矢量控制电流环完全解耦情况下，角度延迟导致系统失稳的边界条件可近似为

4 不同工况下的稳定性分析

为进一步探究不同工况对IPMSM复矢量电流调节器稳定性的影响，可根据IPMSM数学模型，建立电机负载转矩和电角速度之间的传递函数。首先，根据式(2)改写IPMSM模型，并线性化，可得

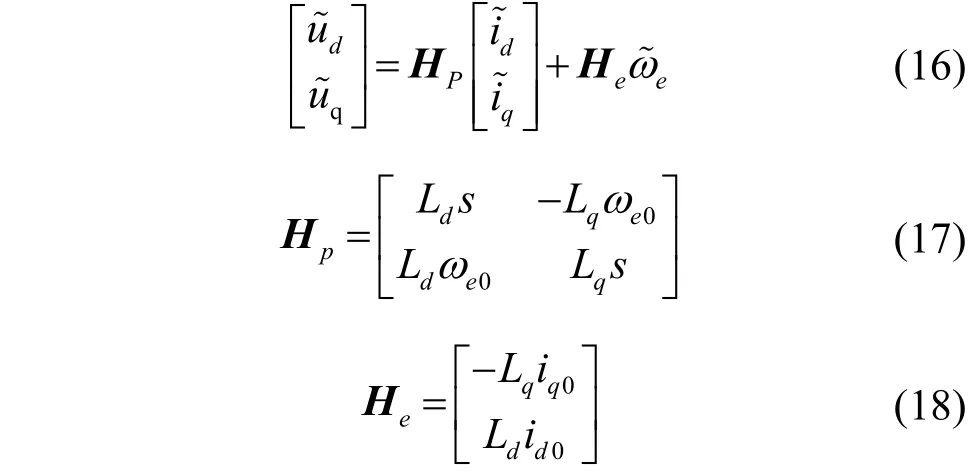
式中，下标“0”表示稳态分量；上标“～”表示扰动分量。

IPMSM机械运动方程可表示为

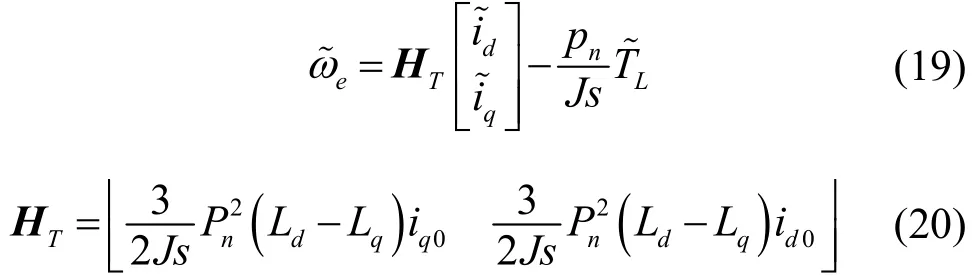
式中，J为转动惯量；pn为IPMSM的极对数。

其次，根据式(3)可得复矢量电流调节器矩阵形式，并线性化，表示为

联立式(16)～(22)可得电机负载转矩和电角速度之间的传递函数，表示为

若进一步考虑式(4)、(5)所示延时环节的影响，可将式(23)进一步推导得到

依据表1所示的IPMSM参数，绘制式(23)、(24)所示的闭环传递函数在不同工况下的零极点分布图。

4.1 不同负载对稳定性的影响

给定Kp=100，ωe=314 rad/s，Td=1/1 000不变的条件下，逐渐增大所带负载(由0 N·m增至900 N·m)，稳态时，由于电机电磁转矩Te0与负载转矩TL相等，因此，根据电磁转矩计算公式

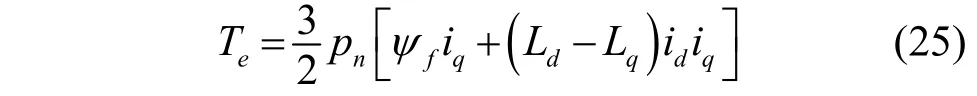
可知，随着所带负载的增大，电机稳态运行时dq轴电流随之增大。Gωl和Gωld零极点分布分别如图7、8所示。结合式(23)和图7可知，Gωl存在三个零点分别为(0，jωe)、(0，-jωe)和(-Kp，0)，以及(0，0)极点和分别分布在三个零点周围的三个极点，其中分布在(0，jωe)和(0，-jωe)零点周围的两个极点s3和s4距离虚轴距离更近为主导极点，Gωl零极点分布符合基于零极点对消的复矢量电流环控制原理。同理，结合式(24)和图8可知Gωld同样存在(0，0)极点和分布在(0，jωe)和(0，-jωe)零点周围的两个主导极点s5和s6。

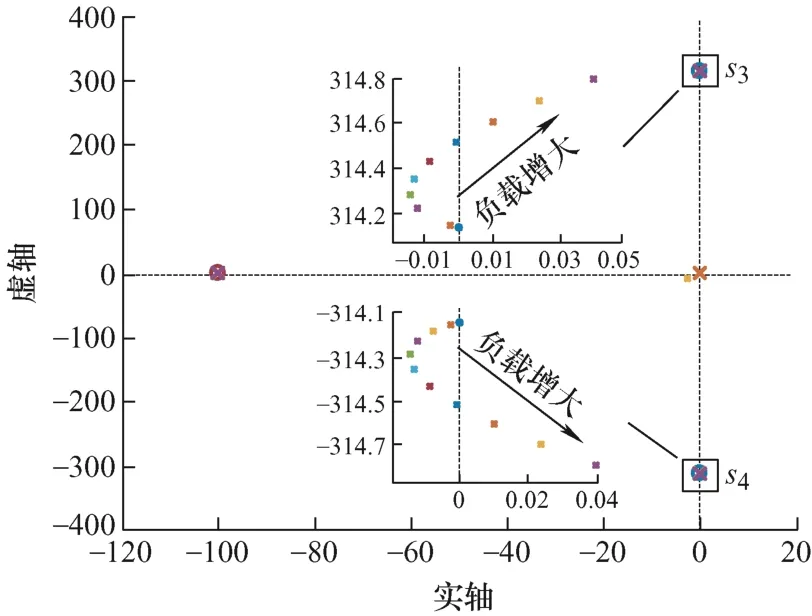
图7 Gωl零极点图

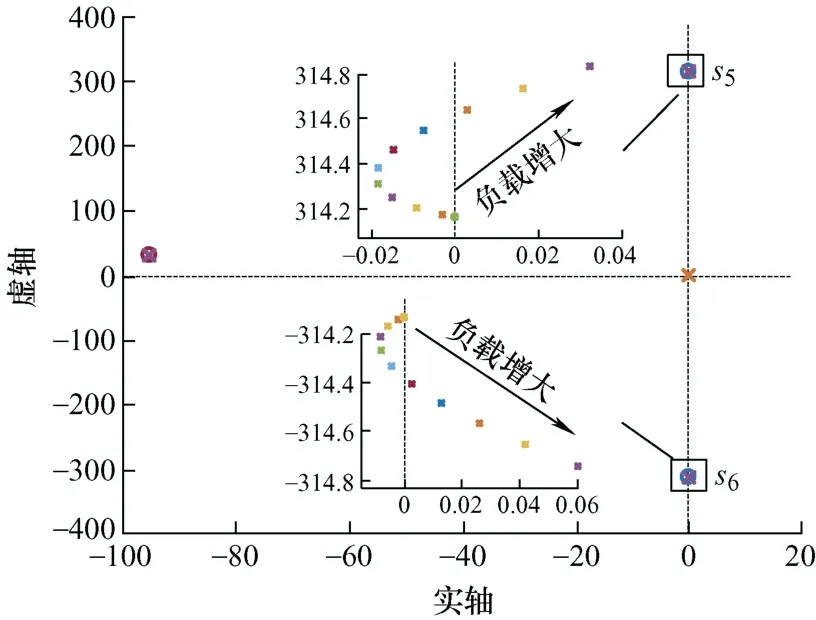
图8 Gωld零极点图

由图7可知，在不考虑延时环节影响的条件下，随着带载的增加，主导极点s3和s4先向左半平面移动再向右半平面移动，当带载达到637 N·m左右时，s3和s4同时越过虚轴，系统失稳。由图8可知，在延时环节的影响下，随着带载的增加，主导极点s5和s6仍先向左半平面移动再向右半平面移动，但由于延时环节的影响，当带载达到510 N·m左右时，s6首先越过虚轴，系统失稳。

从零极点图上看，延时环节的引入使系统极点受到exp(-sTd)的影响向虚轴靠近同时受到exp(-jθd)的影响向正半区域移动进而使失稳边界收缩，系统更易失稳。延时的增加使得生成的控制信号产生了滞后和偏差，稳态运行时，主要由于延迟角而使得坐标变换产生误差，时间延时而使得交流控制信号产生滞后，进而加剧系统耦合，破坏电流环解耦能力，促使系统失稳。据此，在延时环节的影响下，电机带载能力下降，更易失稳。

4.2 电角速度ωe对稳定性的影响

给定Kp=100，Td=1/1 000，带900 N·m恒定负载不变的条件下，逐渐增大电机转速(由ωe=30 rad/s增至ωe=314 rad/s)，Gωl和Gωld零极点分布分别如图9、10所示。

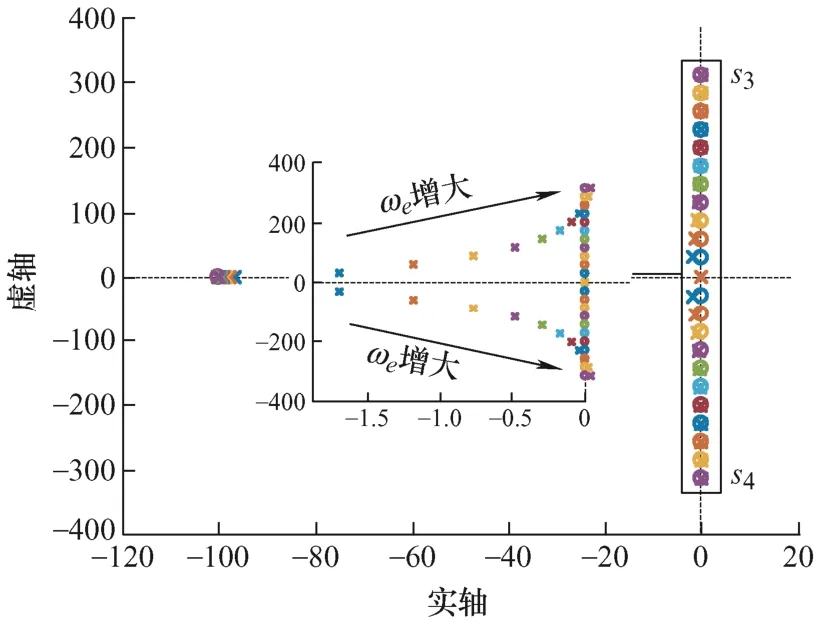
图9 Gωl零极点图

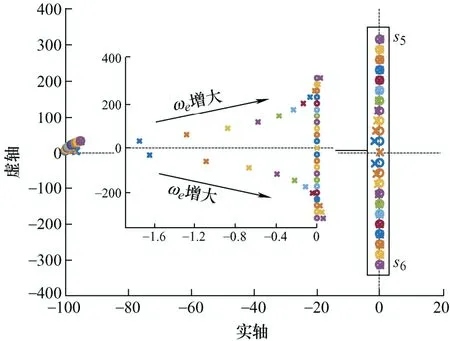
图10 Gωld零极点图

由图9可知，在不考虑延时环节影响的条件下，随着电机转速的增加，主导极点s3和s4沿虚轴逐渐远离实轴并向正半平面移动，当电机转速上升到259 rad/s左右时，s3和s4同时越过虚轴，系统失稳。相反，随着电机转速的降低，主导极点s3和s4逐渐偏离零点(0，jωe)和(0，-jωe)，此时零极点难以相消，复矢量电流环难以实现完全解耦。由图10可知，在延时环节的影响下，随着电机转速的增加，主导极点s5和s6仍有相同的运动趋势，但由于延时环节的影响，当电机转速上升到230 rad/s左右时，s6首先越过虚轴，系统失稳。据此，电机带载时复矢量电流环解耦能力恶化。在延时环节的影响下，复矢量电流环解耦能力进一步恶化，电机调速范围更窄，更易失稳。

4.3 控制带宽Kp对稳定性的影响

给定ωe=314 rad/s，Td=1/1 000，带500 N·m恒定负载不变的条件下，逐渐增大控制带宽Kp(Kp≤0.1/Td)，Gωl和Gωld零极点分布分别如图11、12所示。

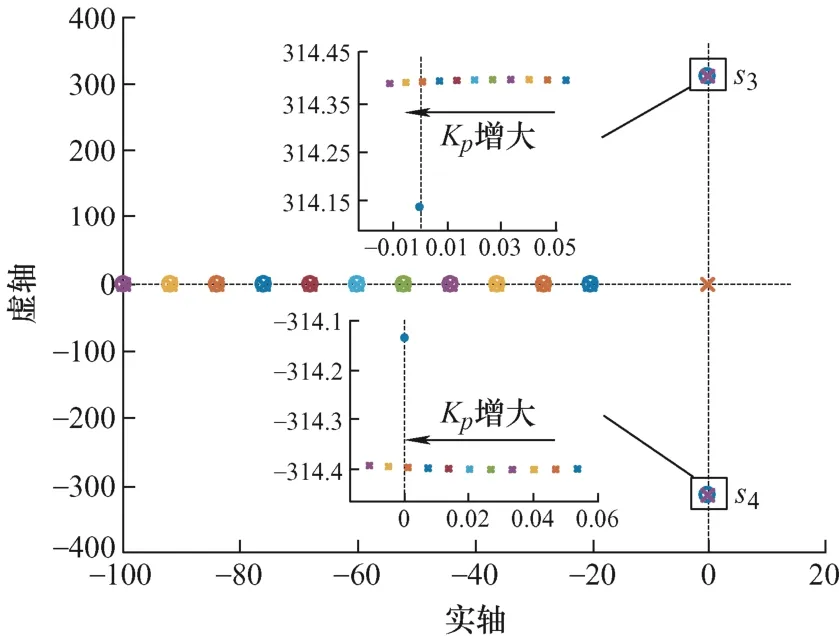
图11 Gωl零极点图

图12 Gωld零极点图

由图11可知，在不考虑延时环节影响的条件下，随着控制带宽的增加，主导极点s3和s4向负半平面移动，当控制带宽增加到85左右时，s3和s4同时越过虚轴，系统稳定。由图12可知，随着控制带宽的增加，主导极点s5和s6虽有相同的运动趋势，但由于延时环节的影响，当控制带宽增加到98左右时，s6才越过虚轴，系统稳定。据此，随着控制带宽的增加，电机带载能力上升。但在延时环节的影响下，抑制了电机带载能力上升。

5 测试验证

为验证第2、3节中所探讨的失稳边界条件的准确性，在如图13所示的硬件在环测试平台上进行测试验证，测试平台由上位机、DSP28335以及实时仿真器组成，其中控制算法下载到TMS320F28335DSP中实现，直流电源、滤波环节、逆变器和IPMSM则由实时仿真器模拟运行实现。电机参数与控制算法与第2～4节中所使用的一致，测试工况均在额定范围内。

图13 硬件在环测试系统框图

5.1 空载工况下稳定性边界条件验证

为测定被测系统的稳定性边界条件，验证所述理论的正确性，首先给定试验参数Kp=10，Td=0.004 s不变的条件下，逐渐增大ωe并观测记录电机运行状态，如图14所示，当被测系统由稳定变为失稳时即可测得稳定的边界条件。据此，从图14中可以看出，随着ωe的增大，电机逐渐失稳振荡，此时ωe在398 rad/s左右，θd约为π/2，与第2节中所分析的 一致。

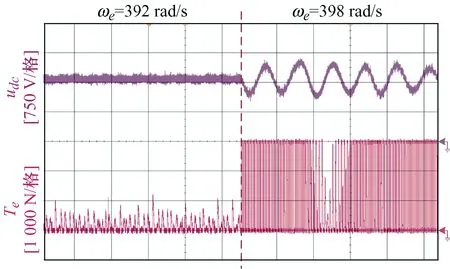
图14 电机响应

同理，给定Kp=10，ωe=398 rad/s不变的条件下，逐渐增大Td并观测记录电机运行状态，如图15所示。从图15中可以看出，随着Td的增大，电机逐渐失稳振荡，此时Td在0.004 s左右，θd约为π/2。

图15 电机响应

5.2 带载工况下稳定性边界条件验证

采用与第5.1节相同的方法，给定Kp=100，ωe=314 rad/s，Td=1/1 000不变的条件下，逐渐增大所带负载并观测记录电机运行状态，如图16所示。从图16中可以看出，随着所带负载的增大，电机逐渐失稳振荡，此时负载在500 N·m左右。

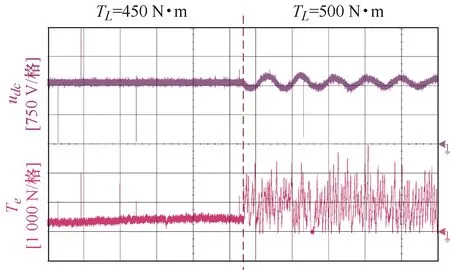
图16 电机响应

给定Kp=100，Td=1/1 000，带900 N·m恒定负载不变的条件下，逐渐增大电机转速并观测记录电机运行状态，如图17所示。从图17中可以看出，随着电机转速的增大，电机逐渐失稳振荡，此时ωe在230 rad/s左右。

图17 电机响应

给定ωe=314 rad/s，Td=1/1 000，带500 N·m恒定负载不变的条件下，逐渐减小控制带宽Kp并观测记录电机运行状态，如图18所示。从图18中可以看出，随着控制带宽的减小，电机逐渐失稳振荡，此时Kp在98左右。

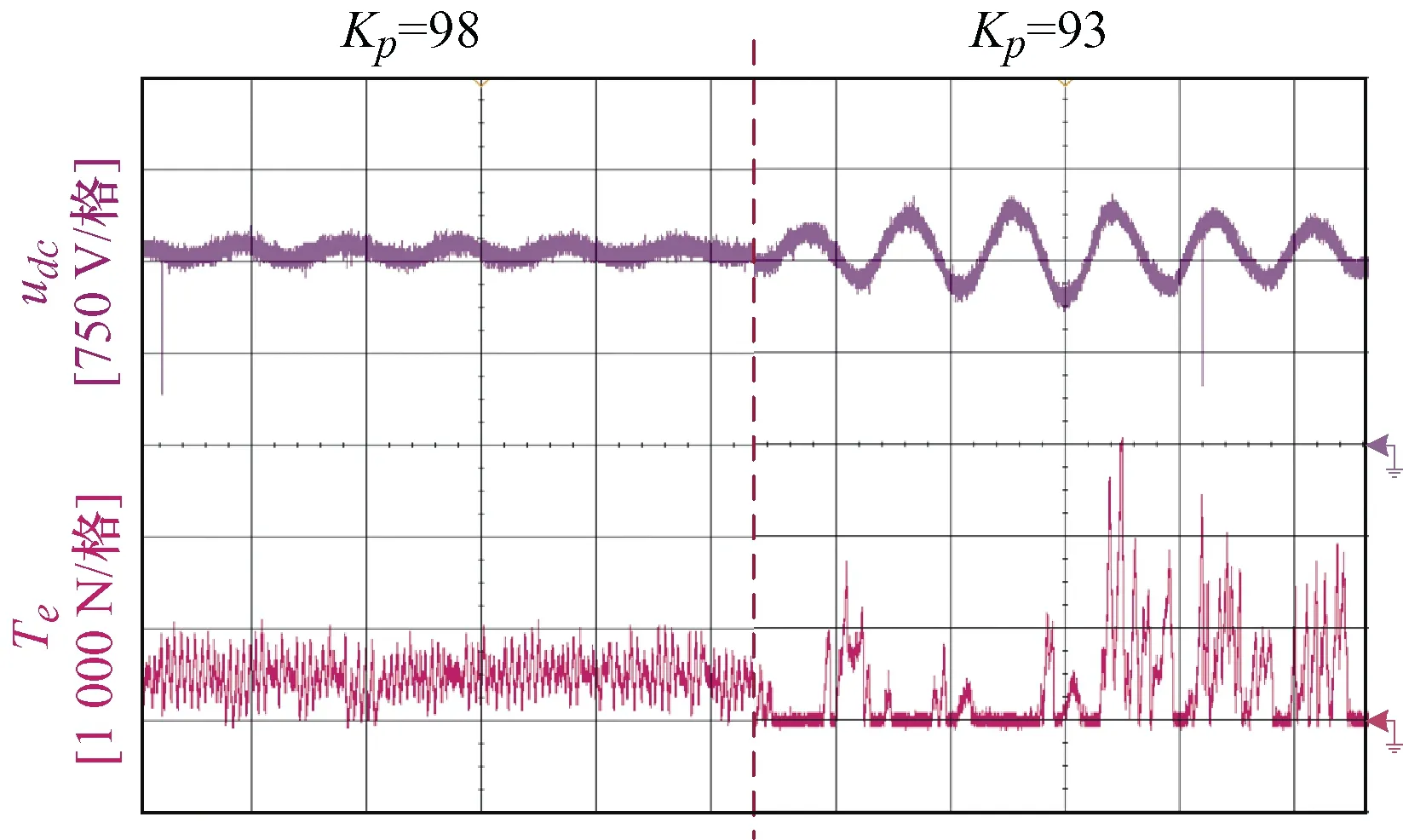
图18 电机响应

综上，第2、3节中的理论分析与试验结果一致，验证了稳定性分析结果的准确性。

6 结论

本文推导了基于复矢量电流控制器的IPMSM电流环闭环传递函数，并依据电流环闭环传递函数求解出系统闭环极点的解析解，利用零极点分布图，分析了各参数对系统稳定性的影响，其主要结论 如下。

(1) 即使在完全解耦的情况下，控制延迟依然可能致使系统失稳，失稳的根本原因是角度延迟在(π/2+2kπ, 3π/2+2kπ)区间内产生了实部为正的极点。

(2) 结合零极点分布规律可知，ωe和Td的增大均会使θd增加，进而不利于系统稳定，而Kp(Kp＜0.1/Td)的增加会增大系统带宽，利于系统稳定。在采用复矢量控制电流环完全解耦情况下，角度延迟导致系统失稳的边界条件可近似为

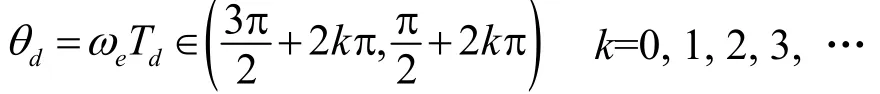
(3) IPMSM带载时复矢量电流环的解耦能力会恶化，虽然增加控制带宽可以提升电机的带载能力，但在延时环节的影响下，复矢量电流环解耦能力进一步恶化，电机调速范围更窄，电机带载能力下降，更易失稳。