低速区列车牵引系统的电制动力提升控制方法*

李建新 李佳耀 高 翔 蒋 威, 宋文胜

(1. 西南交通大学电气工程学院 成都 611756； 2. 中国铁道科学研究院集团有限公司机车车辆研究所 北京 100081； 3. 北京纵横机电科技有限公司 北京 100094)

1 引言

列车牵引传动系统在运行过程中包括两个核心工况：牵引工况和制动工况。随着列车速度的不断提高，如何让列车在满足制动距离、制动舒适性以及可靠性的前提下进行快速有效的制动成为研究人员关注的热点[1]。目前，我国轨道交通车辆的主流制动方式为电-空联合制动[2-3]，其具体流程如下：当列车运行在中高速时，以电气制动(再生制动)为主，当列车制动至低速(10 km/h)以下时，会逐渐切除再生制动并投入空气制动直至列车可靠停车[2]，电-空联合制动特性曲线如图1所示。

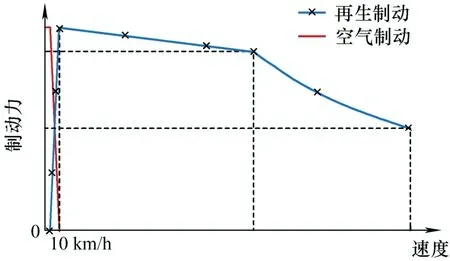
图1 电-空联合制动特性曲线

再生制动通过控制牵引电机工作在再生制动工况即可实现，同时再生制动还可以将减速过程中的动能转换为电能经牵引变流器回馈至牵引网[4-5]，是一种理想的电气制动方式；但空气制动是一种机械制动方式，通过闸瓦与制动盘间的摩擦将车辆减速过程中的能量以热量的形式耗散掉[6]，所以电-空联合制动有着其本身无法克服的缺点，如下所示。

(1) 电气制动和空气制动在切换时可能会引起加速度的突变，乘客舒适性下降[7]。

(2) 空气制动可控性不强，响应速度慢，电气制动与空气制动切换后易造成停车位置不准确[7-8]。

(3) 空气制动会造成制动盘和制动闸瓦的磨损，后期维护成本高[7-8]。

为解决电-空联合制动所存在的问题，最早应用在航空领域的电机械制动(Electromechanical brake, EMB)被应用在轨道交通领域，EMB通过电机驱动闸瓦与制动盘摩擦，虽然在制动信号传递和制动力控制上都摆脱了压力空气等介质，可控性有所提高，但仍是通过摩擦来实现列车的制动[9-10]。为充分利用牵引电机制动的优越性，日本学者SONE等[11-12]在1998年前后提出了全电制动的概念，通过牵引电机工作在再生制动和反接制动工况实现了列车的全电制动，但其实现方式是基于恒压频比的标量控制；文献[13-14]对列车的全电制动技术进行了相应的介绍，然而其研究重点是通过提高测速精度来实现制动工况下的准确停车，对再生制动及反接制动在牵引传动系统中的实现方式等内容研究较少。文献[15]针对直线感应电机列车的全电制动进行了相关研究，同样采用再生制动+反接制动的方式，并在停车前引入减速冲动率控制以提高乘坐舒适度。文献[16]提到西门子的部分牵引系统具备电制动到零速的功能，但并未给出其具体的制动逻辑和制动方案。由以上文献可知，再生制动与反接制动结合的方式或许是一种全电制动解决方案，但以上文献都没有对基于矢量控制反接制动的可控性、实现原理以及再生制动与反接制动结合的具体实现方式进行研究。

为保证列车低速运行时电制动力的有效发挥，本文详细介绍了一种基于再生制动和反接制动的列车全电制动控制技术。首先根据矢量控制下电磁转矩和转差频率的关系，分析不同制动方式在低速区的转矩输出能力，确定了再生制动在定子角频率大于零和反接制动在定子角频率小于零时制动转矩的可控性；其次，通过间接矢量控制磁场定向和直接矢量控制磁链观测证明了反接制动的实现原理和可行性，进而提出由再生制动自然换向至反接制动的全电制动方案；最后，通过小功率试验验证了所提方案的有效性。

2 异步牵引电机数学模型

目前，异步牵引电机控制以转子磁场定向控制为主。根据磁场定向控制的基本原则，需要在按转子磁场方向定向的同步旋转坐标系(MT坐标系)下建立电机的数学模型。由于M轴与转子磁场旋转方向一致，故有

式中，ψr为转子磁链幅值；ψrM、ψrT分别为转子磁链在M轴和T轴的分量；Lm为定子与转子间的互感；Lr为转子自感；irM、irT分别为转子电流在M轴和T轴的分量。

此时，异步电机电压方程为

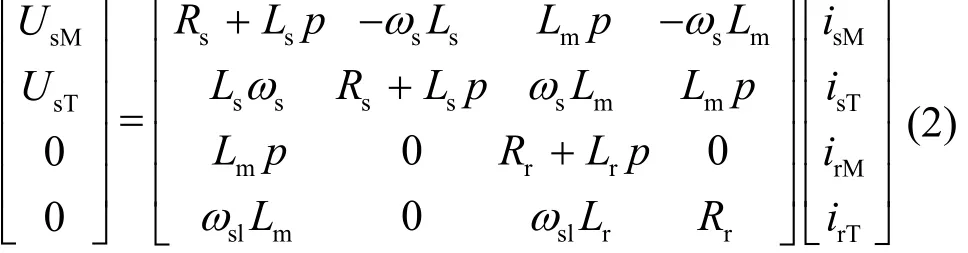
式中，UsM、UsT分别为定子电压在M轴和T轴的分量；isM、isT分别为定子电流在M轴和T轴的分量；Rs、Ls、Rr分别为定子电阻、定子自感和转子电阻；p为微分算子；ωs为定子角频率，也等于同步角频率；ωsl为转差频率。

由式(2)第三行和式(1)联立可得

式中，Tr=Lr/Rr为转子时间常数。

在满足转子磁场定向的条件下，电磁转矩为

由式(3)和式(4)可得，通过坐标变换和转子磁场定向，可以实现转子磁链和电磁转矩的解耦控制。转子磁链仅与定子电流的M轴分量有关；电磁转矩只与转子磁链及定子电流的T轴分量有关，若控制isM使转子磁链保持恒定，则通过控制isT就可以实现对电磁转矩的瞬时控制。

由式(2)第四行和式(1)联立可得

将式(5)代入式(4)可得

由式(6)可知，在矢量控制保持转子磁链恒定的情况下，电磁转矩与转差频率成正比，维持转差频率恒定，即可维持电磁转矩恒定。

3 不同电气制动方式分析

目前，常见的异步电机制动方式主要有再生制动、反接制动和直流制动三种。为了选取合适的制动方式以实现列车全电制动，现对三种制动方式进行详细的对比分析。

3.1 再生制动

当异步电机制动时，需要输出制动性质的电磁转矩(Te＜0)。当采用磁场定向控制方式时，由式(6)可知转矩与转差频率成正比，因此转差频率小于零，同步转速ns小于电机转速nm，电机工作在再生制动状态。此时转差率为s=(ns-nm)/ns＜0，电机产生制动性质的转矩，使得电机减速，如图2a所示。在再生制动工况下异步电机的电磁功率小于零，处于发电机状态，可以将列车制动过程中减少的动能转化为电能并通过四象限变流器反馈回接触网。

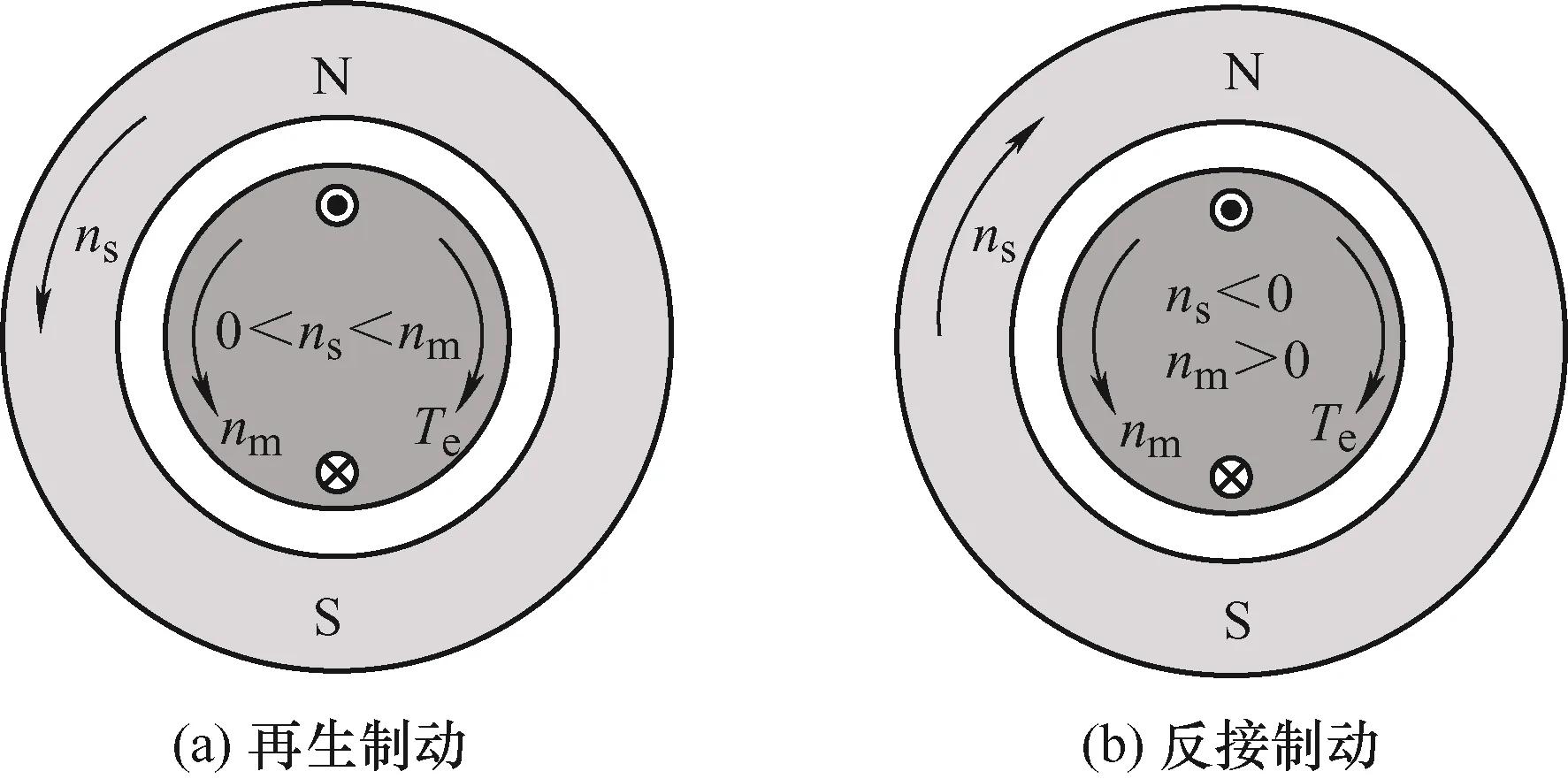
图2 再生制动和反接制动工作示意图

3.2 反接制动

当异步牵引电机工作在电动状态时，若调整定子三相电压的相序，则电机进入反接制动状态。此时定子角频率小于零，转速大于零，因此转差频率小于零，转差率大于1，产生制动性质的转矩，使得电机减速，如图2b所示。在反接制动工况异步电机的电磁功率大于零，从直流侧吸收电能，列车制动过程中减少的动能和吸收的电能在电机绕组中转换为热能消耗掉。

3.3 直流制动

直流制动又称能耗制动，一般通用变频器均具备直流制动功能[17]。当异步牵引电机工作时，若使得定子电压的频率为零，即向定子绕组中通入直流电流，则电机进入直流制动状态。此时直流电流在气隙内形成一个固定方向的磁场，转子由于惯性仍在旋转，转子绕组将切割定子磁场产生感应电动势和转子电流。根据左手定则，可确定直流制动工况下电机转矩方向与转速方向相反，可以输出制动转矩，使得电机减速，如图3所示。

图3 直流制动工作示意图

3.4 三种制动方式低速区转矩输出能力对比

通过异步牵引电机输出制动转矩实现列车的全电制动，需要电机在全速度范围内输出可控的制动转矩。在制动工况，此时异步电机制动转矩Te＜0，所以ωsl＜0，ωs可以表示为

式中，ωm为转子机械角频率，即转速。

在制动工况下，当列车速度ωm较高时，ωs＞0，为再生制动；随着列车速度降低，ωs减小，当车速降低至满足np·ωm=-ωsl时，ωs=0，若维持ωs=0，则为直流制动；如果车速继续降低，即np·ωm＜ -ωsl时，ωs＜0，则为反接制动。

已知在转子磁场定向控制中，异步电机输出转矩和转差频率成正比，如果在低速区需要有较大的制动转矩输出，就必须有较大的转差频率。下面分析低速区不同制动方式下转差频率的大小，进而判定低速区可输出制动转矩的大小。注意，由于制动转矩Te＜0，以上提到的制动转矩和转差频率实际为制动转矩的绝对值和转差频率的绝对值。

在再生制动方式下，定子角频率ωs与转速ωm均大于0，且ωs＜np·ωm。当车速较高时，由图4中0～t1阶段可知转差频率的变化范围较大，因此可以输出较大的制动转矩；随着车速逐渐降低，如图4所示，ωs首先在t1时刻降低至0 rad/s，而ωm仍大于零，此时再生制动结束，所以仅凭再生制动无法维持较大的制动转矩到零速。

如果定子角频率降为0 rad/s后继续降低转速使得定子角频率为负值，则进入反接制动方式。此时转速ωm＞0，定子角频率ωs＜0且无大小限制，如图4的t1～t2阶段所示，所以即使在车速接近零速时，转差频率ωsl依然为负，且其变化范围可调，|ωsl|可以维持较大的值，也可随制动转矩的需求而变化。此时，电机仍可实现正确的磁场定向，矢量控制结构可正常使用。因此，在接近零速，定子角频率小于零时，通过反接制动的方式可以实现制动转矩的任意可控，且再生制动和反接制动的定子角频率是连贯的，不会发生频率上的突变。

图4 低速区恒转矩制动定转子频率关系

直流制动方式时，ωs=0或在定子两相绕组中通入直流电。从直流制动的基本原理可知，直流制动需要转子绕组切割固定磁场，所以直流制动要有制动转矩的输出，电机转速必须大于零。另外，直流制动的制动转矩与通入定子绕组的直流电流大小有关，但通入的电流又不宜太大，否则会烧坏绕组。而且，直流制动不再满足矢量控制的基本原理，综合以上因素，直流制动的可控性差，可靠性低，所以不适用于大功率或频繁启停的应用场合[17-18]。

在第3.2节中提到，反接制动过程中减少的动能和吸收的电能均在电机绕组中转换为热能消耗掉。但无论异步牵引电机工作在再生制动状态还是反接制动状态，转子铜耗均可通过式(8)进行计算

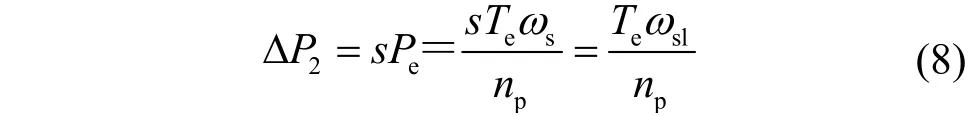
当车速较低时，一般采用恒转矩控制，所以Te为恒值；且当采用转子磁场定向的矢量控制策略时，电磁转矩与转差频率成正比，所以ωsl也为恒值。因为反接制动仍基于矢量控制，所以再生制动工况和反接制动工况的转子铜耗相同，因此，采用反接制动不会额外造成转子铜耗的增加。

4 再生制动+反接制动的全电制动

我国现有轨道交通列车牵引系统的制动特性曲线一般如图1所示。为了减小闸瓦磨损，要求在车速低于10 km/h仍能使牵引电机发挥较大的制动力，从而实现全电制动，不再需要空气制动的介入。

通过以上分析可知，仅通过再生制动的方式无法使异步牵引电机制动至零速，如果配合直流制动或反接制动的方式，可以使电机在低速区仍能够发挥出较大制动转矩使车辆制动至零速。又加上直流制动不适用于大功率场合，因此选择再生制动与反接制动相结合的方式来实现异步牵引电机的全电制动。

基于转子磁场定向的矢量控制根据磁链观测方式的不同可分为间接矢量控制和直接矢量控制，下面分别说明这两种矢量控制是如何实现再生制动到反接制动的自然换向的。

间接矢量控制一般采用磁链开环，转速和电流双闭环的控制方式。根据参考电流、给定转子磁链及转速ωm计算转子磁链的相角θ，即

在制动工况下，随着车速的降低，电机转速ωm不断减小，为了保证ω*sl＜0以输出负转矩，ω*s会由大于零的状态自行过渡至小于零的状态，从而使电机进入反接制动工况。其中，带*的符号分别为对应物理量的参考值。

直接矢量控制则采用磁链、转速和电流均闭环的控制方式。直接矢量控制需要进行转子磁链观测，以适用于低速区的电流模型为例进行说明，两相静止坐标系(αβ坐标系)下转子磁链电流观测模型为

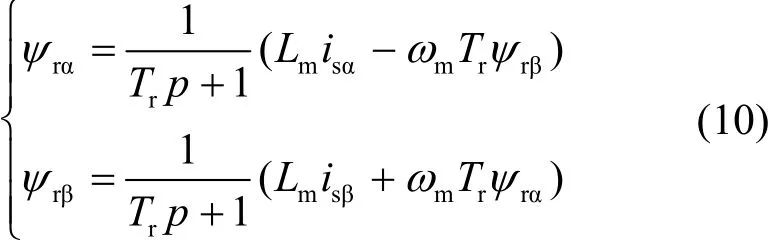
式中，ψrα、ψrβ和isα、isβ分别为转子磁链和定子电流在α轴和β轴的分量。

经后续试验验证，电机由再生制动切换为反接制动时，ψrα和ψrβ的相位会发生变化，由ψrα超前ψrβ切换为ψrβ超前ψrα，表明此时同步旋转的方向发生了变化，同步角频率ωs＜0，电机进入反接制动状态。

由以上分析可知，无论是间接矢量控制还是直接矢量控制，均可实现再生制动到反接制动的自然切换，所以基于磁场定向控制的再生制动+反接制动的全电制动方式在控制结构上无需做改动，如图5所示(以间接矢量控制为例)。

图5 间接矢量控制结构图

在以上全电制动方案具体实施时，首先要解除定子角频率大于零的限制，允许定子由正值切换为负值。在实际列车牵引传动控制系统中，对电机的定子角频率有所限制，要求其值必须大于某一正值，因此，要实现反接制动，必须解除该限制。

其次，需要对传统电-空联合制动特性曲线做修改，设计相应的全电制动特性曲线。全电制动电气制动力参考值需要按照如图6所示的全电制动特性曲线进行给定，低速区不再进行如图1所示的再生制动和空气制动切换。

图6 全电制动特性曲线

同时，为满足不同减速度的制动要求，全电制动特性曲线会有所不同，由第3.4节有关反接制动的论述可知，反接制动可以实现在低速区制动转矩任意可控，所以通过再生制动+反接制动的全电制动方式可满足不同减速度的制动要求。

此外，反接制动在速度达到零之后，可能会发生反转现象，带来安全隐患。因此，当列车速度降低至接近零速时，需要及时施加停放制动，从而实现列车的可靠停车。

5 试验验证与分析

为验证基于再生制动+反接制动的异步牵引电机全电制动方式的有效性，在小功率异步电机(Induction motor，IM)-永磁同步电机(Permanent magnet synchronous motor，PMSM)对拖试验平台上进行了验证，平台参数如表1所示，其中电机参数均为异步电机参数；试验平台主电路结构示意图如图7所示，试验平台实物图如图8所示。

表1 试验平台参数

由图7可知，两组三相两电平逆变器分别驱动IM和PMSM，其中IM是被试电机，PMSM为陪试电机(负载电机)。IM采用转速闭环的矢量控制方式，采用旋转变压器进行转速测量，PMSM采用连续集模型预测控制方法，转速环开环，直接给定转矩，尽可能为IM提供准确的负载转矩。

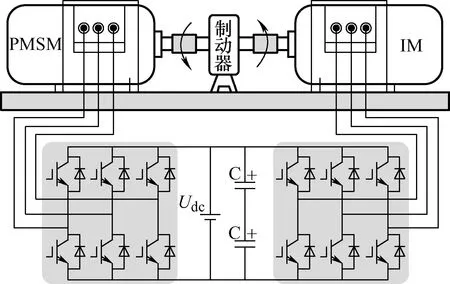
图7 试验平台主电路结构示意图

图8 IM-PMSM试验平台

由于IM和PMSM呈对拖形式，所以两者转速及转矩的正方向相反，规定图7中两个箭头的方向分别为IM和PMSM转速及转矩的正方向，若其转速和转矩与参考正方向相反，则为负值。当IM给定正向转速并采用转速闭环控制，且PMSM提供负的负载转矩时，为平衡负载转矩，IM输出制动转矩，因此，IM工作在制动状态。

5.1 反接制动转矩输出能力验证

首先，通过对拖试验验证反接制动低速区制动转矩的可控性。通过PMSM分别为IM提供-12.5 N·m、-15 N·m、-20 N·m和-22.5 N·m的负载转矩，IM给定转速为10 r/min，图9a～9d分别给出了以上各转矩下IM的A相定子电流、转速、IM制动转矩和PMSM所提供负载转矩的试验波形。

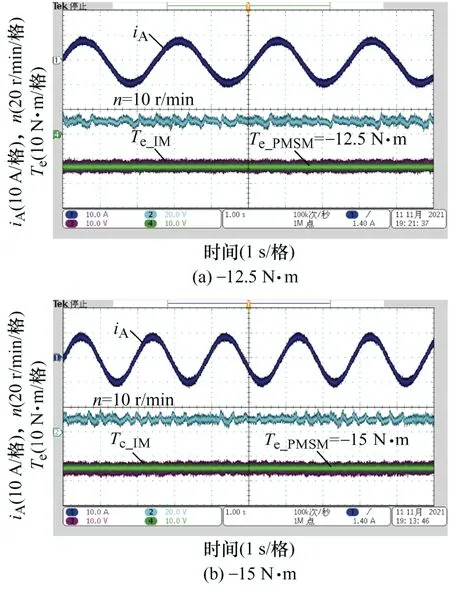
图9 反接制动转矩输出能力验证试验结果

由图9可知，IM转速均达到给定转速10 r/min。不同负载转矩下，IM输出制动转矩依次对应为-12.5 N·m、-15 N·m、-20 N·m和-22.5 N·m， 与负载转矩相平衡。不同负载转矩下依次对应的转差频率为-4.5 rad/s、-5.4 rad/s、-7.2 rad/s和-8.1 rad/s，定子角频率分别为-2.4 rad/s、-3.3 rad/s、-5.1 rad/s和-6.0 rad/s。由于定子角频率小于零，所以电机工作在反接制动状态。由试验结果得，IM在反接制动时可输出不同大小的制动转矩，且转矩平稳，从而验证了反接制动可以实现在低速区制动转矩的任意可控。

5.2 不同转速下电气制动转矩输出能力验证

为了测试不同转速下异步电机输出大转矩的能力，PMSM为IM提供-20 N·m的负载转矩，图10依次给出了转速为60 r/min、50 r/min、20 r/min和10 r/min时的试验波形。

由图10可知，IM均达到了给定转速并稳定运行；在不同转速下，IM制动转矩与负载转矩相平衡，IM的转差频率均为-7.2 rad/s，定子角频率分别为5.4 rad/s、3.3 rad/s、-3.0 rad/s和-5.1 rad/s，表明当转速为60 r/min和50 r/min时，IM工作在再生制动状态；当转速为20 r/min和10 r/min时，ωs小于零，IM工作在反接制动状态，且定子角频率的绝对值随转速降低而增大。

由图9、10可知，在不同转速及不同负载工况下，IM通过工作在再生制动及反接制动状态，实现了低速区制动转矩的稳定可控输出。

图10 不同转速下电气制动转矩输出能力验证试验结果

5.3 再生制动自然换向至反接制动验证

为了验证异步电机全电制动方式下的再生制动与反接制动的平滑过渡，逐渐降低IM的转速以实现再生制动至反接制动的自然换向。利用PMSM为IM提供-20 N·m的负载转矩，图11a给出了转速由60 r/min以10 (r/min)/s的减速度逐渐减速至5 r/min时IM的三相定子电流和转速，图11b给出了IM的三相定子电流和转矩。

首先，由图11a、11b三相定子电流相序可得，在制动减速过程中，定子电流相序发生了变化，说明IM实现了由再生制动至反接制动的切换。从定子频率的正负也可知，此减速过程包含再生制动和反接制动两个阶段。由图11c可知，34 r/min左右为定子频率过零点，即再生制动与反接制动间的切换点，所以当转速约为34 r/min时，再生制动结束，继续降低转速便会进入反接制动，仅通过再生制动无法实现制动至零速。同时，由图11a可知，正是在大约34 r/min时定子电流相序发生了变化。

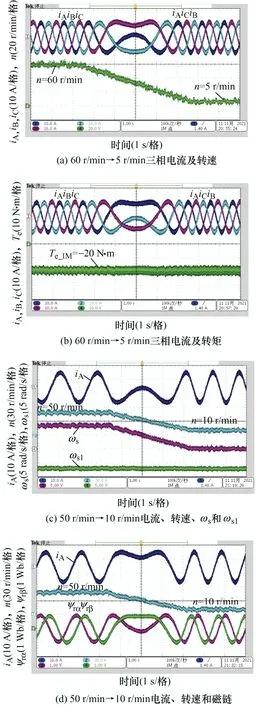
图11 再生制动自然换向至反接制动试验结果

图11c给出了间接矢量控制时IM的A相定子电流、转速、定子角频率和转差频率。由图11c可知，在整个制动减速阶段，转差频率始终保持为-7.2 rad/s，在再生制动与反接制动的切换点未发生电流冲击、转矩冲击或不稳定现象，整个制动减速过程，转矩平稳无冲击。

图11d给出了采用直接矢量控制时该制动减速过程中αβ坐标系下转子磁链的波形。从转子磁链α轴、β轴分量的相位来看，再生制动时，α轴分量超前β轴，而反接制动时，β轴分量超前α轴，正是由于转子磁场定向的改变，实现了再生制动向反接制动的切换。

以上试验结果表明，基于再生制动自然换向至反接制动的全电制动方式可以实现异步牵引电机低速区制动转矩的稳定可控输出，进而可以实现列车的全电制动。

6 结论

本文以异步牵引电机为研究对象，详细分析了一种基于再生制动和反接制动的列车牵引系统全电制动方式，旨在仅通过牵引电机的电气制动方式实现列车制动至零速。首先，从转差频率的角度分析了几种不同电气制动方式在低速区的转矩输出能力；其次，从转子磁场定向和磁链观测的角度分析了矢量控制下反接制动的实现原理；最后，确定了由再生制动自然换向至反接制动的全电制动方式，以实现低速区制动转矩的任意可控输出，进而满足列车不同减速度的制动需求。通过试验验证了该全电制动方式的可行性和有效性，并得出以下结论。

(1) 当ωs＜0时，异步电机进入反接制动方式，且制动转矩的大小完全可控。

(2) 当ωs＜0时，即反接制动工况下，基于转子磁场定向的矢量控制仍适用。

(3) 基于再生制动自然换向至反接制动的全电制动方式，可实现低速区制动转矩的稳定可控输出。