改进的共振稀疏分解方法及其在滚动轴承复合故障诊断中的应用
张守京 慎明俊 杨静雯 吴 芮
西安工程大学机电工程学院,西安,710600
0 引言
在长期、高速和重载等复杂条件下运行,轴承极易出现损伤。轴承中同时存在的多个缺陷引起的故障会导致多种故障共存,这些故障被称为复合故障[1]。轴承复合故障对旋转机械的危害很大,会导致设备性能加速下降[2]。由于多个共存故障产生的不同冲击信号相互干扰,并且弱故障冲击极易被强故障冲击淹没,使得复合故障信号特征的识别和提取变得极为困难[3-4],因此,复合故障特征分离与提取一直是滚动轴承故障诊断领域的难点所在。
滚动轴承复合故障冲击成分在时域中被噪声淹没,毫无规律可循;在频域中表现为各故障特征频率的相互耦合和干扰。在复合故障信号分解方面,SELESNICK[5]提出了信号共振稀疏分解(resonance-based sparse signal decomposition, RSSD)方法。不同于传统基于频率或尺度的信号分解方法,该方法依据品质因子Q的不同将复合信号分解为由持续振荡成分组成的高共振分量和由瞬态冲击组成的低共振分量。其中,瞬态冲击为宽带信号,其品质因子Q比持续振荡成分中的Q值小很多[6]。ZHANG等[7]将改进的变分模态分解作为RSSD分解的前置滤波器对信号进行处理,有效提取到轴承故障信息;何群等[8]将RSSD与最大相关峭度反卷积(maximum correlation kurtosis deconvolution, MCKD)相结合有效提取到滚动轴承的故障特征。以上分析中,对于RSSD的影响参数,如品质因子、分解层数的选择依靠人为经验,无法充分发挥RSSD信号分解的优势。
反卷积方法被认为是恢复周期性故障冲击的有效工具[9]。MCDONALD等[10]提出了多点最优最小熵反卷积(multipoint optimal minimum entropy deconvolution adjusted, MOMEDA)方法,通过引入目标向量和多点D范数来提供滤波器的非迭代最优解。与MCKD相比,MOMEDA无需提前确定故障周期并且可以处理非整数故障周期信号[11]。王靖岳等[12]利用小波降噪和MOMEDA方法成功提取出齿轮箱中的复合故障;XIANG等[13]结合MOMEDA和1.5维峭度谱提取到复合故障信号中轴承故障信息。
基于上述研究,笔者提出一种改进RSSD的滚动轴承复合故障诊断方法,该方法采用RSSD双参数优化技术以构造与不同故障特征匹配的最优小波基,通过子带重构以确定具有瞬态特征的最佳子带。改进后的RSSD具有自适应参数优化和筛选最佳子带捕获瞬态特征的能力,结合MOMEDA可识别并分离复合故障中各故障冲击。
1 基础理论
1.1 RSSD方法
RSSD[5]利用形态分量分析和可调品质因子小波变换(tunableQ-factor wavelet transform, TQWT)产生两个品质因子不同的过完备小波基,将含有高、低品质因子分量的复杂信号分解为高共振分量和低共振分量。其实现过程如下:
(1)TQWT通过双通道分解和合成滤波器组以迭代方式实现信号分解和重构。通过高、低通滤波器对前一个滤波器的低通输出进行迭代分解,得到J+1个子带的小波系数{W(1),…,W(J),W(J+1)}。图1为J层TQWT分解图。图中H0(ω)、H1(ω)为滤波器组的频率响应函数;w(J)为分解中产生的子带小波系数;β、α分别为高、低通尺度因子;r为冗余度。其计算式如下:

图1 J层TQWT分解图

(1)
(2)定义信号x由具有高振荡特性的谐波成分xH和具有低振荡特性的故障冲击xL组成。从x中分离出xH和xL的过程就转化为利用形态分量分析处理信号x时目标函数最小化问题:
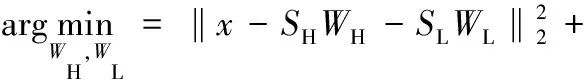
λ1‖WH‖1+λ2‖WL‖1
(2)
式中,SH、SL分别为由TQWT分解得到的xH、xL的过完备小波基;WH、WL分别为xH、xL的小波系数;λ1、λ2为正则化参数。

1.2 改进的RSSD方法
1.2.1RSSD参数选择与影响
RSSD的关键是生成两个分别与高、低共振分量匹配的过完备小波基,与小波基有关的参数有高、低品质因子QH、QL,高、低冗余度rH、rL和高、低分解层数JH、JL。冗余度影响小波振荡的程度,当rH=rL=3时,信号中高、低共振分量可以成功分离[14]。分解层数J影响RSSD分解速率,其大小受信号长度N的限制,具体如下:
(3)
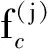
(4)
(5)
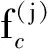
(6)
(7)
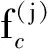
1.2.2RSSD双参数优化
由以上分析可知,必须合理选择高、低品质因子QH、QL及其分解层数JH、JL的值,方可确保分解后的子带频率能够覆盖各分量的共振频带,从而保证RSSD的分解效果。本文利用人工鱼群算法(artificial fish swarm algorithm, AFSA)实现RSSD双参数Q和J的自适应选取,构建一个复合指标作为目标函数,将RSSD参数QH、QL、JH、JL的范围定义为AFSA算法的搜索空间,实现RSSD双参数优化。
时域特征中峭度指标K体现了故障冲击的大小;频域中包络谱熵HES体现了故障冲击周期性强弱,HES值越小,表明故障冲击的周期性越明显。本文将K和HES相结合构建一个融合时频域特征的复合指标KES,表达式如下:
(8)
式中,p(xn)、pn分别为信号xn和其包络信号的概率密度。
KES值越大,表明信号中故障冲击越突出,周期性越强。将分解后低共振分量的KES作为AFSA算法寻优的目标函数,设定AFSA算法鱼群规模为20,迭代次数为30,搜索步长为0.5,拥挤因子为0.618,感知距离为0.5;结合1.2.1节的分析,设置高、低品质因子的寻优区间分别为3≤QH≤15,1≤QL<3,高、低分解层数的寻优区间为1≤JH≤Jmax,1≤JL≤Jmax。
1.2.3子带重构
以上分析已实现RSSD双参数QH、QL,JH、JL的自适应选取,利用参数优化后的RSSD可获得最优低共振分量及对应的J+1个子带。为了最大限度地提取信号中的瞬态冲击,提出一种新的子带筛选准则——利用周期性故障冲击的能量分布特性作为最佳子带的筛选标准,以获得有效故障信息频段。子带j处的能量Ej表示为
(9)

计算子带j在J+1个子带能量中的占比ej,选择能量占比在10%以上的子带为最佳子带jopt,即
(10)
(11)
最后将筛选出的最佳子带jopt进行重构,再进行后续分析。
经以上分析,改进后的RSSD可成功捕获复合故障信号中的瞬态冲击成分。识别并提取各故障诱发的单一脉冲信号可看作是一个反卷积过程。因此,可进一步利用MOMEDA对周期性故障冲击的敏感性,自动确定脉冲信号的数量及其周期。
1.3 MOMEDA方法
MOMEDA以非迭代的方式来找到最佳滤波器f,并将输入信号x恢复至原始冲击信号y[16]。反卷积过程如下:
(12)
式中,L为滤波器长度。
通过引入多点D范数(multi d-norm, MDN)并求其最大值来获得最优滤波器,过程如下:
(13)
式中,T为故障周期;t为确定脉冲位置和权重的目标向量。
在处理复合故障信号时,引入多点峭度(multipoint kurtosis, MKurt)来确定各故障冲击的位置:
(14)
当目标向量t的长度等于故障周期T时,MKurt谱中会有明显的谱峰[17];利用谱峰对应的周期对信号进行MOMEDA处理,可得到故障冲击。
2 改进RSSD滚动轴承复合故障诊断方法
轴承故障瞬态冲击信号非常微弱,很难从复合故障信号中提取单个缺陷诱发的故障特征,因此,提出了基于双参数优化、子带重构改进的RSSD与MOMEDA结合的复合故障诊断方法。改进后的RSSD能有效分离复合故障信号中瞬态冲击信号和持续振荡的谐波信号,实现初步降噪。然而,RSSD分解得到的低共振分量子带重构信号中,与各个故障相关的周期性脉冲信号仍存在耦合现象,并且噪声并没有完全消除。针对此,运用MOMEDA对与不同故障类型相关的周期性脉冲信号进行解卷积处理。本文方法流程如图2所示。具体步骤如下:

图2 本文方法流程示意图
(1)RSSD双参数优化。通过构建融合时频特征的指标KES作为目标函数,采用人工鱼群算法自适应选择RSSD最优高、低品质因子和分解层数,获得包含故障冲击的最优低共振分量。
(2)子带筛选与重构。依据所提出的子带能量筛选原则选择最佳子带jopt,并对其进行重构。
(3)MOMEDA特征提取及包络谱分析。利用多点峭度谱识别各瞬态脉冲的故障周期;运用MOMEDA进行提取各个故障特征并对其进包络谱分析,实现复合故障检测。
3 仿真分析
建立以下复合故障仿真信号来验证本文方法的可靠性:

(15)
式中,x(t)、y(t)分别为内圈、外圈周期性故障冲击信号;A0为振幅,A0=0.5;fr为转频,fr=30 Hz;C1、C2为衰减系数,C1=500,C2=400;fn1、fn2为共振频率,fn1=3000 Hz,fn2=2000 Hz;B(t)为干扰谐波,B(t)中的频率f1、f2分别取75 Hz和55 Hz;Ti为内圈故障周期,Ti=1/fi,fi为内圈故障特征频率,fi=160 Hz;To为外圈故障周期,To=1/fo,fo为外圈故障特征频率,fo=70 Hz;n(t)为加入信噪比为-10 dB的白噪声。
采样频率为16 000 Hz,分析点数为8192个。仿真信号时域及谱分析如图3所示。图3a中红色和粉色部分的内圈、外圈冲击信号被完全淹没在噪声中,时域信号毫无规律可循;频谱图中激起了两个共振频带;包络谱中故障频率并不明显,传统的谱分析法失效。

(a)时域波形
采用本文方法进一步处理仿真信号。执行AFSA搜索得到QH=5.35,QL=1.16,JH=29,JL=13。设定RSSD参数对信号进行分解,结果如图4所示,最优高共振分量中主要包含谐波成分;最优低共振分量中冲击特征明显,主要包含缺陷诱发的瞬态冲击。相比于原始信号,不仅提取了冲击特征,又进行了初步降噪。

(a)最优高共振分量
图5给出了最优低共振分量子带能量图。子带5、6、11、12的能量占比(图5中右侧数据)较大,符合所提出的子带筛选准则。图6所示为子带重构信号时域波形及包络谱。与图4b相比,重构信号时域图中干扰噪声明显减少并且故障冲击特征更加明显,其包络谱中可观察到幅值为(fi-fo)的频率成分及其倍频,初步判断轴承内外圈出现故障。但由于各故障间的耦合作用和噪声干扰,主故障无法确定,还需对信号进一步处理。

图5 低共振分量子带能量图

(a)子带重构信号时域波形
图7所示为子带重构信号MOMEDA处理结果,图7a所示为子带重构信号多点峭度谱,在周期Ti=100及其0.25倍、0.75、2倍处呈现较为明显的峰值,且周期To=228.57及其0.15倍处的谱线也较为突出。对重构信号运用MOMEDA算法处理时,设定周期区间的长度时需要将不同的故障周期包含在不同的区间范围内。因此,本文设定周期区间长度为10,分别设置反卷积周期区间为[95,105]和[224,234],结果如图7b~图7e所示。图7b和图7d时域波形中周期性故障冲击明显增强且呈现出一定的等间隔规律;对应包络谱中内圈故障特征频率fi、外圈故障特征频率fo及倍频成分清晰可见,验证了本文方法在复合故障诊断方面的有效性。

(a)子带重构信号多点峭度谱
4 试验分析
试验数据取自雷亚国教授课题组发布的XJTU-SY轴承全寿命周期数据集[18]。轴承全寿命周期加速试验台如图8所示,试验轴承型号为LDK UER204,具体参数如表1所示。通过调节待测轴承水平方向、垂直方向上的径向力大小和交流电机的转速获得轴承全寿命周期故障信号。试验设置采样频率fs为25.6 kHz,选择分析的数据长度为8192点。表2给出了不同转速条件下轴承内圈、外圈和滚动体的故障特征频率。

图8 轴承全寿命周期试验台

表1 LDK UER204轴承参数

表2 不同转速和载荷下轴承各部件故障特征频率
4.1 内圈和外圈复合故障
电机转速为2100 r/min时得到轴承内圈、外圈复合故障信号时域图和包络谱如图9所示。受强噪声的影响,时域中无法观察到周期性的故障冲击脉冲,其包络谱中受干扰谱线影响较为严重,没有提取到有效特征信息,即传统谱分析法失效。

(a)时域波形
采用本文方法进行分析。首先以低共振分量的KES为目标函数执行AFSA搜索,得到QH=4.92,QL=1.03,JH=31,JL=9。图10所示为参数优化后RSSD分解结果,图10a最优低共振分量信号中的故障冲击成分较为突出;将子带能量图中子带4、5、6、7进行重构,并对其进行包络解调,如图10c所示,可以观察到特征频率为n(fi-fo)(n=2,3,4,5,7)的成分,但无法确定故障源,需对信号作进一步处理。

(a)最优低共振分量
图11所示为MOMEDA处理结果。图11a子带重构信号多点峭度谱中,在周期Ti=140.8与To=237.24及其倍数处呈现较为突出的谱线。将子带重构信号在[135,145]和[232,242]两个周期范围内运用MOMEDA进行反卷积处理,结果如图11b~图11e所示。由图11b和图11d可看出,MOMEDA明显增强了内圈、外圈故障信号的周期性故障冲击;包络谱中内圈、外圈故障特征频率及其倍频处谱线较为突出。由此确定轴承内圈、外圈出现故障,与实验结果一致。

(a)子带重构信号多点峭度谱
采用文献[8]中提出的RSSD-MCKD方法进行对比分析,提取内圈、外圈故障特征时分别设置MCKD滤波器长度和反卷积周期分别为[396,148]、[310, 237],结果如图12所示。受干扰谱线的影响,内圈和外圈故障特征率成分并不明显,效果不佳。

(a)MCKD滤波后内圈故障包络谱
4.2 内圈、外圈和滚动体复合故障
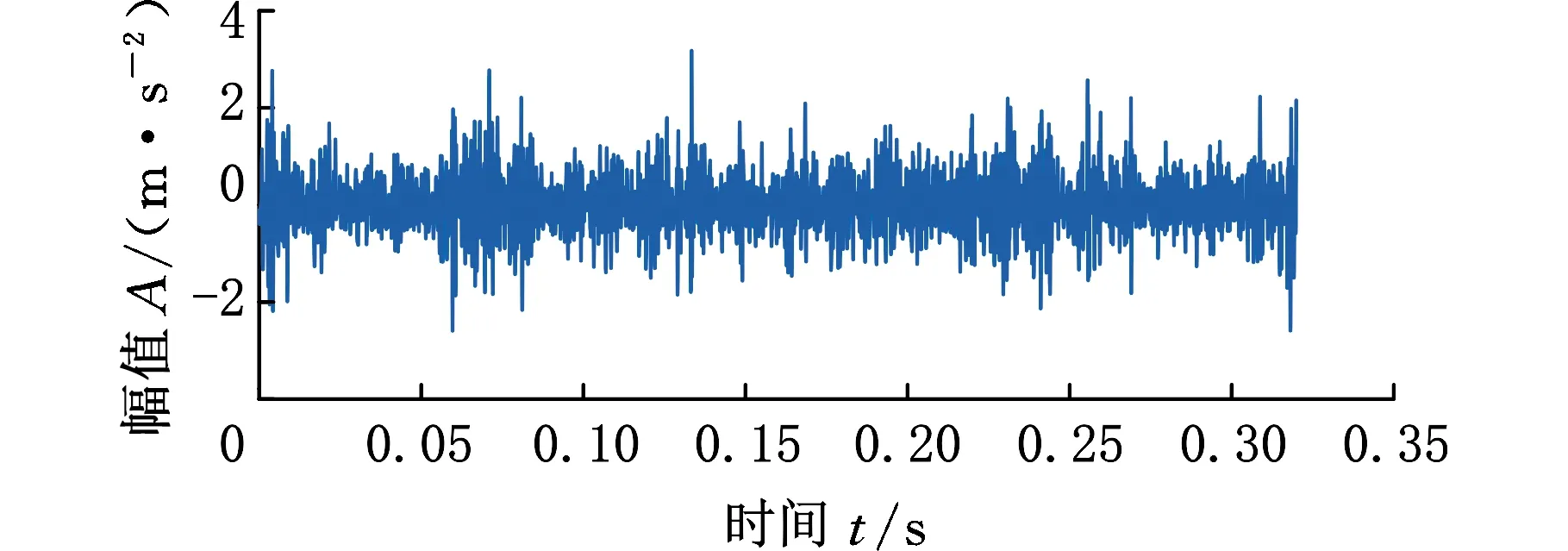
图13所示为电机转速为2400 r/min时轴承三种复合故障信号的时域波形,受噪声干扰较为严重,无法分辨故障冲击成分。

图13 三种复合故障信号时域波形
利用改进的RSSD方法对三种复合故障信号作进一步处理。执行AFSA寻优得到结果为QH=5.83,QL=1.12,JH=27,JL=11。图14为参数优化后的RSSD分解得到的最优低共振分量及其子带能量图,与原始信号相比,图14a中瞬态冲击成分较为明显;将最优低共振分量子带能量占比图中子带4、5、6进行重构,对其进行MOMEDA处理,结果如图15所示。
(a)最优低共振分量
从图15a中可以看到在故障周期Ti=128.6、To=204.8与Tb=296.6及其倍数处的峰值突出;将子带重构信号在[123,133]、[199,209]和[292,302]三个周期区间内运用MOMEDA处理,结果如图15b~图15g所示。图15b、图15d与图15f时域中内圈、外圈和滚动体的周期性故障冲击被MOMEDA明显增强;对应的包络谱中,内圈、外圈和滚动体的故障特征频率及其倍频成分清晰可见。

(a)子带重构信号多点峭度谱
图16所示为采用对比方法RSSD-MCKD的分析结果,分别设置MCKD滤波器长度和反卷积周期分别为[375,128]、[267, 205]和[242,296]。由于干扰谱线幅值过高,故内圈、外圈和滚动体特征频率成分并不清晰。

(a)MCKD滤波后内圈故障包络谱
5 结论
针对滚动轴承复合故障信号中各故障冲击特征受传输路径和其他干扰源的影响难提取的问题,提出一种双参数优化、子带重构改进的共振稀疏分解(RSSD)方法。与传统的RSSD方法不同,品质因子和分解层数的优化提高了RSSD的分解性能,对得到的最优低共振分量进行子带筛选与重构,能最大限度地保留有效故障信息;利用MOMEDA对周期性故障冲击的敏感特性可自适应地确定冲击信号的数量及其周期。仿真分析和两种不同类型的复合故障试验研究表明,与传统的共振稀疏分解与最大相关峭度解卷积(MCKD)结合的方法相比,本文方法能精确实现轴承复合故障诊断。

