一种用于鸭翼控制的摇头型双圆环压电马达研究

刘吉磊 陈 超 陈 恒 王均山 吴树熊

南京航空航天大学机械结构力学及控制国家重点实验室，南京，210016

0 引言

压电马达是一种基于逆压电效应来实现电能转换到机械能的微特驱动执行器[1-4]，具有直接输出低速大力矩、快速响应、断电自锁、结构简单等特点，在特定领域展现了良好的应用前景。压电马达利用结构丰富的振动模态来工作[5]，可针对具体应用环境充分创意构思提出不同形式的原理性方案[6-10]。其中，摇头型压电马达具有易微型化、快速响应、安静的特点，成功地集成用于自动聚焦镜头中，符合高端光学调焦系统结构精巧、安静且快速对焦的趋势和要求，成为压电马达历史上成功的一次应用[11-13]。正是将压电马达的独特优点恰当地应用于特定领域，造就了如今仍然广泛使用的基于压电马达的高端单反镜头品牌。在此背景下，国内外研究机构为扩展应用领域，持续聚焦不同类型和不同特点压电马达的研究[14-15]。

清华大学研制出成系列的杆式压电马达样机[16-18]，其中包括直径为1 mm的微型杆式压电马达，初步开展了压电马达在医学内窥镜以及微精密驱动平台领域的应用探索。哈尔滨工业大学提出了一种半径2 mm的半圆半方型弯曲行波压电马达[19]，具有结构简单和紧凑的优点。南京航空航天大学研究了系列圆周体压电马达[20-23], 开展了运动机理和样机试验工作。以上研制的系列压电马达充分研究了杆式压电马达的运动机理，为进一步面向应用的开发奠定了基础。

压电马达具有结构简单紧凑、低速大力矩和快速响应的特点，需要充分挖掘创新的构型来适应背景应用[24]。压电马达在结构设计上具有很大的灵活性，容易与传动系统集成设计，适用于对执行器系统的体积、质量和集成度有较高要求的制导弹药控制系统中[25]。

本文针对制导弹药平台对舵机的紧凑、直驱和断电自锁等要求，提出了一种采用夹心式换能器诱发两端圆环面外弯曲振动的复合型压电定子结构，由此可构成结构精巧的摇头型双圆环(双)输出轴旋转压电马达(以下简称双圆环压电马达)，用以驱动鸭式舵翼产生偏转运动从而形成可变攻角。通过开展基于该夹心式换能器的双圆环形定子结构动力学设计和分析，搭建了测试平台，对试制样机的输出特性进行了实验研究。

1 应用于鸭舵驱动的双圆环压电马达结构设计

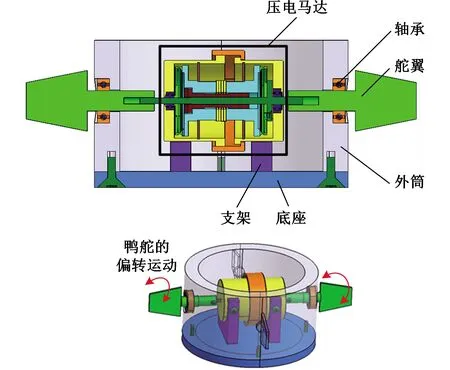
图1 用于鸭舵驱动的双圆环(双)输出轴压电马达

图1中的底座与制导弹药本体连接，夹心式双圆环压电马达通过两个支架固定在底座上。马达两端输出轴与翼片相连接，按照控制指令驱动鸭式翼片的运动，为制导弹药的轨迹控制提供所需的气动操纵力。

双圆环(双)输出轴旋转压电马达结构如图2所示：压电马达定子的主体为夹心式换能器，在换能器的两端设计有用于放大振幅的圆环形结构；将两端输出轴上的转子分别以一定预压力安装于两端环形定子齿面上，利用支架将定子固定在罩体内部，其中转子输出轴可以直接连接需要驱动的舵翼片(图1)；采用一紧固螺母将两壳体进行连接，通过改变旋紧螺母的位置来调整定子、转子之间的预紧力。摩擦材料分别粘贴于两片转子的驱动面上，用于提高定子与转子之间的驱动和摩擦效果，改善压电马达的输出特性和工作稳定性。

上述双圆环(双)输出轴压电马达利用夹心式换能器的摇头运动，激发出两端圆环形定子的工作模态，从而驱动双转子旋转。显然，该型压电马达为对称结构，主要由定子、转子、轴、外罩壳和外螺母几部分组成。压电马达的定子主体为一个兰杰文换能器，换能器两端分别设置有用于驱动转子的定子环，每个定子环通过4个支撑杆与兰杰文换能器相连接。如图2所示，通过螺栓将上定子部件、下定子部件、电极片和压电陶瓷紧固为一个整体。通过给压电陶瓷施加特定的激励电压，可使夹心式换能器产生空间正交、时间相位差π/2的两个弯曲振动，两者叠加成摇头运动，从而诱发两端圆环表面产生行波，在定子齿面产生椭圆运动驱动转子旋转，同时带动与之相连接的输出轴旋转，进而实现舵翼的偏转运动。

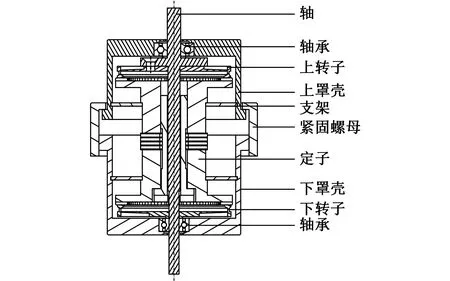
图2 压电马达定子的结构示意图

2 双圆环压电马达的驱动机理

夹心式换能器采用基于d33效应的两分区弯振压电陶瓷片，定子中的压电元件分为两组，如图3中的A相和B相。两组弯振陶瓷片的极化区空间位置交错放置(彼此相隔π/2)，若在两组压电元件中施加相位差π/2的激励电压，可在夹心式圆柱型换能器中激发出相位差π/2的空间正交弯振模态并合成摇头运动，通过换能器两端的支撑杆激励圆环的振动，最终能在圆柱型换能器两端的圆环形驱动面产生行波和椭圆运动。

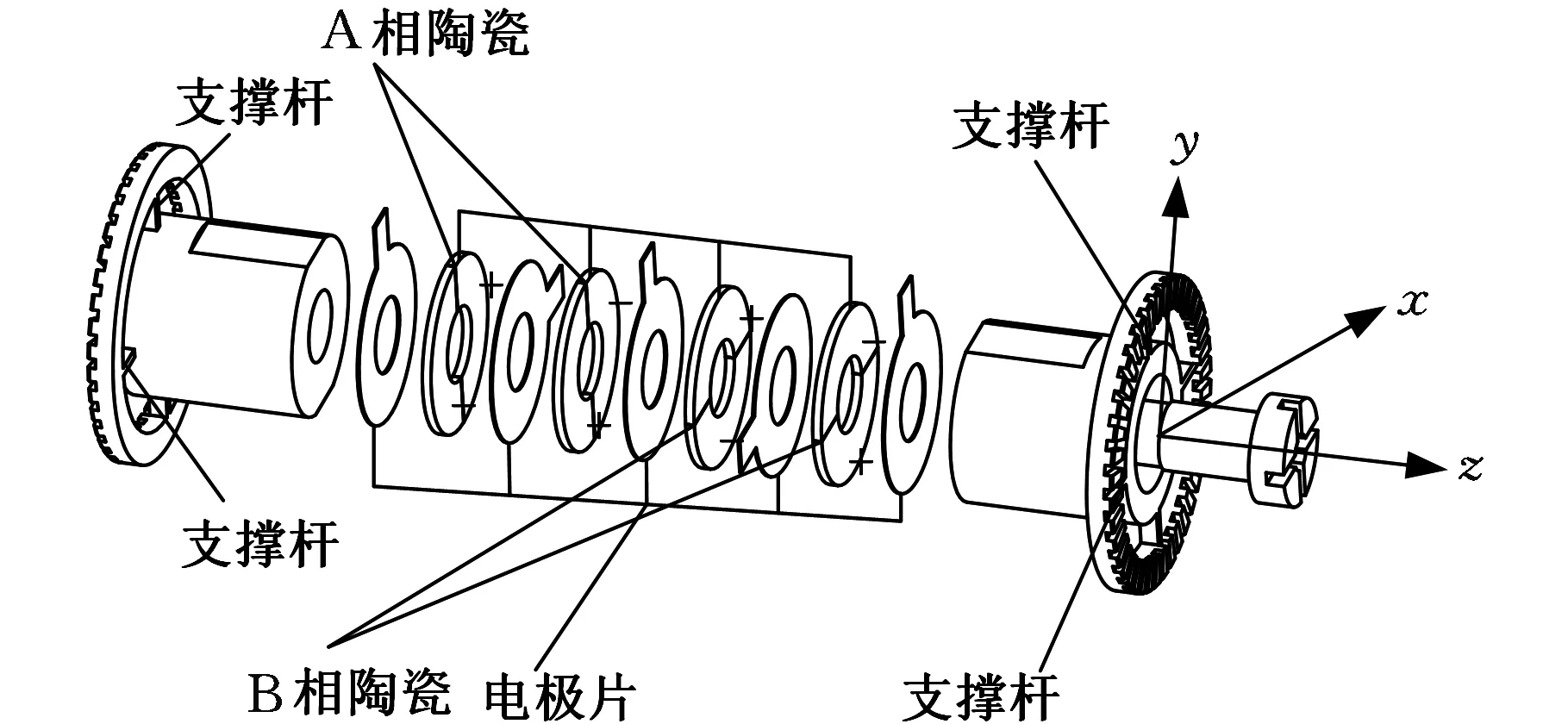
图3 定子压电激励单元的布置

复合型压电定子中的圆柱型夹心式换能器选用一阶弯振模态，固定于换能器两端的圆环选用零节圆、5节径的B05面外弯曲模态。当施加适当的激励电压时，通过A、B两组压电元件激发出圆柱型换能器的A、B两相一阶弯振模态(图4)，在换能器的两端合成为摇头运动，通过支撑杆传递能量并激发圆环的五阶弯振模态，最后在两端的圆环上产生行波，通过摩擦力驱动转子旋转。其中，压电马达的旋转方向可由两相交流电压的相位差确定。

(a)A相模态 (b)B相模态

双圆环压电马达复合定子的两端圆环为对称结构，对复合定子其中一端的驱动面运动方式进行分析。因为圆柱型梁的定子的振动是微米级的，所以无论是它的弯振还是纵振，均可假设定子驱动端面在振动过程中不产生形变，即其运动为刚体运动。

图5为定子驱动端面及振动变形示意图，其中，o为驱动点所在圆周的圆心，P0为一个特定的驱动点，用角度α来表示任一驱动点P的位置。假设陶瓷组A激发的A相弯振模态在oxz平面内，陶瓷组B激发的B相弯振模态在oyz平面内。A相弯振变形时，在oxz平面内，定子端面相当于沿x轴平移W0的同时又转过了一个角度β0。B相弯振与之类似。纵振则是定子端面以oxy平面为平衡位置，沿z轴做往复运动。

狗娃不知从哪里搬回来两个巴掌厚的大方石，又向他父亲要来打磨盘的锉刀和榔头，乒乒乓乓敲打起来。折腾了半个月，狗娃终于凿成了一对石锁。他一只手拧起一个，掂了掂，十分地骄傲。打这以后，狗娃每天天不亮提着两个石锁往山上跑，风雨无阻。练了个把月，说是石锁轻了，又给腿上绑了沙袋继续跑。

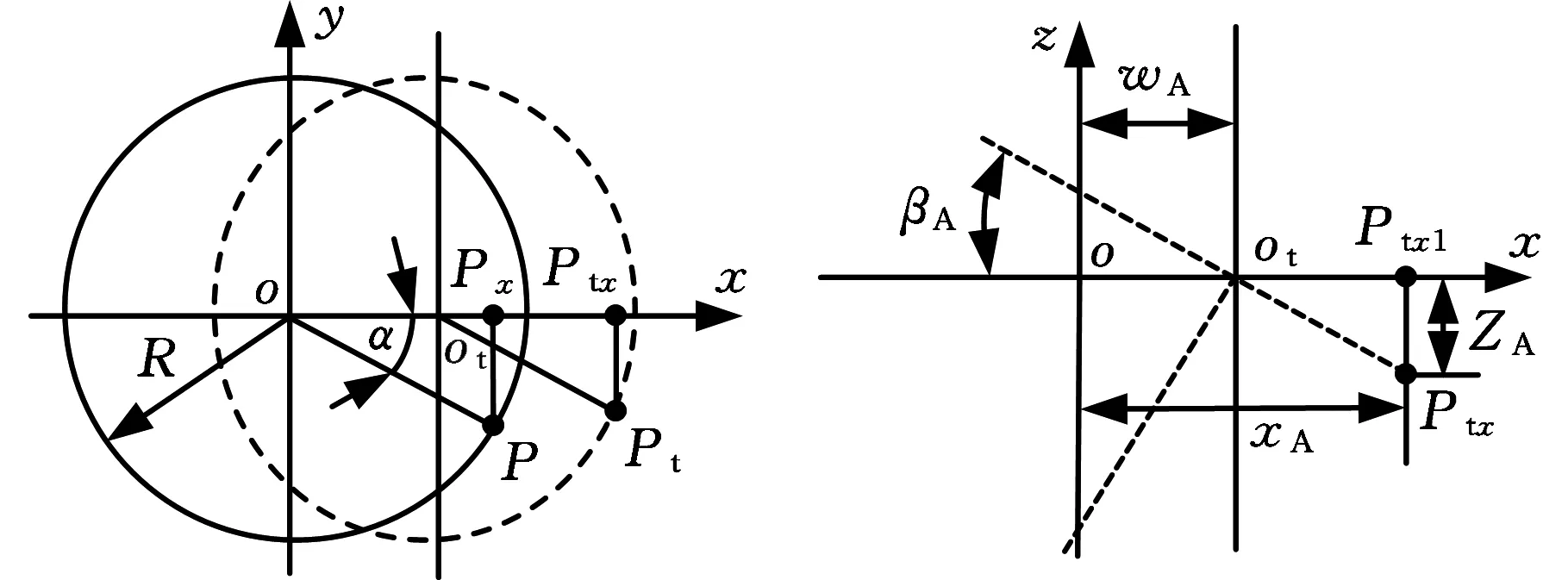
图5 定子端面变形示意图

以圆柱式换能器对称轴为z轴建立圆柱坐标系(参见图3)，x轴沿弯振方向，y轴则按右手准则确定。不失一般性，选取一组陶瓷A在简谐激励下的振动响应：假设在t时刻，O点在x方向产生位移wA，同时端面的旋转位移为βA，则可表示为

(1)

其中，ω为振动圆频率。圆柱式换能器端面某一驱动点P在oxz坐标系中的坐标可表示为

(2)

其中，R为头部的圆环半径。将式(1)代入，并考虑到βA很小，式(2)可近似写成

(3)

同理，另一组陶瓷B也可以激发出类似形式振动响应：

(4)

因此，当A、B两相弯振合成时，根据式(3)和式(4)，驱动点P在oxyz坐标系中运动轨迹的参数方程可表示为

(5)

由式(5)可知，圆柱形换能器的端面沿z向位移表现为行波，半径越大，对位移响应的放大效果就越明显。因此，提出双圆环(双)输出轴的思路，即通过图4中支撑杆放大端面的振幅输出。但在实际设计过程中，支撑杆并非越大越好，需要考虑阻尼和干扰模态的影响。

当圆柱形换能器产生摇头运动时，其端面的圆环在支撑杆的激励下就有可能被激发出面外的弯曲振动，这将通过以下复合型定子的结构动力学设计来保证。

3 复合型定子的结构动力学仿真与设计

对于双圆环压电马达工作模态的选择，原则上必须使圆柱式换能器与两端圆环的频率一致[18-20]。为了使定子得到有效的激励，将圆柱型换能器第一弯曲模态的固有频率设计为等于圆环结构的第五阶弯曲模态频率(即圆周有5个波)。根据上述设计原则，在商用有限元软件中建立了复合型定子的参数化数值计算模型(图6)，经过迭代计算和尺寸调整，最终确定了定子外形尺寸(表1)。其中，D1为圆盘外径、D2为圆盘齿的内径、D3为圆柱段直径、L1为圆柱段长度、L2为圆盘厚度、L3为齿槽深度、T为圆盘支撑杆的宽度，两端面每个圆环的齿数为40，第五阶弯曲模态频率约为27 kHz。

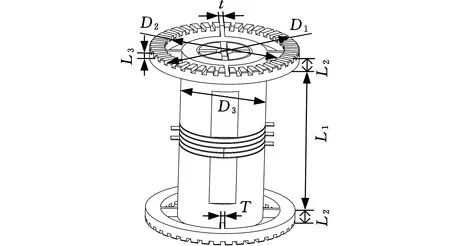
图6 定子整体尺寸参数

表1 定子结构尺寸

选定表1的参数后，对整个复合型定子在27 kHz激励下的振动响应进行谐响应分析，如图7所示，其中斜椭圆S为圆环上任意一点的空间轨迹。结果表明双圆环压电马达的复合定子能够在该频率下同时激发出圆柱型换能器一阶弯振和圆环五阶弯振模态。

图7 复合定子的谐振响应

选取定子驱动面上一点的运动轨迹进行瞬态运动学仿真：给陶瓷A和B分别施加频率为27 kHz、幅值为100 V的交流电压。选取结构达到稳态的最后一个振动周期时，该点的运动路径如图8中所示的S，其中粗黑线椭圆是选取点的路径，其他椭圆是该点在xy、xz和yz平面上的投影。结果表明，该点具有轴向、切向和径向振动位移，空间运动轨迹为一斜椭圆。

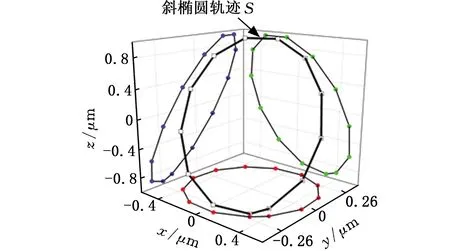
图8 复合定子圆环上点的椭圆运动轨迹

4 样机的实验研究

4.1 复合型定子的模态实验

基于上述原理和结构动力学设计后，最后加工的样机如图9所示。采用多普勒激光测振系统(PSV-300F-B)对马达的复合定子振动特性进行了测试，给压电陶瓷施加幅值为100 V的驱动电压时，分别选取圆柱兰杰文换能器的母线和圆环表面作为测试对象，其幅频特性的关系分别如图10所示。可以看出，当施加100 V的驱动电压时，圆柱式换能器的一阶弯振频率约为26.72 kHz，而圆环的共振频率为26.87 kHz，一致性很好，微小的差别来自加工和材质等因素。因此，后续的定频扫描和整机测试时均采用26.87 kHz的激励频率。

图9 双圆环压电马达样机

(a)换能器

图11为换能器和圆环面外振动的定频测量图(激励频率26.87 kHz、驱动电压幅值为100 V)，得到了复合定子的振幅响应和直观的振型。可以看到，在上述激励条件下，圆柱式换能器的确被激发出了一阶弯振模态，端面的圆环被诱发出5个波长的振动模态，并且在圆环驱动面的振幅可达到1.5 μm。实际测试结果与前述基于有限元法的结构动力学设计和仿真结果吻合。

(a)换能器 (b)端面圆环

4.2 双圆环压电马达样机输出特性实验

装配马达样机时，适宜的预压力有利于接触面产生稳定的摩擦作用，将定子的微幅振动转换为转子的旋转。如图3所示，采用调节外螺母的旋入深度，实现施加预压力的效果。力传递过程可以概括为调节螺母的旋入深度，通过罩壳、轴承、转子的依次传递，最终达到定子和转子接触面。

搭建了图12所示的测试平台对双圆环压电马达样机的输出特性进行实验测试：利用功率放大器(HFVA-83A，南京佛能)将信号发生器(AFG3022B，泰克)中两路输出电信号进行放大，用于给马达复合型定子施加特定频率和幅值的电压；在压电马达输出轴端设置有标志，通对激光位移传感器(LK-G30，基恩士)读取到标志位置的脉冲信号，可以判断马达位移的旋转圈数，处理后得到马达的实际转速。

图12 输出特性测量系统及马达原理样机

马达样机的定子和转子之间的预压力为40 N，电压峰峰值为250 V和300 V时的激励频率与空载转速的关系如图13所示。可以看出，当激励电压频率在定子共振频率点附近时，马达输出转速达到最高，分别为150 r/min(250 V时)与190 r/min(300 V时)，压电马达顺时针旋转效果比逆时针要好，这主要是由于实际的加工精度和装配等因素影响马达的结构对称性，从而引起两个方向的驱动效果不一致。

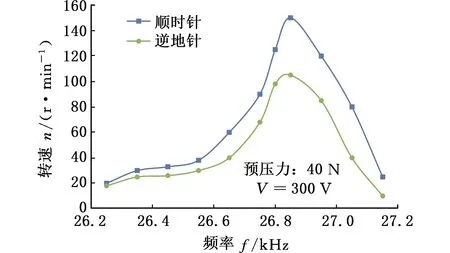
(a)250 V

利用悬挂重物的方式对马达的力矩输出特性进行测试，结果如图14所示。可以看出，当给压电陶瓷施加频率为27 kHz，幅值分别为250 V、300 V和350 V的电压激励时，马达输出的转速随着输出力矩的增大而减小。在相同的负载力矩作用下，压电马达的转速随着激励电压的升高而增加。但是在实际应用过程中，电压过高容易导致压电陶瓷被击穿，从而大大缩短压电马达的使用寿命。因此，本文提出的双圆环压电马达提出工作电压不应超过350 V。

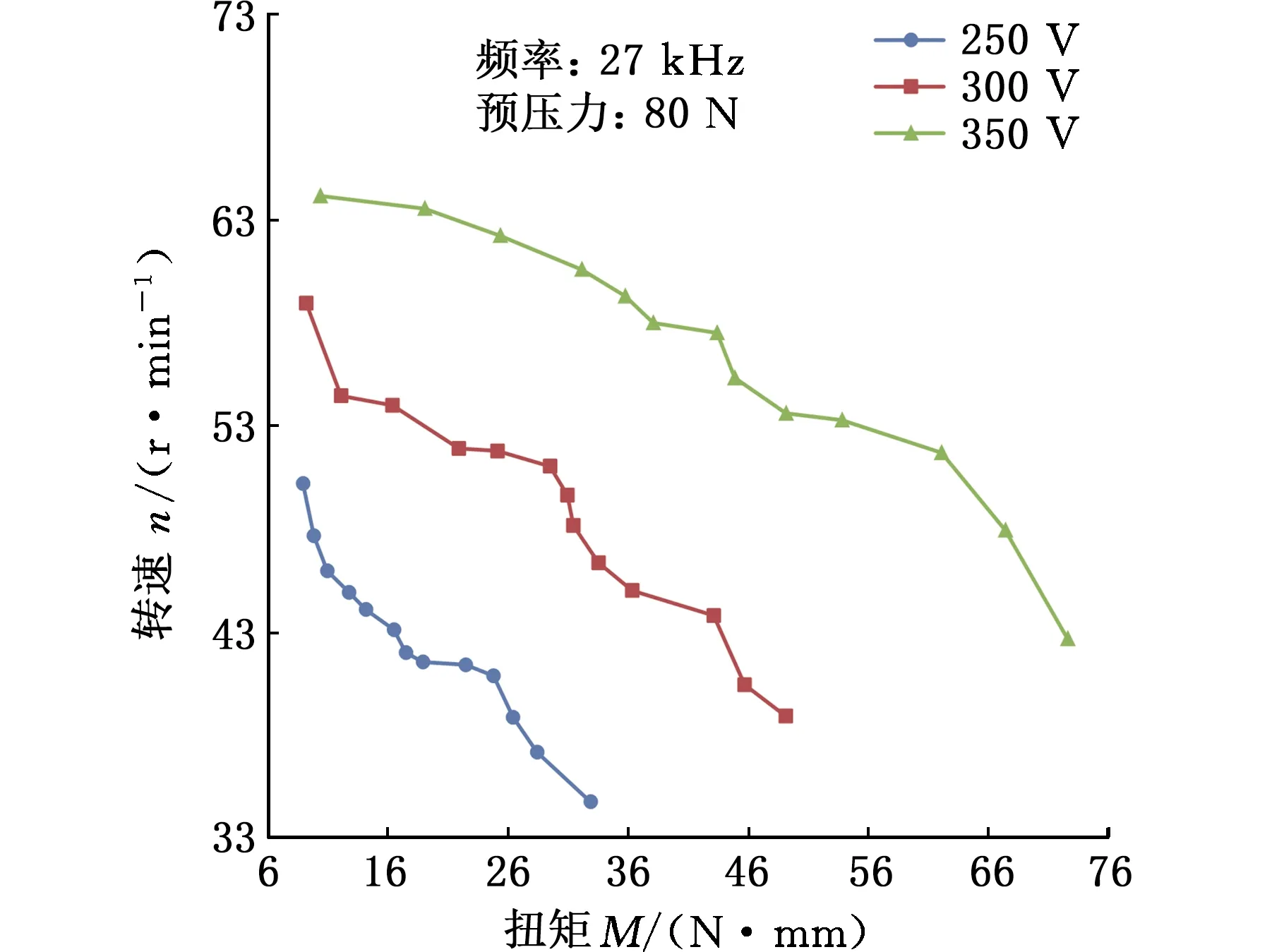
(a)顺时针

5 结语

实验结果表明，当驱动电压为300 V的情况下，样机的堵转力矩不低于0.04 N·m，最大转速约为190 r/min，满足某平台微驱动舵机工作时的应用需求。由于加工精度和装配等问题，样机两输出端存在输出不一致的现象。下一步研究将继续对该型方案的结构进行优化(如提高定子的振幅输出、夹持方式和位置的选择)，该型压电马达的输出性能还可进一步提高。