工件分特征下的五轴数控机床关键几何误差分析与补偿方法
卢成伟 钱博增 王慧敏 项四通
宁波大学机械工程与力学学院,宁波,315211
0 引言
五轴数控机床灵活性好、生产效率高,在制造业中发挥着重要作用,广泛应用于汽车制造、航空航天等领域。几何误差是数控机床在制造与装配过程中引起的不可避免的偏差,严重影响机床的加工精度,但具有重复性好、长时间内稳定的特点[1],故补偿几何误差已成为较为实用与可行的提高机床整体加工精度的方法之一。然而五轴机床的几何误差多达41项[2],补偿所有的几何误差工作量大,因此辨识并补偿影响机床加工精度的关键几何误差具有重要意义。
灵敏度分析可有效地确定输入参数变化对输出结果影响的关键性[3],该方法已成为量化几何误差对机床加工精度的影响和辨识关键误差的有效途径。常见的灵敏度分析方法可分为局部灵敏度分析和全局灵敏度分析两种[4]。局部灵敏度分析亦称“一次变化法”,此种方法仅检验一个参数,其他参数取中心值,评价输出结果在该参数变化时的变化量,如偏微分运算法[5-7]。全局灵敏度分析检验多个参数同时变化及参数之间的相互作用对输出结果的影响,其结果受多个输入参数的影响,常见方法有Sobol法[8]、Morris法[9]和积分法[10]等。
近些年来,国内外学者基于灵敏度分析方法对机床几何误差展开了大量研究。LI等[11]考虑刀具的位置和姿态,分别使用全局和局部灵敏度对BC双摆头五轴机床进行了分析,研究发现几何误差中的角度误差对机床加工精度的影响较大。刘奕颖等[12]以机床装配阶段中的几何误差为出发点,基于灵敏度分析方法对精密卧式镗床的运动轴进行公差设计。GUO等[13]引入全局定量灵敏度分析,充分考虑机床工作空间几何误差的概率分布,直观地描述了几何误差分量对位置和方向误差矢量的影响,确定了各几何误差对机床精度的影响。FU等[14]发现不同轴对机床精度的影响因其在机床结构中的位置及其局部误差而异,提出了机床各运动轴的几何误差贡献建模和灵敏度评估方法,获得了各轴的几何误差对机床加工精度的影响,并确定了机床的关键运动轴。ZHANG等[15]基于Sobol法与遗传算法对三轴立式铣床的全局灵敏度进行了分析,并采用乘法降维法来简化计算。杨赟等[16]基于灵敏度分析得出的关键几何误差,提出了一种批量化建模和补偿方法,对一批相同类型的三轴立式加工中心进行了批量误差补偿,提高了机床精度。上述研究在灵敏度分析中虽然取得了一定的成果,但大多数研究主要关注几何误差对机床体积误差的敏感性,而对工件形状误差的敏感性讨论较少。
面向复杂工件的形状误差,学者们亦开展了灵敏度分析研究。LI等[17]使用灵敏度分析方法确定了轨迹对误差运动的敏感性,并通过加工ISO 10791-7-M3试件及S形试件进行了验证。XIA等[18]建立了几何误差与齿面位姿误差之间的映射模型,基于全局灵敏度分析确定了影响齿廓和螺旋偏差的关键几何误差,从而简化了误差补偿表达式并提高了齿轮加工精度。YAO等[19]建立了考虑几何误差的超精密金刚石车削中心的运动学误差模型,通过灵敏度分析得出了影响加工精度的关键误差,并提出了一种减小或消除相应机械系统定位误差的对准方法,从而提高了被加工曲面的成形精度。上述研究通过灵敏度分析确定了影响工件整体加工精度的关键几何误差。然而五轴加工中,复杂工件通常由多个典型特征组成,且各特征受几何误差的影响程度不同,因此对工件整体进行灵敏度分析的效果不如分特征分析。
针对上述问题,本文提出了一种工件分特征下的五轴数控机床关键几何误差分析与补偿方法。将工件特征分解为平面、斜面、圆柱和圆锥台等典型特征,基于灵敏度分析分别辨识出各典型特征对应的关键几何误差。最后,通过对辨识出的关键几何误差进行补偿,有效地提高了工件的加工精度。
1 误差模型的建立
1.1 机床的体积误差模型
图1a为AC双转台五轴机床的结构示意图,该机床包含X/Y/Z三个平动轴以及A/C两个旋转轴。本文依据多体系统理论和齐次坐标变换建立了机床的体积误差模型。该机床的运动链为WCAMXYZT型,具有图1b所示的运动链结构与连接关系。A轴和C轴属于工件运动链,X轴、Y轴和Z轴属于刀具运动链,运动链遵循“WCS→CCS→ACS→MCS→XCS→YCS→ZCS→SCS→TCS”的传递顺序。其中,WCS表示工件坐标系,ACS、CCS、XCS、YCS、ZCS分别表示A轴、C轴、X轴、Y轴和Z轴的坐标系,MCS表示机床坐标系,SCS表示主轴坐标系,TCS表示刀具坐标系。
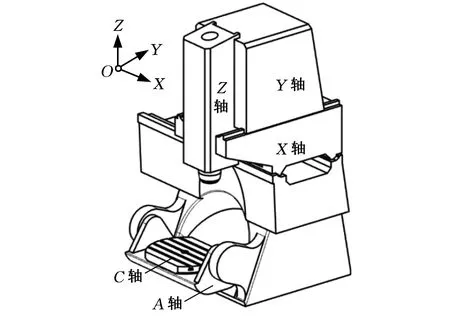
(a)AC双转台五轴机床结构示意图
在该机床运动链链中,主要涉及5个运动部件——X/Y/Z/A/C轴,共有41项几何误差,其中有30项与位置有关的误差(PDGEs),11项与位置无关的误差(PIGEs),如表1所示。旋转轴误差的定义参照ISO 230-7—2006[20]。表1中,δ为线性误差,ε为角度误差,S为垂直度误差。
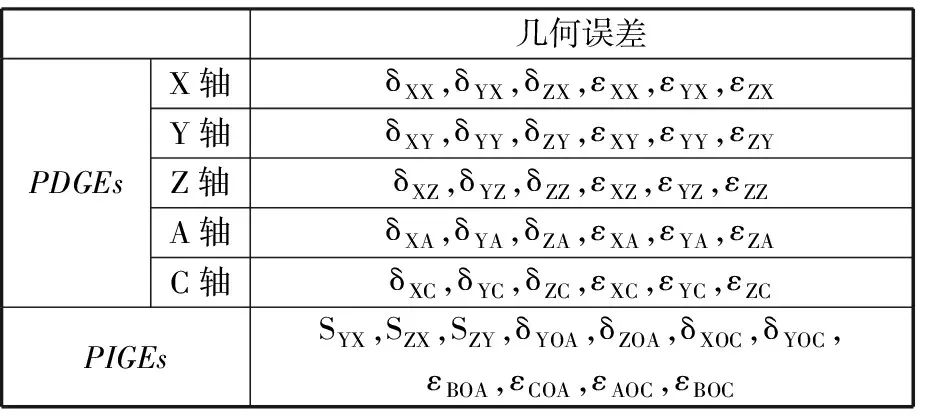
表1 AC双转台五轴数控机床的几何误差列表
在机床实际的运动过程中,由于存在几何误差的影响,刀具的实际切削点相对于工件的空间位置会存在一定的偏差(即机床的体积误差ΔE),可由下式计算得到:
(1)

1.2 机床几何误差建模
本实验中使用激光干涉仪和电子水准仪逐项测量X/Y/Z平动轴的几何误差,利用球杆仪间接测量A/C旋转轴的几何误差,并拟合为位置的三次多项式函数。X轴的6项几何误差模型的表达式如下:
(2)
其中,x为机床X轴的绝对运动量,m;δXX、δYX、δZX为线性误差,m;εXX、εYX、εZX为角度误差,rad。同理,利用其他轴(即Y、Z、A、C轴,其对应的绝对运动量分别为y、z、a、c)的几何误差亦可拟合得到相应的误差模型(各模型的表达式可扫描本文首页OSID二维码获得)。
2 工件分特征下的机床关键几何误差分析
2.1 复杂工件的形状误差建模
图2所示为复杂工件的三维模型,该工件由尺寸分别200 mm×200 mm×10 mm、160 mm×160 mm×10 mm的两个长方体,长宽均为120 mm、坡度为10°的楔体,底面半径为40 mm、圆锥角为30°、倾斜10°的圆锥台以及底面半径为25 mm、高度为10 mm、倾斜10°的圆柱组成。

图2 复杂工件的三维模型
复杂工件的形状误差建模是形状误差分析的前提和基础。如图3所示,首先,基于复杂工件的三维模型进行特征分解,得到平面、斜面、圆柱和圆锥台四个典型特征。然后,基于已规划好的刀具路径,使用UG软件的后处理功能分别获取五轴数控机床加工不同特征时的NC代码。随后,将机床各轴的理想运动量代入式(2)所示的几何误差模型中,即求得刀具路径中每个切削位置上各几何误差的值。最后,将复杂工件的几何误差值代入式(1)所示的体积误差模型中,即可得到其形状误差模型。

图3 复杂工件的特征分解
2.2 工件分特征下的灵敏度分析
本文提出了一种工件分特征下的五轴数控机床关键几何误差分析与补偿方法,用以分析并辨识影响机床加工精度的关键几何误差,并对其进行针对性补偿,进而提高机床的整体加工精度。灵敏度系数的确定是灵敏度分析的前提条件,它对灵敏度分析结果具有决定性的影响。一般来说,一个几何误差的灵敏度系数值越大,说明该几何误差对形状误差的影响就越大。由此可知,进行灵敏度分析之前需定义一个灵敏度系数,各几何误差在不同特征下的灵敏度系数可定义为[21]

(3)
式中,Sn为几何误差n(n=1,2,…,41)在不同特征下的灵敏度系数;[Da,Db]表示加工不同特征时刀具运动的轨迹长度D,其中D=Db-Da;En为仅考虑单一几何误差n得到的形状误差;dL(L=x,y,z,a,c)为对刀具路径上形状误差的微分。
式(3)中,仅考虑单一几何误差n得到的工件形状误差En可由下式表示:
(4)
式中,EnX、EnY、EnZ分别为几何误差n在X、Y、Z方向上的误差分量。
为了便于评估各几何误差对总几何误差的相对影响程度,对每个特征中所有几何误差的灵敏度系数进行归一化处理,定义了归一化灵敏度系数Un,其表达式为
(5)
各特征的41项几何误差的归一化灵敏度系数之和为1。
2.2.1圆锥台特征的灵敏度分析
本文以圆锥台为例,详细阐述了灵敏度分析过程。将工件的三维模型导入到UG中,并设置加工工艺及参数,使用UG的后处理功能获取加工圆锥台时的NC代码,即可得到机床五个轴的理想运动量。圆锥台刀具路径及五个轴的理想运动量如图4所示。

(a)刀具路径 (b)A轴运动量 (c)C轴运动量
将加工圆锥台时机床各轴的理想运动量代入对应的机床几何误差模型中,即可求出圆锥台各位置的几何误差值。最后将圆锥台的几何误差值代入到机床的体积误差模型中,即可得到圆锥台的形状误差。图5a~图5d分别表示由几何误差δYZ、δZZ、δXX、δXA引起的圆锥台形状误差在X/Y/Z方向上的分量。同理,其他几何误差引起的圆锥台形状误差亦可求得。

(a)误差δYZ
由式(3)~式(5)即可求出几何误差δYZ、δZZ、δXX、δXA在圆锥台特征中的归一化灵敏度系数。同理,亦可求出其他几何误差在圆锥台特征中的归一化灵敏度系数。圆锥台特征的灵敏度分析结果如图6所示,可以看出,δYZ、δZZ、δXX、δXA这四项几何误差的归一化灵敏度系数之和为0.6。其中,几何误差δYZ的归一化灵敏度系数为0.262,远大于其他几何误差对圆锥台形状误差的影响,因此在后续的补偿过程中,对几何误差δYZ的补偿是需要重点考虑的。

图6 圆锥台特征的灵敏度分析结果
2.2.2圆柱特征的灵敏度分析
同理,按照上述灵敏度分析方法,可得到各几何误差在圆柱特征中的归一化灵敏度系数,分析结果如图7所示,可以看出,δYZ、δZZ、δXX这三项几何误差的归一化灵敏度系数之和为0.54。其中几何误差δYZ的归一化灵敏度系数为0.295,远大于其他几何误差对圆柱形状误差的影响,因此在后续的补偿过程中,对几何误差δYZ的补偿是需要重点考虑的。

图7 圆柱特征的灵敏度分析结果
对比图6和图7可得,圆柱和圆锥台特征中,归一化灵敏度系数大小排在前三的几何误差均相同,依次为δYZ、δZZ、δXX,但其他几何误差的影响却是不同的,并且圆柱和圆锥台特征中相同几何误差的归一化灵敏度系数值亦不相同。由此可知,对于有典型特征的工件,分特征地进行灵敏度分析可有效地辨识几何误差之间的差异,为后续补偿提供更加准确的数据支撑。
本文定义归一化灵敏度系数大于0.03的几何误差为关键几何误差,从图6和图7中可得到影响圆柱和圆锥台的关键几何误差,结果如表2所示。从表2中可知,对于圆柱特征,共有12项关键几何误差,其中线性误差有11项;对于圆锥台特征,共有11项关键几何误差,其中线性误差有9项。由此可认为线性误差是影响圆柱和圆锥台形状误差的重要因素。

表2 影响圆柱和圆锥台关键几何误差
2.2.3平面与斜面特征的灵敏度分析
由于机床的PIGEs为与位置无关的几何误差,PDGEs为与位置有关的几何误差,则在本实验中,平面和斜面的加工只需平动轴X/Y/Z运动,而旋转轴A/C不动,因此旋转轴的PIGEs对平面和斜面的几何误差有影响,而PDGEs对其无影响。
根据2.2.1节中求取圆锥台的几何误差灵敏度系数的方法,同理亦可求出各几何误差在平面和斜面特征中的归一化灵敏度系数,结果分别如图8a和图8b所示。对比图8a和图8b可得,平面和斜面特征中,两者的关键几何误差较为相似,其中δZZ、δYX、δXY、δXX这四个几何误差的归一化灵敏度系数之和约占总和的50%。平面和斜面特征中相同几何误差的归一化灵敏度系数大小是不同的,其中关键几何误差SZY、δYY、SYX、δZX、SZX的灵敏度系数的数值大小有所差异。

(a)平面特征
在上述分析的基础上,可得到影响平面和斜面特征的关键几何误差,如表3所示。从表3中可得,对于平面特征,共有10项关键几何误差,其中线性误差有6项;对于斜面特征,共有11项关键几何误差,其中线性误差有6项。由此可认为线性误差是影响平面形状误差和斜面形状误差的重要因素。

表3 影响平面和斜面特征的关键几何误差
3 工件分特征下的机床关键几何误差补偿实验
由上述分析可得,平面、斜面、圆柱和圆锥台四个特征的关键几何误差归一化灵敏度系数之和占比均大于90%,分别为91.9%、92.1%、90.4%和90.8%。将上述辨识得到的四个特征的关键几何误差分别代入到机床的体积误差模型中,计算其在总误差中的占比,结果如表4所示。
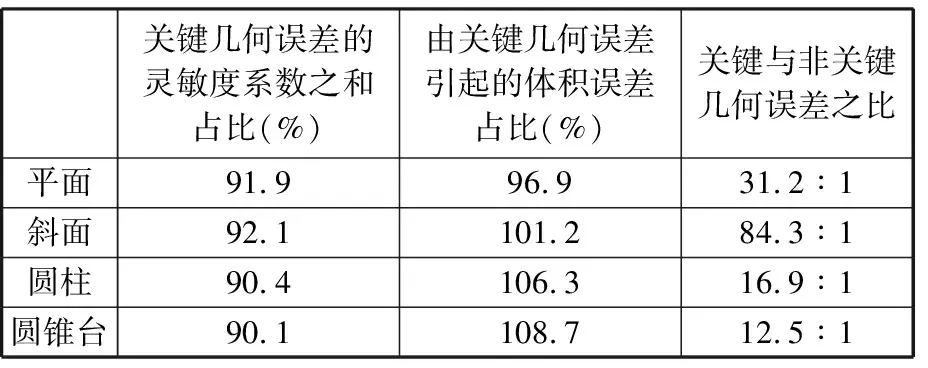
表4 关键几何误差占比分析
表4中,由关键几何误差引起的体积误差占比在斜面、圆柱和圆锥台特征中均大于1,表明由非关键几何误差引起的体积误差占比分别为-1.2%、-6.3%、-8.7%,即说明关键几何误差与非关键几何误差对体积误差中的作用效果相反。对比表4中结果可得,关键几何误差占比远大于非关键几何误差占比,因此关键几何误差对体积误差的影响起决定性作用,从而验证了本方法的正确性。
本文在一台型号为JDGR400 AC双转台五轴数控机床上开展切削与补偿实验。将平面、斜面、圆柱和圆锥台四个特征的关键几何误差分别代入式(1)所示的机床体积误差模型中,参考文献[22]中的方法,基于逆运动学计算补偿后各轴的运动值,从而得到补偿后的NC代码。图9所示为使用补偿后的NC代码进行切削加工的复杂工件。

图9 补偿后的复杂工件
按照图10a所示的测点分布,在ZEISS三坐标测量机上对图9所示的复杂工件补偿前后的四个典型特征分别进行标定,如图10b所示。补偿前后的四个典型特征误差平均值及补偿率如表5所示。补偿后四个特征的误差平均值分别为8.8 μm、26.8 μm、4.9 μm和14.8 μm,其加工精度提高20%~30%,从而验证了该方法的可行性与有效性。

(a)测点分布 (b)三坐标标定

表5 补偿前后的四个典型特征误差平均值及补偿率
4 结论
(1)对于复杂工件的不同特征而言,影响工件形状误差的关键几何误差虽有相似之处,但同一几何误差的归一化灵敏度系数在不同特征中的大小并不相同,因此在误差补偿中,对不同特征的工件应区别考虑。
(2)在分析得到的关键几何误差中,大多数几何误差为线性误差,因此可认为线性误差是影响平面、斜面、圆柱和圆锥台这四个特征形状误差的重要因素。
(3)对于平面和斜面特征,其关键几何误差的归一化灵敏度系数分布较均匀;对于圆柱和圆锥台特征,影响较大的前三项关键几何误差δYZ、δZZ、δXX的归一化灵敏度系数在总误差中的占比较大,可达到50%以上。
(4)基于JDGR400 AC双转台五轴数控机床的误差补偿实验结果表明,补偿后工件四个典型特征的加工精度提高了20%~30%。由此可知,本文提出的工件分特征下的灵敏度分析与补偿方法能有效地提高机床的加工精度。

