基于分布活化能模型法的农林生物质热解动力学对比研究

乔 沛 ，郭子千 ，张玉明,* ，李家州 ，张 炜 ，刘明华

（1. 中国石油大学(北京) 重质油国家重点实验室, 北京 102249；2. 福州大学 环境与资源学院, 福建 福州 350108）

近年来，由于化石资源消耗和化石燃料导致地球气候破坏的趋势，对可持续能源的行动达到了新的高度[1]，其中，生物质成为了仅次于煤炭、石油、天然气的世界第四大能源，过去十年内生物质能源消费量在亚太及非洲地区分别实现了14.0%和8.9%的年均增长率[2]，为了应对这一能源形势，中国在2020 年正式提出“2030 年前碳达峰、2060年前碳中和”的战略目标[3]。生物质作为唯一的可再生含碳资源在推广利用的同时，可以在一定程度上保障中国“双碳战略目标”的顺利执行。

木质纤维素类生物质具有高热量、高固定碳含量、易于处理等优点，其中，农林生物质与大家的生活息息相关，目前，得到越来越多的关注[4]。热解反应作为生物质热转化方法的先导步骤，通常在低于气化和燃烧的温度范围（673−973 K）和较低的压力（0.1−0.2 MPa）下进行[5,6]，可以将生物质转化为生物质炭、不可凝气体和生物油等高价值的能源产品[7,8]。热重质谱联用技术（TG-MS）可用于获得惰性气体下生物质分解的失重特性曲线以及热力学参数[9]，在线检测特定温度下热解的气体产物，对热解过程中的逸出气体进行定性与定量分析[10,11]。通过失重数据确定生物质热解过程的全局及局部动力学参数，可用于明确热分解过程并了解热解反应中的产物形成，还可用于热解反应器的设计和优化[12]。

许多研究对生物质热解机理、行为及动力学进行了探讨。生物质的主要成分是纤维素、半纤维素、木质素、无机物和一些提取物，它们在热解过程中具有反应行为不同，发生分解的温度差别较大[13]。木质纤维素生物质的热解过程可分为三个主要区域：水分和极轻挥发物去除阶段（25−175 ℃）、主动热解阶段（175−400 ℃）及被动热解阶段（＞ 400 ℃），在主动热解阶段内主要为半纤维素及纤维素的分解，温度分别为175−380 ℃和250−400 ℃，而木质素的分解通常发生在180−900 ℃的广泛温度，以较慢的速率发生，在被动热解阶段主要为木质素的分解[14,15]。热解过程中主要的失重发生在第二阶段，是由于生物质组成的聚合物结构中弱键发生热断裂反应，形成更强、更稳定的化学键，在木质纤维素生物质中主要对应半纤维素与纤维素的分解反应[16,17]。Mészáros等[18]对木材样品中获得的抽提物进行热解反应特性研究，发现抽提物的热解发生在较宽的温度范围（150−550 ℃）内，其热解产生的产物包括CO2、CO、CH4、CH3O+、CH3CO+、脂肪碎片等，影响了最终产物分布。

生物质热解动力学分析方法主要分为无模型法和模型拟合法[19,20]，两种方法能够在很大程度上互相补充[21]。Vyazovkin 等[19]指出模型配合法可以与实验数据充分拟合，但有时存在动力学参数的不确定性。这种不确定性可以通过等转化率方法进行避免，因此，等转化率法成为当前生物质热解动力学中，分析单一反应的最常用方法[22]。等转化率法还可以分为微分法和积分法两类，其中，Friedman 微分法由于简单、精度高等优点，成为应用最广泛的等转化率方法[23]。Flynn-Ozawa-Wall（FWO）积分法因为计算简便同样得到了大量使用，但在推导时采用了过于简单的温度积分近似，导致活化能存在明显误差[24]。等转化率法计算数据量较多，通常需要在至少四种不同加热速率下进行多次实验来保证结果精度，其结果也不能很好地识别生物质热解过程的复杂多步反应[25,26]。

分布活化能模型（DAEM）法作为一种精度较高的动力学分析方法，被用于描述复杂的、多步骤的热解反应。DAEM 法假设热解过程中存在一系列不可逆平行反应，用于解释热解反应的复杂性和多样性[27,28]，通过对其若干组分动力学参数（指前因子、活化能）计算复杂反应的动力学分析[29]。DAEM 法弥补了等转化率法在多步反应中的计算局限性。等转化率法与DAEM 法进行动力学对比计算可以对农林类生物质热解反应形成更加全面的认识。

Singh 等[30]利用四种等转化率法计算出油桐的平均活化能为211−221 kJ/mol。Mishra 等[31]采用四种动力学模型对大丽花热解参数进行求解，KAS 法、FWO 法、Friedman 法和DAEM 法求得指前因子分别为1.69×1016、5.94×1020、6.30×1018和7.72×1016，活化能分别为220.12、229.81、222.57 和232.78 kJ/mol。Xavier 等[32]按照生物质原料中的四种组分半纤维素、纤维素、木质素和提取物，采用独立平行反应模型（IPRM）研究了澳洲坚果的热解反应特性，结果表明，在10 K/min 的升温速率下，四种组分的指前因子分别为2.9×109、1.1×1019、8.9×102、2.8×1016，活化能分别为132.2、258.3、65.8 和199.5 kJ/mol。当前大多数研究缺乏对各类动力学计算方法的对比，同时计算结果与生物质组分缺乏有效的关联，难以形成各类农林生物质热解过程及其动力学的系统性认识。

本研究选用三种典型的农林类生物质，采用TG-MS 分析仪对热解特性及气体释放行为进行对比，在此基础上选取典型等转化率法（Friedman 法及FWO 法）和DAEM 法对热解动力学进行全面分析。通过三种农林生物质及其各类动力学计算方法的对比，深化了典型农林类生物质热解反应及动力学特性的总体认识。

1 实验部分

1.1 实验样品

选取杏壳（AS）、小麦秸秆（WS）以及杨树木屑（PS）三种农林类生物质作为实验原料。将实验原料破碎后筛选出粒径小于80 目的颗粒，在105 ℃下干燥12 h 后放入干燥器中备用。三种生物质的工业分析、元素分析如表1 所示，采用文献中对生物质组分定量测定的方法进行组分分析[33]，结果如表2 所示，从中可知半纤维素、纤维素以及木质素在杨树木屑中的分布更为均衡，杏壳和小麦秸秆则分别以木质素（43.86%）和纤维素（53.84%）为主。小麦秸秆中所含的灰分（5.76%）高于杏壳（3.83%）和杨树木屑（1.50%），杨树木屑中的提取物含量（6.51%）明显低于其他两种原料。

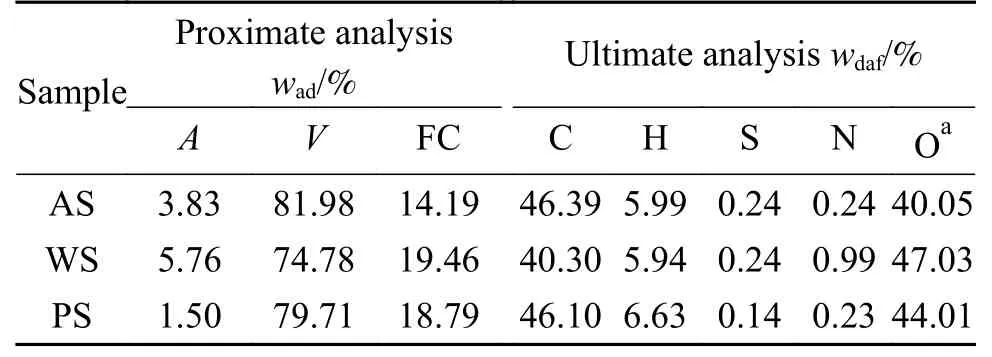
表1 生物质的工业分析和元素分析Table 1 Proximate and ultimate analyses of biomass

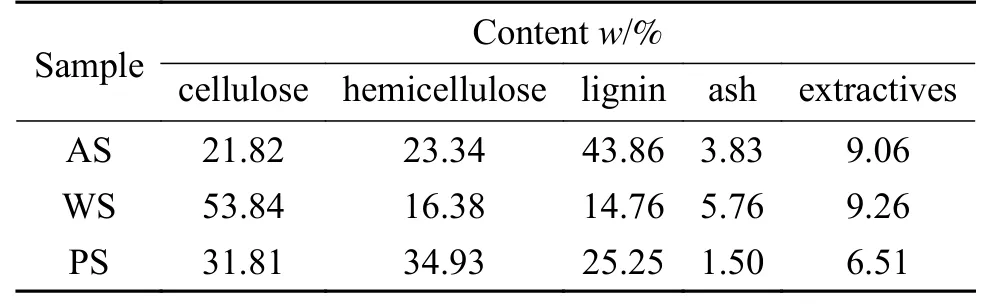
表2 生物质的组分分析Table 2 Component analysis of biomass

1.2 热解实验

采用法国SETARAM 公司的LABSYS EVO 型热重分析仪与美国TILON 公司的SRD 质谱仪组成TG-MS 联用仪，在100 mL/min 的氮气均匀气流中进行热重分析实验，采用较低的样品质量（4−6 mg）及较小的原料粒径（80 目）最大化降低热解过程中的热滞后问题。待热重系统稳定后，将样品放置在Al2O3坩埚中，通氮气吹扫15 min 后以不同升温速率（10、20、30、40 ℃/min）从室温升高至900 ℃，选取20 ℃/min 下的气体释放参数进行分析，每组实验重复三次以保证各组之间误差不大于5%。由于在120 ℃之前三种生物质的失重主要来自于水的脱除，对于热解动力学计算的贡献很小，而热解失重起始温度为150−200 ℃，因此，选取脱水过程结束后的原料质量作为初始值进行归一化处理，并在后续的动力学计算过程中选取120 ℃之后作为研究的温度区间，归一化后的热解失重速率曲线如图1 所示。

1.3 等转化率法

动力学参数活化能与指前因子可以通过基本速率方程和阿伦尼乌斯方程联立得到的动力学分析方程确定，速率方程可以表示为[34]：

式中，k为速率常数，α为在t时刻的原料转化率，f(α)代表反应机理模型函数。而速率常数k与温度的变化关系可以表示为：

式中，A为指前因子，Ea为该反应的活化能，R为气体常数，T为t时刻的绝对温度。因此，方程(2) 可以与方程(1)联立：

根据动力学分析中使用数据的不同，可以将动力学分析分为微分法和积分法，方程(3)使用微分法，表示原料的质量损失率取决于温度，而使用积分法可以表示为如下所示：

式中，β是热重实验时的恒定升温速率。研究表明，生物质热解反应可以使用一阶反应模型来实现较好的匹配效果，本文假设三种生物质的热解反应均遵循一阶反应模型[35,36]。

选用Friedman 法和FWO 法进行分析。Friedman法的方程可以通过对数的形式表示[37]：

等式左边的ln(β·dα/dt)对1/T作图可以获得相同转化率时点的线性拟合，通过相应直线的斜率可以确定给定转化率下的活化能。

FWO 法[38,39]是一种等转化率积分法，可以采用如下积分方程：

将方程(9)用对数的形式进行表示如下：

lg[p(Ea/RT)]可以用方程(11)来近似：

因此，FWO 法可以简化为：

可以对上式中的lgβ与1/T作图，每个转化率下的活化能可以通过所作直线的斜率来求解。

1.4 分布活化能模型法[37]

生物质热解由反应速率不同的平行顺序反应组成，因此，简单动力学模型不能准确描述热解过程，故采用DAEM 法对生物质原料的热解动力学进行更准确的分析。生物质热解各组分的独立反应均符合一阶反应模型，因此，采用一阶DAEM 模型来进行求解，方程如下：

采用常用的高斯分布函数来表示活化能分布，采用平均活化能E0和标准差σ来表示活化能分布函数f(Ea)，同时分布函数需满足条件如下：

将指前因子确定为固定值，因此，方程(13)可以表示为：

由于生物质热解过程组分较多，反应复杂，本文采用四组分高斯型DAEM 方法进行研究，其活化能模型可以表示为：

传统DAEM 方法（Miura 微分法）在计算时需要不同加热速率下的瞬时dα/dT值，对于实验噪声较为敏感[24]。本文对传统DAEM 方法进行改进，仅需要单一升温速率下的实验数据，并采用模式搜索法对f(Ea)进行自动寻找，避免了人为指定活化能数值范围带来的误差，实现了动力学参数的优化[40]。

定义S值如式(17)所示，当S值随着迭代次数增加没有明显变化时判定达到最优拟合值，设置拟合度偏差值Fit作为评价模型拟合程度的标准，该值越低说明求取动力学参数的准确度越高。式中i为研究的数据点，n为数据点的个数，(dα/dT)max表示实验求出的转化率导数的最大值。

公式(18)是根据S值定义了动力学参数拟合度偏差Fit值，能够更清晰对比拟合结果的精度，Fit值越小，拟合精度越高。

2 结果与讨论

2.1 热解特性及气体释放行为

图2为三种生物质在不同升温速率（10、20、30、40 ℃/min）下的TG-DTG 曲线。三种生物质的热解行为与文献中基本一致，并在反应第二阶段表现出明显的失重现象以及较高的失重速率[14,15]。由于多种反应在不同程度上重叠在一起，图2 (a)右图中杏壳的DTG 曲线呈现出明显双峰结构，图2 (b)和(c)中的DTG 曲线则表现为较矮肩峰和单一峰的结构，其中，较矮的肩峰可以对应半纤维素的分解，较高的峰则归因于纤维素的分解。DTG 曲线外观不仅取决于热解过程的传热传质，还与生物质中多种组分的分子结构和化学性质有关，木质素作为纤维素与半纤维素的结合剂，木质素含量的增加可以使得DTG 曲线中双峰的分离性更明显[15]，杏壳DTG 曲线呈现出明显的双峰分布。

对三种生物质20 ℃/min 升温速率下热解小分子气体产物（CO2、H2O、CH4、C2H6、H2、CO）进行检测，气体产物释放曲线如图3 所示，可以发现，三种生物质热解反应的气体释放规律基本一致。在120 和350 ℃附近均出现了水蒸气逸出峰，前者来自于生物质中结合水的释放，而后者主要来自于纤维素内部的氢键断裂与羟基脱水反应，同时发生脱羰基反应。半纤维素和纤维素中羰基和羧基的分解，使得CO 及CO2气体逸出峰出现在350 ℃附近，在700 ℃之后CO2仍在进行释放，这主要来自于芳烃取代基、醚结构和含氧杂环的破坏。在500 ℃之后主要发生木质素的分解，木质素中苯丙烷侧链上醚键和苯环间醚键断裂，使得CO 在较宽的温度范围内均有释放。

三种生物质的tmax均在360 ℃左右，该温度下有大量的有机物质分解为大分子有机物，并释放出大量的H2O、CO 和CO2。在420 ℃时纤维素与半纤维素基本分解完全，产生的大分子有机物裂解反应和二次缩聚反应加剧，甲基侧链断裂，长链脂肪烃断链、环烃芳构化等反应大量进行，表现为CH4、C2H6、H2的释放。其中，CH4在高温区较宽范围内存在释放信号，一部分来自木质素中甲氧基的裂解；另一部分则归因于脂肪族和芳香族结构的缩合反应。由于木质素中甲氧基−O−CH3含量比半纤维素及纤维素更多，CH4的释放主要来自木质素的热解[15]，因此，杏壳中较高的木质素含量表现为更高的CH4释放峰。

三种生物质的热解特征参数如表3 所示，表中β–升温速率，ts–主反应开始温度，tmax–最大失重速率对应温度，tf–主反应结束温度，(dα/dt)max–最大失重速率，Δαmax–总失重率，Δα–主反应区间挥发分转化率变化量。随着升温速率的提高，同种生物质热分解主反应的起始温度和结束温度均向着高温区进行了移动，以杨树木屑为例起始温度从186 ℃提高到了202 ℃，结束温度则从399 ℃提高到了429 ℃，tmax呈现出相同的变化趋势。尽管对原料粒径及用量做出限制，但不同升温速率导致的热滞后现象仍无法彻底消除，生物质热解在颗粒表面到内部存在一个温度梯度，随着升温速率的提高，相对传热时间变少，外层的热量不能及时传递到颗粒内部，扩大了内外表面之间的温度梯度和温差，产生了明显的热滞后现象。升温速率的提高也促进了挥发分的释放，三种生物质热解最大失重速率分别从对应的0.13%、0.18%和0.16% s–1提高到40 ℃/min 下0.49%、0.54%和0.56% s–1。

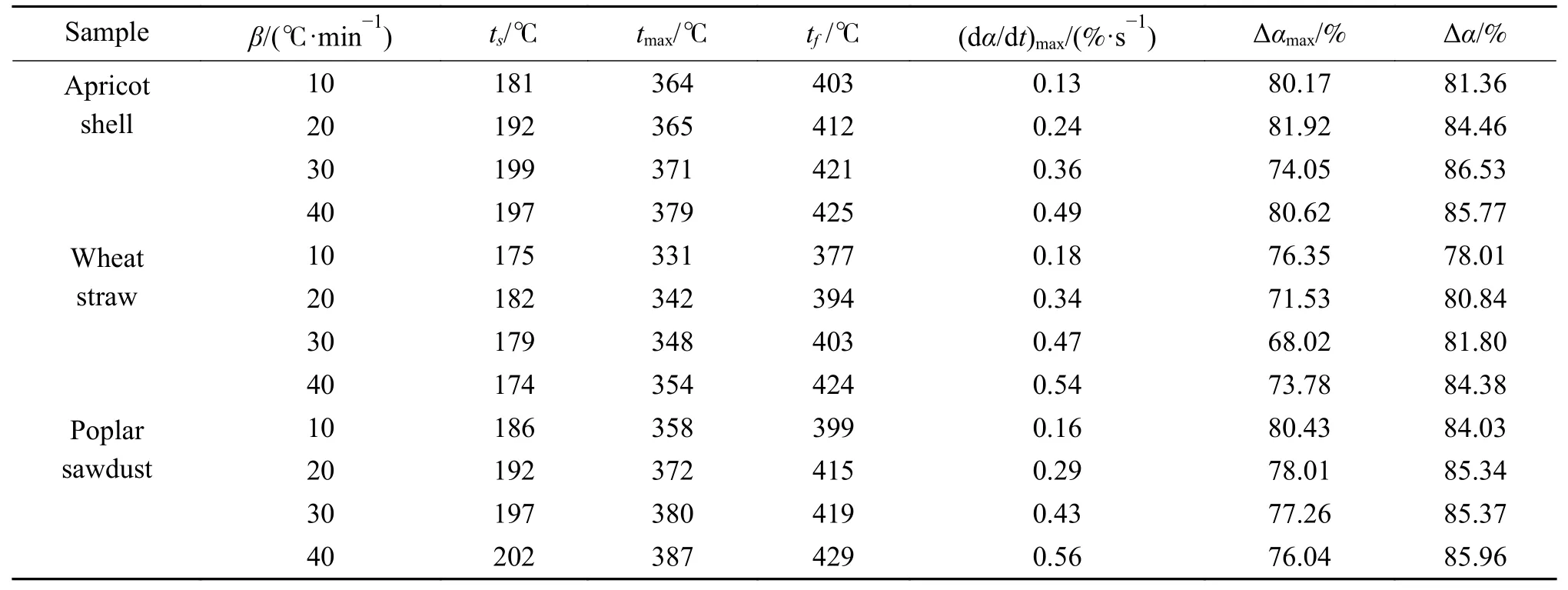
表3 不同升温速率下的热解特征参数Table 3 Pyrolysis characteristic parameters at different heating rates

生物质灰分中部分金属组分的催化作用能够降低热解温度[41]，小麦秸秆中灰分含量（5.76%）高于其他两种生物质（3.83%、1.50%），因此，其主反应区间（175–377、182–394、179–403、174–424 ℃）明显小于杏壳（181–403、192–412、199–421、197–425 ℃）与杨树木屑（186–399、192–415、197–419、202–429 ℃），tmax也呈现出同样的规律。杏壳（81.98%）与杨树木屑（79.71%）中的挥发分含量相近，均高于小麦秸秆（74.78%）中的挥发分含量，以20 ℃/min 的升温速率为例，前两者在主反应区间内的挥发分转化率变化量（84.46%、85.34%）也高于小麦秸秆（80.84%）。

三种生物质的热解过程中转化率随着温度变化的曲线如图4 所示，不同升温速率下各曲线均表现为S 型分布，与图2 中各生物质的DTG 曲线进行对比可以发现，在200–400 ℃转化率迅速增加，这一阶段的整体挥发物转化率分别从81.36%、78.01%、84.03%增加到了85.77%、84.38%、85.96%。可以证明随着升温速率的提高，在主反应区间内，挥发分的停留时间越长越有利于二次反应的进行从而生成炭。但随着温度的升高，在缓慢炭化阶段较慢的升温速率能够保证木质素等主要反应物有着充分的时间进行分解反应，将更有利于挥发分的释放，因此，从表3 中可以看到，随着升温速率的提高，生物质颗粒之间传热滞后使得总失重率从80.17%、76.35%、80.43%分别减少到了74.05%、73.78%、76.04%。

2.2 等转化率法计算动力学参数

采用Friedman 法和FWO 法在转化率为0.1−0.8 的条件下，以0.05 为间隔进行农林生物质动力学参数的分析计算。图5、图6 分别为两种等转化率法的拟合曲线，表4 为计算得到的动力学参数。转化率接近0.8 时，此时热解反应即将结束，仅剩部分残留的半纤维素和纤维素，主要失重来自与少部分有机物和其他残留物的分解以及大部分不能反应的无机物。因此，动力学分析时不考虑转化率α＞0.8 时的实验数据。

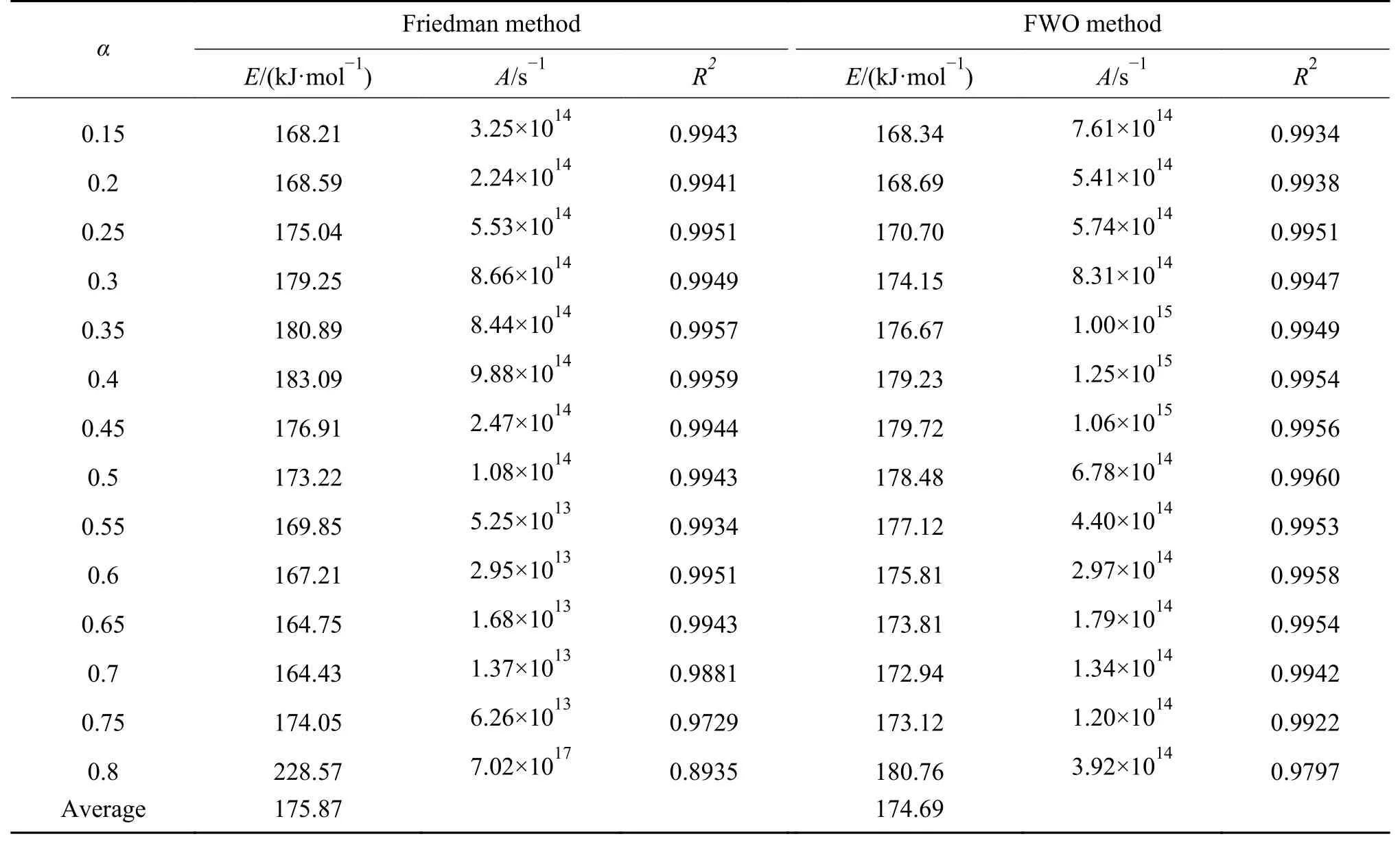
表4 Friedman 法和FWO 法求得的动力学参数 （续表4）

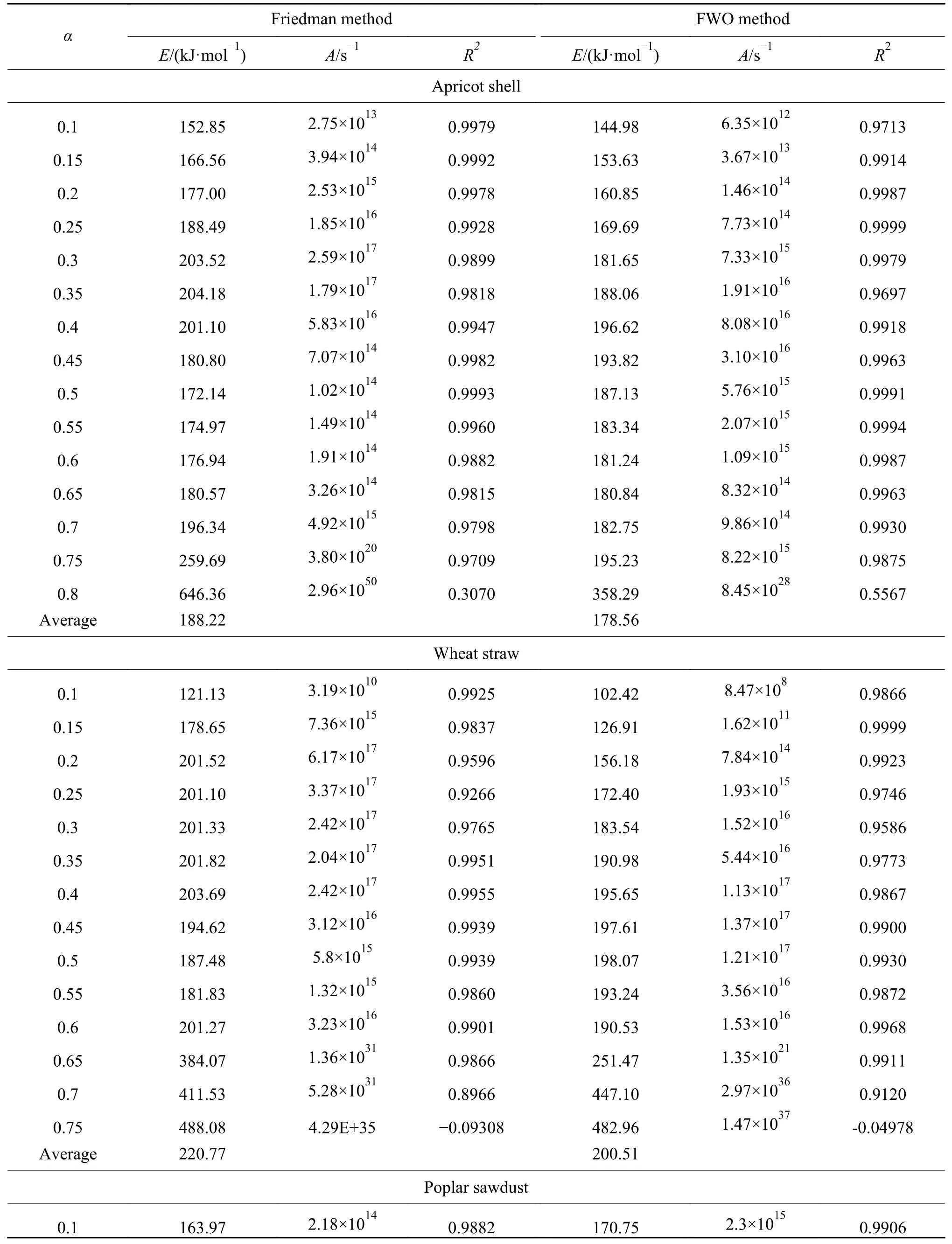
表4 Friedman 法和FWO 法求得的动力学参数Table 4 The kinetic parameters obtained by Friedman method and FWO method

从图5 和图6 可以看出，由两种等转化率法计算所得不同转化率下的多条线性拟合直线并不完全平行，说明三种木质素纤维素生物质的各个组分之间相互作用，总体失重特性是包含多个反应的综合过程。尤其当转化率很高（大于0.6）时，拟合直线的平行度越来越低，说明随着生物质转化率升高，其多组分反应的特性越来越明显[42]。

Friedman 法求得三种生物质的平均反应活化能分别为188.22、220.77 和175.87 kJ/mol，FWO 法求得的平均反应活化能分别为178.56、200.51 和174.69 kJ/mol，可以发现，FWO 法求活化能低于Friedman 法。主要是由于积分法与微分法的近似和假设方法的区别所导致的，通常情况下认为Friedman 法中不存在引入温度积分导致的系统误差，其对于热解动力学的分析更准确[9]。

图7为两种等转化率方法求得活化能随着转化率变化的曲线，整体在150–200 kJ/mol。三种生物质的活化能变化拐点均在转化率0.4 处出现，这是因为在热解初期主要为半纤维素和纤维素的热解，反应活性较强。随着反应程度的加深，活性降低，同时热解气体产物受到固体焦炭孔隙的影响而产生一定的阻力，也会使得所需活化能升高[43]。由于在转化率为0.1–0.2 的条件下生物质热解活化能主要体现为半纤维素的热分解反应，降解首先从化学链较弱的部分开始，随着弱链的减少活化能逐渐升高，木质素与半纤维素之间的相互作用使该区间内活化能升高[44]。由于小麦秸秆中半纤维素含量较少，活化能从121.13 升高到201.52 kJ/mol，变化幅度较明显，同时杏壳中木质素含量明显高于其他两种生物质，因此，其活化能涨幅（152.85–177.00 kJ/mol）也明显高于木屑（163.97−168.59 kJ/mol）。转化率为0.2–0.6 时的平均活化能分别为杏壳186.57与182.49 kJ/mol，小麦秸秆197.19 与186.46 kJ/mol、杨树木屑174.89 与175.62 kJ/mol，呈现出“秸秆＞杏壳＞木屑”的规律，由于木质素会使不同组分之间结合更加紧密，而生物质中不同含量的灰分同样会影响分解的过程，因此，造成活化能的不同。

在高转化率条件下少量残留物热反应的活化能数值较大，推测在生物质中存在某些难以热解的特征组分。根据表1 中三种生物质组分的分析，杏壳与小麦秸秆中提取物的含量明显高于杨树木屑，杨树木屑在转化率0.8 时相关系数的偏差程度较小，活化能没有出现较大幅度的增加。Xavier等[32]认为，提取物在热解反应过程中对于失重的贡献作用不亚于木质素的分解，杨树木屑原料中提取物的低含量使其在较高转化率时能够保持动力学参数的偏差较小。采用等转化率法可以获得生物质热解反应的整体表观活化能及其随转化率的变化关系，但在计算时将反应视作单一反应的假设与生物质多组分特性相违背，将导致计算得到的动力学参数与实际数据之间存在一定的误差，并不能获得各组分在热解反应中的动力学参数。

2.3 分布活化能模型法计算动力学参数

在转化率较高时生物质中部分特征组分导致了计算过程中较大偏差的存在，等转化率法无法从生物质组分的角度对这一偏差进行解释。本研究选取10 ℃/min 升温速率时的数据进行DAEM计算，根据表1 和表2 中原料组成特性，假定杏壳、小麦秸秆和杨树木屑均包含四种虚拟组分，使用高斯型DAEM 进行四组分拟合，拟合结果如图8 所示。

图8给出了分布明显的四组分拟合峰，三种物质DTG 曲线中半纤维素及纤维素的峰位置处均存在对应的虚拟组分拟合峰2 和3（CNT2、CNT3），在较宽的温度范围内均存在一个较扁的组分拟合峰1（CNT1），并在400 ℃之后的缓慢炭化阶段成为失重的主要虚拟组分，在转化率较高的温度范围内出现峰面积较小的虚拟组分峰4（CNT4）。四种虚拟组分拟合峰叠加得到的拟合曲线CAL 与实验曲线EXP 基本重合。

区别于传统DAEM 方法指定活化能或指前因子进行计算的方式，本研究采用模式搜索法在指定数量级范围内对动力学参数进行计算，如表5所示。结果表明，本研究除虚拟组分CNT4 之外，CNT1、CNT2、CNT3 的相关系数R2均大于0.99，动力学参数拟合度偏差Fit值（公式(18)）均在5 以下，虚拟组分CNT4 由于其峰面积c4较小（0.0524、0.0998 和0.0977），Fit值较不稳定，但R2值仍在0.9 以上。该方法对虚拟组分的计算可以更好的与实验数据对应。

由表5 可知，三种生物质中各虚拟组分的平均活化能均呈现出E1＜E2＜E3＜E4的规律，根据Vamvuka 等[45]的研究，半纤维素和纤维素热解的平均活化能为90–125 kJ/mol 和145–285 kJ/mol，木质素在温度较低时便开始分解，反应活化能低于半纤维素。CNT4 的平均活化能E4较高（297.44、284.35 和309.96 kJ/mol），并不在纤维素的平均活化能分布范围内。生物质中的提取物成分复杂，且在250–550 ℃进行热分解反应，与半纤维素、纤维素以及木质素有一定的重合，并在320–400 ℃存在明显的CH4和C2H3+占主导地位的失重峰[18]。结合图8 中各拟合峰位置，可以将各虚拟组分可以与生物质原料中的实际组分进行对应，平均活化能规律表现为：木质素（CNT1）＜ 半纤维素（CNT2）＜纤维素（CNT3）＜ 提取物（CNT4）。

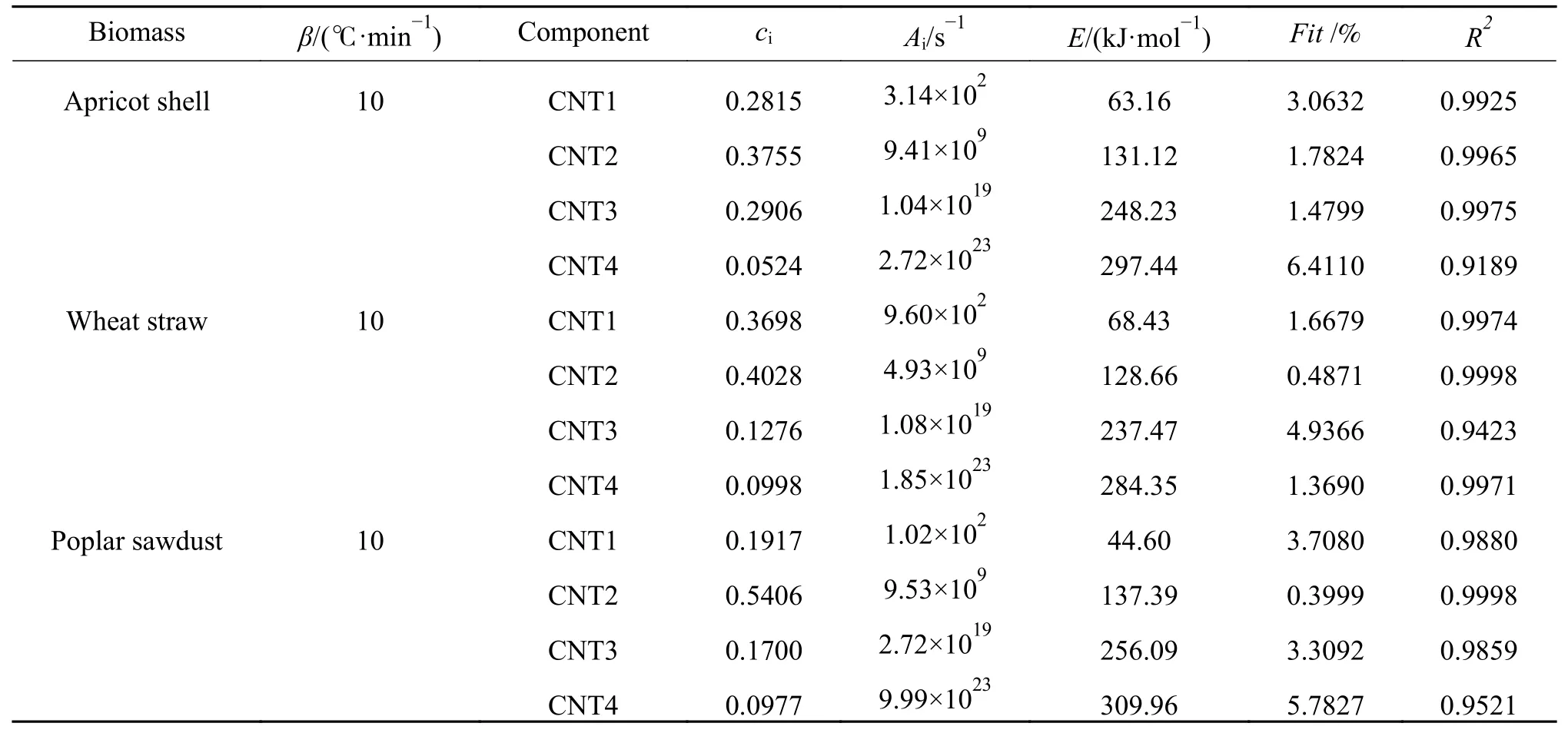
表5 四组分DAEM 动力学参数及评价指标Table 5 Kinetic parameters and evaluation indexes from four-component DAEM method

三种生物质中各虚拟组分的热解特征参数如表6 所示。杏壳、秸秆与木屑的半纤维素ts分别为198、183 及195 ℃，tmax分别为299、402 及431 ℃，纤维素的ts分别为276、273 及286 ℃，tmax分别为344、321 及360 ℃。秸秆中半纤维素与纤维素ts低于杏壳与木屑，纤维素tmax存在秸秆＜杏壳＜木屑的关系。由于生物质灰分中的无机矿物组分对于热解反应具有催化作用，三种生物质中灰分含量存在秸秆（5.76%）＞杏壳（3.83%）＞木屑（1.50%）的关系。以上结果表明，生物质中灰分的催化作用主要体现在降低初始热分解的反应温度，同时催化降低了半纤维素与纤维素的平均活化能，总体上呈现出小麦秸秆＜杏壳＜杨树木屑的变化规律。

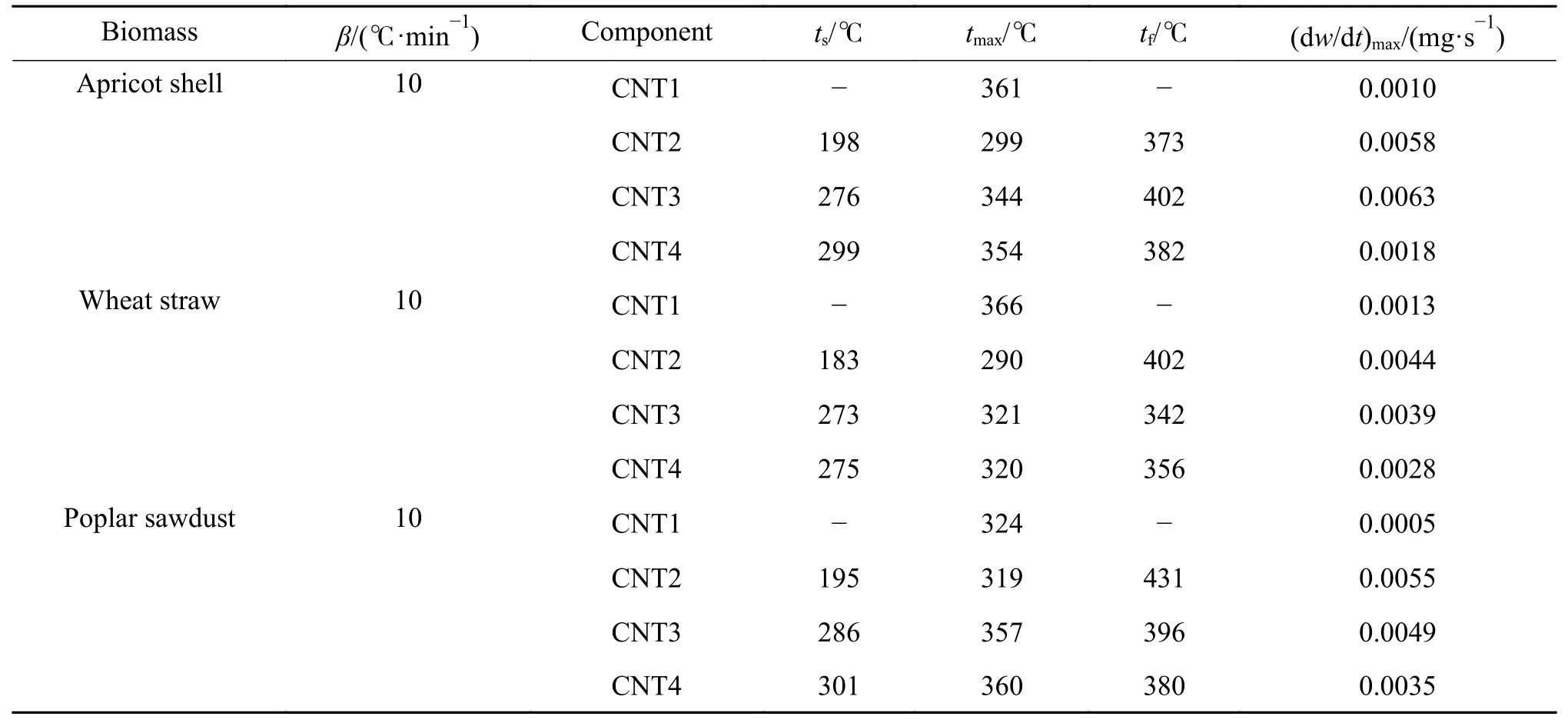
表6 虚拟组分热解特征参数Table 6 Pyrolysis characteristic parameters of pseudo-components

2.4 热解动力学对比

本研究活化能计算结果与相关文献对比如表7所示。其中，典型的热解动力学计算模型包括以等转化率法（Friedman 和FWO 等）[31,45]和简化分布活化能模型（sDAEM）法[31,45]为代表的单反应动力学模型，活化能数值用ES表示（Activation energy for single reaction）；以多组分分布活化能（DAEM）法和平行反应模型（IPRM）法为代表的多反应动力学模型，活化能数值用EM表示（Activation energy for multiple reaction）。

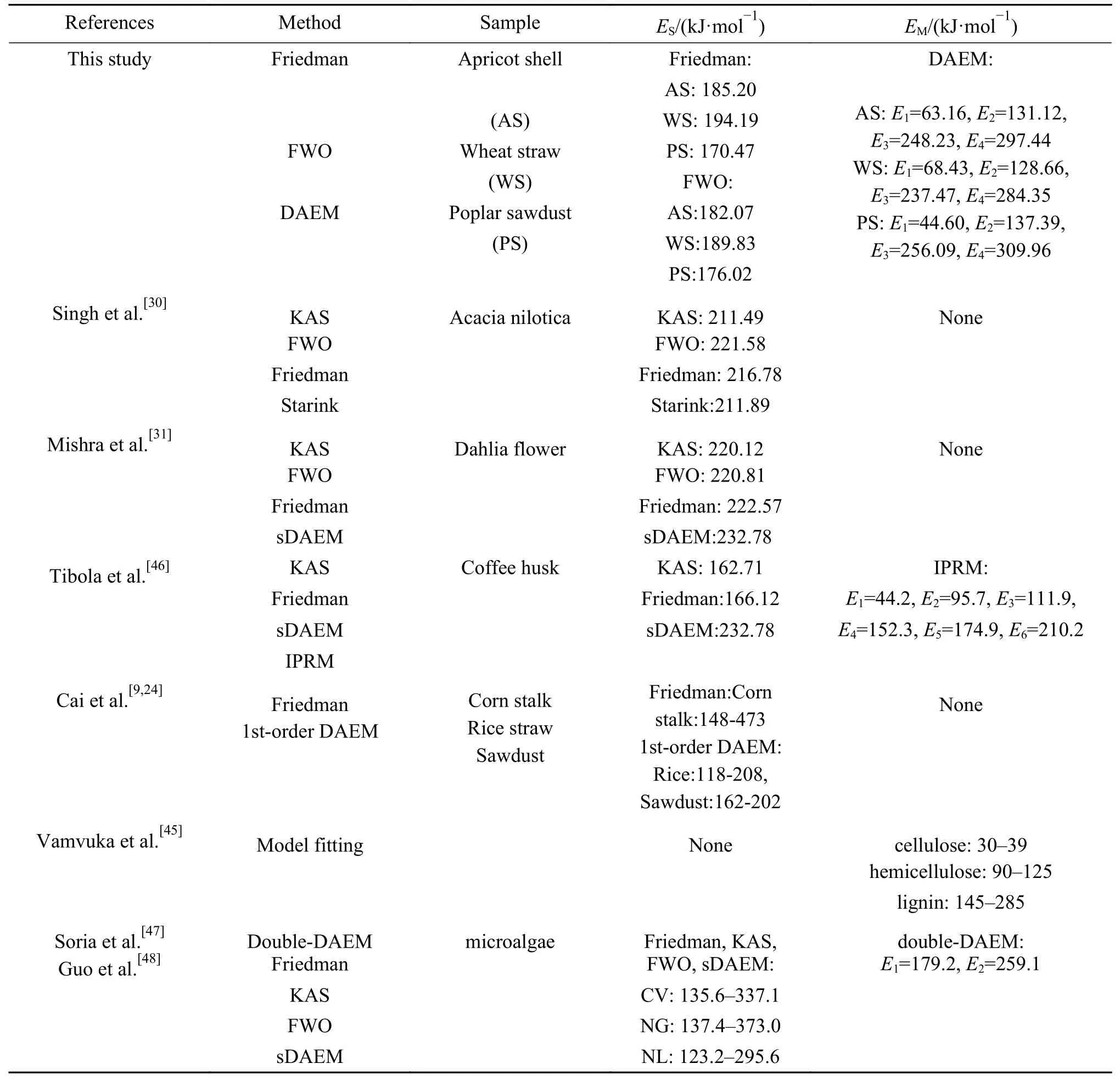
表7 本研究中的活化能与文献中结果的对比Table 7 Activation energy comparison between this study and the results in literature

本研究采用Friedman 法及FWO 法求得生物质的活化能与相关研究结果基本相同[9,30,31]，Mishra等[31]和Tibola 等[46]使用sDAEM 法，Cai 等[9,24]使用1st–DAEM 法将生物质热解反应当作单组分反应进行计算，得到的活化能分布范围与等转化率法得到的分布范围基本相同。采用1st-DAEM 法求得稻壳与木屑总体活化能为118–208 kJ/mol、162–202 kJ/mol，与本文等转化率法所得平均活化能数值（185.20、194.19、170.47 kJ/mol）基本一致，因此，进行单组分反应计算时DAEM 方法可以用等转化率法代替。

本研究使用四组分DAEM 法求得的三种生物质中CNT3 和CNT4 的活化能明显高于使用等转化率法求得的平均活化能，Tibola 等[46]使用IPRM法同样发现存在两个高于平均活化能的虚拟组分，说明多组分动力学模型可以提供生物质中活化能较高且在高温下进行分解组分的动力学信息，弥补了单组分动力学模型的缺陷，解释了使用Friedman 法和FWO 法计算时拟合效果随着转化率增加逐渐变差的原因。相比于Soria 等[47]的研究，Guo 等[48]采用双组分DAEM 法将微藻热解反应进行了更全面的描述。Xavier 等[32]的研究中，IPRM 法求得各虚拟组分的峰面积比例ci与升温速率的变化无关，仅与虚拟组分对应的实际组分含量有关，但是Martinez 等[49]采用DAEM 法计算发现，升温速率将会改变半纤维素以及纤维素的峰面积以及峰重叠程度，使生物质DTG 曲线峰型发生变化，结果更加符合实验规律，由此可见，针对多组分反应的动力学分析应该更多的以DAEM法为基础开展。此外，本研究采用模式搜索法对DAEM 法进行改进，减少人为因素影响，与Tibola等[46]和Vamvuka 等[45]使用IPRM 法以及模型配合法相比，所得结果具有更好的客观准确性。

3 结 论

采用Friedman 法与FWO 对热解动力学参数进行计算，杏壳平均活化能为188.22、178.56 kJ/mol，小麦秸秆平均活化能为220.77、200.51 kJ/mol，杨树木屑平均活化能为175.87、174.69 kJ/mol，反应平均活化能整体表现为小麦秸秆＞杏壳＞杨树木屑的规律，三种生物质的活化能最大值均在转化率约为0.4 时出现。

采用DAEM 法从原料组分角度进行计算，结果表明，提取物组分反应平均活化能较高，杏壳、秸秆、木屑分别为287.44 、284.35 与309.96 kJ/mol，各组分活化能存在木质素＜半纤维素＜纤维素＜提取物的关系。三种生物质中半纤维素与纤维素的活化能存在小麦秸秆（128.66、237.47）＜杏壳（131.12、248.23 kJ/mol）＜杨树木屑（137.39、256.09 kJ/mol）的规律。

三种典型生物质的热解活化能与前人研究具有较好的一致性，等转化率法比DAEM 法更易对热解反应整体动力学参数进行初步分析，视为单组分反应时可以替代DAEM 法进行使用，而DAEM法能够与生物质各组分的反应行为进行较好关联，可准确揭示生物质中多组分的复杂热解反应行为，两种方法互相补充可以更加全面地描述农林生物质的热解反应。