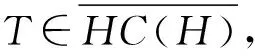有界线性算子的(UWΠ)性质及亚循环性

赵巨涛, 曹小红

(1. 长治学院 数学系, 山西 长治 046011; 2. 陕西师范大学 数学与统计学院, 西安 710119)

1 引言与预备知识

Weyl[1]研究表明, Hilbert空间中自伴算子的Weyl谱恰好等于该算子的谱集除去有限重的孤立特征值, 该结论称为Weyl定理.之后, 许多数学工作者对Weyl定理进行了变型和推广[2-4].(UWΠ)性质[5]是Weyl定理的一种变型, 关于该性质的研究目前得到广泛关注[6-8].本文利用新的谱集, 讨论算子或者算子函数的(UWΠ)性质与亚循环性之间的关系.

令ρea(T)={λ∈:T-λI为上半Fredholm算子且ind(T-λI)≤0},ρSF+(T)={λ∈:T-λI为上半Fredholm算子},σea(T)=ρea(T)称为算子T∈B(H)的本质逼近点谱.可以证明σea(T)⊆[σw(T)∩σa(T)].记ρ(T)=σ(T),ρw(T)=σw(T),ρb(T)=σb(T),σ0(T)=σ(T)σb(T).对集合E⊆, 用isoE,accE和intE分别表示E中孤立点的全体、E聚点的全体及E内点的全体.

2 主要结果

对T∈B(H), 若

σa(T)σea(T)=PD(T),

则称T满足(UWΠ)性质[5], 记作T∈(UWΠ), 其中PD(T)=σ(T)σD(T).

令T∈B(H), 对x∈H,x在T下的轨道定义为

Orb(T,x)={x,Tx,T2x,…}.

1)σw(T)∪∂D连通;

2)σ0(T)=σ(T)σb(T)=Ø;

3) ∀λ∈ρSF(T), ind(T-λI)≥0.

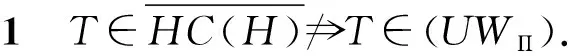
例1设A,B∈B(l2)定义为

A(x1,x2,x3,…)=(x2,x3,x4,…),B(x1,x2,x3,…)=(0,x1,x2,x3,…).

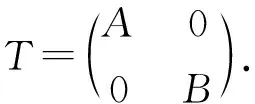
σa(T)=D,σea(T)=∂D,PD(T)=Ø,

于是T∉(UWΠ).

例2设T∈B(l2)定义为

T(x1,x2,x3,…)=(0,x1,x2,x3,…),

例3设A,B∈B(l2)定义为

A(x1,x2,x3,…)=(0,x1,x2,x3,…),B(x1,x2,x3,…)=(0,x2,x3,x4,…),

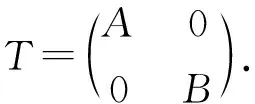
σa(T)={0}∪{λ∈: |λ|=1},σea(T)={λ∈: |λ|=1},PD(T)=Ø,

σa(T)=σea(T)=σ(T)=σw(T)=σb(T),PD(T)=Ø.

下面讨论这两种性质同时成立的条件, 为此先定义一个新的谱集, 令

记σ1(T)=ρ1(T), 则显然σ1(T)⊆σw(T)⊆σb(T)⊆σ(T).

若T∈(UWΠ), 则ρ1(T)⊆ρ(T)∪ isoσ(T).事实上, 若λ0∈ρ1(T), 则存在>0, 使得当0<|μ-λ0|<时,T-μI为Weyl算子, 且

由于T∈(UWΠ), 则T-μI为Browder算子.设asc(T-μI)=p, 则由文献[14]中引理3.4知,

于是当0<|μ-λ0|<时,T-μI可逆.从而λ0∈ρ(T)∪ isoσ(T).

σ(T)=[accσ1(T)∩σea(T)]∪accisoσ(T)∪{λ∈isoσ(T): des(T-λI)=∞},

且σ(T)∪∂D连通.

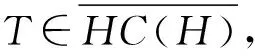
σ(T)⊇[accσ1(T)∩σea(T)]∪accisoσ(T)∪{λ∈isoσ(T): des(T-λI)=∞}

显然成立.对于反包含, 设

λ0∉[accσ1(T)∩σea(T)]∪accisoσ(T)∪{λ∈isoσ(T): des(T-λI)=∞}.

由σea(T)=σ(T)知, accσ1(T)∩σea(T)=accσ1(T).从而必有λ0∉accσ1(T).于是存在>0, 使得当0<|λ-λ0|<时,λ∈ρ1(T).故λ∈ρ(T)∪ isoσ(T).由于λ0∉accisoσ(T), 故可知λ0∈isoσ(T)∪ρ(T).若λ0∈isoσ(T), 则利用λ0∉{λ∈isoσ(T): des(T-λI)=∞}知des(T-λ0I)<∞.于是由文献[15]中定理2.6知,T-λ0I为Drazin可逆的, 即λ0∈PD(T), 与PD(T)=Ø矛盾.因此可得λ0∈ρ(T), 即λ0∉σ(T).

反之, 先证明T∈(UWΠ).根据半Fredholm算子摄动定理[15]可知,

ρSF(T)∩[accisoσ(T)∪{λ∈isoσ(T): des(T-λI)=∞}]=Ø,

于是

因此

[σa(T)σea(T)]∩σ(T)=[σa(T)σea(T)]=Ø.

同理易见

PD(T)∩{[accσ1(T)∩σea(T)]∪accisoσ(T)∪{λ∈isoσ(T): des(T-λI)=∞}}=Ø,

于是σa(T)σea(T)=PD(T), 即T∈(UWΠ).

σ0(T)∩{[accσ1(T)∩σea(T)]∪accisoσ(T)∪{λ∈isoσ(T): des(T-λI)=∞}}=Ø

知,σ0(T)=σ0(T)∩σ(T)=Ø.同理可证明σw(T)=σ(T), 于是σw(T)∪∂D连通.又由

例5令T∈B(l2)定义为

T(x1,x2,x3,…)=(x2,x3,x4,…),

σ(T)=D, accisoσ(T)∪{λ∈isoσ(T): des(T-λI)=∞}=Ø.

于是

σ(T)≠accisoσ(T)∪{λ∈isoσ(T): des(T-λI)=∞},

即[accσ1(T)∩σea(T)]不可缺.

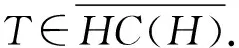
σ(T)≠[accσ1(T)∩σea(T)]∪{λ∈isoσ(T): des(T-λI)=∞},

即accisoσ(T)不可缺.

例8令A,T∈B(l2)定义为

则σ(T)=σea(T)∪accisoσ(T)∪{λ∈isoσ(T): des(T-λI)=∞}且σ(T)∪∂D, 但T∉(UWΠ).

由文献[15]中定理2.6知,

∂σ(T)∩{λ∈: des(T-λI)<∞}⊆PD(T),

故当PD(T)=Ø时, ∂σ(T)∩{λ∈: des(T-λI)<∞}=Ø.又由于accisoσ(T)⊆∂σ(T), 从而accisoσ(T)∩{λ∈: des(T-λI)<∞}=Ø.于是当PD(T)=Ø时, accisoσ(T)⊆{λ∈∂σ(T): des(T-λI)=∞}.从而当T∈(UWΠ)且时, 由定理1知,

σ(T)=[accσ1(T)∩σea(T)]∪{λ∈∂σ(T): des(T-λI)=∞}.

根据半Fredholm算子的摄动定理可知,

ρSF(T)∩∂σ(T)⊆ρb(T)⊆{λ∈: des(T-λI)<∞}.

在定理1或推论1中, 利用包含关系intσ1(T)⊆accσ1(T), 将accσ1(T)改为intσ1(T), 同理可证下列结论, 即下列叙述等价:

2)σ(T)=[intσ1(T)∩σea(T)]∪accisoσ(T)∪{λ∈isoσ(T): des(T-λI)=∞}, 且σ(T)∪∂D连通;

3)σ(T)=[intσ1(T)∩σea(T)]∪{λ∈∂σ(T): des(T-λI)=∞}, 且σ(T)∪∂D连通.

下面用H(σ(T))表示在σ(T)的一个邻域上解析, 并且在σ(T)的任一分支上不为常值的函数的全体.

若σ(T)=[accσ1(T)∩σea(T)]∪accisoσ(T)∪{λ∈isoσ(T): des(T-λI)=∞}或者σ(T)=[accσ1(T)∩σea(T)]∪{λ∈∂σ(T): des(T-λI)=∞}, 则由定理1的证明可知,

σa(T)=σea(T)=σ(T)=σw(T),PD(T)=σ0(T)=Ø，

且任给λ∈ρSF(T), ind(T-λI)≥0.由半Fredholm算子指标的特点可知, 此时对于算子T,σw(·)满足谱映射定理[2].类似文献[2]中定理5可证, 此刻σea(·)也满足谱映射定理.于是任给f∈H(σ(T)),

PD(f(T))=σ0(f(T))=Ø且σa(f(T))=f(σa(T))=f(σea(T))=σea(f(T)),

从而f(T)∈(UWΠ).再利用指标的特点可知, 任给f∈H(σ(T))及任给μ∈ρSF(f(T)), ind(f(T)-μI)≥ 0.从而可得下列结论.

推论3设σ(T)=[accσ1(T)∩σea(T)]∪accisoσ(T)∪{λ∈isoσ(T): des(T-λI)=∞}或者σ(T)=[accσ1(T)∩σea(T)]∪{λ∈∂σ(T): des(T-λI)=∞}连通.若f∈H(σ(T)), 且存在λ0∈σ(T), 使得|f(λ0)|≠0, 则存在c∈, 使得且f(T)∈(UWΠ).

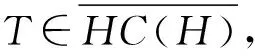
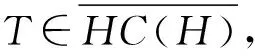
1)T∈(UWΠ);

2)σ(T)=accσ1(T)∪accisoσ(T)∪{λ∈isoσ(T): des(T-λI)=∞};

3)σ(T)=accσ1(T)∪{λ∈∂σ(T): des(T-λI)=∞};

4)σ(T)=intσ1(T)∪{λ∈∂σ(T): des(T-λI)=∞}.

定理2设T∈B(H), 则任给f∈H(σ(T)),f(T)∈(UWΠ)当且仅当下列结论之一成立:

1)σa(T)=[accσ1(T)∩σea(T)]∪accisoσ(T)∪{λ∈isoσ(T): des(T-λI)=∞}, 且任给λ,μ∈ρSF+(T), ind(T-λI)·ind(T-μI)≥0;

2)σb(T)=[accσ1(T)∩σea(T)]∪accisoσ(T)∪{λ∈isoσ(T): des(T-λI)=∞}.

证明: 充分性.设结论1)成立.由

σa(T)=[accσ1(T)∩σea(T)]∪accisoσ(T)∪{λ∈isoσ(T): des(T-λI)=∞}

可证得σa(T)=σea(T),PD(T)=Ø.任给f∈H(σ(T)), 根据PD(f(T))⊆f(PD(T))知PD(f(T))=Ø.又由半Fredholm算子指标的特点知,σea(·)满足谱映射定理, 即任给f∈H(σ(T)),σea(f(T))=f(σea(T)), 于是σea(f(T))=f(σea(T))=f(σa(T))=σa(f(T)).从而任给f∈H(σ(T), 有f(T)∈(UWΠ).

设结论2)成立.由于

[σea(T)]∩{[accσ1(T)∩σea(T)]∪accisoσ(T)∪{λ∈isoσ(T): des(T-λI)=∞}}=Ø,

PD(T)∩{[accσ1(T)∩σea(T)]∪accisoσ(T)∪{λ∈isoσ(T): des(T-λI)=∞}}=Ø,

则

σea(T)=σb(T),PD(T)⊆σ0(T).

又由于

从而

{λ∈ρSF(T): ind(T-λI)<0}∩σb(T)=Ø.

但由于{λ∈ρSF(T): ind(T-λI)<0}⊆σb(T), 故{λ∈ρSF(T): ind(T-λI)<0}=Ø, 即任给λ∈ρSF(T), 有ind(T-λI)≥0.

设f∈H(σ(T)), 并设

μ0∈σa(f(T))σea(f(T)).

反之, 令μ0∈PD(f(T)), 且令f(T)-μ0I=(T-λ1I)n1(T-λ2I)n2…(T-λkI)nkg(T), 其中λi≠λj(i≠j),g(T)可逆.不失一般性, 不妨设任给λi(1≤i≤k),λi∈σ(T), 由于Drazin谱满足谱映射定理, 于是任给λi(1≤i≤k),λi∈PD(T).又由于PD(T)=σ0(T), 于是任给1≤i≤k,T-λiI为Browder算子.从而f(T)-μ0I为Browder算子, 即μ0∈σa(f(T))σea(f(T)).于是再次证明了f(T)满足(UWΠ)性质.

必要性.此时显然T∈(UWΠ).首先可断言: 任给λ,μ∈ρSF+(T), ind(T-λI)·ind(T-μI)≥0.事实上, 若存在λ0,μ0∈ρSF+(T), 使得ind(T-λ0I)=n>0, ind(T-μI)=-m<0.则n必为有限正整数,m为正整数或者+∞.若m有限, 则定义f0(T)=(T-λ0I)m(T-μ0I)n, 否则设f0(T)=(T-λ0I)(T-μ0I).从而0∈σa(f0(T))σea(f0(T)).由于f0(T)∈(UWΠ), 则f0(T)为Browder算子, 于是T-λ0I和T-μ0I均为Browder算子, 与ind(T-λ0I)=n>0, ind(T-μI)=-m<0矛盾.所以断言成立.

下面分两种情形讨论.

情形1) 设σ0(T)=Ø.下面证结论1)必成立.

此时由T∈(UWΠ)知,σa(T)=σea(T),PD(T)=Ø.包含关系σa(T)⊇[accσ1(T)∩σea(T)]∪accisoσ(T)∪{λ∈isoσ(T): des(T-λI)=∞}显然成立.反之, 设λ0∉{[accσ1(T)∩σea(T)]∪accisoσ(T)∪{λ∈isoσ(T): des(T-λI)=∞}}.若λ0∉σea(T), 则λ0∉σa(T).下设λ0∉accσ1(T).类似于定理1的证明可知,λ0∈PD(T)∪ρ(T).由于PD(T)=Ø, 则λ0∈ρ(T), 于是λ0∉σa(T).

情形2) 设σ0(T)≠Ø.下面证结论2)必成立.

首先可断言:σb(T)=σea(T).

事实上, 设λ0∉σea(T), 取μ0∈σ0(T).令f(T)=(T-λ0I)(T-μ0I), 则0∈σa(f(T))σea(f(T)).由于f(T)满足(UWΠ)性质, 于是f(T)为Browder算子, 从而T-λ0I为Browder算子, 即得σb(T)⊆σea(T).反包含显然成立, 于是σb(T)=σea(T).

类似于定理1可知,

σb(T)⊆{accσ1(T)∪accisoσ(T)∪{λ∈isoσ(T): des(T-λI)=∞}}.

又由于σb(T)=σea(T), 于是

σb(T)⊆[accσ1(T)∩σea(T)]∪accisoσ(T)∪{λ∈isoσ(T): des(T-λI)=∞}.

反包含显然成立.故结论2)成立.证毕.

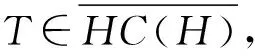
1) 任给f∈H(σ(T)),f(T)∈(UWΠ);

2)σ(T)=accσ1(T)∪ accisoσ(T)∪{λ∈isoσ(T): des(T-λI)=∞};

3)σ(T)=accσ1(T)∪{λ∈∂σ(T): des(T-λI)=∞};

4)σ(T)=intσ1(T)∪{λ∈∂σ(T): des(T-λI)=∞};

5)T∈(UWΠ).

必要性.由定理1显然可得.证毕.

结合定理1, 可得下列结论.

推论7设T∈B(H), 则下列叙述等价:

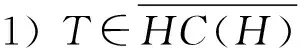
3)σ(T)=accσ1(T)∪ accisoσ(T)∪{λ∈isoσ(T): des(T-λI)=∞}, 且σ(T)∪∂D连通;

4)σ(T)=accσ1(T)∪{λ∈∂σ(T): des(T-λI)=∞}, 且σ(T)∪∂D连通;

5)σ(T)=intσ1(T)∪{λ∈∂σ(T): des(T-λI)=∞}, 且σ(T)∪∂D连通.

若任给x∈H, 有‖T*x‖2≤‖T2x‖·‖x‖, 则T∈B(H)称为*-paranormal算子， 其中T*表示T的共轭算子.若任给λ∈,T-λI均为*-paranormal算子, 则T∈B(H)称为完全*-paranormal算子.

对完全*-paranormal算子T, ∀λ∈,T-λI均有有限的升标.于是当T为完全*-paranormal算子时, 有下列性质: ∀λ∈ρSF+(T), ind(T-λI)≤0.

若T的共轭算子T*为完全*-paranormal算子, 则σea(T)=σb(T),σa(T)=σ(T).于是

accσ1(T)∩σea(T)=accσ1(T),σa(T)σea(T)⊆PD(T),

且任给λ∈ρSF(T), 均有ind(T-λI)≥0.于是有:

推论9若算子T*∈B(H)为完全*-paranormal算子, 则任给f∈H(σ(T)),f(T)∈(UWΠ)当且仅当下列结论之一成立:

1)σ(T)=accσ1(T)∪accisoσ(T)∪{λ∈isoσ(T): des(T-λI)=∞};

2)σb(T)=accσ1(T)∪accisoσ(T)∪{λ∈isoσ(T): des(T-λI)=∞}.