完全二部图的点被多重集可区别的IE-全染色及一般全染色
陈祥恩, 王勇军
(西北师范大学 数学与统计学院, 兰州 730070)
图的点可区别一般边染色由文献[1]提出; 文献[2]引入了图的点可区别一般全染色的概念, 并且研究了路、 圈、 星(即K1,n)、 双星、 三星、 轮、 扇和完全图的一般点可区别全染色, 确定了它们的一般点可区别全色数; 文献[3-6]研究了图的点可区别(被非多重集)IE-全染色, 并考虑了完全三部图; 文献[7-8]研究了圈的点可区别(被非多重集)Ⅰ-全染色及Ⅵ-全染色.本文考虑点被多重集可区别的IE-全染色及点被多重集可区别的一般全染色, 研究完全二部图的点被多重集可区别的IE-全染色及点被多重集可区别的一般全染色, 并确定完全二部图Km,n的点被多重集可区别的IE-全色数及点被多重集可区别的一般全色数.
1 预备知识
图G的一般全染色是指若干种颜色对于图G的全体顶点及边的一个分配.图G使用了k种颜色的一般全染色称为图G的k-一般全染色.图G的IE-全染色是指使得相邻顶点染以不同颜色的一个一般全染色.图G使用k种颜色的IE-全染色称为图G的k-IE-全染色.



从n个互不相同元素中取出r个元素构成的重复组合称为r-组合.r-组合是前述n个互不相同元素构成的集合中含有r个元素的多重子集合, 所以r-组合也称为r-多重子集或r-子集.通常情况下, 进行染色时所用的k种颜色用1,2,…,k表示, 且数字代表的颜色之间有大小关系.本文约定r-子集中的元素按照不减顺序排列.
2 完全二部图的点被多重集可区别的IE-全染色
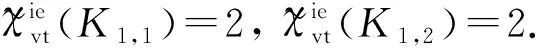
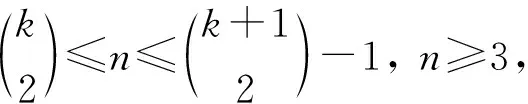



综上可得K1,n的点被多重集可区别的k-IE-全染色.证毕.

当m>2时,m+2<2m, 两种颜色的(m+2)个(m+1)-子集不能区别所有顶点.所以Km,m不存在点被多重集可区别的2-IE-全染色.
下面说明诸ui的色集合各不相同.由染色方案可知, 随着i的增大,ui的色集合中颜色2的个数严格增多, 故诸ui的色集合也各不相同.从而得到了Km,m的点被多重集可区别的3-IE-全染色.
下面利用矩阵更清晰地展示染色方案, 给出一个m+1行、m+1列的矩阵:

该矩阵中第1行元素除0外恰好是u1,u2,…,um的颜色, 第1列元素除0外恰好是v1,v2,…,vm的颜色, 第j行、 第i列相交处的元素恰好是边ui-1vj-1的颜色,i,j≥2.因此第j行元素恰好构成vj-1的色集合, 矩阵的第i列恰好构成ui-1的色集合,i,j≥2.

下面说明诸ui的色集合各不相同.由染色方案可知, 随着i的增大,ui的色集合中颜色2的个数严格增多, 故诸ui的色集合也各不相同.从而得到了Km,m+1的点被多重集可区别的2-IE-全染色.
下面利用矩阵更清晰地展示染色方案, 给出一个m+2行、m+1列的矩阵:

该矩阵第1行元素除0外恰好是u1,u2,…,um的颜色, 第1列元素除0外恰好是v1,v2,…,vm+1的颜色, 第j行、 第i列相交处的元素恰好是边ui-1vj-1的颜色,i,j≥2.因此, 矩阵的第j行元素恰好构成vj-1的色集合, 矩阵的第i列元素恰好构成ui-1的色集合,i,j≥2.

证明: 先证明Km,n不存在使用了(k-1)种色的点被多重集可区别的IE-全染色.


下面构造使用k种色的点被多重集可区别的IE-全染色f.将{1,2,…,k}的所有(m+1)-子集(多重集)排成一个序列, 并使前(m+1)个(m+1)-子集分别是{1,1,1,…,1,1,1},{1,1,1,…,1,1,2},{1,1,1,…,1,2,2},…,{1,2,2,…,2,2,2}.令该序列的前n个子集依次对应顶点v1,v2,…,vn.给顶点vj染对应于它的(m+1)-子集中的第1个元素(颜色), 边uivj染对应于vj的(m+1)-子集中的第(i+1)个元素(颜色), 顶点ui染颜色k,i=1,2,…,m,j=1,2,…,n.此时, 所得染色是IE-全染色,vj的色集合恰好是对应于vj的(m+1)-子集, 因此,v1,v2,…,vm的色集合各不相同,vj与ui的色集合也不相同, 因为vj与ui的色集合中元素个数不同,i,j=1,2,…,m.从而得到了Km,n的点被多重集可区别的k-IE-全染色.



该矩阵第1行元素除0外恰好是u1,u2,…,um的颜色, 第1列元素除0外恰好是v1,v2,…,vn的颜色, 第j行、 第i列相交处的元素恰好是边ui-1vj-1的颜色,i,j≥2.因此矩阵的第j行元素恰好构成vj-1的色集合, 矩阵的第i列元素恰好构成ui-1的色集合,i,j≥2.
3 完全二部图的点被多重集可区别一般全染色
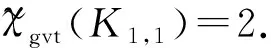
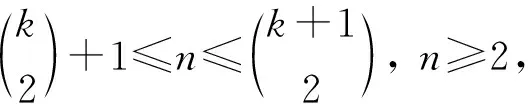


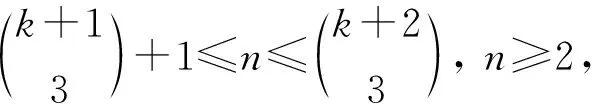
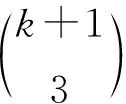

设顶点vj对应的3-子集为{a,b,c},a≤b≤c.令a染点vj,b染边u1vj,c染边u2vj.从而所有2度点以及相关联的边都已染好.最后, 用k染点u1,u2.显然, 每个2度顶点vj的色集合均为事先对应于它的3-子集.度不同的两个顶点的色集合一定不相同.因此在所构造出的染色下, 各顶点的色集合互不相同.于是得到了K2,n的点被多重集可区别的一般全染色.证毕.

下面给出染色方案.令m个(m+1)-子集{1,1,1,…,1,1,1},{1,1,1,…,1,1,2},{1,1,1,…,1,2,2},…,{1,1,2,…,2,2,2}分别对应顶点v1,v2,…,vm.给顶点vj染颜色1, 边uivj染对应于vj的(m+1)-子集中的第(i+1)个元素(颜色), 顶点ui染颜色3,i=1,2,…,m,j=1,2,…,m.此时, 所得染色是一般全染色,vj的色集合恰好是对应于vj的(m+1)-子集, 因此v1,v2,…,vm的色集合各不相同,vj与ui的色集合也不相同, 因为ui的色集合中含3, 而vj的色集合中不含3,i,j=1,2,…,m.
下面说明诸ui的色集合各不相同.由染色方案可知, 随着i的增大,ui的色集合中颜色2的个数严格增多, 故诸ui的色集合也各不相同.从而得到了Km,m的使用了3种颜色的点被多重集可区别的一般全染色.
下面利用矩阵更清晰地展示染色方案, 给出一个m+1行、m+1列的矩阵:

该矩阵第1行元素除0外恰好是u1,u2,…,um的颜色, 第1列元素除0外恰好是v1,v2,…,vm的颜色, 第j行、 第i列相交处的元素恰好是边ui-1vj-1的颜色,i,j≥2.因此, 矩阵的第j行元素恰好构成vj-1的色集合, 矩阵的第i列元素恰好构成ui-1的色集合,i,j≥2.

下面说明诸ui的色集合各不相同.由染色方案可知, 随着i的增大,ui的色集合中颜色2的个数严格增多, 故诸ui的色集合也各不相同.从而得到了Km,m+1的使用2种颜色的点被多重集可区别的一般全染色.
下面利用矩阵更清晰地展示染色方案, 给出一个m+2行、m+1列的矩阵:

该矩阵第1行元素除0外恰好是u1,u2,…,um的颜色, 第1列元素除0外恰好是v1,v2,…,vm+1的颜色, 第j行、 第i列相交处的元素恰好是边ui-1vj-1的颜色.因此, 矩阵的第j行元素恰好构成vj-1的色集合, 矩阵的第i列元素恰好构成ui-1的色集合,i,j≥2.

下面说明诸ui的色集合各不相同.由染色方案可知, 随着i的增大,ui的色集合中颜色2的个数严格增多, 故诸ui的色集合也各不相同.从而得到了Km,m+2的使用2种颜色的点被多重集可区别的一般全染色.
下面利用矩阵更清晰地展示染色方案, 给出一个m+3行、m+1列的矩阵:

该矩阵第1行元素除0外恰好是u1,u2,…,um的颜色, 第1列元素除0外恰好是v1,v2,…,vm+2的颜色, 第j行、 第i列相交处的元素恰好是边ui-1vj-1的颜色,i,j≥2.因此, 矩阵的第j行元素恰好构成vj-1的色集合, 矩阵的第i列元素恰好构成ui-1的色集合,i,j≥2.


下面构造使用k种颜色的点被多重集可区别的一般全染色f.将{1,2,…,k}的所有(m+1)-子集(多重集)排成一个序列, 并使前(m+1)个(m+1)-子集分别是{1,1,1,…,1,1,1},{1,1,1,…,1,1,2},{1,1,1,…,1,2,2},…,{1,2,2,…,2,2,2}.令该序列的前n个子集依次对应顶点v1,v2,…,vn, 给顶点vj染(m+1)-子集中的第一个元素(颜色), 边uivj染对应于vj的(m+1)-子集中的第(i+1)个元素(颜色), 顶点ui染颜色k,i=1,2,…,m,j=1,2,…,n.此时, 所得染色是一般全染色,vj的色集合恰好是对应于vj的(m+1)-子集, 因此,v1,v2,…,vm的色集合各不相同,vj与ui的色集合也不相同, 因为vj与ui的色集合中元素个数不同,i,j=1,2,…,m.从而得到了Km,n的使用了k种颜色的点被多重集可区别的一般全染色.证明诸ui色集合各不相同的方法与定理3相同, 故略.

该矩阵第1行元素除0外恰好是u1,u2,…,um的颜色, 第1列元素除0外恰好是v1,v2,…,vn的颜色, 第j行、 第i列相交处的元素恰好是边ui-1vj-1的颜色,i,j≥2.因此, 矩阵的第j行元素恰好构成vj-1的色集合, 矩阵的第i列元素恰好构成ui-1的色集合,i,j≥2.

