斜投影乘积交换性的一些等价刻画

宋显花, 加羊杰

(1. 青海师范大学 数学与统计学院, 西宁 810008; 2. 青海师范大学 民族师范学院, 西宁 810008)

0 引 言

斜投影(也称幂等元)是结构较简单的算子, 也是最基本的算子, 在系统识别、 系统建模、 多变元分析、 参数估计等领域应用广泛. 目前, 关于斜投影的研究已取得了丰硕的成果[1-11]. 文献[1-4]主要利用算子的值域和零空间研究了两个斜投影乘积的交换性; 文献[5-6]研究了两个斜投影的和、 差、 积等群逆的存在性及其表示形式. 受上述研究工作的启发, 本文利用两个斜投影的和、 差、 积等几种代数组合的{1}-,{1,5}-,{2,5}-逆和群逆给出两个斜投影乘积可交换的等价刻画. 斜投影的其他相关研究可参见文献[7-11].

设B(X)是复Banach空间X上有界线性算子全体构成的集合.设A∈B(X), N(A)和R(A)分别表示算子A的零空间和值域空间,B(H)是复Hilbert空间H上有界线性算子全体构成的集合.设P∈B(X), 若P2=P, 则称P是斜投影.用I(X)表示B(X)上斜投影全体构成的集合.设P∈B(H), 若P2=P=P*, 则称P是投影.用P(H)表示B(H)中投影全体构成的集合,I表示相应空间上的恒等算子.线性算子A∈B(X)的升标和降标分别定义为

asc(A)=inf{p∈: N(Ap)=N(Ap+1)}, dsc(A)=inf{p∈: R(Ap)=R(Ap+1)},

设A∈B(X), 如果存在X∈B(X)满足算子方程(1),(2),(5), 则称A是群可逆算子,X为A的群逆,A的群逆存在当且仅当ind(A)≤1.若A的群逆存在, 则唯一, 记作A#.设B(H)是复Hilbert空间H上有界线性算子全体构成的集合.设A∈B(H),A*表示算子A的伴随算子.如果存在X∈B(H)满足算子方程(1)～(4), 则称A是Moore-Penrose可逆算子,X为A的Moore-Penrose逆.A的Moore-Penrose逆存在当且仅当A的值域是闭的.若A的Moore-Penrose逆存在, 则唯一, 记作A†.对于集合K⊂{1,2,3,4,5}, 如果X∈B(X)或X∈B(H)满足方程(j)(∀j∈K), 则称X是A的K-逆,A的K-逆不一定唯一,A的所有{i,j,…,k}-逆的集合记作A{i,j,…,k}, 其中i,j,…,k∈{1,2,3,4,5}.

1 主要结果

设P,Q∈I(X), 按空间分解X=R(P)N(P), 设

(6)

由Q2=Q知

(7)

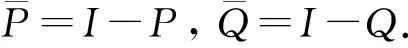
设P,Q∈I(X)如式(6)所示.由

容易验证

(12)

首先, 借助两个斜投影和的{1,5}-逆刻画两个斜投影乘积的交换性.由文献[3] 有

定理1设P,Q∈I(X), 若P+Q的{1,5}-逆存在, 则

其中(P+Q){1,5}表示算子P+Q所有{1,5}-逆的全体之集.

(13)

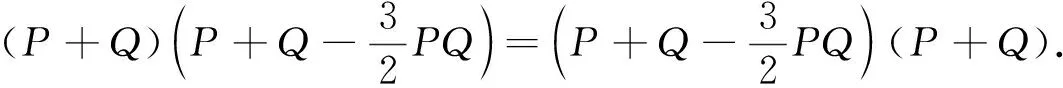
(14)

由式(6),(7)知,

从而由式(8)～(12)知

交换P,Q的位置可得

证毕.

定理1借助P+Q的{1,5}-逆给出了P,Q乘积可交换的充要条件.

注1注意到

因此, 定理1中的{1,5}-逆改成{2,5}-逆时, 结论也成立.

注3若I-PQ的{1,5}-逆存在, 则用与定理1相同的方法可证明PQ=QP⟺I-QP∈(I-PQ){1,5}.

特别地, 当P,Q∈P(H)时, 有PQ=QP⟺PQ∈P(H).于是

定理2若P,Q∈P(H), 则下列条件等价:

1)PQ=QP;

2)P-Q-PQ∈(P-Q){1};

5)I-QP∈(I-PQ){1};

6)P+Q-QP∈(P+Q-PQ){1}.

证明: 1)和2)的等价性由文献[3]中定理4.2可得.由{1}-逆的定义可知,

(15)

(16)

I-QP∈(I-PQ){1}⟺P+Q-QP∈(P+Q-PQ){1}⟺PQP+QPQ=PQ+QP.

(17)

将式(15)右乘P可得

QP=QPQP,

(18)

将式(16)左乘P可得

PQPQPQ+PQPQP=PQ+PQP,

(19)

将式(19)右乘Q可得

2PQPQPQ=PQ+PQPQ,

(20)

由式(19),(20)可得

PQPQ+2PQPQP=PQ+2PQP,

(21)

将式(21)右乘P可得

PQPQP=PQP,

(22)

将式(17)左乘P可得

PQ=PQPQ.

(23)

显然, 式(18),(22),(23)相互等价, 且都等价于PQ=QP.反之, 若PQ=QP, 则式(15)～(17)显然成立.于是1),3),4),5)和6)等价.证毕.

其次, 借助两个斜投影差的群逆刻画两个斜投影乘积的交换性.

此时有

设F=P(P-Q)#,G=(P-Q)#P,H=(P-Q)#(P-Q), 则F,G,H都是斜投影.

定理3设P,Q∈I(X), 若(P-Q)#存在, 则下列条件等价:

1)PQ=QP;

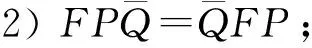
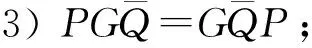
4)QHP=PQH.

证明: 由式(6)和引理1得

(24)

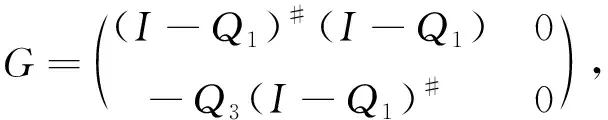
(25)

(26)

再由式(6)及式(24)～(26)知

于是

定理3利用F,G,H这3个斜投影刻画了P,Q乘积的交换性.

最后, 借助两个斜投影乘积的群逆刻画斜投影乘积的交换性.

此时

(27)

(28)

(29)

(30)

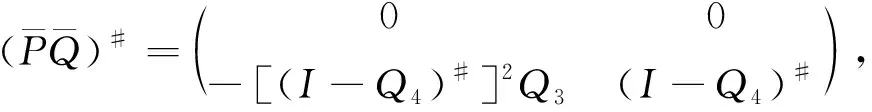
(31)

(32)

证明: 首先, 证明若(PQ)#,(QP)#存在, 则

设P,Q∈I(X)如式(6)所示, 由式(10),(11)知, 只需证明

(PQ)#=Q(QP)#⟺Q1Q2=Q2Q3=Q3Q1=0.

事实上, 有

下面证明式(33)成立⟺Q1Q2=Q2Q3=Q3Q1=0.

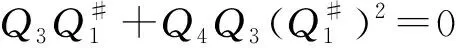
Q2Q3Q1=Q2(Q3Q1+Q4Q3)Q1=0.

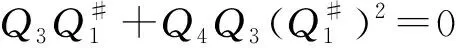
由式(12)知结论成立.证毕.

证明: 只需证明若(PQ)#存在, 则

(34)

设P,Q如式(6)所示, 由式(6),(11),(27)知

(35)

(36)

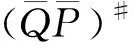
于是由式(12)知结论成立.证毕.