具有恐惧效应和空间异质捕食-食饵模型的稳态解

张萌萌, 李善兵

(西安电子科技大学 数学与统计学院, 西安 710126)

0 引 言

目前, 具有恐惧效应的捕食-食饵模型已得到广泛关注[1-6]. 对于大多数生物物种, 它们生活的自然环境通常是空间异质的. 因此, 除物种之间的直接效应(猎杀)和间接效应(恐惧效应)外, 种群间的动态行为也会受环境异质性的影响. 尽管已有许多数学模型定量研究了恐惧成本在捕食-食饵相互作用中的影响, 但关于空间异质环境中恐惧成本对捕食-食饵模型影响的研究目前文献报道较少[7]. 基于此, 本文考虑一类带恐惧效应和空间异质的Holling Ⅲ型捕食-食饵模型:

(1)

这里:Ω为n中具有光滑边界的有界开区域; Δ为Lapalce算子,u,v分别表示食饵和捕食者的种群密度;du,dv分别表示食饵和捕食者的随机扩散系数; 参数r,k,d,a,m,c均为常数, 其中r>0表示食饵的出生率,d>0表示食饵的自然死亡率,a>0表示食饵的种内竞争,c>0为转化率,k≥0表示恐惧的程度,m∈表示捕食者的自然增长率; 捕食-食饵相互作用系数b(x)>0是空间依赖函数而不是常数.

本文主要讨论恐惧成本和空间异质对系统(1)稳态解的影响, 其中系统(1)的稳态解满足如下非线性椭圆方程:

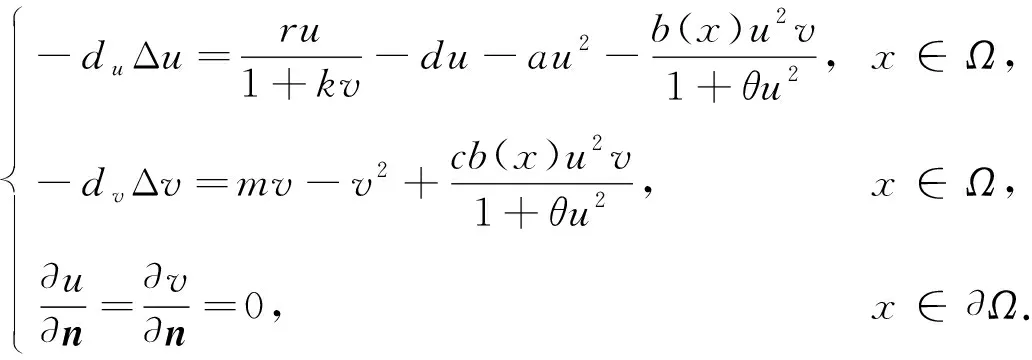
(2)

首先, 利用Riesz-Schauder理论和比较原理分析其平凡解和半平凡解的局部渐近稳定性和全局吸引性; 其次, 利用不动点指数理论建立其正稳态解存在的充分条件.

1 平凡解和半平凡解的稳定性

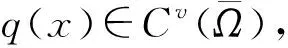
进一步, 关于λ1(d,q(x))有如下性质.

命题1[8-9]下列结论成立:

1)λ1(d,q(x))关于q(x)连续且单调递增, 即当q1(x)≤q2(x)且q1(x)≠q2(x)时,λ1(d,q1(x))<λ1(d,q2(x));

定理1下列结论成立:

1) 当rd或m>0时, (0,0)是不稳定的;

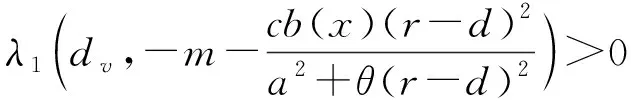
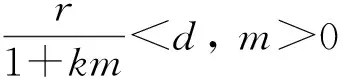
由Riesz-Schauder理论可知, 算子L((r-d)/a,0)的谱点σ(L((r-d)/a,0))由实特征值构成, 且

利用抛物方程的比较原理, 可得如下平凡解和半平凡解的全局吸引性.

定理2下列结论成立:

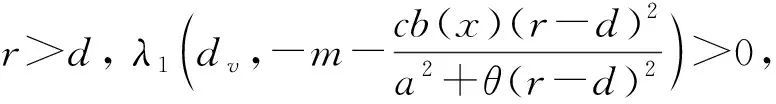
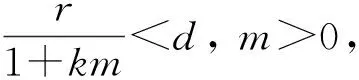
证明: 由于1)～3)的证明类似, 因此这里只给出3)的证明.由系统(1)中v(x,t)的方程可知, 当(x,t)∈Ω×(0,∞)时, 有

设V(x,t)为如下方程的解:

由系统(1)中u(x,t)的方程可知, 当(x,t)∈Ω×[Tε1,∞)时, 有

令U(x,t)为如下方程的解:

再由系统(1)中v(x,t)的方程可得

2 正解的存在性

下面用不动点指数理论, 建立系统(2)正解存在的充分条件.首先给出系统(2)正解的先验估计.

证明: 由系统(2)关于u(x,t)的方程可知,

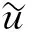
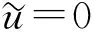
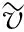
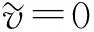
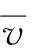
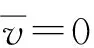
进一步, 当m>0时, 由u(x,t)的方程可知,

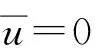
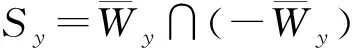
indexW(A,U)=index(A,U,W)=indexW(I-A,U,0),

其中I是一个单位映射, 假设y是 A的一个孤立不动点, 则在W上, A在y处的指标为indexW(A,y)=index(A,U(y),W), 其中U(y)是y在W上的一个小邻域.

假设E=Ey⊕Sy, 其中Ey是E的闭线性子空间,Wy是生成子空间.A在y处的指标可由文献[10](或文献[7])的结果计算.

命题2[10]假设Q:E→Ey是Ey沿着Sy的一个投影算子, 如果L(y)在Wy上没有非零不动点, 则index(A,y)存在, 且下列结论成立:

1) 若Q∘L(y)在Wy上有大于1的特征值, 则indexW(A,y)=0;

2) 若Q∘L(y)在Wy上没有大于1的特征值, 则indexW(A,y)=indexSy(L(y),0)=(-1)σ, 其中σ是L(y)限制在Sy上大于1的特征值的代数重数之和.

对t∈[0,1], 定义一个Fréchet可导紧算子At:D→E如下：

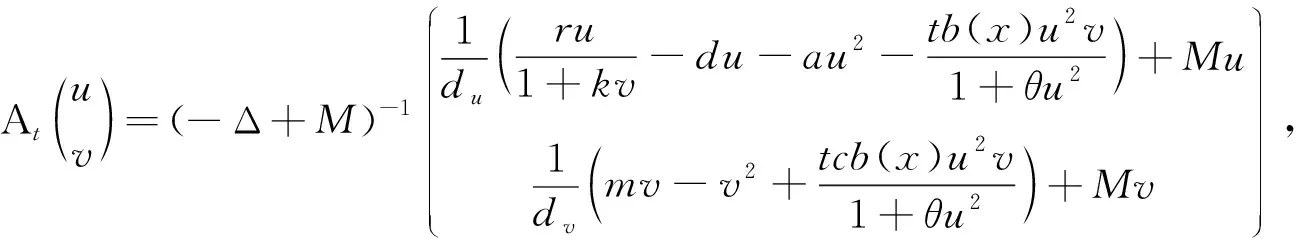
这里M是一个充分大的数, 使得

且

其中(u,v)∈D.

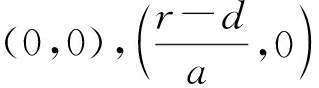
引理2假设r>d,m>0, 则下列结论成立：

1) indexW(A1,(0,0))=0;

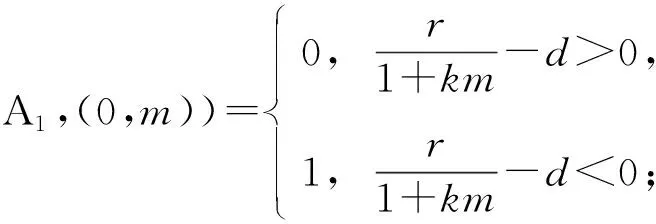
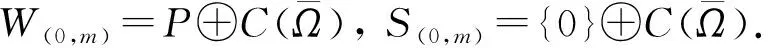
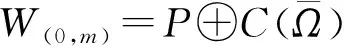
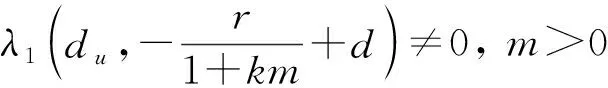
为得到indexW(A1,(0,m)), 下面分析Q∘L1(0,m)的特征值, 其中Q:E→E(0,m)是E(0,m)沿着S(0,m)的投影算子.由Q的定义可知,Q∘L1(0,m)的特征函数都有(φ,0)的形式, 其中φ是以下方程的非零解:

由文献[11]中引理2.4可知, 当λ1(du,-r/(1+km)+d)<0(>0)时,

其中r[L]表示算子L的谱半径.因此, 当λ1(du,-r/(1+km)+d)<0时,Q∘L1(0,m)的特征值大于1, 故indexW(A1,(0,m))=0.另一方面, 如果λ1(du,-r/(1+km)+d)>0, 则Q∘L1(0,m)没有大于1的特征值.因此由命题2知, indexW(A1,(0,m))=(-1)σ, 其中σ是L1(0,m)限制在S(0,m)上大于1的特征值的代数重数之和.下证σ=0.假设(φ,φ)∈S(0,m)是L1(0,m)的特征函数,μ为对应的特征值, 则φ=0,φ是以下方程的非零解:

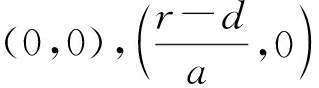
引理3假设r>d,m<0, 则下列结论成立.

1) indexW(A1,(0,0))=0;

3) indexW(A1,D)=1.

借助引理2和引理3, 利用不动点指数的可加性, 可得下列系统(2)正解的存在性.

定理3假设r>d, 则下列结论成立:

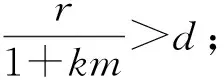
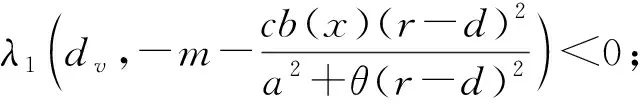
3) 如果m=0, 则系统(2)至少存在一个正解.

1=indexW(A1,D)=indexW(A1,(0,0))+indexW(A1,((r-d)/a,0))+indexW(A1,(0,m))=0,

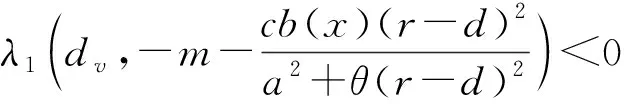
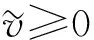
3) 假设(ui,vi)是系统(2)当m=mi时的任一正解, 即(ui,vi)满足

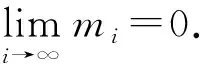
综上, 本文讨论了一类具有恐惧效应和空间异质的捕食-食饵模型的稳态解, 并重点分析了模型平凡解和半平凡解的稳定性以及正解的存在性. 首先利用Riesz-Schauder理论证明了平凡解和半平凡解的局部渐近稳定性. 定理1结果表明, 恐惧效应对半平凡解((r-d)/a,0)的局部稳定性没有影响, 但对半平凡解(0,m)的局部稳定性有明显影响.进一步, 本文利用抛物方程的比较原理得到了平凡解和半平凡解的全局吸引性.定理2结果表明: 当恐惧效应较强时, 半平凡解(0,m)是全局吸引的, 即当恐惧效应较强时, 食饵物种更易灭绝； 同时, 如果捕食者的死亡率过大, 则捕食者无法持久生存, 并最终会灭绝.最后, 借助不动点指数理论建立了模型共存解的存在性.定理3结果表明: 在r>d的条件下, 如果捕食者的自然增长率是正的(i.e.,m>0)且没有恐惧效应(i.e.,k=0), 则模型共存解总是存在的; 但引入恐惧效应后(i.e.,k>0), 只有恐惧效应较弱时, 模型共存解才可能存在, 即恐惧效应对模型共存解的存在性有明显影响.