基于相位幅度耦合的酒精依赖患者ERP脑网络分析

刘兴平 王索刚

1(重庆大学附属三峡医院介入放射诊疗科，重庆 404000)

2(天津医科大学生物医学工程与技术学院，天津 300070)

引言

酒精依赖是一种严重的精神活性物质滥用障碍，全球每年大约有330 万人死于酗酒，约占全世界每年死亡人数的5.9%[1]。 长期的酒精依赖会对大脑造成损伤，影响大脑的执行控制和工作记忆等功能[2]。 酒精依赖极易引发过度吸烟、药物滥用、暴饮暴食等危险行为，尤其是酒后驾驶极大地增加交通事故倾向，容易造成严重的社会影响[3]。 工作记忆是人脑的高级认知功能之一，研究酒精依赖患者的工作记忆任务中的脑电特征，有助于深入了解酒精依赖影响脑功能的潜在机制[4]。

网络神经科学认为，正常大脑是一个复杂且高效的网络，各解剖结构间的高效协作是大脑进行信息处理的工作基础[5]。 在网络分析中，以大脑解剖学部位为网络节点，根据不同节点间的相互作用强度可构建脑网络，并常结合图论进行分析。 基于正电子断层扫描、功能磁共振等技术的结构和功能脑网络研究表明，酒精依赖对于大脑的网络连接有负面影响[6]。 例如，静息态功能磁共振研究表明，慢性饮酒影响大脑的连通性，特别是在左侧执行控制网络[7]。 但是，这些技术采集的信息时间分辨率较低，不能及时反映高速运转的大脑神经动态，而高时间分辨率的事件相关电位(event-related potential，ERP)可及时反映大脑在特定刺激下的神经电生理过程，有助于帮助诊断一些临床特征不明显的疾病，适合于观察酒精依赖患者的脑部活动[8]。 例如，在长期饮酒的青少年的ERP 研究中，发现他们存在与正常青少年不一致的大脑连接和皮质兴奋性变化[9]。 目前，关于酒精依赖患者的ERP 脑网络研究不多，有必要进一步研究，以探讨酒精依赖患者的ERP 脑网络特征。

在脑网络研究中，常通过不同脑区相同节律信号间的相关性、相干性、似然同步性、偏定向相干性等方法，构建特定节律的结构、功能或因果脑网络[6，10]。 近些年交叉节律间的相互关系也得到了广泛关注，因为在脑电中不同节律的神经信息代表着不同信息，通常认为低频信号与大范围脑区间的信息传递有关，而高频信息与局部脑区的信息处理有关，不同脑区间的交叉节律耦合是大脑信息传递和整合的基础[11]。 相位幅度耦合(phase-amplitude coupling，PAC)是低频信号对高频信号进行耦合，会使高频信号幅度在低频信号的相位中分布不均，是被广泛研究的交叉节律耦合类型。 在癫痫、精神分裂症、注意力缺陷多动障碍等多种疾病中，都观察到PAC 的异常变化[11]。 有研究表明，静息态脑电的PAC 可以作为研究酒精依赖的一个定量脑电图指标[12]。 但是，尚未基于PAC 的酒精依赖患者ERP 的脑网络研究。

本研究以开源的酒精依赖患者和健康正常人的ERP 脑电为研究对象，构建交叉导联间的thetagamma、alpha-gamma 耦 合(theta-gamma coupling，TGC；alpha-gamma coupling，AGC)因果网络。 通过进行特定网络密度下的网络图论分析，观察酒精依赖患者与正常人工作记忆中的因果脑网络差异；结合常用频域能量指标，促进对酒精依赖患者ERP 的脑网络特征认识。

1 材料与方法

1.1 数据来源与预处理

ERP 数据来自于美国纽约州立大学提供的开源脑电[13]。 该数据集包含了48 例健康成年人[年龄为(25.81±3.38)岁]和77 例酒精依赖患者[年龄为(35.83±5.33)岁]的61 导联头皮脑电，电极放置使用国际10－20 系统，采样频率256 Hz，电极阻抗小于5 kΩ。 参考电极为鼻尖电极，同时记录水平和垂直眼电。 导联电极位置、编号及脑区分布的图1所示，脑区根据文献[14]分为6 个。 本研究对原始的导联编号进行了重新排列，以使位于相同脑区的导联编号连续。 ERP 使用延迟样本匹配范式(delayed matching-to-sample，DMS)触发:第1 张图片呈现1.6 s 后，显示屏黑屏0.3 s；继而呈现第2 张图片1.6 s，受试者需要对第2 张图片是否与第1 张图片相同做出判断，并在第2 张图片出现时记录时长1 s 的事件相关电位，每个范式间的休息时间为3.2 s。

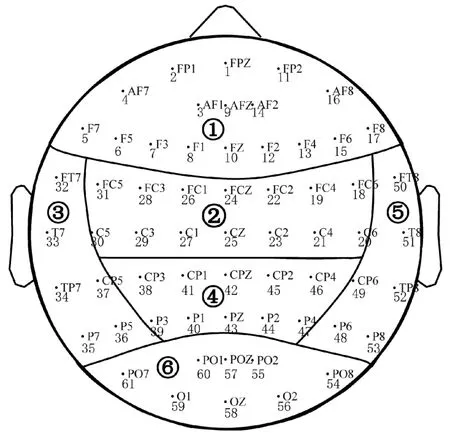
图1 电极位置、编号以及脑区分布(①～⑥分别表示额、中央、左颞、顶、右颞、枕区)Fig.1 Electrodes location， numbering and lobes distribution (①～ ⑥represent the lobe of frontal，central， left temporal， parietal， right temporal and occipital， respectively)

该数据集中包含了健康人和酒精依赖患者在靶刺激(前后两张图片相同)、非靶刺激(前后两张照片不同)两种刺激下的数据，其平均ERP 响应如图2 所示。 在剔除异常较大、有数据缺损的数据后，本研究共计纳入酒精依赖组76 例、健康对照组45例。 使用EEGLAB 工具箱[15]去除50 Hz 工频干扰、肌电、眼电、基线漂移等伪迹，分别对每个受试者同类型的ERP 数据进行叠加平均，以提高信噪比。

图2 叠加平均事件相关电位。 (a) 健康对照组非靶刺激；(b) 酒精依赖组非靶刺激；(c) 健康对照组靶刺激；(d) 酒精依赖组靶刺激Fig.2 Superposition averaging event-related potentials.(a) Non-target stimulation in healthy control group；(b) Non-target stimulation in alcohol-dependent group；(c) Target stimulation in healthy control group； (d)Target stimulation in alcohol-dependent group

1.2 相位幅度耦合强度计算

首先对每个导联所获取的信号进行无相移带通滤波(eegfilt.m)，提取theta(4～8 Hz)、alpha(8～12 Hz)、gamma(30～60 Hz)节律信号。 Berman 等的研究表明，在对幅度信号进行滤波时，其带宽需要使用至少2 倍低频信号高截止频率，以降低检测PAC 的假阴性率[16]。 本研究的gamma 节律带宽范围满足该要求。 对经过带通滤波后的信号，使用希尔伯特变换(hilbert.m)，提取theta、alpha 节律的瞬时相位信息和gamma 节律的瞬时幅度信息，以此计算所有导联对的TGC、AGC 强度。

TGC、AGC 强度计算使用Tort 等从信息学角度提出的PAC 计算方法——调制指数(modulation index，MI)[17]。 以所有导联对间的AGC 强度为例，其计算过程如下:

1)将相位导联的alpha 节律相位([－π， π])均分成Nb等分段。Nb一般为不小于18 的360 的约数，如18、36、72 等，本研究取Nb＝36。

2)计算每个相位段对应的幅度导联gamma 节律的平均幅度。

3)对每一相位段的平均幅度进行归一化，有

式中，n(n＝1， 2， …，Nb)为相位段，Aγ(n)为相位导联alpha 节律相位第n段对应的幅度导联gamma节律的平均幅度值，PA(n)为对应归一化幅度。

4)计算相位幅度分布的Shannon 熵，有

5)MI 为相位幅度分布的归一化Shannon 熵，有

式中，ln(Nb)为最大可能熵，只有当gamma 节律幅度在alpha 节律相位各段中呈现均匀分布时才可能出现。 但是，在复杂的神经电活动中，这种理想化的情况并不存在。 此时，MI 值即为两个导联间的AGC 强度值。

对于61 导联的ERP，将导联分别作为相位导联、幅度导联，计算任意两个导联之间的AGC 强度值，组成61×61 大小的因果连接矩阵，并以矩阵AGC 表示，有

式中，MIi，j表示导联i的alpha 节律相位对导联j的gamma 节律幅度的耦合强度值。

同理，导联对间的TGC 强度值可组成因果连接矩阵TGC。

1.3 脑网络图论分析

根据图论，将61 个导联视为脑网络中的节点，以所有导联对间的耦合强度作为脑网络各节点间连接的边，并设置相同导联的耦合强度值为0；对于每位受试者的ERP 数据，均可由连接矩阵TGC、AGC 构建大小为61×61 的有向权重因果网络。 本研究将计算特征路径长度、平均聚类系数、全局效率、平均局部效率、传递性、直径等6 个脑网络参数，以探讨不同受试、不同工作记忆刺激状态下的因果脑网络差异。

特征路径长度是所有节点间最短路径长度的平均值，是衡量网络整合的网络指标；其值越高，网络功能的整合程度越低。 全局效率是最短路径长度倒数的平均值，与特征路径长度呈负相关的关系。 平均局部效率是基于节点邻域计算的全局效率，是每个节点局部效率的平均值。 平均聚类系数反映了节点与相邻节点的联系紧密程度，是衡量网络分离程度的一个指标，决定了局部信息处理的能力；其值越高，网络功能分离能力越强；因其对每个节点进行了归一化，因此可能会受到低度节点的不均衡影响。 传递性是平均聚类系数的一个经典转换形式，不受节点度不均衡的影响。 网络直径是网络中所有节点间的最长距离，用来衡量网络大小；其值越低，信息传输越快。

在网络图论分析研究中，一般要求网络中所有节点的平均度大于2lnNo≈8.223(No＝61，为网络节点数)，并且网络密度小于0.5，这样可以使网络具有比较好的拓扑特性，因为过高的阈值会导致网络过于稀疏，而过低的阈值会导致网络过于稠密[18]。本研究根据以上两个条件，选取网络密度为0.3 时的阈值化网络来计算网络参数，以保证所有受试者的阈值化TGC、AGC 网络具有同样的连接数目，从而使阈值化网络能够充分反映同样的连接数目下个体间的网络拓扑组织特性差异，而不是由网络连接强度所引起的网络特性差异。 本研究的有向权重网络图论指标使用BCT 工具箱进行计算[19]。

1.4 频域能量指标

通过对脑电进行5 层小波包分解(小波基函数为db5)，计算theta、alpha、beta(12～28 Hz)节律的绝对能量。 此外，本研究还计算了gamma 节律的绝对能量。 吴绍斌等提出可以反映个体疲劳程度的疲劳因子R[20]，R值越大，疲劳程度越强，其计算如下。

式中，Eθ、Eα、Eβ分别为theta、alpha、beta 节律的绝对能量。

1.5 统计学分析

统计学分析在SPSS 24.0 中进行。 Shapiro-Wilk检验结果显示，数据不满足正态性，数据以四分位数表示50%(25%， 75%)。 两组间相同或不同刺激条件下的数据差异检验使用非参数Mann-Whitney U检验，同组不同刺激条件下的数据差异使用Wilcoxon 符号秩检验。 所有导联对的耦合强度值及各节律能量参数的多重比较结果，使用0.05 的伪发现率(false discovery rate，FDR)进行校正。 显著性水平设为0.05。

2 结果

2.1 相位幅度耦合分析

对健康对照组和酒精依赖组导联对的TGC、AGC 强度进行比较(组内靶刺激与非靶刺激比较，组间靶刺激及组间非靶刺激比较)，结果显示:仅在非靶刺激下，健康对照组与酒精依赖组的TGC、AGC强度存在具有显著差异的导联对(TGC 中占比15.29%，AGC 中占比1.29%，FDR 校正均P<0.05，见图3)，而其他的耦合强度比较则导联对耦合强度差异无统计学意义(FDR 校正均P>0.05)。 图3(a)、(b)中的黑色线对应图1 中的脑区划分，图3(a)中的数据使用两组内平均值的差值(健康对照组－酒精依赖组)进行表示，图3(b)为检验结果统计量Z值。 图3(c)为两组间差异具有统计学意义的导联对分布情况(FDR 校正均P<0.05)，导联对间的连线箭头起始段表示该导联为theta 或alpha 相位提供导联，箭头末端为gamma 幅度提供导联；导联点颜色为灰色，表示差异无统计学意义；导联点或导联对彩色，表示FDR 校正后P<0.05。 图3(d)中，小提琴图内黑色横虚线从下到上，分别为组内数据的25%、50%、75%百分位数。

图3 相位幅度耦合强度对比(第1、2 行分别对应TGC、AGC 网络)。 (a) 交叉导联平均耦合强度差值(健康对照组－酒精依赖组)；(b) Mann-Whitney U 检验Z 值；(c) 组间显著差异导联对分布；(d) 所有导联对平均耦合强度的小提琴图Fig.3 Comparison of phase-amplitude coupling intensity(The first， second row correspond to TGC， AGC networks respectively).(a) The average coupling intensity difference of cross channels (healthy control group －alcohol-dependent group)； (b) The Z value of Mann-Whitney U test； (c) Distribution of paired channels with significant difference between groups； (d) Violin plots of average coupling intensity of all paired channels

在TGC、AGC 强度上，酒精依赖组无显著强于健康对照组的导联对(FDR 校正均P>0.05)，图3(c)显示的均为酒精依赖组显著弱于健康对照组的导联对(FDR 校正均P<0.05)。 图3(a) ～(c)显示，酒精依赖组的TGC、AGC 强度均在多个导联对间减弱，并且在双侧颞、顶、枕区被耦合时较多，其中TGC 的差异更大。 图3(d)关于两组间所有导联对平均耦合强度的比较结果也显示，酒精依赖组所有导联对的TGC、AGC 平均耦合强度[TGC: 0.014(0.011， 0.018) vs 0.012(0.010， 0.014)，P＝0.002； AGC: 0.012 (0.010， 0.014) vs 0.011(0.010，0.012)，P＝0.005]均显著减弱，以TGC 差异更为明显。

以上结果表明，在非靶刺激状态下，酒精依赖患者各脑区间的信息交流存在障碍，并且这种现象以TGC 网络双侧颞区、顶区、枕区等脑区作为信息接收脑区时较为明显。

2.2 脑网络图论分析

图4 为健康对照组和酒精依赖组在网络密度为0.3 时的6 个脑网络特性。 在其中的各小提琴图中，从下到上的3 条黑色横虚线分别表示组内数据的25%、50%、75%百分位数。 与健康对照组相比，TGC 网络中，酒精依赖组的特征路径长度[84.13(60.96， 110.33) vs 104.24(86.93， 118.98)，P＝0.005]、直径[222.40 (154.78， 254.39) vs 253.39(207.82， 307.99)，P＝0.003]均显著增加，平均聚类系数[0.013(0.010， 0.019) vs 0.009(0.008，0.012)，P< 0.001]、全局效率[0.014 (0.011，0.016) vs 0.011(0.010， 0.013)，P<0.001]、平均局部效 率[0.017(0.013， 0.022) vs 0.013(0.011，0.017)，P<0.001]、传递性[0.011(0.008， 0.016) vs 0.008(0.007， 0.010)，P<0.001]均显著降低；AGC网络中，酒精依赖组的特征路径长度[103.40(92.38，122.89) vs 116.95 (104.84， 130.29)，P＝0.018]显著增加，平均聚类系数[0.010(0.008， 0.013) vs 0.008(0.007， 0.010)，P＝0.014]、 全局效率[0.011(0.009， 0.012) vs 0.010(0.009， 0.011)，P＝0.008]、平均局部效率[0.013(0.011， 0.016) vs 0.011(0.010， 0.013)，P＝0.007]、传递性[0.008(0.007，0.010) vs 0.007(0.006，0.008)，P＝0.009]均显著降低，直径[241.26(178.80， 290.34) vs 260.54(218.05， 304.27)，P＝0.135]差异无统计学意义。 这表明，酒精依赖患者的TGC、AGC 脑网络的功能整合、分离能力降低，其大范围脑区间的信息传递可能受阻。

图4 脑网络特性比较。 (a) 特征路径长度；(b) 平均聚类系数；(c) 全局效率；(d) 平均局部效率；(e) 传递性；(f)直径Fig.4 Comparison of brain network characteristics.(a) Characteristic path length； (b) Average clustering coefficient； (c) Global efficiency； (d) Average local efficiency； (e) Transitivity； (f) Diameter

2.3 各节律能量及疲劳因子

比较酒精依赖组与健康对照组各导联的theta、alpha、beta、gamma 节律的绝对能量以及疲劳因子的差异，结果如图5 所示。 与健康对照组相比，酒精依赖组的theta 节律能量在除左额区外的多数导联中显著降低(占95.08%，FDR 校正均P<0.05)，alpha 节律能量在全部导联中均显著降低(占100%，FDR 校正均P<0.05)，beta 节律能量在左侧中央区和右侧顶、枕区显著降低(占50.82%，FDR 校正均P<0.05)，gamma 节律能量在各导联中均差异无统计学意义(FDR 校正均P>0.05)。 疲劳因子的对比结果显示，酒精依赖组在左侧后颞区和右颞区显著降低(占45.90%，FDR 校正均P<0.05)。 这表明，在非靶刺激状态下，酒精依赖患者的低频(theta、alpha)脑电活动向较高的节律(beta)增加，相比健康正常人更为活跃，同时更不易疲劳，呈现亢奋状态。

图5 能量指标比较(第1 行为Mann-Whitney U 检验结果Z 值，第2 行为FDR 校正后的P 值)。 (a) Theta 能量；(b) Alpha 能量；(c) Beta 能量；(d) Gamma 能量；(e) 疲劳因子Fig.5 Comparison of energy(The first row is the Z value of Mann-Whitney U test results， and the second row is the adjusted P value after FDR correction).(a) Theta power； (b) Alpha power； (c) Beta power； (d) Gamma power；(e)Fatigue factor

3 讨论

本研究通过计算交叉导联对的TGC、AGC，构建权重因果脑网络，并结合各节律的小波包能量，对酒精依赖患者和健康对照组在DMS 工作记忆范式中进行非靶刺激时的ERP 进行分析，发现酒精依赖患者存在因果脑网络拓扑组织和多脑区活动的异常。

静息态脑电研究发现，额区和顶区的TGC 显著强于其他脑区对的TGC，但在饮酒后这种耦合效应明显减弱[12]。 本研究结果与之相符，同时还发现酒精依赖患者存在更多脑区及脑区间的TGC 耦合强度降低。 此外，还观察到酒精依赖患者在双侧颞区后部以及顶、枕区等后部脑区，与其他脑区间的TGC、AGC 耦合存在异常，这与Zhang 等[13]发现酒精依赖患者的颞、枕区异常活动相似。

本研究的结果显示，酒精依赖患者的TGC、AGC因果脑网络呈现以下特点:全局效率降低，特征路径长度增加，多脑区间的协调整合能力下降；平均聚类系数、平均局部效率降低，局部脑区的功能分离能力下降；网络直径增加，传递性降低，大脑各脑区间的信息流动速度下降。 Huang 等[21]的研究表明，酒精依赖患者的左半球后扣带皮层接受其他脑区的信息传入受阻，尤其是与左半球背侧前扣带回的连接同步性降低，使得其大脑信息整合能力下降。 此外，Wang 等[22]的研究表明，男性酒精依赖患者的功能网络连通性、全局效率均较低，本研究的结果与之相似。 Sjoerds 等[23]的研究表明，随着酒精依赖患者的患病时间增加，患者脑网络的全局效率和平均聚类系数均逐渐降低，但是他们与健康对照组相比脑拓扑差异并不显著。 本研究的结果显示，二者的因果网络存在显著差异，这可能是脑电数据来源、脑网络的构建方式等不一致导致的。 PAC 是一种神经元相互作用的测量方法，本研究的结果表明酒精依赖患者，表现出功能性神经元系统间的相互作用减弱(TGC、AGC 减弱)，这可能与患者自上而下的抑制控制减弱有关，会进一步导致其脑拓扑组织紊乱，效率降低。

基于同样的数据集，李宁等[24]分析发现，酒精依赖患者的ERP 与健康人的ERP 存在差异，如存在大范围的theta、alpha 节律功率降低，多个脑区的疲劳因子均有大幅度降低，中枢神经系统的抑制减弱，大脑皮层的兴奋性增强。 本研究的结果也显示，在进行非靶刺激时，酒精依赖患者出现大部脑区theta、全局脑区alpha、局部脑区beta 节律能量降低，以及疲劳因子下降，脑活动比较活跃。 这表明，在DMS 工作记忆过程中，酒精依赖患者大脑的抑制控制能力减弱。 推测是在工作记忆的任务态下，大脑的主要节律由静息态的低频节律转向更高频节律，同时酒精依赖患者存在相对健康人更明显的alpha 节律阻断现象，患者的ERP 高频活动更强烈[25-26]。

酒精依赖患者的工作记忆表现相比健康人要差，如DMS 工作记忆范式中错误率更高、反应时间更长等[13]。 本研究中，TGC、AGC 两种网络类型的结果得到相互印证，同时频域能量的分析结果也支持了网络的分析结果，这些结果可为酒精依赖患者工作记忆较差提供合理的解释。 进一步的研究可以考虑使用能够反应瞬时PAC 强度的方法，深入观察在工作记忆过程中脑部活动的动态PAC 变化，促进对于酒精依赖患者脑电特征的认识。 值得一提的是，本研究中的酒精依赖组和健康对照组在靶刺激或者在其组内不同刺激状态下的PAC 强度均无显著差异，PAC 强度并不能很好地区别其ERP 差别，还需要结合其他脑电指标(如信息熵、排列熵等)进行进一步的探究。 此外，后续的研究可以考虑进行机器学习分类分析，以检测所提出的指标用于临床辅助诊断的准确性和可行性。

4 结论

在DMS 工作记忆范式中进行非靶刺激时，酒精依赖患者的ERP 特征与健康正常人存在明显差异。酒精依赖患者高频活动增高、低频活动降低，TGC、AGC 网络存在功能分离、整合能力降低等问题，其脑电活动更为活跃，大脑抑制控制能力减弱，脑网络拓扑组织紊乱。 结合频域能量等脑电指标，TGC、AGC 强度和相关脑网络参数，可提高对酒精依赖导致工作记忆等高级认知功能受损的认识。 本研究为酒精依赖研究提供了一种基于PAC 的定量分析方法，也可为其他疾病的临床诊疗提供理论依据。