基于时变copula互信息的肌间耦合分析

王洪安 佘青山∗ 马玉良 孔万增 田玉平

1(杭州电子科技大学自动化学院(人工智能学院)，杭州 310018)

2(浙江省脑机协同智能重点实验室，杭州 310018)

引言

在人的自主运动过程中，大脑运动皮层以神经元的振荡和同步放电的方式发出运动控制指令，经下行神经通道传递至脊髓，通过募集一组特定的肌肉协同模块，实现对复杂运动任务的最优控制[1]。脑电(electroencephalography， EEG)信号和身体对侧的表面肌电(surface electromyogram， sEMG)信号分别反映了运动控制信息和功能响应信息，脑肌电信号之间带节律的同步特征揭示了运动过程中大脑皮层和相应肌肉之间的功能耦合连接[2]。

研究表明，在中枢神经系统的功能调节和反馈控制下，与运动相关的肌肉之间存在不同时空层次的信息交互和耦合关系[3]。 这种特殊的耦合关系不仅反映了运动过程中肌肉间的相互关联和相互作用，还包含了神经系统对运动肌肉的控制支配作用[4]。 肌间耦合是从皮层肌肉耦合研究中发现并引申而来的，源于特定的运动任务下，相关肌肉的运动神经元共享相同的皮质脊髓驱动[5]。 肌间耦合存在频段显著特征，主要表现为alpha (8～15 Hz)频段的肌间耦合受脊髓神经的控制，影响肌肉的非自主收缩和运动姿势的维持；beta (15～30 Hz)频段的肌间耦合代表了从初级运动皮层到运动神经元的信息传递过程，与静态力的输出有关；gamma(30～60 Hz)频段的肌间耦合受大脑皮质神经的控制，体现为认知过程中注意力集中引发的强烈紧张性收缩[6]。 不同频段的肌间耦合特性，为理解运动控制的组织和协调机制提供了理论依据。 当前，肌间耦合关系的研究集中在运动医学、康复工程等领域，已成为运动神经科学关注的热点问题。

近年来，肌间耦合分析方法层出不穷，相干性(coherence)因其算法原理简单、易于实现，被广泛应用于肌间耦合分析。 谢平等[7]利用相干性，对比分析了中风患者在运动过程中健侧、患侧上肢拮抗肌间的相干性特征，发现患侧在beta 频段的肌间相干性相对于健侧存在明显缺失。 然而，肌间耦合关系也包含非线性成分，基于傅里叶变换的相干性仅能描述线性耦合关系，并且Faes 等[8]指出，相干性所测得的耦合关系包含了直接和间接的影响，会过度估计肌间耦合强度。 概率论和信息论中的互信息(mutual information， MI)是传统相关系数的非线性扩展，不依赖既定模型，能够度量两个或多个随机变量之间的线性或非线性依赖程度，在很多方面被认为是较完美的关联统计工具。 然而，互信息的估计非常依赖概率密度函数的精确表示，这在实际应用中通常十分困难。 Ma 等[9]证明了负的copula熵可以等价为互信息，通过copula 函数估计互信息，不仅能有效避免对联合密度函数的估计，而且计算复杂度低，这为理解和估计互信息提供了一条新的思考途径。

Sklar 定理指出，一个N维联合分布函数可以分解为N个边际分布函数和一个copula 函数[10]。 该copula 函数完整地描述了变量间的相关性，被译为“连接函数”或“相依函数”，在生物统计学、金融风险度量等许多领域都有着重要贡献。 Fisher 等[11]指出，copula 函数的优势突出表现在两个方面:一是可用来构建复杂的高维概率密度；二是copula 函数可以捕捉线性、非线性、对称以及非对称相关性。Copula 函数种类繁多，主要有椭圆copula 函数和阿基米德copula 函数；不同copula 函数结构不同，在实际应用时需要与数据的分布类型很好匹配。 现阶段大部分研究都是基于参数静态的常相关copula函数，这种函数被认为不能反映相关结构的动态变化，具有一定的局限性[12]。 其实，早在2001年Patton 就已提出参数时变的copula 函数[13]，其构造原理类似于一个ARMA (1， 10)过程。 近几年，时变copula 函数因其相关参数时变的特点，在气象、经济等领域取得了较好发展[14-16]。

针对现有的肌间耦合分析方法存在的不足，笔者提出了一种利用时变copula 函数估计互信息的新方法，定量研究了不同特征频段的肌间耦合关系，并在Ninapro DB4 公开数据集上进行了测试和分析，为进一步探索上肢运动功能障碍的产生机理以及运动功能康复评估，提供新的研究方法和理论依据。

1 材料和方法

1.1 时变copula 函数

二元分布的Sklar 定理[10]指出，若二维随机变量x、y的联合分布函数为F，边际分布函数分别为u和v，则存在一个copula 函数C，使得

若u、v连续，则C是唯一的。 这个copula 函数描述了变量间的相关结构。 根据式(1)，可得x、y的联合密度为

式中，c(u，v) 表示copula 密度函数，f(x) 与f(y)分别表示x和y的概率密度函数。

时变copula 函数也称为条件copula 函数，其数学形式和静态copula 函数的形式相同，只有copula函数的参数发生变化[13]。 下面介绍两种常用的时变copula 函数。

1.1.1 时变normal copula 函数

时变normal copula 函数的分布函数表达式为

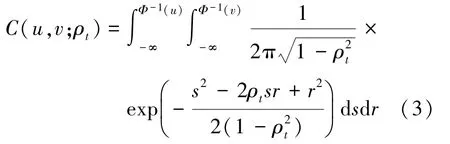
式中，Φ－1(·) 为标准正态分布的逆函数，ρt为时变相关系数。

时变normal copula 函数对尾部相关变化不敏感，即在时变相关系数值域(－1， 1)区间内，上、下尾部的相关系数均为0。

1.1.2 时变SJC copula 函数

时变SJC (symmetrized Joe-Clayton) copula 函数由JC (Joe-Clayton) copula 函数变换而来，其分布函数表达式为

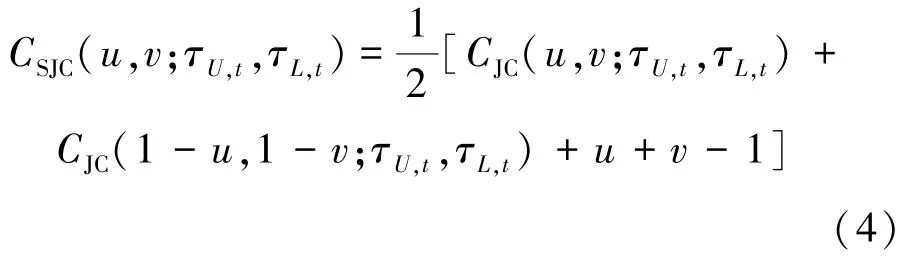
其中

式中，τU，t和τl，t分别为上尾相关系数和下尾相关系数。

时变SJC copula 函数对上、下尾相关变化均敏感，在一定程度上，时变SJC copula 函数的适用范围更广。

1.2 时变copula 互信息

互信息是信息论中的一个基本概念。 与传统的独立性统计度量方法不同，如相关性系数(二阶统计量)和高阶统计量，互信息是全阶次、非线性相关的度量。 Ma 等[9]证明了互信息本质上是一种copula 熵，即

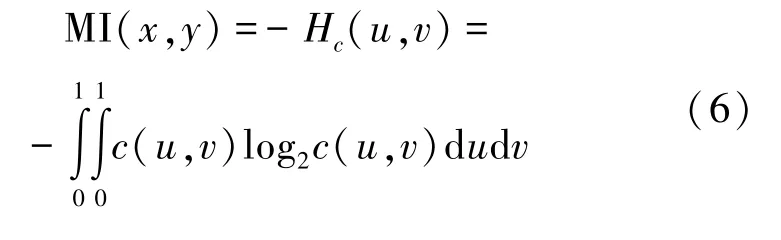
式中，Hc(u，v) 表示随机变量x和y之间的copula 熵。

由式(6)推导的互信息一般称为copula 互信息，它具有连续、对称、可加和对边际分布单调变换不敏感等特质[10]。 Copula 互信息的值越大，表示变量间相互依赖程度越大。

计算copula 互信息的关键，在于边际分布函数的拟合、copula 函数的选择和copula 熵的估计。 其中，copula 函数的选择尤为重要，不同的copula 函数具有不同的表现形式，变量间刻画的相依结构大相径庭，所得的copula 互信息也大小不一。 据此，为更加准确、合理地权衡变量间的耦合关系，本研究提出一种新的时变copula 互信息方法。

首先利用样本的经验分布函数u＾、v＾作为总体边际分布函数的近似，然后根据典型极大似然估计法(canonical maximum likelihood， CML)，估计时变copula 函数中的时变相关参数θ＾n，并将时变copula密度函数ctv代入式(6)中， 进而采用蒙特卡洛法计算copula 熵，最后得到时变copula 互信息。 具体推导过程如下:

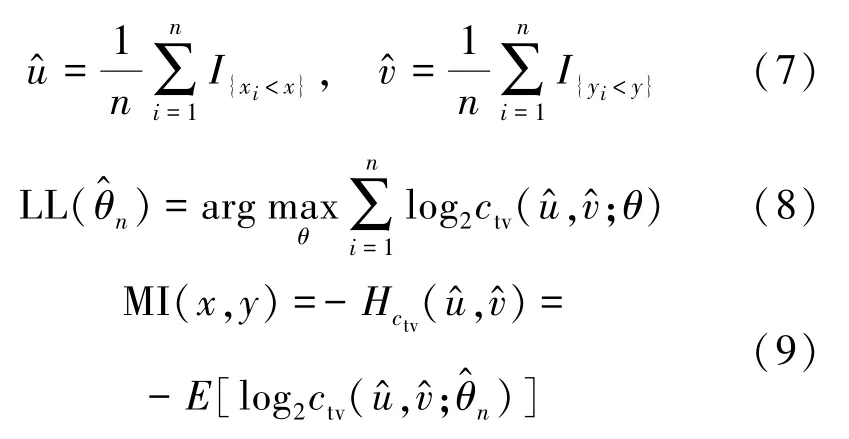
式中，I为示性函数，E[·] 表示求期望，时变copula互信息单位为比特(bit)。

时变copula 函数可通过求偏导得到时变copula密度函数，以时变normal copula 函数为例，其时变copula 密度函数为

1.3 实验数据与分析

使用Ninapro DB4 公开数据库提供的sEMG 数据集(https:/ /doi.org/10.528 1/zenodo.1000138)[17]。 这些数据来自10 名健康受试者(S1～S10)，其详细情况如表1 所示。 每位受试者要求完成52 种手腕、手和手指动作(外加休息)，每种动作重复6 次，每次执行5 s，休息3 s。

表1 受试者的相关信息Tab.1 Demographic information of subjects

数据集中的stimulus 时间序列用于设置每种运动重复片段的起点和终点。 每段由MyoBock 13E200－50 系统(Cometa Wave Plus ＋Dormo)记录的12 通道sEMG 信号组成，采样频率为2 000 Hz，利用均方根进行校正。 12 个无线有源单差分电极的位置分别为:8 个电极(Channel 1～8)均匀分布于前臂周围，与肱桡关节对应；2 个电极(Channel 9～10)，放置在指屈肌和指伸肌的主要活动点上；2 个电极(Channel 11～12)，放置在肱二头肌(BB)和肱三头肌(TB)的主要活动点上。

运动任务主要集中在腕部运动的两个特定的自由度上:腕屈(wrist flexion， WF)和腕展(wrist extension， WE)，如图1 所示。 选取BB 和TB 这两块肌肉作为研究对象。 鉴于sEMG 信号频域特征突出，在不同特征频段上肌间耦合特性存在明显差异，因此本研究利用切比雪夫Ⅱ型带通滤波器，将BB 和TB 的sEMG 信号划分到不同频段上，即theta(4～8 Hz)、alpha (8～15 Hz)、beta (15～30 Hz)和gamma (30～60 Hz)，并且参照文献[18]的做法，将gamma 频段进一步细分为低gamma (30～45 Hz)和高gamma (45～60 Hz)两部分进行实验对比分析。

图1 腕屈和腕展Fig.1 Wrist flexion (WF) and wrist extension (WE)

1.4 方法验证和统计分析

为体现时变copula 互信息在衡量肌间耦合强度方面的能力，首先采用经验分布函数逼近变量的真实分布，并比较了静态normal copula、静态SJC copula、时变normal copula 和时变SJC copula 等4 种不同的copula 函数对不同频段肌间相依关系的拟合情况，这些函数的参数通过极大似然估计法进行确定；再根据赤池信息准则(Akaike information criterion， AIC)，判断不同copula 函数的拟合优度[19]，AIC 值越小表明相应的copula 函数对样本数据的拟合程度越高。 其次，为验证时变copula 互信息度量肌间耦合强度的有效性，选取了上述两种静态copula 函数和两种时变copula 函数去估计互信息，同时进行对比分析，按照AIC 最小原则，从中挑选出拟合效果最佳的时变copula 函数。 最后，利用最适合腕屈(WF)和腕展(WE)的时变copula 互信息，刻画不同动作在不同频段上的肌间耦合强度，并使用独立样本t检验法统计校验，进一步探讨其与被试的生理参数之间的相关性，显著性水平均设为0.05。

2 结果

2.1 静态copula 和时变copula 的性能比较

表2 给出了受试者S8 在第3 次腕屈(WF)、腕展(WE)时，静态copula 函数和时变copula 函数在5个特征频段的AIC 值。 由表2 可见，腕屈运动过程中，除了高gamma 频段以外的其他4 个特征频段，normal copula 的AIC 值都比SJC copula 的要小，在theta 和高gamma 频段，时变SJC copula 的AIC 值要低于时变normal copula 的相应值，而在alpha、beta和低gamma 频段，时变normal copula 的AIC 值要低于时变SJC copula 的相应值；腕展运动过程中，在alpha 和beta 频段，normal copula 的AIC 值要比SJC copula 的相应值小；而在theta 和gamma 频段，SJC copula 的AIC 值要低于normal copula 的相应值。同静态copula 函数的AIC 结果一致，时变copula函数在相应频段亦有此特点。 相比而言，时变copula 函数的AIC 值要明显低于静态copula 函数的相应值。 这说明，在腕屈和腕展的运动过程中，时变copula 函数对肌间相依结构的拟合优度要比静态copula 函数的相应值更高，时变copula 函数对肌间相依结构的刻画要比静态copula 函数相应结构的刻画更合适。

表2 静态和时变copula 函数的AIC 比较Tab.2 Comparison of AIC using static and time-varying copula functions

图2 给出了静态和时变normal copula 函数在5个特征频段的静态相关系数和时变相关系数对比结果。 由图2(a)可以看出，在腕屈运动过程中的不同特征频段上，相比几乎不变且趋近于0 的静态normal copula 相关系数，时变normal copula 相关系数能够反映BB 与TB 随时间变化的动态相关特征，且频段越高时变normal copula 相关系数的变化越剧烈，在总体上表现出正相关的特点；由图2(b)可以看出，在腕展运动过程中的不同特征频段上，静态normal copula 相关系数很低，集中在0 附近，而时变normal copula 相关系数则不尽相同，表现为一种低频段高相关、高频段低相关的特点，从平均结果来看，相关程度并不高。

图2 静态和时变normal copula 函数的相关系数对比。 (a) 腕屈；(b) 腕展Fig.2 Comparison of correlation coefficients of static and time-varying normal copula functions.(a)WF；(b)WE

图3 给出了静态和时变SJC copula 函数在5 个特征频段的静态相关系数和时变相关系数的对比结果。 由图3(a)可以看出，在腕屈运动过程中的不同特征频段上，静态SJC copula 上、下尾相关系数都趋近于0，而时变SJC copula 上、下尾相关系数则明显不同。 较为特别的是，在alpha 和beta 频段，BB和TB 的静态SJC copula 上尾相关系数与时变SJC copula 上尾相关系数保持一致，均为0；在theta 和低gamma 频段，BB 和TB 的静态SJC copula 下尾相关系数与时变SJC copula 下尾相关系数保持一致，均为0；而在其他特征频段，BB 和TB 的时变SJC copula 上、下尾相关系数都比较高，平均值大于0.5，表现为较强的正相关，且频段越高时变SJC copula 上、下尾相关系数的变化越剧烈。 由图3(b)可以看出，在腕展运动过程中不同特征频段上，静态SJC copula 上、下尾相关系数在不同特征频段上都几乎为0，而时变SJC copula 上、下尾相关系数则截然不同(除alpha 和beta 频段的时变SJC copula下尾相关系数)，总体上表现为较高的正相关性，尤其是在低频段；对照来看，高频段的时变SJC copula上、下尾相关系数存在局部峰值(或局部低相关)特点，平均相关程度不如低频段。 图2、3 说明，在腕屈和腕展运动过程中，BB 与TB 在不同特征频段上存在不同的时变相关性，频段差异明显，静态copula相关系数容易错误地低估肌间相关关系。

图3 静态和时变SJC copula 函数的上、下尾部相关系数对比。 (a) 腕屈；(b) 腕展Fig.3 Comparison of upper tail correlation coefficients and lower tail correlation coefficients of static and timevarying SJC copula functions.(a) WF；(b) WE

2.2 基于时变copula 互信息的肌间耦合强度分析

2.2.1 静态与时变copula 互信息的性能比较

仍以受试者S8 为例进行详细说明。 图4 给出了BB 与TB 在5 个特征频段上，静态和时变copula互信息的估计结果。 在腕屈、腕伸运动过程中，BB和TB 在5 个特征频段上，时变copula 互信息均要明显高于静态copula 互信息。 具体表现为:在theta、alpha、beta 和 低gamma 频 段，时 变normal copula 互信息要高于其他copula 互信息；而在高gamma 频段，时变SJC copula 互信息要高于其他copula 互信息。 随着频段由高到低，时变copula 互信息呈现逐渐上升的规律，而值较低的静态copula互信息无此迹象。 这体现出不同类型的copula 函数估计出的互信息完全不同，静态copula 互信息可能无法正确挖掘出肌间耦合强度关系。

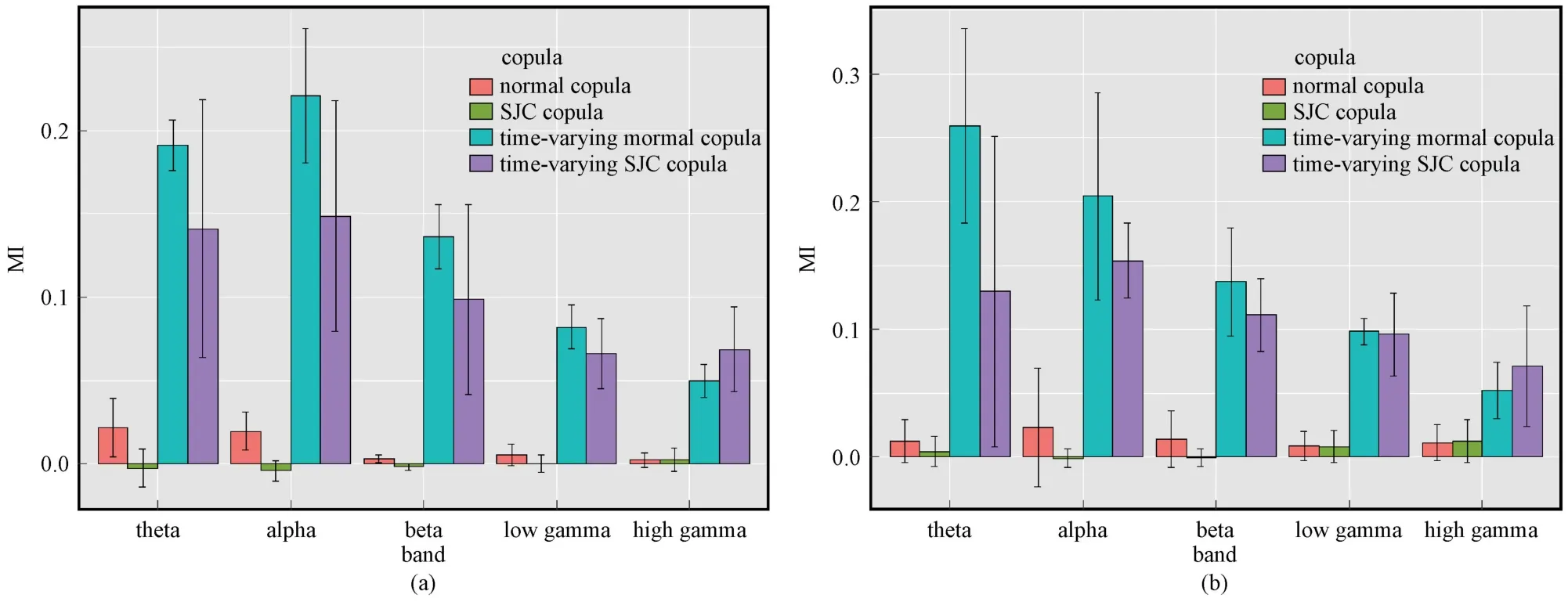
图4 静态和时变copula 互信息对比。 (a) 腕屈；(b) 腕展Fig.4 Comparison of static and time-varying copula MI.(a) WF； (b) WE

为了比较静态和时变copula 互信息的性能，表3 给出了所有受试者根据AIC 最小原则在每一次腕部动作、每一个特征频段上所选择的copula 函数类型的累计情况(总共10 名受试者×2 种腕部动作×6 次重复×5 个特征频段＝600)。 所有受试者都选择了时变copula 函数作为最佳的连接函数，其中时变normal copula 占了65.67%，时变SJC copula 占了34.33%。 这说明:时变copula 函数比静态copula函数更适合描述肌间耦合关系，由时变copula 函数得出的互信息更适合度量肌间耦合强度的大小；但是，单一的时变copula 函数难以描述复杂的肌间耦合关系。 结合图4 的对比情况可知，在一定频段范围内，相较于时变SJC copula 互信息，时变normal copula 互信息更适合度量肌间耦合强度的大小。

表3 所有受试者关于copula 函数的选择情况Tab.3 Selection results of copula functions for all subjects

2.2.2 不同频段和动作下时变copula 互信息对比

为便于后续分析，这是将最佳的时变copula 互信息用于度量肌间耦合强度。 图5(a)、(b)分别给出了所有受试者在腕屈、腕展时，BB 与TB 在5 个特征频段上时变copula 互信息的对比结果。 其中，同时标出了独立样本T检验后的P值，实心小圆点表示受试者样本。 从图5 的箱型图的分布情况来看，两种腕部动作下，不同特征频段间的时变copula互信息都表现出完全一致的规律，即:theta 频段的时变copula 互信息要显著高于alpha 频段的值(P<0.05)，alpha 频段的时变copula 互信息要显著高于beta 频段的值(P<0.000 1)，beta 频段的时变copula互信息显著高于低gamma 频段的值(P<0.000 1)，低gamma 频段的时变copula 互信息要显著高于高gamma 频段的值(P<0.01)。 这说明，腕屈和腕展运动过程中，肌间耦合强度存在明显的频段差异。

图5 不同频段上时变copula 互信息的对比(实心小圆点表 示 受试者 样 本；∗:P<0.05，∗∗:P<0.01，∗∗∗:P<0.001，∗∗∗∗:P<0.000 1)。 (a) 腕屈；(b) 腕展Fig.5 Comparison of time-varying copula MI in different frequency bands (solid dots represent the subject samples.∗: P < 0.05，∗∗: P < 0.01，∗∗∗: P <0.001，∗∗∗∗: P<0.000 1).(a) WF； (b) WE

图6 给出了所有受试者两种腕部动作过程中，BB 与TB 在5 个特征频段上的时变copula 互信息的对比结果。 可以看出，除了theta 频段外，在其他特征频段上，腕屈和腕展动作间的时变copula 互信息均不具有显著性差异(P>0.05)。 这说明，BB 与TB 在alpha、beta、低gamma 和高gamma 频段上， 肌间耦合强度基本维持稳定，不随腕部运动方式的变化而改变。 而theta 频段上的差异(P＝0.049<0.05)，能够将腕屈与腕展区别开来，说明肌间耦合强度在这一频段与运动的执行方式相关联。 更加具体地，表4 给出了所有受试者基于时变copula 互信息的肌间耦合强度大小，以供参考。

表4 肌间耦合强度(平均值±标准差，bit)Tab.4 Intermuscular coupling strength (mean ± standard deviation， bit)

图6 不同频段上腕屈和腕展的时变copula 互信息对比Fig.6 Comparison of time-varying copula MI in different bands during WF and WE movements

2.2.3 时变copula 互信息与生理指标的相关性分析

进一步，还分析了所有受试者腕屈、腕展动作过程中，BB 与TB 在5 个特征频段上平均时变copula 互信息与受试者的年龄、身高和体重之间的相关性，结果如图7 所示。 图中拟合好的平滑直线表示平均时变copula 互信息与受试者的年龄、身高和体重的相对变化趋势。 从图7 可以看出，各个特征频段上的平均时变copula 互信息与受试者的年龄、身高和体重均无明显的相关关系，在经皮尔森相关性检验后发现，P值均大于0.05，这说明腕屈、腕展运动过程中，肌间耦合强度不受个体生理定量指标的影响。

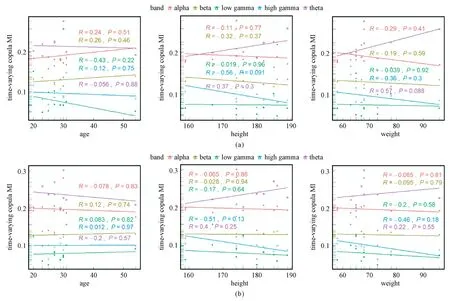
图7 时变copula 互信息与受试者年龄、身高和体重之间的相关性。 (a) 腕屈；(b) 腕展Fig.7 Correlation between time-varying copula MI and age， height， weight of subjects.(a) WF；(b) WE

3 讨论

肌间耦合是指运动过程中肌肉间的相互作用，在一定程度上反映了运动中枢神经系统对相关肌肉的控制支配作用。 肌间耦合强度体现为肌肉的激活程度和协调程度，可作为运动功能康复评估的生理指标[20]。 研究运动过程中肌间耦合特性，对于理解神经运动控制策略以及运动功能障碍机制具有十分重要的意义。

然而，现有的肌间耦合分析方法存在诸多不足，肌间耦合关系尚未被很好理解。 鉴于目前copula 函数种类众多，任何一种都很难完全刻画出肌间复杂的相关结构，所以本研究将copula 理论中别具特色的时变copula 函数引入到肌间耦合分析之中。 时变copula 函数不仅继承了静态copula 函数所具有的特点，而且还因其参数时变而更具灵活性和优越性，对相关结构的描述也更加准确。 此外，不同于由静态copula 函数导出的相关测度在时间维度上保持恒定不变，时变copula 函数能够反映相关结构的动态演化过程，更加符合实际情况。

在时变copula 函数的基础上，本研究通过与信息熵理论相结合，提出了时变copula 互信息方法，并给出了切实可行的计算步骤。 时变copula 互信息具有多元、非负、对称和对单调变换不敏感等特点。 与其他肌间耦合分析方法(如时域的相关系数或频域的相干性)相比，时变copula 互信息不对数据分布做任何先验假设，能更好地度量肌间线性或非线性耦合强度；与依赖概率密度函数定义的互信息相比，时变copula 互信息避免了对联合概率密度函数的估计，使估计的结果更精确，拓展了互信息的适用范围。 同时，传统的经验分布函数具有良好的统计性质，当样本量足够大时，能够很好地拟合总体分布，估计出的边际分布函数可以减少因平滑假设所带来的误差[21]。 典型极大似然估计可以不用估计边际分布中的参数，只需估计时变copula 函数中的时变参数，在边际分布未知或拟合效果欠佳的条件下，是一种不错的保守估计方法[22]。

腕屈和腕展是日常生活中手腕活动最常见的两种方式。 本研究基于时变copula 和时变copula互信息，深入研究了腕屈、腕展运动过程中，BB 和TB 在theta、alpha、beta、低gamma 和高gamma 共5个特征频段的耦合情况。 实验结果显示，在不同特征频段上，无论是腕屈运动还是腕伸运动，时变copula 函数的拟合优度都要明显高于静态copula 函数的拟合优度，时变copula 函数对肌间相关结构的刻画更充分(见表2)；静态copula 相关系数在不同特征频段上均接近于0，而时变copula 相关系数显示在不同特征频段上，肌间存在波动程度不同的时变相关性，随着频段的上升，时变相关系数变化越剧烈，上、下尾时变相关系数与频段分布存在一定的联系，总体上呈现为正相关(见图3)；在度量肌间耦合强度时，静态copula 互信息会造成一定的低估(<0.05 bit)，而时变copula 互信息的估计结果更加准确，多数情况下，时变normal copula 互信息更加契合肌间耦合关系(见图4 和表3)。 重要的是，本研究发现，在腕屈、腕展运动过程中，不同特征频间肌间耦合强度存在显著的统计学差异(P<0.01，见图5 和表4)，表现为:theta 频段的肌间耦合强度要显著高于alpha 频段的值，alpha 频段的肌间耦合强度要显著高于beta 频段的值，beta 频段的肌间耦合强度要显著高于低gamma 频段的值，低gamma 频段的肌间耦合强度要显著高于高gamma 频段的值，这或许表明，神经肌肉系统可能被组织成一个多重平行和分层控制结构，不同的通路支持不同频率波段的共同输入，这与Boonstra 等使用相干性分析得出肌间耦合网络在不同频段上存在广泛连通性的结论[23]基本一致。 此外，两种腕部动作相差无几，仅在theta 频段发现腕屈过程的肌间耦合强度要显著低于腕展过程(P<0.05，见图6)。 这可能与中枢神经系统的模块化控制策略有关，即腕屈和腕伸动作下都具有共享的协同模块和任务特殊的协同模块，肌肉活动可表现为sEMG 信号在不同频率范围的振荡协同作用[24]。 本研究还进一步发现，肌间耦合强度与个体生理指标之间并无明显的相关关系(见图7)，提示不同被试的频域指标不具有显著的个体差异性，这与Jaiser 等的发现[25]基本吻合。

当然，本研究仍存在一些不足之处。 从理论上讲，很难找到一种完美的copula 函数形式能够全面地描述神经生理信号之间的耦合关系，时变copula函数自身也存在一定的局限性。 最近，Chang 等提出了权重系数和相关系数均时变的时变混合copula函数[26]，综合了时变copula 和混合copula 的优点，这将是笔者下一步工作的研究重点。

4 结论

本研究将时变copula 函数引入到肌间耦合分析中，提出了一种时变copula 互信息估计方法，用于描述不同特征频段上的肌间耦合关系。 实验结果表明，在腕屈、腕展运动过程中，相比静态copula函数，时变copula 函数对肌间相依结构的似然程度更高；由时变copula 互信息导出的肌间耦合强度存在显著的频段差异，具体表现为频段越高肌间耦合强度越低，而静态copula 互信息低估了肌间耦合强度；进一步发现，肌间耦合强度与受试者的年龄、身高和体重无关。 时变copula 互信息是一种十分有效的肌间耦合分析手段，对挖掘潜在的中枢神经系统运动控制机制具有良好的应用价值。