基于被动听觉ERP范式的慢性意识障碍患者个体评估研究

王小宇 杨 艺 李 凡 陈雪玲 高寒冰 马兆楠 何江弘∗ 丛丰裕∗

1(大连理工大学电子信息与电气工程学部生物医学工程学院， 辽宁 大连 116024)

2(首都医科大学附属北京天坛医院神经外科， 北京 100700)

引言

意识障碍(disorders of consciousness， DoC)是指各种严重脑损伤导致的意识丧失状态，如昏迷、植物状态(vegetative state， VS) 和微意识状态(minimally conscious state， MCS)等。 其中，意识丧失超过28 d 的意识障碍为慢性意识障碍(prolonged DoC， pDoC)[1-3]。 目前，pDoC 的检查与评估采用修改版昏迷恢复量表(coma recovery scale-revised，CRS-R)作为标准临床量表[4-5]。 近年来，脑功能检测技术应用范式与分析方法的优化丰富了pDoC 的临床评估体系， 如脑电(electroencephalography，EEG)， 功能性磁共振成像(functional magnetic resonance imaging， fMRI)，功能性近红外光谱成像(functional near-infrared spectroscopy， fNIRS)等[6-8]。其中EEG 因其便携、可床旁开展以及可实时观测等优势而具备较强的应用潜力[9]。

使用EEG 进行pDoC 患者意识水平评估的应用范式主要包括:静息态EEG，经颅磁刺激联合脑电图(transcranial magnetic stimulation with EEG， TMSEEG)，事件相关电位(event related potentials，ERPs)等[9]。 其中ERPs 是指由感官，认知或运动等刺激素材诱发的特异性脑电反应[10]。 特别是被动听觉ERPs 范式，即仅需受试者聆听声音刺激而不要求其进行任何行为反应，适用于认知反应能力下降的pDoC 患者[11]。 该实验的声音序列通常以oddball 范式呈现，即在重复出现的标准刺激中偶尔出现与其在声音属性上有差异的偏差刺激(如标准刺激为1 000 Hz，偏差刺激为1 200 Hz)[12]。 该范式可诱发:(1)表征必要性听觉感知过程的N1 成分；(2)表征自动化偏差辨识过程的失匹配负波成分(mismatch negativity， MMN)；(3)表征注意力自动定向的P3a 成分[13]。 Kotchoubey 等[14]发现N1成分在VS 患者中出现的比例要显著低于MCS 患者。 Wijnen 等[15纵向评估了10 位由VS 恢复至MCS 状态的pDoC 患者，发现MMN 的幅值随着意识水平的恢复而显著增高。 笔者近期的研究也表明了MMN 的幅值与pDoC 患者的CRS-R 评分存在统计显著的相关性[16-17]。 Fischer 等[18]研究者率先提出使用唤名刺激诱发P3a 成分来评估pDoC 患者意识水平。 然而，上述研究证据仍局限于组别水平的统计分析结果，被动听觉ERP 范式在pDoC 患者个体水平的评估效能尚待挖掘。

近年来，研究者尝试利用机器学习算法来实现DoC 患者意识水平个体评估[19-20]。 其底层逻辑为:在被动听觉ERP 范式中，标准刺激仅可诱发必要性成分(如N1)，偏差刺激还可额外诱发表征偏差辨识过程的MMN 成分[21]。 这样，机器学习算法对两类刺激对应的EEG 信号区分准确度高，则表示MMN 成分被成功诱发；反之，则无MMN 成分。2013年，Tzovara 等[19]提出一种基于脑地形图模式分解的单试次(single-trial)分类方法来评估DoC 患者对标准与偏差刺激的区分程度。 该团队对昏迷后约48 h 的患者进行两次被动听觉ERP 评估(间隔约为24 h)；进一步，利用其提出的机器学习算法分别计算个体被试在两次评估中的解码准确率(利用脑电信号区分标准与偏差试次)。 研究发现，两次评估中解码准确率的差值可预测患者日后能否存活。 特别地，该结果指出根据个体被试数据建立特异性模型，即训练与测试的单试次样本均来自于同一位被试，取得的解码准确率与DoC 患者当前意识水平无统计相关性。 此后，Armanfard 等[20]提出可首先利用健康受试者的数据进行模型训练，这样可首先保证模型对标准/偏差刺激分类精度；进一步，利用给定DoC 患者数据进行测试；最终，以局部特征选择(localized feature selection， LFS)算法输出该DoC 患者数据与健康被试组总体ERP 反应相似度。 结果表明该算法可在健康被试数据中取得92.7%的解码准确率，且这种基于相似性度量的机器学习方法成功预测了两名DoC 患者的预后恢复[20]。 然而，该方法是以叠加平均后的波形为样本进行分类，即单被试的评估仅由两个样本决定(标准与偏差刺激样本各1 个)。 因此，该结果的统计可信度仍需提高。

为了解决上述问题，根据被动听觉范式下N1和MMN 成分的特性，提出一种pDoC 患者个体评估的深度学习算法，具体包括两个方面:一是提出一种单试次融合的数据扩增方法，有效提高个体被试的样本数量；二是结合深度学习模型，实现自动化特征提取及分类识别。 旨在利用真实pDoC 患者数据验证该方法的有效性，为基于被动听觉ERP 范式的pDoC 患者个体评估提供新的研究思路。

1 材料和方法

1.1 被试信息及EEG 采集

1.1.1 pDoC 被试

自2017年1月至2018年12月在中国人民解放军第七医学中心共计招募100 名pDoC 患者。 每位患者的意识水平由至少2 名经验丰富的临床医师基于CRS-R 量表评定。 经过评估，pDoC 被试包含58 名VS 和42 名MCS 患者。 EEG 数据采用21 导联(国际标准10－20 系统)设备记录(Nicolet， Natus Neurology)，且均在DoC 患者处于行为清醒状态时于床旁记录。 EEG 采样频率为1 000 Hz；在线参考电极为CPz；电极阻抗均低于10 kΩ，大多数低于5 kΩ。经过后续数据排查，共有6 名患者EEG 数据存在强烈噪声，故排除。 最终，有效记录的数据为54 名VS 和40 名MCS 被试(详见表1)。 所有患者家属均签署了知情同意书，得到了中国人民解放军第七医学中心伦理委员会批准。

表1 意识障碍患者信息统计表Tab.1 Information about patients with disorders of consciousness

1.1.2 健康被试

为了有效挖掘pDoC 被试中脑功能反应接近于健康被试的患者，如运动认知分离患者或闭锁综合征患者。 在样本类别中加入了健康对照被试的数据。 在大连理工大学招募了38 名健康大学生参加实验，年龄(26.2 ± 2.9)岁。 所有受试者均听力正常。 EEG 数据采用64 导联(国际标准10－20 系统)设备记录(ANT Neuro， Enschede， Netherlands)。 为了保证与pDoC 患者EEG 数据的可比较性，后续处理中只保留与患者EEG 数据相同的21 个通道数据。 采集参数为:采样频率1 000 Hz；在线参考电极为CPz；电极阻抗均低于10 kΩ，大多数低于5 kΩ。所有受试者均处于声音屏蔽室中参加本次实验。在实验过程中，被试仅需聆听声音序列，同时观看无声电影。 在向被试解释了的目的后，所有受试者均签署了知情同意书。 得到了大连理工大学伦理委员会的批准。

1.2 实验范式

以双频率偏差偶发范式来诱发被动听觉ERPs成分，具体为:1 000 Hz 纯音信号为标准刺激(standard， STD)；1 050 Hz 和1 200 Hz 纯音信号为小偏差刺激(small deviant， SD)和大偏差刺激(large deviant， LD)；所有声音刺激持续时长均为200 ms，相邻刺激间隔(stimulus onset asynchrony， SOA)为1 000 ms。本实验范式的具体参数为:整个实验共包括1 000 个声音刺激且以伪随机形式呈现；STD，SD和LD 的出现概率分别为0.8，0.1，0.1，且相邻两个偏差刺激之间至少存在3 个STD。 声音序列的编程控制使用E-Prime 3.0 软件(Psychology Software Tools， Pittsburgh， PA)。 实验总时长约为17 min。实验范式详见文献[17]。

1.3 EEG 处理与分析

1.3.1 预处理

EEG 信号的预处理及分段过程均使用Matlab(Version 2019a)环境和EEGLAB 工具箱完成[22]。首先，人工剔除原始数据中的明显伪迹，如被试身体移动等原因造成的EEG 剧烈波动；随后，利用球形样条差值方法来替换数据中噪声极强的通道[23]。滤波过程采用EEGLAB 中的自带滤波函数以50 Hz陷波滤波，1 Hz 高通滤波和30 Hz 低通滤波的顺序进行。 滤波后的数据重参考至双侧乳突电极(M1和M2) 的均值。 最后，采用独立成分分析(independent component analysis， ICA)去除眼动和眨眼等伪迹；ICLabel 工具箱用于伪迹成分的自动化识别[24-25]。

1.3.2 分段

预处理后的数据需进一步进行分段处理，具体为:以刺激起始点为0 时刻，拆分成长度为500 ms的单试次数据，包括刺激前100 ms 数据作为基线以及刺激后的400 ms 数据。 随后，所有单试次数据进行基线校正，且校正后幅值绝对值仍超过75 μV 的单试次数据将被剔除。 为了更好地提取MMN 成分，所有偏差试次将点对点减去其对应的前一个标准试次，即计算差异波。 最终，个体被试将包含三类单试次数据:标准试次STD，大偏差刺激对应的差异波数据(即大偏差试次减去其前一个标准试次的波形，LD)和小偏差刺激对应的差异波数据(即小偏差试次减去其前一个标准试次的波形，SD)。

1.3.3 ERP 量化

在被动听觉ERPs 实验中，主要关注STD 试次中的N1 成分，以及LD 和SD 试次中的MMN 成分。根据文献[16]，MMN 成分的潜伏期与DoC 患者的意识状态无显著相关性。 因此，将首先分析N1 和MMN 成分的幅值在3 组被试中的统计差异。 N1/MMN 成分幅值的测量过程为:以Fz 为观测电极，根据组别叠加平均的波形确定N1/MMN 成分的波峰；以该波峰对应的潜伏期为中点，取－20～20 ms 时间窗内波形的平均幅值作为N1/MMN 成分的幅值。

1.4 深度学习框架

1.4.1 单试次样本随机融合扩增

理想状况下，个体被试数据共包含800 个STD，100 个LD 和100 个SD 单试次样本，分别记为xSTD，xLD，和xSD，且均为19(电极数)×125(采样点数)的矩阵。 提出将个体被试数据中的三类单试次样本进行空间级联以形成时空特征融合的单试次样本(后文统一称为融合样本)，该过程为

式中，xfusion为融合样本，其大小为57(电极数)×125(采样点数)。

图1 为单试次样本随机融合扩增流程图。 假设该融合样本可有效整合标准试次中N1 成分和偏差试次中MMN 成分的信息。 进一步，该融合样本可从个体被试三类数据中分别随机抽取单试次样本进行空间级联而成，这样个体被试的单试次样本数量便由100(偏差试次数量上限)提高至约106(3 种类型试次的组合数)。

图1 单试次融合样本扩增流程。 (a)3 类单试次样本，标准样本为标准试次波形，大/小偏差样本为大/小偏差刺激对应的差异波波形(即偏差试次减去其前一个标准试次的波形)；(b)单试次样本随机融合；(c)单试次融合样本Fig.1 Flowchart of single-trial sample augmentation.(a) Single-trial samples of three types of stimuli， in which standard samples are the single trials corresponding to standard stimuli， and large/small samples are the singletrial difference waveforms corresponding to large/small stimuli (difference waveform was calculated by subtracting the deviant sweep from the standard sweep preceding that deviant stimulus)； (b) Random fusion of samples； (c) Fusing samples

1.4.2 EEGNET 算法

进一步采用EEGNET 深度学习算法对输入的单试次样本实现自动化特征提取和分类识别，其为Lawhern 等研究者于2018年提出的一种面向EEG数据分析的基于卷积神经网络的深度学习框架[26]。目前，该算法已在多个脑机接口范式中(如P300 和运动想象等范式)取得了高精度且高鲁棒性的分类表现。 该算法由两个模块组成。 其中，第一个模块执行两个步骤:(a)一个作为频率滤波器的时序卷积层计算时序特征；(b)一个作为空间滤波器的深度卷积层学习特定频率的空间特征。 第二个模块为由深度卷积和逐点卷积组成的深度可分离卷积层，来单独学习每个特征图的时序特征并优化特征组合。 每个模块后均对特征进行全局平均池化处理。 采用的EEGNET 参数与其原始论文中保持一致[26]。

1.4.3 交叉验证

旨在提高被动听觉ERP 范式下pDoC 患者个体识别精度，故所用数据集按被试组别划分为VS，MCS 和健康对照组(healthy control， HC)三类，即个体被试样本的标签。 共纳入132 名被试(38 名HC、40 名MCS 和54 名VS 患者)，在被试层面采用11折交叉验证，每折包含12 名被试的单试次数据；其中，前9 折数据包括每类4 名被试，第10 折数据由2名HC，4 名MCS 以及6 名VS 患者构成，第11 折数据由12 名VS 患者构成。 该交叉验证方式可确保训练集和测试集样本不来自于同一名被试，即确保训练集与测试集间样本的陌生性。 在测试阶段，个体被试所有单试次样本的总体测试结果将表示该被试在样本水平(sample level)的分类准确率；进一步，个体被试样本中被预测频次最高的类别将代表该被试的预测类别，即个体被试的评估结果由所有单试次样本共同决定。 因此，11 折交叉验证后会得出每个被试在样本水平的分类准确率，以及所有被试在被试水平(subject level)的分类准确率。 为了确保方法的稳定性，完整的11 折交叉验证共重复10 次。 上述两个准确率，以及被试水平的精确率(Precision)和召回率(Recall)将作为评估模型表现的指标。 这些指标表示为

式中，TP，TN，FP，FN 分别为真阳性(true positive)，真阴性(true negative)，假阳性(false positive)和假阴性(false negative)的样本数量。

在当前的三分类(HC，MCS 和VS)任务下，被试水平的精确率和召回率取为各类的平均值。

1.4.4 EEGNET 特征的可解释性

采用基于梯度计算的显著图(saliency map)来确定在单试次水平各特征(如单个电极下的单个采样点)对分类结果的贡献度[27]。 其中，各类别被正确预测样本的显著图将被叠加平均来表示该类别的总体显著图。 显著图的量纲被归一化至0～1。 在此量纲下，幅值越接近1 表示该特征对分类结果贡献度越大，幅值越接近0 表示该特征对分类结果贡献度越小。 为了量化三组被试显著图模式的相似性，采用二维相关系数(Matlab 中corr2( )函数)计算每两类样本显著图的相关系数。 进一步，选取5个典型电极区域，即前额区，颞区，中央区，顶区，枕区来量化不同脑区对分类结果的贡献度。 此时，每类样本的显著图(融合样本的显著图本是由STD，LD 和SD 等3 类样本空间级联而成)被拆分成STD，LD 和LD 各自的贡献度。 最终，计算各脑区在各自样本类型下的贡献度比例。

1.4.5 统计分析

采用单边t检验统计N1/MMN 成分的幅值与0是否存在显著差异，即确认各被试群体是否被有效诱发出N1/MMN 成分。 单因素重复测量方差分析被用于统计N1/MMN 成分幅值在3 组被试之间的差异性。 对于深度学习模型的评估，以样本水平和被试水平的分类准确率以及被试水平的精确率和召回率为观测值，利用单因素重复测量方差分析来研究:(1)融合样本与非融合样本对分类准确率的影响；(2)融合样本的扩增数量对分类准确率的影响，进而确定合适的样本扩增数量。 利用显著图中的贡献度比例作为观测值，采用单因素重复测量方差分析来研究不同脑区对总体分类结果的影响，进而理解EEGNET 在本分类任务下学习到的任务相关特征。 统计分析中显著性水平为0.05；若观测值不满足Mauchly 球形检验，则利用Greenhouse-Geisser 方法校正自由度和P值；Bonferroni 方法用于多重比较校正。 所有统计分析内容均在SPSS(IBM SPSS Statistics， Version 22)软件上进行。

2 结果

2.1 ERP 波形和脑地形图

图2 为Fz 电极处组平均波形图及相应脑地形图结果，其中STD(见图2(a))为标准试次波形，LD和SD(见图2(b)和(c))为大/小偏差刺激对应的差异波波形。 单边t检验结果显示:在STD 条件下，3 组被试的N1 成分幅值显著小于0(VS:P＝0.016<0.05； MCS:P<0.001； HC:P<0.001)；在LD 条件下，MCS 和HC 组的MMN 成分幅值显著小于0(MCS:P＝0.046<0.05； HC:P<0.001)，VS 组的MMN 成分幅值与0 无统计显著差异(VS:P＝0.208>0.05)；在SD 条件下，仅HC 组的MMN 成分幅值显著小于0(HC:P<0.001)，MCS 与VS 组的MMN 成分幅值与0 均无统计显著差异(MCS:P＝0.496>0.05； VS:P＝0.793>0.05)。

图2 Fz 电极处组平均波形图及相应脑地形图。 (a)标准刺激(标准试次波形)；(b)1 200 Hz偏差刺激(偏差试次减去其前一个标准试次)；(c)1 050 Hz偏差刺激(偏差试次减去其前一个标准试次)Fig.2 Group-averaged waveforms at Fz electrode and the relevant topographies.(a) Standard stimuli； (b)1 200 Hz deviant stimuli (Subtracting the deviant sweep from the standard sweep preceding that deviant stimulus)； (c) 1 050 Hz deviant stimuli (Subtracting the deviant sweep from the standard sweep preceding that deviant stimulus)

对于3 组被试之间N1/MMN 幅值的统计分析，单因素重复测量方差分析结果显示:在STD 条件下，N1 成分幅值组别主效应显著(F＝17.033，P<0.001)。 多重比较分析结果显示:N1 成分幅值的绝对值符合VS0.322，P<0.001； 1.605>0.258，P<0.001)，MCS 和VS 组MMN 幅值绝对值无统计显著差异(幅值绝对值:0.322>0.258，P>0.05)。 在SD 条件下，MMN 成分幅值组别主效应显著(F＝17.254，P<0.001)。 多重比较分析结果显示:HC 组MMN 绝对值幅值显著高于MCS 和VS 组(幅值绝对值:0.918> 0.122，P<0.001； 0.918>0.267，P<0.001)，MCS 和VS 组MMN 幅值绝对值无统计显著差异(幅值绝对值:0.122<0.267，P>0.05)。

2.2 单试次样本类型影响分类表现的对比结果

为了验证空间级联三类单试次样本的时空特征融合策略在DoC 个体评估中的有效性，本节研究对比了单试次融合样本与非融合样本对分类表现的影响。 为了确保结果的可比性，所有个体被试的单试次样本数量均取为100，即偏差刺激对应单试次样本数量的上限。 图3 为以各类型单试次样本为输入时模型的分类表现。 在样本水平，单因素重复测量方差分析结果显示:样本类型主效应显著(F＝108.068，P<0.001)。 多重比较分析结果显示:融合样本的分类准确率要显著高于单独使用其中任何一种类型样本(均满足P<0.01)；仅使用STD 单试次作为输入样本取得的分类表现也显著高于单独使用任意一种偏差试次样本(均满足P<0.01)；单独使用两种偏差单试次作为输入样本时，模型分类表现无显著差异(P＝0.603>0.05)。

图3 不同类型样本下的模型分类表现Fig.3 Classification performance in different types of samples

表2 为以各类型样本为输入时，模型重复运算10 次的平均分类表现。 在被试水平，模型分类表现与样本水平结果趋势保持一致。 单因素重复测量方差分析结果显示:准确率，精确率和召回率的样本类型主效应均显著(F＝45.456，P<0.001；F＝30.824，P<0.001；F＝37.192，P<0.001)。 多重比较分析结果显示:融合样本的分类准确率，精确率和召回率都要显著高于单独使用其中任何一种类型样本(均满足P<0.05)；仅使用STD 单试次作为输入样本取得的分类表现也显著高于单独使用任意一种偏差试次样本(均满足P<0.01)；单独使用两种偏差单试次作为输入样本时，准确率，精确率和召回率无显著差异(均为P>0.05)。

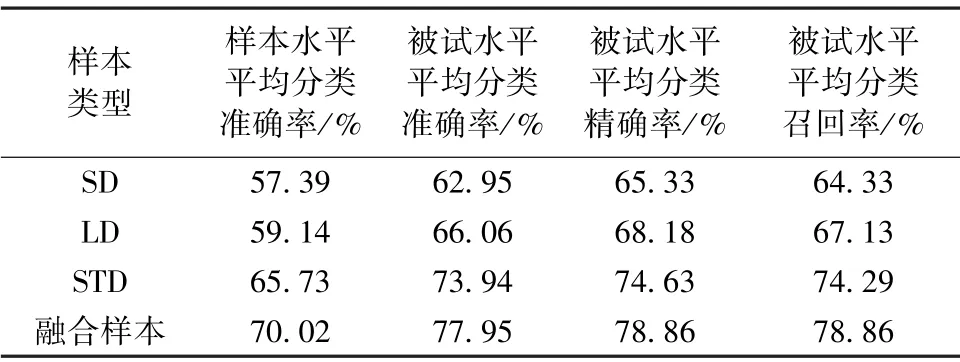
表2 不同类型样本下的模型分类表现Tab.2 Classification performance in different types of samples

2.3 融合样本的扩增数量影响分类表现的对比结果

如方法部分描述，所提出的单试次融合样本可由个体被试数据中3 类单试次的随机组合而成。 因此，该方法可有效扩增个体被试的单试次样本数量。 本节研究对比了融合样本的扩增数量对模型分类表现的影响，进而确定当前分类任务下合适的样本扩增数量。 图4 为单被试融合样本数量由100增加至1 000 时模型的分类表现。 在样本水平，单因素重复测量方差分析结果显示:样本数量主效应显著(F＝101.575，P<0.001)。 多重比较分析结果显示:样本数量从100 扩增到200 时，模型分类表现显著提高(分类准确率:70.02% <73.03%，P＝0.001<0.01)；当样本数量由200 扩增到300 时，模型分类表现无显著变化(分类准确率:73.03%<73.79%，P>0.05)；当样本数量由200 继续扩增到400 时，模型分类表现又出现显著提高(分类准确率:73.79%< 74.44%，P＝0.004<0.01)；随后，样本数量由400 扩增至1 000 时，模型分类表现无显著提升，但平均分类准确率仍由74.44%提升至最高75.14%。

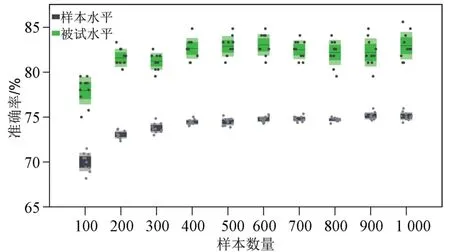
图4 不同融合样本数量下的模型分类表现Fig.4 Classification performance in different number of fusing samples.

表3 为单被试融合样本数量由100 扩增至1 000时，模型重复运算10 次的平均分类表现。 在被试水平，单因素重复测量方差分析结果显示:准确率，精确率和召回率的样本数量主效应均显著(F＝13.682，P<0.001；F＝12.460，P<0.001；F＝10.375，P<0.001)。 多重比较分析结果显示:当样本数量大于等于200 时，分类准确率显著提升，即样本量为200 至1 000 时，被试水平分类准确率均显著高于样本数量为100 时的分类准确率；当样本数量由200 扩增至1 000 时，模型分类表现无显著提升，但平均分类准确率仍由81.59%提升至最高83.00%。 同时，精确率和召回率的统计结果趋势同准确率结果一致，均在样本数量扩增至1 000 时，取得分别为83.79%和84.02%的最佳分类表现。

表3 不同融合样本数量下的模型分类表现Tab.3 Classification performance in different number of fusing samples.

2.4 EEGNET 特征

本节研究以基于梯度计算的显著图来揭示当前分类任务下EEGNET 模型学习到的分类特征模式。 图5 为被正确预测的三类样本的总体显著图。从图中可看出，MCS 与HC 组显著图有较高相似性，而VS 组与MCS/HC 均表现出较低相似性。 二维相关分析结果为:r(MCS，HC)＝0.970，r(VS，HC)＝0.560，r(VS，MCS)＝0.470。

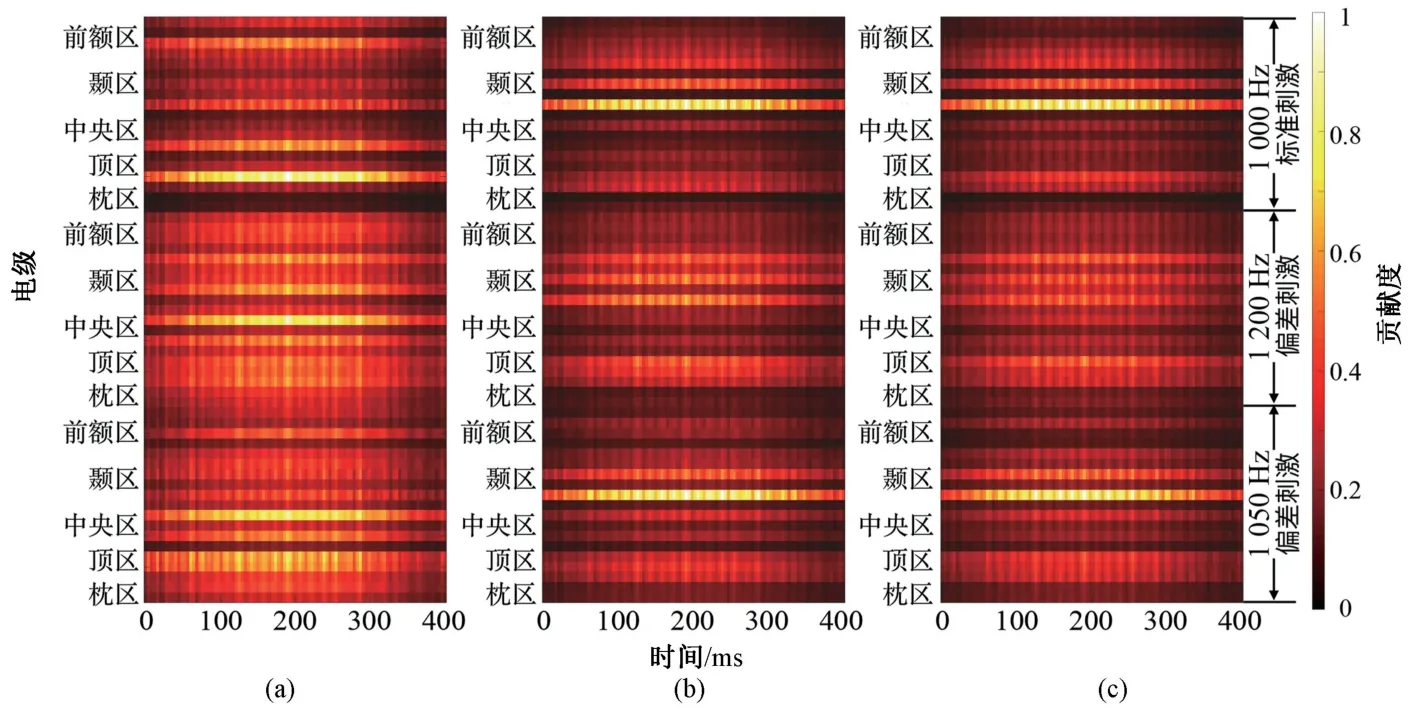
图5 不同组别样本下的特征显著图。 (a)植物状态组；(b)微意识状态组；(c)健康对照组Fig.5 Saliency maps in different groups.(a) Vegetative state group； (b) Minimally conscious state group； (c)Healthy controls.

进一步，量化了在3 组被试中5 个脑区对分类的贡献度。 图6 为3 组被试中3 种刺激条件下各脑区贡献度比例的直方图。 单因素重复测量方差分析结果显示:脑区间主效应显著(F＝23.589，P<0.001)。 多重比较分析结果显示:枕区和中央区电极对分类结果贡献度要显著小于前额区，颞区和顶区(均满足P<0.05)；前额区，颞区和顶区对分类结果贡献度无显著差异。 表4 为3 组被试中3 种刺激条件下各脑区贡献度比例。

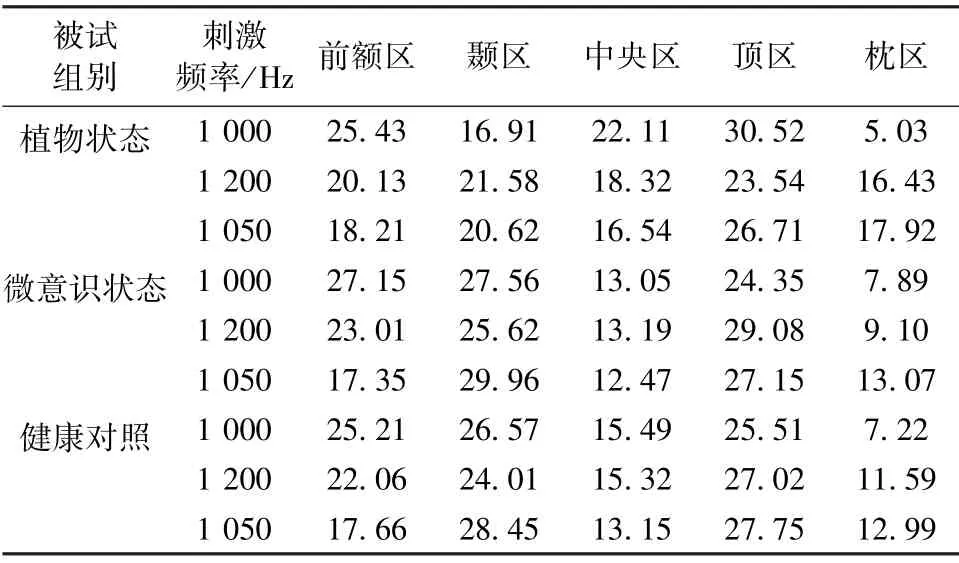
表4 不同组别样本下5 个典型脑区的特征贡献比例(%)Tab.4 Attributions ratio (%)of five typical brain regions in different groups

图6 不同组别样本下五个典型脑区的特征贡献比例直方图(a)植物状态组；(b)微意识状态组；(c)健康对照组Fig.6 Histogram of attributions ratio of five typical brain regions in different groups.(a) Vegetative state group； (b) Minimally conscious state group； (c)Healthy controls.

3 讨论

3.1 时空特征融合策略提升模型分类表现

基于特征工程的机器学习方法常在单个样本中融合多种类特征，如Armanfard 等[20]在单样本中融合了统计特征(如方差，偏度和峰度等)，频率特征(如alpha， beta 频段能量)和时频特征(小波分解系数等)等信息来解码大脑加工标准与偏差刺激的差别。 从特征融合的角度出发，提出将个体被试数据中3 类单试次时域波形(STD，LD 和SD)在空间级联以形成时空特征融合的单试次样本。 为探索该融合样本对模型分类表现的影响，分析了分别以STD，LD，SD 和融合样本为输入样本时，模型的分类表现。

研究表明融合样本(在样本数量为100 时)可在样本水平和被试水平分别取得70.02% 和77.95%的平均分类准确率，以及被试水平78.86%的精确率和召回率，均显著高于非融合样本的分类表现。 正如之前的研究报道，标准试次中包含的强制性听觉N1 成分以及偏差试次(经过差异波计算)中包含的表征自动化偏差辨识的MMN 成分均为pDoC 诊断的关键脑功能指标[13]。 但因为上述两个ERP 成分表征不同阶段的听觉信息加工过程，以往研究通常将其视为两个独立的观测指标来分析其对DoC 评估的有效性。 结果表明将同一范式下的多个ERP 成分联合分析可实现pDoC 患者个体评估精度的提升。 类似地，Pan 等[28]利用同一脑机接口范式下的P300 成分和连续EEG 信号中的视觉稳态诱发电位( steady-state visual evoked potential，SSVEP)联合评估pDoC 患者意识水平。

因此，在利用EEG 进行pDoC 评估时，特征融合的方式不仅可以是融合表征同一大脑加工过程的多个特征(如融合时域和频域特征联合表征MMN成分[20])，也可以是融合同一实验范式下的多个大脑加工过程(如本研究融合同一被动听觉范式下的N1 和MMN 成分)。 上述特征融合方式均可有效地丰富单个样本的特征维度，进而提高DoC 个体评估精度。

3.2 随机融合扩增策略提升模型分类表现

如前文所述，时空特征融合单试次样本是由个体被试数据中3 类单试次时域波形随机空间级联而成。 对此，我们推测在随机形成的融合样本数量较少时，模型可能无法习得个体被试数据的整体分布；而且，样本数量的增加可有效提升EEGNET 等深度学习算法的分类表现[29]。 为探究融合样本的扩增数量对模型分类表现的影响，对比了融合样本数量由100 扩增至1 000 时模型的分类表现。 结果表明随着融合样本扩增数量的增加，模型的分类表现会随着样本数量的扩增而提升并逐步趋于平稳。样本水平分类准确率在样本数量扩增至400 时，模型分类表现趋于平稳；而被试水平的分类表现在样本数量扩增至200 时便未能继续显著提升。 从总体趋势来看，样本水平和被试水平的最佳分类表现均在样本数量扩增至1 000 时取得，分别为75.14%和83.00%。 由此可见，融合样本的扩增数量是影响模型分类表现的关键因素之一。

实际上，在图像识别领域，研究者通常采用图像几何变换和添加噪声等方式进行数据扩增[30]。然而，以单试次时域波形作为样本而非图像，且床旁采集的pDoC 患者脑电数据具有强烈噪声干扰，故上述两种数据扩增方式均不合适。 根据当前分类任务的实际应用场景，本研究采用了随机融合策略来对不同刺激类型的单试次时域波形进行空间级联。 该随机过程起到了样本扩增的作用，并结合深度学习模型的强大特征学习能力实现了模型分类表现的提升。 此外，是面向被动听觉ERP 范式提出的深度学习算法，因此该方法可能同样适用于其他利用被动听觉ERP 范式进行离线个体评估的应用场景(如精神分裂症[31]和阅读障碍[32])。

3.3 融合样本特征贡献模式分析

以EEGNET 深度学习模型来实现样本自动化特征提取和分类识别。 进一步，采用了基于梯度计算的显著图(saliency map)在单试次水平确定各特征对分类结果的贡献度，即EEGNET 模型从融合样本中学习到的特征模式。 而且，每两组被试间显著图的二维相关结果显示MCS 组与HC 组具有较高相似度(r(MCS，HC)＝0.970)，但上述两组均与VS 组相似性较低(r(VS，HC)＝0.560，r(VS，MCS)＝0.470)。 该结果可能表明:尽管MCS 患者意识水平下降，其在被动听觉ERP 范式下的大脑反应模式仍与HC 存在较高相似度，所以EEGNET 可在MCS 患者和HC 被试中采用相同的特征提取策略来完成识别任务；对于VS 患者，其在本实验范式下的大脑反应活动与HC 和MCS 被试存在明显差异，故EEGNET 模型能够提取出与上述两组不同的特征模式来实现分类任务。

上述推测也能在3 组被试的N1/MMN 幅值得到部分验证:N1 成分在3 组被试中均被成功诱发；在LD 条件下，MMN 成分仅在MCS 和HC 组出现，却未能在VS 出现。 总体来看，显著图结果表明与HC 组大脑反应模式的相似性是MCS 和VS 患者之间的一个重要差异。 该结果也一定程度证明了Armanfard 等[20]提出的度量被动听觉ERP 范式下DoC 患者与健康对照组EEG 响应模式的相似性来评估其意识水平的合理性。

进一步，以往研究表明N1 成分和MMN 成分在头表激活的典型区域为前额区和中央区。 笔者之前的研究也表明在Fz 和Cz 电极下测得的MMN 幅值可与DoC 患者临床CRS-R 评分存在显著相关性[16-17]。 故进一步计算了各脑区在当前分类任务下的贡献值。 结果表明枕区和中央区电极对pDoC患者个体评估的贡献最低且显著低于前额区，颞区和顶区电极，而上述3 个脑区之间对分类任务贡献无显著差异。 由此可见，EEGNET 模型学习到的特征模式并非仅利用N1/MMN 成分的典型激活区域，同时也利用了顶区电极来丰富特征维度。 因而推测EEGNET 利用了ERP 成分的整体空间分布以完成当前分类任务。

相较于传统分析方法仅在典型电极下(如Fz，Cz)观测MMN 等成分的幅值以进行意识水平评估，近来发展的机器学习评估模型常依赖于更多电极数据，如32 导[20]甚至256 导EEG 设备[33]。 此外，Engemann 等[34]发现电极数量的减少会降低基于EEG 手段的DoC 患者分类精度；特别地，当电极数量低于16 时，DoC 评估准确率会显著降低。 因此，在利用机器学习算法进行DoC 评估时，EEG 设备的电极数量是影响评估准确性的重要因素，并且应该考虑利用不低于16 导的EEG 设备来保证识别精度。

3.4 局限性

本研究尚存在一些不足:(1)采用的数据集存在(a)患者组与对照组年龄不匹配以及(b)两组被试的脑电数据采集自不同设备的问题。 Cheng等[35]报道了相较于年轻人(年龄在20～40 岁)，老年人(年龄在50～80 岁)由被动听觉范式诱发的MMN 幅值显著降低。 采集设备对被动听觉范式下ERP 成分的影响尚无明确研究。 上述问题均可能造成数据整体偏移，进而影响判别模型的可靠性。尽管已采用三分类任务(HC，MCS 和VS 等3 个组别，其中MCS 和VS 组年龄匹配且采集设备一致)来规避该风险，但鉴于目前数据所限，尚无法对该问题造成的风险进行有效估计。 (2)采用的数据集均为个体被试的单次采集结果，致使目前无法测试本深度学习框架对于同一患者在意识恢复过程中的评估敏感性。 (3)采用的数据集均来自于同一个医学中心，尚无法测试本深度学习框架对于多医学中心数据的泛化能力。 希望随着日后数据量的丰富，以上局限性可被有效解决。

4 结论

本研究提出一种适用于被动听觉ERP 范式下pDoC 患者个体评估的深度学习算法。 根据该范式诱发的N1/MMN 成分的特性，本算法提出样本融合的数据扩增策略并结合EEGNET 深度学习算法实现pDoC 患者个体评估。 该机器学习算法可有效克服被试特异性模型评估能力差的问题，实现样本水平和被试水平平均分类准确率分别为75.14%和83.00%以及被试水平83.79%精确率和84.02%召回率的最佳评估表现，为pDoC 患者个体评估提供了新的研究思路。