处理含参集合运算问题的常用策略

蔡宝祥

(江苏省盐城市东台市三仓中学)

集合的基本运算(包括交集、并集、补集)是历年高考的必考内容,常用的求解方法有列举法、借助数轴、Venn图加以分析等.求解含有参数的集合问题,需要灵活采取合理、有效的方法,求解过程中往往会因思维不严密导致错误.本文侧重谈谈如何具体求解含有参数的集合运算问题,以切实帮助学生拓宽解题思维,提升解题能力.

1 借助“检验分析”

处理“利用列举法表示含参集合,且给定集合运算结果”这类集合问题时,解题的关键步骤可归纳为以下两点:一是求值检验——由给定的集合运算结果,往往可直接求得参数的值,但需要注意根据集合中元素的互异性和集合运算结果加以检验分析(否则,极易出错)；二是活用规律——分析、解决目标问题时,要注意有关规律在解题中的灵活运用(例如:若集合M中含有n(n∈N*)个元素,则其子集共有2n个,真子集共有2n－1个).

例1 设集合A＝{a,0},B＝{－4,log2(a＋3)2},若A∩B＝{0},则集合A∪B的真子集的个数为( ).

A.5 B.6 C.7 D.8

因为A∩B＝{0},所以0∈B,则有log2(a＋3)2＝0,即(a＋3)2＝1,解得a＝－2或－4.

检验分析:当a＝－2时,集合A＝{－2,0},B＝{－4,0},此时A∩B＝{0},满足题意；当a＝－4时,集合A＝{－4,0},B＝{－4,0},此时A∩B＝{－4,0},显然不满足题意.

于是,a＝－2,集合A＝{－2,0},B＝{－4,0},所以A∪B＝{－4,－2,0},该集合一共有3个元素,其真子集的个数为23－1＝7,故选C.

一般地,求解此类含参集合问题需要关注以下两点:一是考查集合中元素是否满足“互异性”；二是考查含参集合是否有可能为空集(因为空集具有特殊性质).

2 借助“分类与整合思想”

一般地,处理含参集合运算问题,往往需要讨论；而具体讨论时,要做到“不重不漏”.特别地,含参集合可能在参数取某个值时为空集,而空集参与集合运算时具有特殊性质.

例2 已知集合A＝{x|x2＋x－6＝0},B＝{x|mx＋1＝0},是否存在实数m,使得A∩B＝B?若存在,求出m的值；若不存在,说明理由.

3 借助数轴上的“动静结合”

处理“利用描述法表示集合,其中约束条件以不等式形式给出,且给定集合运算结果或集合关系”这类集合问题时,解题的关键步骤可归纳为以下两点:一是让含参集合表示的范围,在数轴上由左向右运动变化进行动态分析；二是根据给定集合运算结果或集合关系,准确构建不等式或不等式组,进而求解参数

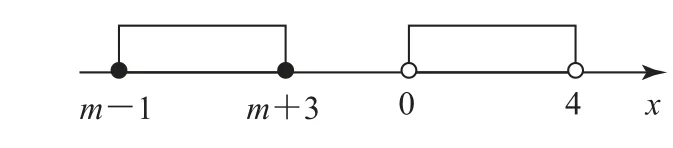
图1

图2

(2)在数轴上先表示集合B,再让集合C表示的范围在数轴上由左向右运动变化,结合图3 分析即知,由B∪C＝R,得

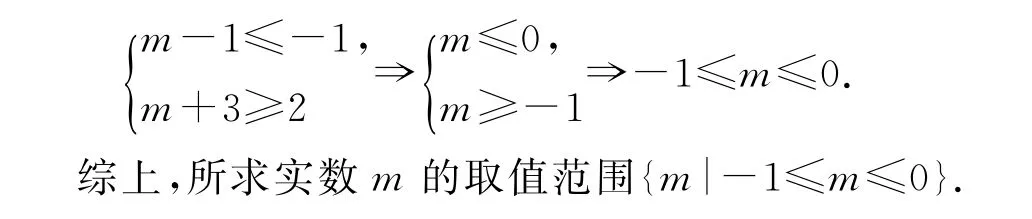
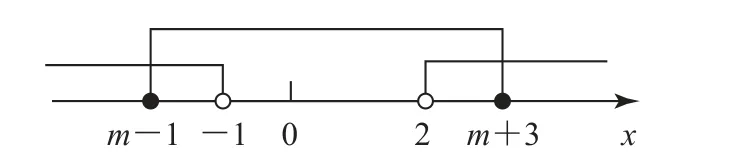
图3

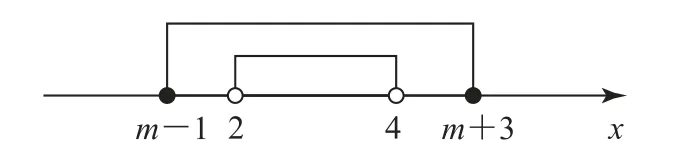
图4

对于“由给定的集合运算结果或集合关系,求参数的取值范围”这类问题,一般情况下应以数轴为载体,采取“动静结合”的方法,有利于迅速厘清含参集合与确定集合之间的位置关系,进而建立不等关系加以求解.此外,还需要注意结合题意,准确分析不等关系中的“等号”能否取到；否则,极易出错.

综上,关注含参集合运算问题的常用解题策略,有利于灵活运用所学知识、方法解决问题.