基于特征模型的挠性航天器接触消旋控制
李 超, 何英姿, 胡 勇1,
1. 北京控制工程研究所,北京 100094 2. 空间智能控制技术重点实验室,北京 100094
0 引 言
截至2021年,大约有4500颗卫星在轨运行,在广播通信、天气预报、资源测绘、水资源监测等军事和民用领域发挥巨大的作用[1].有很多卫星在运行期间出现故障[2].对于高价值的失效卫星,空间机器人在轨维修是延长卫星寿命的一种有效方法[3-4].
消旋是指施加外部力矩衰减空间目标角速度的过程.根据目标与消旋机构的接触状态,消旋方式分为接触式和非接触式.两类方式各有特点.接触式执行机构简单易于实现,消旋力矩更大;非接触式安全性更高,碰撞风险更小.
在接触式消旋中,有一种由空间机械臂操纵柔性消旋刷触碰目标的方案,吸引了大量国内外学者的关注.段文杰等[5]设计基于消旋刷线弹性接触力模型的前馈控制器,有效抑制接触力对空间机械臂基座姿态的扰动.吴昊等[6]设计基于计算力矩法的滑模控制,有效克服了由消旋刷引入的机械臂末端参数不确定性.LIU等[7]采用Jourdain速度变分原理建立消旋系统模型,模拟了消旋刷和目标的运动.WANG等[8]设计章动目标接触消旋最优控制律.CHENG等[9]设计一种根据目标角速度幅值调整接触点的消旋策略.
目前已有的接触消旋研究成果通常不考虑航天器挠性附件的影响.然而,对于含有大型太阳帆板的失效卫星,挠性附件的影响不可忽略.比如消旋刷施加的接触力矩作为持续激励的干扰源,会激发目标的挠性振动[10],增加对象模型不确定性,加大控制器设计难度.因此,有必要研究考虑挠性振动抑制的接触消旋控制方法.
针对航天器挠性结构的振动抑制控制,现今主要有主动控制和被动控制两种方法[11].主动控制方法的思路是首先在帆板上安装智能材料作为执行机构,然后设计抑制帆板振动的控制算法.常见算法有速度反馈控制[12]、独立模态控制[13]、正位移反馈控制[14]等.被动控制的主要思想是尽量减小中心本体控制系统对挠性振动的激发,主要有设计结构滤波器、添加阻尼装置等方法.
还有一类基于航天器本体执行器的集中式姿态控制方法.这类方法的思路是将挠性结构的振动视为干扰或模型不确定性,采用滑模变结构控制[15]、自适应控制[16]、模糊控制[17]、最优控制[18]等方法,通过本体的执行器抑制挠性振动.
本文将特性模型理论[19-20]应用到失效卫星接触消旋控制问题中,提出一种基于特征模型的挠性振动抑制方法,并通过数值仿真验证所提方法的有效性.
1 接触消旋系统模型
1.1 模型描述
图1描述了典型的接触消旋场景.上方为翻滚的失效卫星,它由卫星本体和一对挠性太阳帆板组成.Oxyz是目标本体坐标系,O为目标质心,ωx、ωy、ωz为目标绕本体坐标系的角速度,x轴是目标的旋转轴,H是目标角动量,φ为目标章动角.服务卫星处于目标旋转轴的正下方,它包含空间机械臂和一只柔性消旋刷.
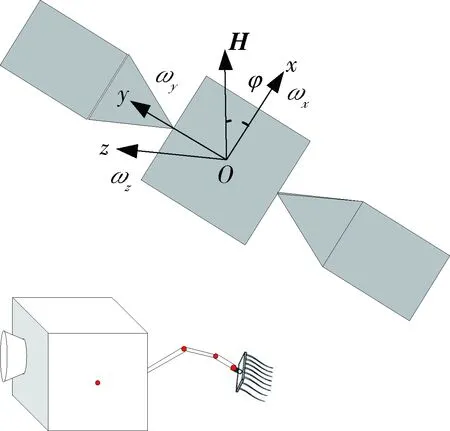
图1 接触消旋场景Fig.1 Contact detumbling scene
图2是接触消旋过程的典型情况示意图.左侧为服务卫星,右侧为失效卫星,目标绕质心O旋转.图2(a)为接触前示意图,服务卫星借助携带的敏感器估计目标位姿信息,通过消旋控制算法计算得到消旋刷位置;图2(b)为接触时示意图,服务卫星通过机械臂操控消旋刷到预定位置,触碰目标本体上平行于x轴的棱边S1S2,消旋刷发生弹性形变,吸收目标动能,转化为自身弹性势能,衰减目标角速度;图2(c)为接触后示意图,消旋刷与目标帆板脱离,服务卫星调整姿态,回到图2(a)的状态,等待与目标的下一次接触.将图2(a)与图2(c)称为非接触段、图2(b)称为接触段.
1.2 失效卫星运动模型
自由旋转失效卫星的姿态动力学方程为
(1)
式中:I为目标的转动惯量矩阵;ω=[ωx,ωy,ωz]T为目标的角速度;η=[ηl,ηr]T为帆板的挠性振动模态坐标,ηl、ηr分别对应左右帆板挠性模态;Br=[Brl,Brr]为转动耦合系数矩阵,Brl、Brr分别对应左右帆板耦合系数矩阵.
挠性振动模态坐标的动力学方程为
(2)
式中:ξ为帆板的模态阻尼系数;ωf=diag{ωl,ωr}为帆板的模态频率矩阵;ωl、ωr分别对应左右帆板模态频率.

图2 接触消旋过程示意图Fig.2 Schematic diagram of contact process
1.3 控制力矩模型
接触消旋的执行机构是一个消旋刷,结构如图3所示.消旋刷由刚性连杆、固定底座和多根柔性毛刷构成.刚性连杆被固定在空间机械臂的末端,用以保证机械臂与目标间的安全距离.
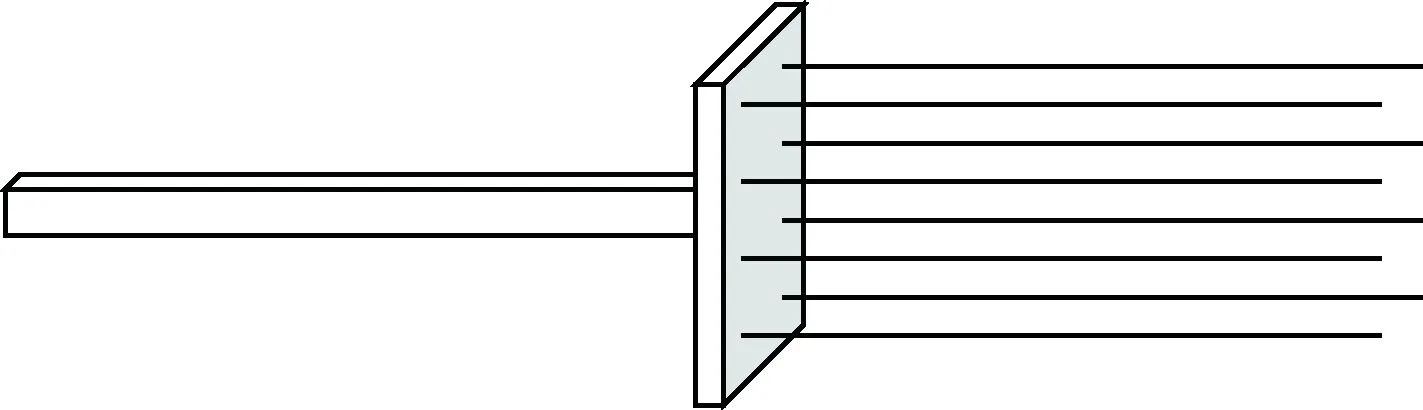
图3 消旋刷结构图Fig.3 Structure diagram of detumbling brush
图4是发生接触碰撞时的示意图.S1S2是目标本体上平行于x轴的一侧棱边,E是目标质心,P是S1S2的中点.将多根柔性毛刷的影响等效为单根消旋刷,用GF表示.
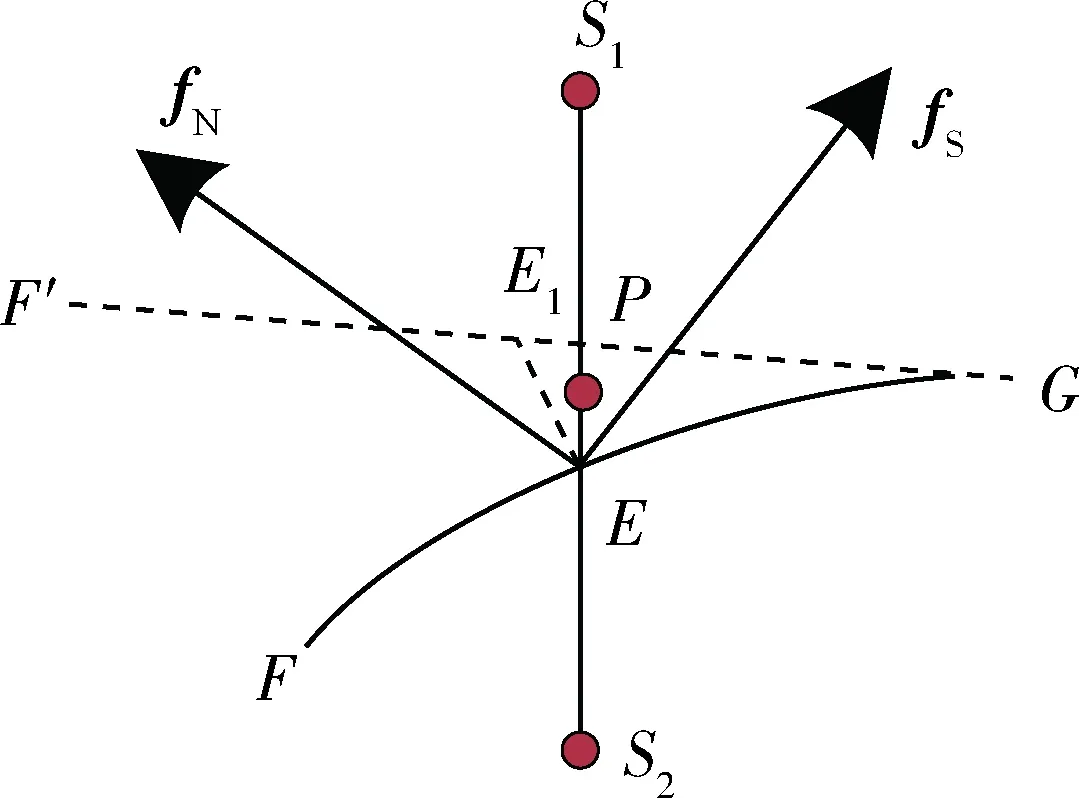
图4 接触碰撞示意图Fig.4 Contact collision diagram
消旋时GF触碰S1S2,随着目标转动,消旋刷发生形变,接触初始时刻消旋刷所在直线为GF′.
E1E是S1S2与GF′的公垂线.设rG、rF′、rS1、rS2、rE1、rE为G、F′、S1、S2、E1、E的位置坐标,则rE1、rE可以通过求解方程得到[8].
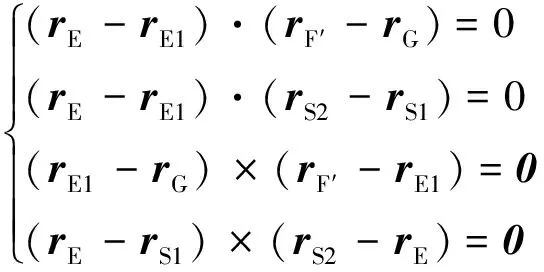
(3)
在初始接触时刻,E1与E重合,GF′与S1S2相交于E.由于GF与S1S2接触的时间非常短,接触点在S1S2上的位置变化很小,因此将E近似作为接触点,并近似认为GF、GF′共面.
应用线弹性接触力模型,可得接触时目标受到的正压力fN和摩擦力fS的大小分别为
(4)
fS=μS·fN
(5)
其中uE为E相对GF′的距离,EI为材料的抗弯刚度,lGE为GE的长度.
图4中,fN⊥fS,fN与EE1的夹角为
(6)
fN的三维空间表达式为
(7)
其中n1为描述fN方向的向量,表达式为
(8)
同理,fS的三维空间表达式由式(9)、(10)计算得出.
(9)
(10)
设O到E的位置向量为rOE,则接触力矩为
T=rOE×(fN+fS)
(11)
接触消旋系统含有两个控制量:接触初始时刻消旋刷深入量u1和接触点的偏移量u2.在图4中,u1=|E1F′|,u2=sign(u2)·|PE|,
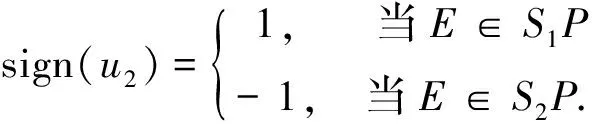
采用文献[21]的分离式接触消旋策略,用u1衰减x轴角速度ωx,用u2衰减y轴角速度ωy,而z轴的角速度ωz依靠三轴角速度之间的耦合关系衰减.
综上,当消旋刷与目标发生接触时,消旋对象的表达式为
(12)
2 基于特征模型的消旋控制
在挠性航天器接触消旋时,目标最大惯量轴存在明显挠性振动.本节首先建立描述最大惯量轴挠性振动角速度的特征模型,然后基于特征模型设计挠性振动抑制控制律,最后给出挠性航天器消旋的控制律u1和u2.
2.1 挠性振动系统的特征建模
设目标的最大惯量轴为x轴,建立x轴的挠性振动特征模型.仅考虑单一通道,忽略其他通道的耦合,接触时角速度的动力学方程可以写为
(13)
其中:Brx、Tx分别为x通道的转动耦合系数和消旋力矩;Ix为x通道的惯性矩.
设存在与目标惯量、尺寸、初值完全相同的刚性失效卫星,将其在相同接触力矩下的运动称为参考运动.将参考运动的x轴角速度记为ω0,在接触时ω0满足
(14)
设存在时变比例系数λ(t),使得
(15)
则式(13)可以写为
(16)
设消旋系统采样周期为Δt,对目标在采样时刻的角速度ωx[(k+1)Δt]泰勒展开,得
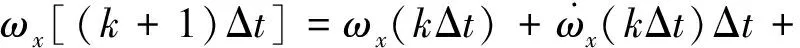
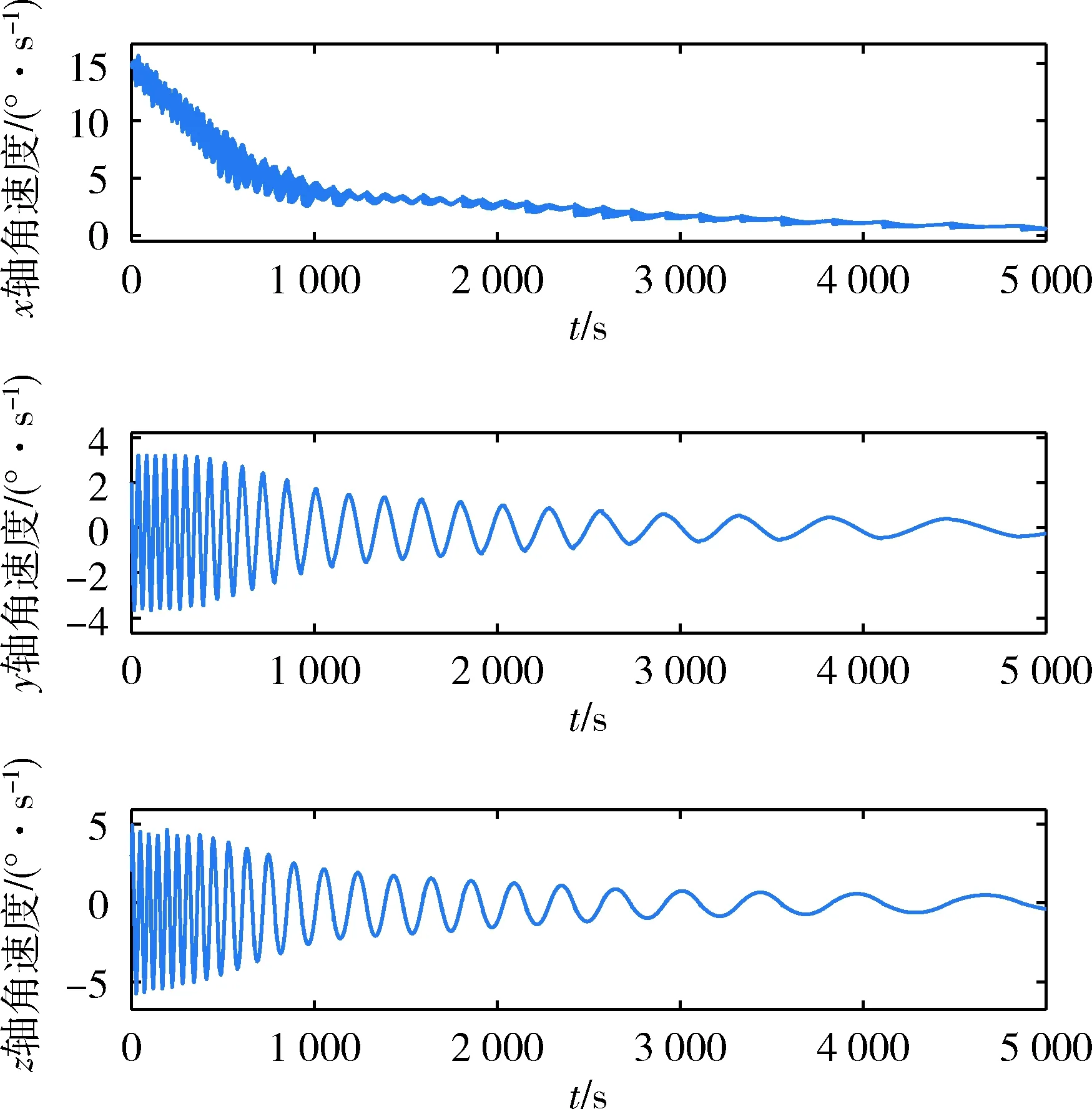
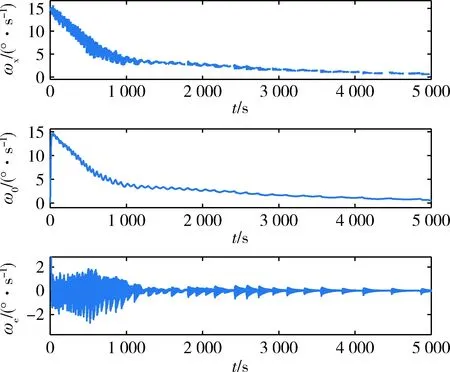
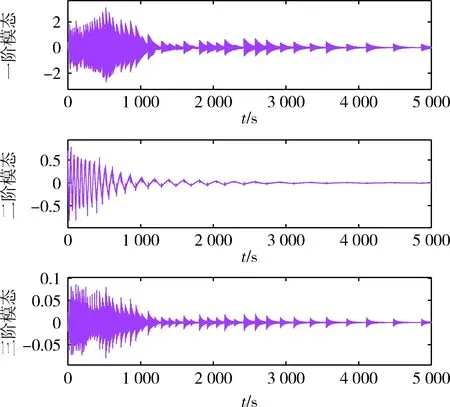
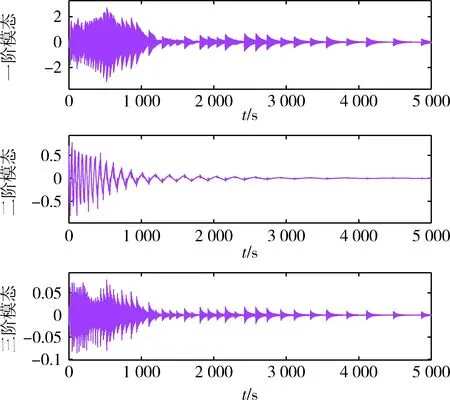
式中,0 (17) (18) 其中λ(k)=λ(kΔt).同理,对参考运动在采样时刻的角速度ω0[(k+1)Δt]做相同处理,得 (19) 其中0 (20) 其中ωe=ωx-ω0为角速度偏差量,它由挠性附件的振动耦合引起.称ωe为挠性振动角速度. 设θ为接触段目标绕x轴的转角,使用微分中值定理,写出Tx在点(u0,θ0)=(0,0)处的一阶泰勒展开式为 Tx=bu1+F (21) (22) 其中 (23) 定义压缩函数,将Δ压缩到特征参数中,令 (24) 其中N>0,是一个小的常数.将式(24)代入式(22)得 (25) 最终的特征模型表达式为 ωe(k+1)=f1(k)ωe(k)+g0(k)u1(k) (26) 特征参数f1(k)、g0(k)分别为 (27) (28) 建模误差为 由图2可知,接触消旋存在“间歇性”控制特点.接触段的接触力矩T≠0,非接触段的接触力矩T=0.因此特征模型式(26)也符合该特性,非接触段u1(k)=0. (29) 图5 接触时刻时间轴示意图Fig.5 Timeline diagram of contact detumbling 首先,将ωx拆分为ωx=ω0+ωe.ω0和ωe的定义与2.1节相同.对u1的控制要求是尽快衰减ω0,同时保证ωe尽量小. 针对ω0,采用PD控制律 u10(k)=Kp1ω0(k)+Kd1[ω0(k)-ω0(k-1)] (30) 其中Kp1、Kd1是u10的比例和微分系数. 针对ωe,基于特征模型式设计挠性振动抑制反馈控制律 (31) (32) u10与u1f有不同的控制需求.一方面,u10要保证ω0尽快衰减到零,需要接触力矩越大越好;另一方面,u1f要保证ωe尽量小,需要接触力矩衰减ωe时避免激发挠性振动.为同时满足这两种需求,整合u10与u1f,令 u′1=(1-γ)u10+γu1f (33) 其中γ为常数,满足0<γ<1.通过调节γ平衡控制需求:增大γ,衰减ωe的比重更大;减小γ,抑制ω0的比重更大. (34) 其中0≤i≤n-1,ωepre(k)=ωe(k),n为预测的第m次接触持续的时间步长,由前(m-1)次接触时间估计得出.设ωeb为根据消旋任务指标预设的误差带(ωeb>0),当|ωepre(k+n)|>ωeb时,施加预测控制律 (35) 式中,l2为小的正常数. 最后,根据上述PD控制、挠性振动抑制反馈控制、预测控制设计u1的控制律为 u1=(1-γ)u10+γu1f+u1fpre (36) 针对y轴角速度ωy,设计控制律u2为 u2(k)=sgn(ωy(k))·{Kp2|ωy(k)|+ (37) 其中Kp2、Kd2是u2的比例和微分系数. 为验证本文提出控制方法的有效性,对非合作失效卫星接触消旋进行仿真.选取目标前3阶挠性模态,各阶模态频率及目标尺寸如表1所示. 表1 目标参数Tab.1 Target parameters 目标的转动惯量参数为 (38) 太阳帆板的转动耦合系数矩阵为 (39) (40) 采用的消旋刷参数如表2所示.初始时刻目标的角速度为[15,2,3]T(°)/s. 表2 消旋刷参数Tab.2 Brush parameters 仿真中目标三轴角速度曲线如图6所示.当t<1 000 s时,目标转速较高,为了保证消旋过程的快速性,不采用挠性振动抑制,u1采用的控制律为u1(k)=u10(k),u10由式(30)给出,u2采用的控制律为式(37).当t>1 000 s时,目标转速较低,为了保证消旋过程的平稳性,提高控制精度,采用挠性振动抑制控制律,u1的控制律变为式(36),u2不变.该图表明,消旋刷的接触力矩在衰减目标角速度的同时,成为扰动源,激发了目标的挠性振动,且目标最大惯量轴角速度ωx的挠性振动问题最突出. 图6 三轴角速度曲线Fig.6 Angular velocity component curve 图7为x轴及相关角速度曲线图7(a).为实际角速度ωx;图7(b)为ωx经实时滤波后的角速度,对应2.1节的ω0;图7(c)为角速度偏差量ωe,ωe=ωx-ω0.ωe反映了挠性振动幅度的大小.当t<1 000 s时,ωe幅值较大;当t>1 000 s时,|ωe|<1(°)/s,表明ωe被有效抑制. 图8-9分别是左右帆板的挠性模态曲线.该图表明,当t>1 000 s时,目标的挠性振动被有效抑制,说明了本文方法的有效性. 图10是控制量曲线.(a)(b)分别是控制量u1和u2的曲线,其中图10(a)为u1的各分量变化曲线,“-u1fpre”表示u1fpre反号后的曲线.控制器在消旋刷与目标即将发生接触前根据当前目标角速度更新控制量,当消旋刷与目标接触时以及与目标分离后,控制量不发生改变. 图11为接触力矩曲线.当消旋刷与目标接触时,接触力矩作用于目标上实现消旋;随着目标的旋转,消旋刷与目标分离,接触力矩为零,体现“间歇性”控制特点. 图7 x轴及相关角速度曲线Fig.7 ωx and associated angular velocity curve 图8 左侧帆板挠性模态Fig.8 Flexible mode displacement of left solar array 图9 右侧帆板挠性模态Fig.9 Flexible mode displacement of right solar array 图10 控制量曲线Fig.10 Control variable curve 图11 接触力矩曲线Fig.11 Contact torque curve 针对含有挠性振动的非合作失效卫星接触消旋控制问题,提出一种基于特征模型的自适应控制方法.通过描述目标挠性振动角速度的特征模型,并基于该模型设计了自适应挠性振动抑制控制器,有效衰减了接触力矩激发的挠性振动.仿真结果表明通过采用本文的控制方法,目标的角速度被有效衰减且激发的挠性振动小.
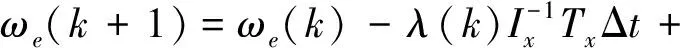
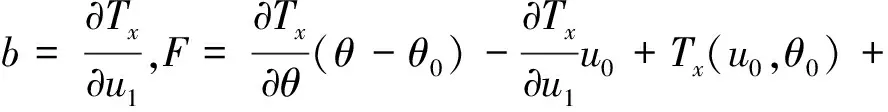


2.2 控制器设计
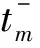


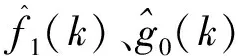
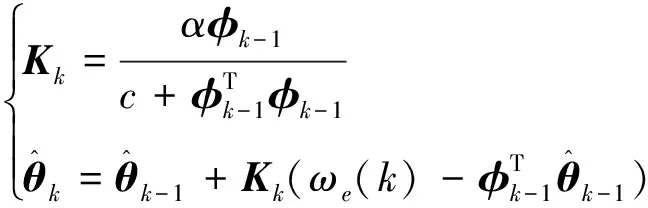
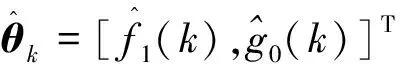

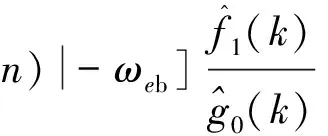
Kd2[|ωy(k)|-|ωy(k-1)|]}3 数值仿真




4 结 论

