引入DDC迁移学习算法的卫星ACS系统故障定位技术

王 泽， 程月华*， 宫江雷， 郭小红， 何漫丽

1. 南京航空航天大学 自动化学院, 江苏 南京 211100 2. 西安电子科技大学, 西安 710071 3. 宇航动力学国家重点实验室, 西安 710043

0 引 言

随着我国航天向着深空、载人、空间站等多方向的不断发展，卫星故障诊断逐渐成为一项重要的航天领域技术，是维护卫星正常在轨运行和延长在轨寿命的有力保证.常用的故障诊断方法可分为：基于模型[1]、基于信号[2]和基于数据的方法[3].其中，基于数据的故障诊断方法是目前最为热门的方向[4-6].

相较于传统的基于模型和信号的故障诊断方法，基于数据的方法具有明显的优点：其依靠大数据支持，无需构建精确的数学模型，故更加适用于实际情况.但其依赖大量的已标记数据作为训练集，这与实际卫星故障样本数据稀少的现状相冲突.

迁移学习起源于图像处理领域，是一种应对缺乏大量数据集问题的有效方法.其核心思想是将模型在丰富的源域数据集中训练，再将模型迁移到目标域中.不少国内外学者围绕上述思想，在故障诊断领域展开关于迁移学习应用的研究工作[7-8].文献[9]通过添加多层域自适应正则化项和伪标签学习正则化项，用以诊断轴承故障.文献[10]提出了一种基于TCA迁移学习的故障诊断方法，利用历史工况建立工作状态下的故障诊断模型.文献[11]提出了一种基于实例加权的多目标迁移学习网络，并以工业机器人为对象验证其故障诊断算法的准确性和鲁棒性.

文献[12]将深度迁移学习应用到卫星故障诊断问题，通过搭建基于残差的故障诊断深度学习框架，并设计网络联合分布自适应代价函数，对模型进行参数重调，使网络适用于目标任务.本文针对故障样本缺失问题，从另一种角度出发，提出一种基于DDC迁移学习算法的故障诊断方法：采用LSTM-AE模型对卫星姿态数据进行重构，得到结果并计算残差；采用统计学方法对残差提取有效特征；采用浅层网络充当故障定位分类器，并引入DDC迁移学习算法对分类器进行改进.相较于深度迁移学习，本文采用的方法具有更好的可解释性.

1 方案设计

本文提出一种基于DDC迁移学习的数据驱动故障诊断方法如图1所示.

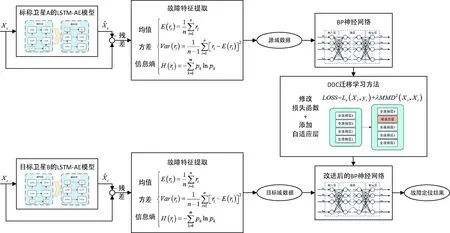
图1 基于DDC的故障定位方法结构图Fig.1 Structure diagram of fault location method based on DDC

(1)建立卫星数值仿真模型生成标称卫星A的姿态信息，采集三轴气浮台的实际数据作为目标卫星B的姿态信息，分别将标称卫星A和目标卫星B的3维姿态角和3维角速度数据通过LSTM-AE模型进行重构建模.

(2)计算残差并提取残差的均值E(r)、方差Var(r)、信息熵H(r)作为特征信息，得到标称卫星A特征集(源域)和目标卫星B特征集(目标域).

(3)使用标称卫星特征集训练BP网络，得到BP网络故障分类器.

(4)引入DDC迁移学习算法，在故障分类器网络中添加一层域适应层并修改损失函数形式，冻结浅层网络参数，利用目标卫星特征集对BP网络进行再训练，得到最终可用于实际情况的BP网络故障定位分类器.

2 方法原理

2.1 基于LSTM-AE的卫星ACS系统建模

LSTM-AE是一种由LSTM神经元构成的AE网络，其结合LSTM对长时序信息的特征学习能力和AE的无监督特性，可以高效地完成对长时序多维数据的重构.本文利用其模型对长时序多维数据的无监督重构能力，对卫星的动力学和运动学模型进行建模.

(1)

分别对标称卫星A和目标卫星B的姿态数据进行重构，对输入和输出取残差，得到标称卫星A的残差集Rs和目标卫星B的残差集Rt.

2.2 故障特征提取

为进一步对故障的特征信息进行提取，在获得残差数据后，提取残差的均值E(r)、方差Var(r)、信息熵H(r)作为特征.其中均值E(r)体现时序信息的整体偏差，方差Var(r)和信息熵H(r)体现时序信息的波动程度和无序程度，因此经过特征提取后的数据能使故障定位网络学习到更多的故障特征信息.

记ri为残差向量的第i维分量，其特征提取公式如式(2)

(2)

对残差集Rs和Rt特征提取，得到标称卫星A特征集Xs={Es，Vars，Hs}和目标卫星B特征集Xt={Et，Vart，Ht}

2.3 引入DDC迁移学习算法的故障定位

DDC[13]迁移学习方法是起源于计算机视觉领域的一种经典的深度迁移学习方法，如今也被用于解决多分类的迁移学习问题[14-17].

本文引入DDC迁移学习改善分类器网络性能：首先固定故障定位分类器网络的特征层权值，然后在特征层和输出层之间添加域适应层，使网络学习域适应知识.在训练过程中，域适应层和输出层的损失函数如式(3)

LOSS=Lc(Xs,ys)+λMMD2(Xs,Xt)

(3)

式中，Xs为源域样本，Xt为目标域样本，ys为源域标签，LOSS为总损失，Lc(Xs,ys)为源域的样本和标签产生的损失，λ为域适应损失系数，MMD2(Xs,Xt)为使用MMD函数计算得到的源域样本和目标域样本产生的损失.MMD具体计算公式如式(4)

(4)

MMD(maximum mean discrepancy)又称最大均值差异，用来衡量源域与目标域分布通过φ(·)映射到再生希尔伯特空间的距离.在迁移学习中常将MMD项加入损失函数中，让神经网络同时学习分类损失和域适应损失，以缩小源域和目标域之间的距离.φ(·)本身为未知映射，为求解上述等式，引入核矩阵K以及系数矩阵L.

(5)

(6)

其中n1为源域样本数，n2为目标域样本数.

将式(4)转换为如下形式：

MMD(Xs,Xt)=trace(KL)-λtrace(K)

(7)

进一步降维构造W矩阵使得

(8)

将上述问题转化为最优问题如下：

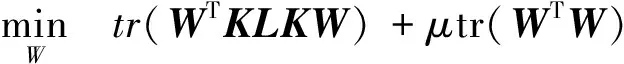
(9)

其中

H=1n1+n2-1/(n1+n2)11T
s.t.1=[1,1,…,1]n2+n2

(10)

因此，求解出(KLK+μI)-1KHK的前m个特征值，即是MMD(Xs,Xt)的值.

依据文献[13]，进行DDC迁移工作的主要任务分为3个方面：以MMD损失值为中间指标，以故障定位准确率为最终指标，通过网格搜索法结合经验选取的方式，确定最优的域适应层位置、域适应层尺寸和域适应损失系数，如图3所示.

(11)

本文引入迁移学习作为一种解决训练样本缺失的方法，这也拥有相应的局限性.当源域样本的边缘分布和条件分布与目标域样本的差距过大时，网络的域适应层将难以从源域学习到可适用于目标域的知识，从而导致在迁移学习后网络在目标域的效果依旧不佳.

3 仿真试验及分析

3.1 半物理仿真平台

本文使用半物理仿真平台采集目标卫星实际数据作为目标域数据，对算法在半物理仿真平台上进行实物验证.

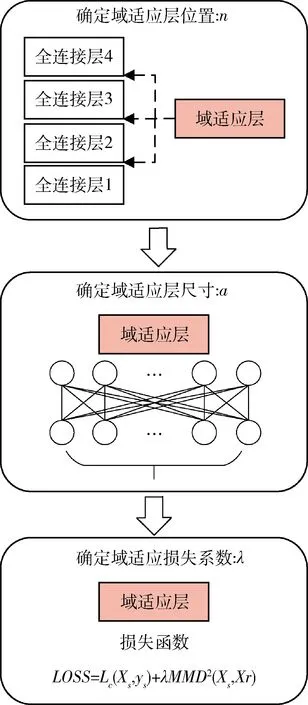
图3 DDC迁移学习步骤Fig.3 DDC transfer learning steps

图4 半物理仿真平台Fig.4 Semi physical simulation platform

如图4所示，半物理仿真平台主体分为3个部分：气浮台、姿态视觉测量系统及控制计算机.气浮台主体通过气浮轴承悬浮在底部支架上，用于模拟卫星姿态运动，其上方平面安装一个三轴陀螺仪，以测量气浮台主体角速度信息；控制计算机作为上位机接收数据，并向气浮台发送姿态指令和注入故障；姿态视觉测量系统通过上方相机捕捉气浮台主体特征靶标，并利用位姿解算方法得到气浮台姿态量，结合倾角计所测得的倾角数据计算气浮台主体的姿态角信息，具体配置如图5.

图5 姿态视觉测量系统Fig.5 Attitude vision measurement system

3.2 仿真结果

对标称卫星A(Matlab数值仿真模型)和目标卫星B(半物理仿真平台)的姿态数据进行重构，得到残差并提取特征，得到标称卫星A特征集(源域)和目标卫星B特征集(目标域).

如图6和图7所示分别为仿真数据和实际数据在健康(黑色圆点)、陀螺故障(红色星形点)、星敏故障(黄色方点)和动量轮故障(蓝色加号点)4种情况下的残差，经过故障特征提取步骤后的3维特征分布图.每张子图对应一种姿态信息残差特征，坐标轴三轴分别为均值E(r)、方差Var(r)和信息熵H(r).综合以上特征分布图可以看出，本文采用的特征提取方法效果较好，4种健康与故障情况特征点都具有明显的分布差异.

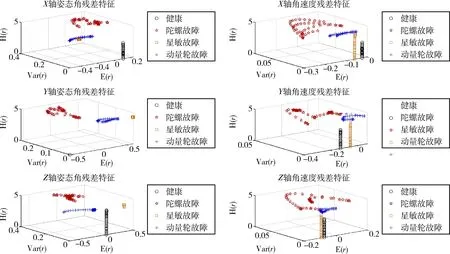
图6 健康和故障仿真数据残差特征分布图Fig.6 Characteristic distribution of residuals of health and fault simulation data

图7 健康和故障实际数据残差特征分布图Fig.7 Characteristic distribution of residuals of health and fault actual data

使用标称卫星A特征集数据对BP网络预训练，再引入DDC迁移学习算法，在BP网络中添加域适应层并利用目标卫星B特征集对BP网络进行再训练，得到最终可用于目标卫星B实际情况的BP网络故障定位分类器.

DDC迁移工作的主要任务主要分为3个方面：确定域适应层位置、确定域适应层尺寸和确定域适应损失系数.基于上述步骤内容进行实验，对网络参数修改并对比训练结果.

图8 DDC迁移学习参数选择Fig.8 DDC transfer learning parameter selection

如图8，依据DDC迁移学习步骤，首先进行域适应层位置n的确定.本文使用3层的BP网络结构，所以域适应层的添加位置只有4处.可以看出当n由1加深到3的过程中，故障定位准确率不断升高，且在第3层时准确率达到最高80.2%.因此本文选择第3层为域适应层最佳位置.

确定域适应层最佳位置n之后，进行域适应层尺寸a的确定，即该层网络的神经元数.根据文献[13]，测试使用的域适应层尺寸a之间应保持2的幂次倍数关系，可以看出在a由5增加到20的过程中，故障定位准确率持续升高，在a为20时准确率达到最高80.2%.因此本文选择域适应层最佳尺寸a为20个神经元.

经过以上两步确定工作，进行域适应损失系数λ的确定.为避免将λ设置的过低而导致网络无法学习到域之间的特征，同时也为避免将λ设置的过高而导致对原网络的过度修改和域之间的过度靠近，选择λ=0.25.

表1 DDC迁移学习效果Tab.1 Results of DDC transfer learning

在BP神经网络的DDC迁移学习训练完成之后，测试其对实际数据的故障定位准确率如上表1所示，从其统计结果可以看出，在使用DDC方法对BP网络迁移学习之后，健康情况和动量轮故障情况的定位准确率提升效果最为明显，分别为37.1%和22.3%；星敏故障的定位准确率提升最少，为10.0%.这说明本文提出的算法提高了实际情况下目标卫星ACS系统的故障定位精度.

4 结 论

本文设计了一种基于数据的故障定位方案，利用LSTM-AE对标称卫星A和目标卫星B的姿态信息重构，计算原数据和重构数据的残差提取特征信息，建立特征数据集训练BP网络分类器以定位卫星ACS故障.针对目标卫星无故障样本问题，提出了引入DDC迁移学习算法的故障定位改进方法，在原BP网络中添加域适应层并修改损失函数，以改善算法在目标卫星实际情况的定位效果.最终通过气浮台半物理仿真实验，以标称卫星A为源域，目标卫星B为目标域开展实验验证.从实验结果看，故障定位精度有了最高37.1%的提升.

由于DDC迁移学习算法只学习源域和目标域之间的边缘分布差异，而未考虑到条件分布差异.因此在源域和目标域之间条件分布差异较大的情况下，如何选取效果更好的迁移学习算法，是下一步的研究方向.