考虑状态约束的绳系组合体欠驱动控制
郭新程, 孟中杰*, 鲁迎波
1. 西北工业大学航天学院, 西安 710072 2. 郑州轻工业大学电气信息工程学院, 郑州 450001
0 引 言
随着航天技术的发展,在轨服务的重要性与日俱增.针对其关键难题:非合作失稳目标抓捕,由绳系抓捕器、系绳组成的空间绳系机器人具有诸多优势[1],引起了国内外的广泛关注.而在绳系机器人抓捕目标后,如何进行失稳目标卫星的位姿接管控制一直是关注的重点.
在这方面,文献[2-5]建立了包含百米级短系绳空间绳系系统的动力学模型,为抓捕后绳系组合体稳定控制奠定了基础.文献[6]针对大质量目标的消旋稳定问题,提出了一种解耦的PD消旋稳定控制策略;文献[7]研究了利用系绳常张力实现旋转目标星拖曳控制问题,通过设计一种常值切换控制律,利用两个恒定大小的张力实现目标的稳定控制.文献[8]考虑了翻滚目标移除中的碰撞问题,设计了一种T-S模糊控制律.文献[9]考虑了能量消耗和碰撞风险,设计了一种混合张力控制律来实现绳系系统的稳定;但是上述文献中,由于仅利用了系绳张力,目标绕绳方向的角速度不能消除.针对绳系组合体的三轴姿态稳定问题,文献[10-11]考虑了输入饱和影响,通过反步法设计了一种自适应姿态控制器,文献[12]考虑组合体稳定控制任务中输入受限及状态约束问题,设计了一种基于动态面的神经网络自适应控制方法;文献[5]提出了一种基于预设性能的自适应动态面控制方法,以保证组合体系统存在状态测量误差情况下的收敛时间、稳态误差等控制性能指标.但在上述研究中,均假设绳系系统为全驱系统.而系绳的物理特性导致直接在其面内/面外通道施加主动控制力难度极大.在考虑绳系组合体欠驱动特性的稳定控制方面,文献[13]利用偏置系绳摆杆,考虑执行器饱和,设计了一种分层滑模控制器实现欠驱动稳定控制,在此基础上,文献[14]研究了一种利用线性滑杆来实现拖曳过程中组合体的欠驱动稳定问题.文献[15]提出了一种基于能量法的空间绳系组合体欠驱动稳定控制器.在目前考虑绳系组合体欠驱动特性的控制系统设计方面,均忽略了各被控状态的强约束问题.例如,为避免系绳缠绕,目标星姿态角、系绳摆角等状态是严格受限的.
针对状态严格约束的绳系组合体欠驱动控制问题,本文在能量法的控制框架下,引入状态约束辅助函数,设计了一种欠驱动稳定控制方法,并从理论上证明了在控制器作用下,系统各状态均满足约束条件,解决绳系组合体状态约束下的欠驱动控制问题.
1 绳系组合体系统动力学模型
绳系机器人抓捕目标后的绳系组合体如图1所示,包括平台(含系绳收放装置)、系绳、目标星(含抓捕器)3部分.设o0x0y0z0为轨道坐标系,坐标原点位于组合体系统质心,o0x0轴由地心指向系统质心,o0z0轴垂直于轨道面,与轨道角速度方向一致,o0y0轴服从右手定则.o2x2y2z2为捕获后目标星(含抓捕器)本体坐标系,原点位于目标星(含抓捕器)质心,坐标轴o2x2、o2y2、o2z2为惯量主轴.otxtytzt为系绳坐标系,OXYZ为惯性坐标系.

图1 抓捕后组合体系统组成示意图Fig.1 Schematic of the postcapture tethered system
为简化建模过程,假设如下:
1)假设目标星为刚体,且空间平台具有优秀的姿/轨控制能力;
2)假设绳系组合体运行在圆轨道上,轨道角速度为ω0;
3)系绳处于张紧状态,且质量较小,忽略弹性影响,长度为l。
设状态量为q=[φ2θ2ψ2αβl]T,利用拉格朗日动力学建模方法,建立绳系组合体系统动力学模型,整理成如下二阶标准形式[5]:
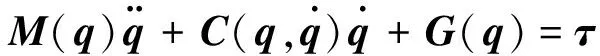
(1)
式中,τ=[τφ2τθ2τψ20 0τl]T为控制输入,

(2)
Mij,Cij,Gi(i,j=1,2,…,6)具体表达式见团队前期研究文献[5].
为了便于控制器设计,将式中状态量调整顺序.
定义qa=[φ2θ2ψ2l]T,qu=[αβ]T,u=[τφ2-G1τθ2-G2τψ2-G3τl-G6]T,则模型转换为
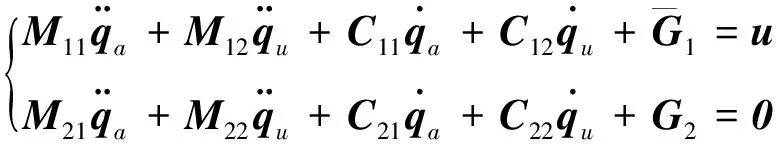
(3)
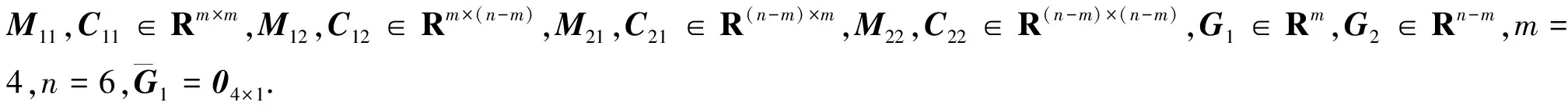
2 绳系组合体欠驱动控制器设计
2.1 控制目标
定义系统期望状态为
qd=[φ2dθ2dψ2dαdβdld]T
其中,φ2d=π/2,θ2d=0,ψ2d=0,αd=βd=0,ld为常数.
同时为了防止组合体稳定控制过程中系绳缠绕,保证系统的安全性,系统状态应满足如下约束:
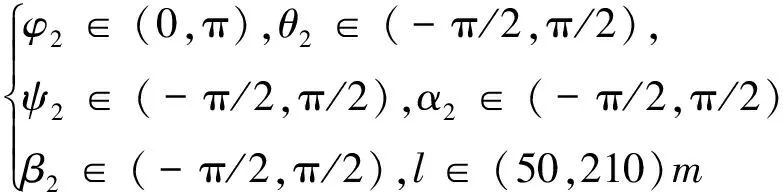
(4)
控制器设计的目标是设计控制律u,使得
(5)
且控制过程中状态q满足约束
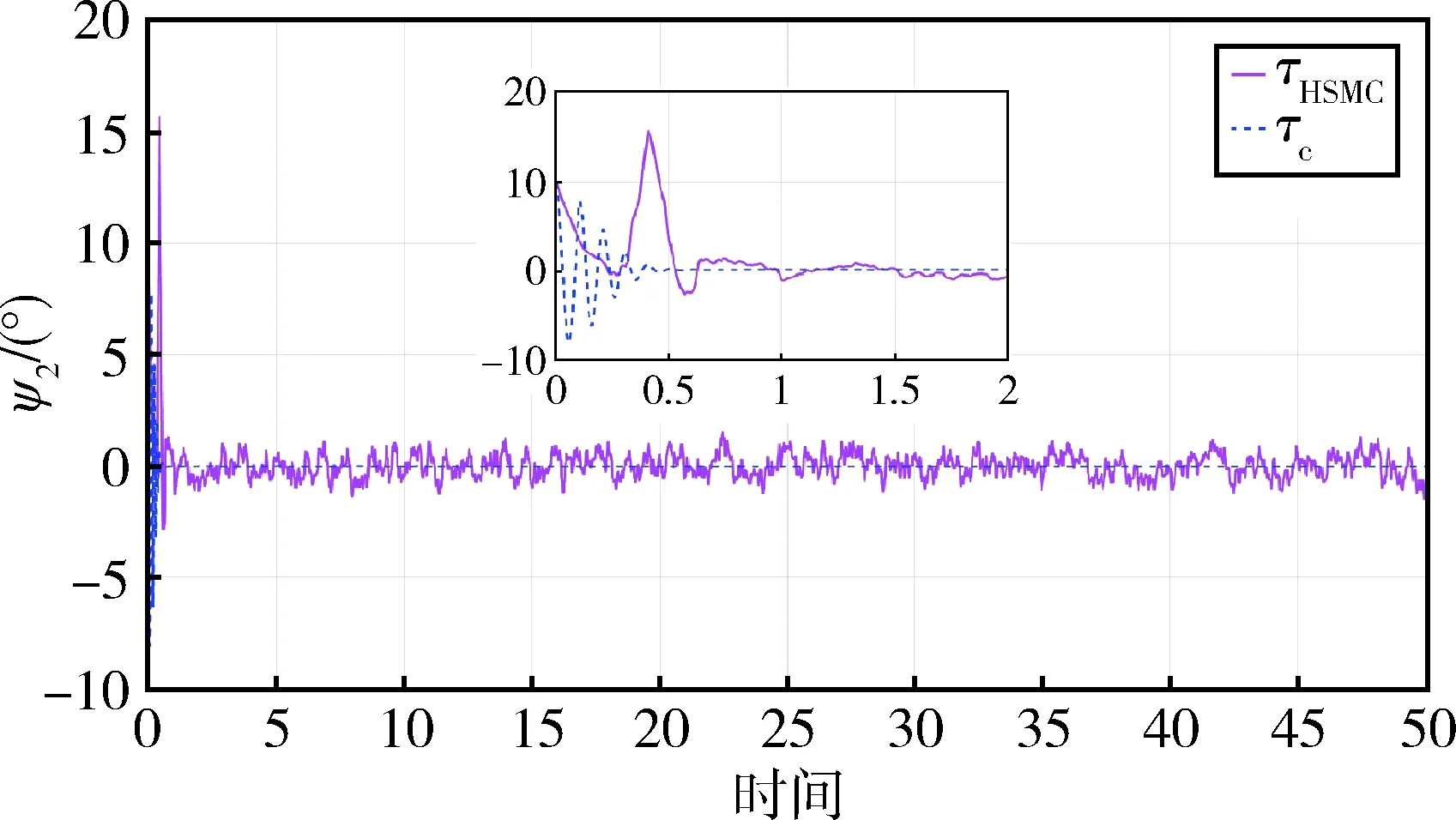
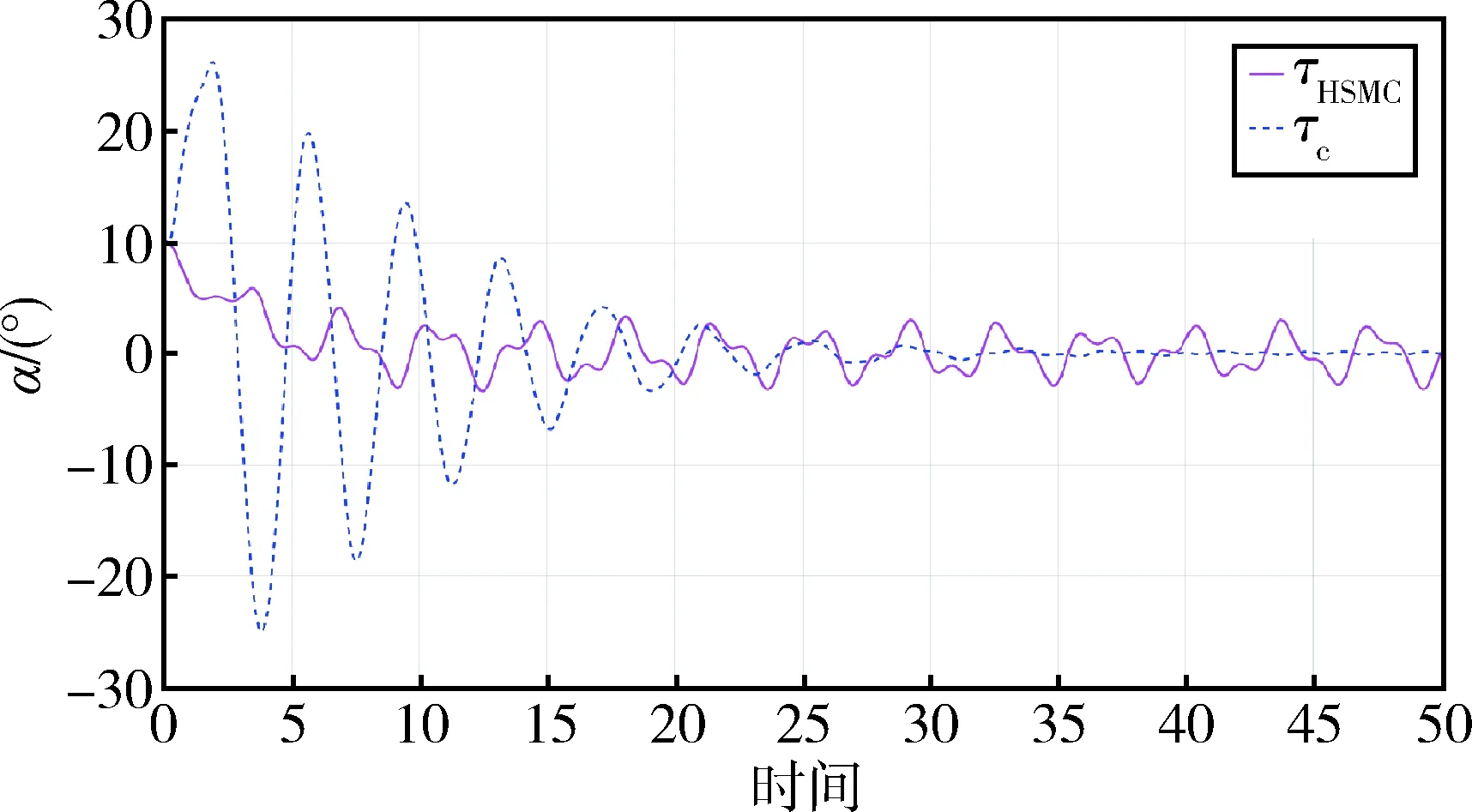
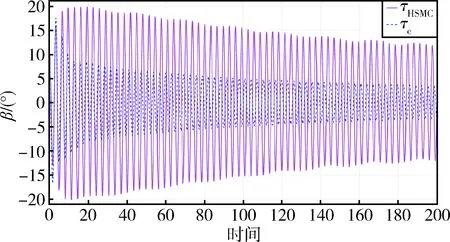
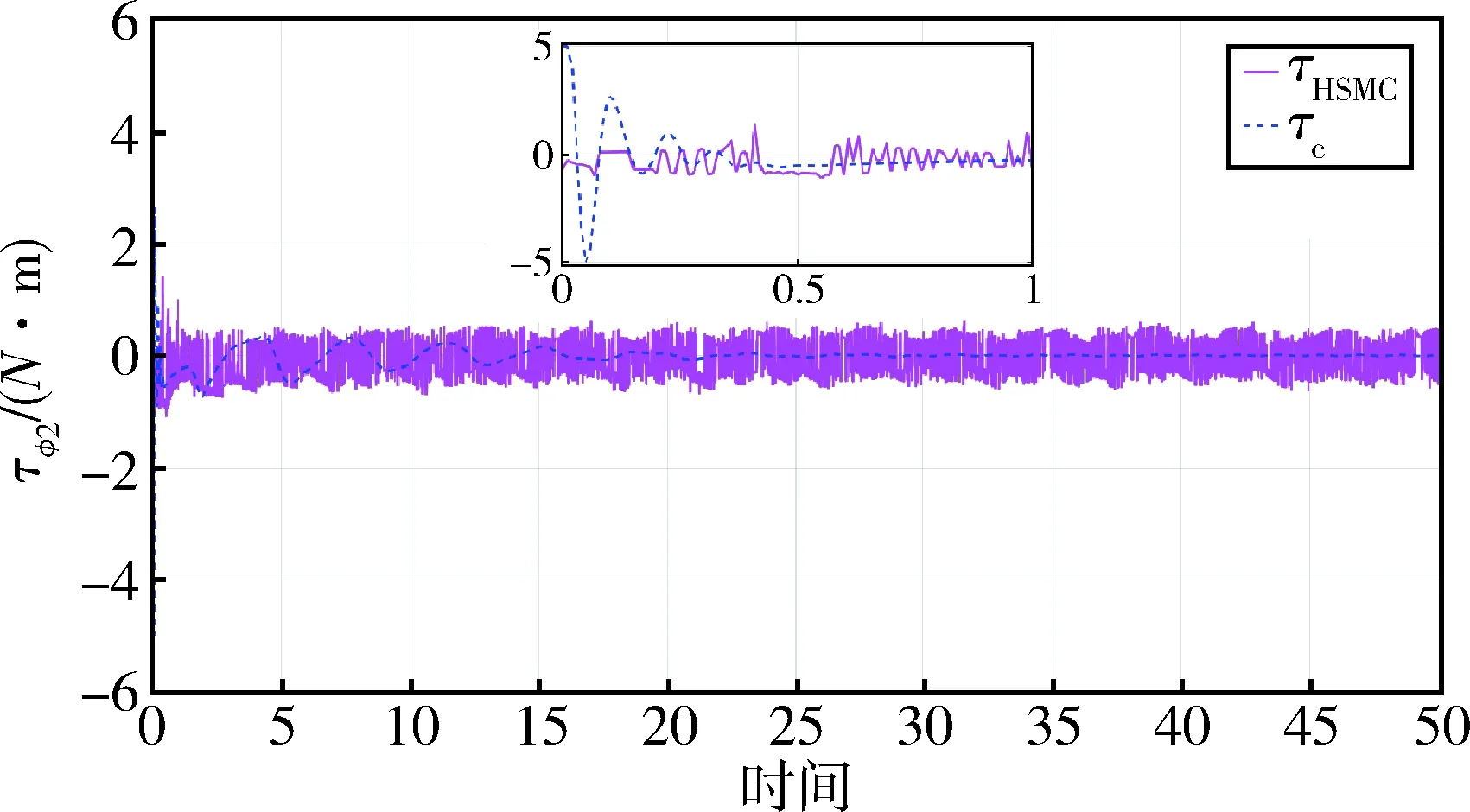
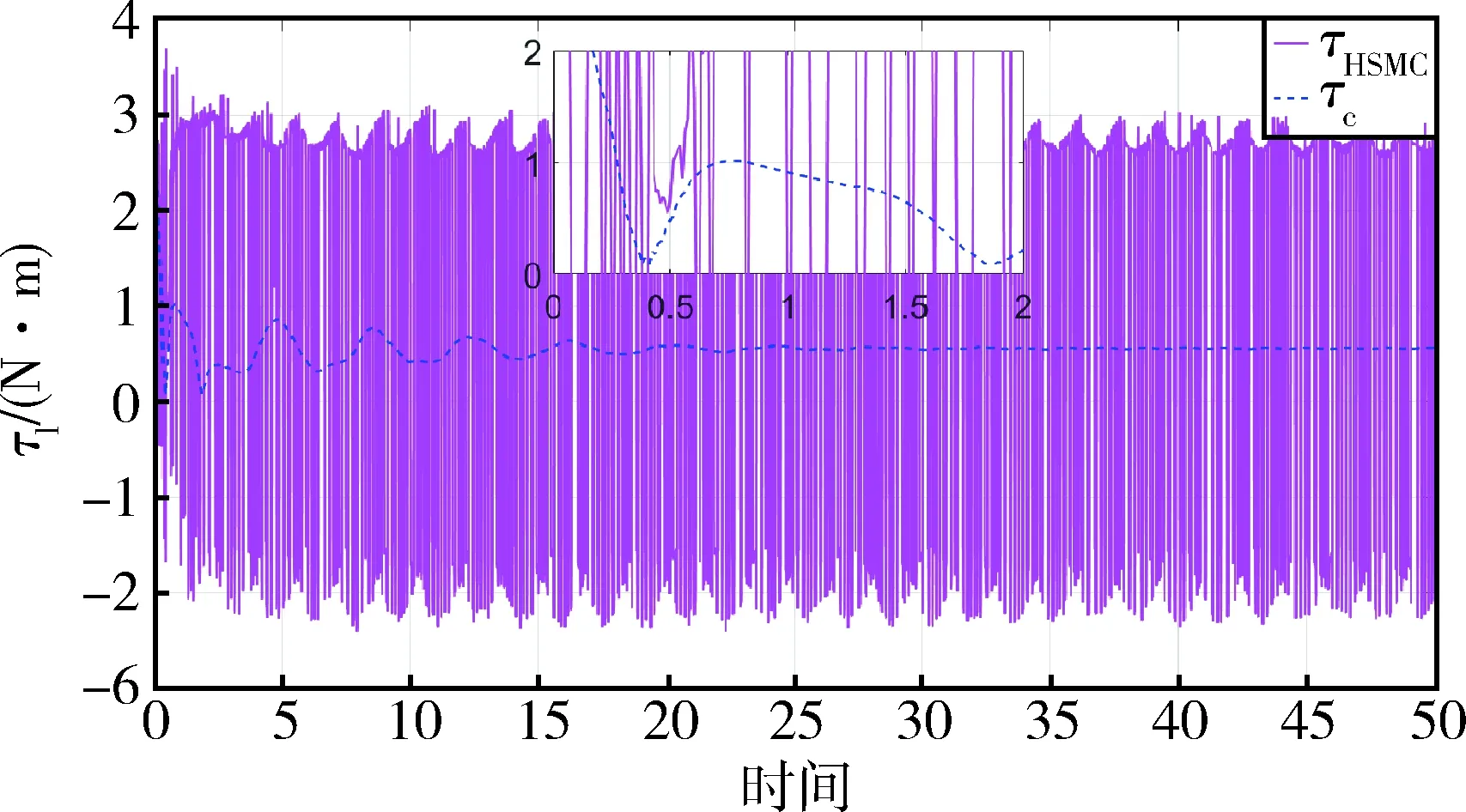
qim (6) 式中,qim和qiM分别是状态量qi(t)的下界和上界. 由系统动力学模型(式)可以得到下式 (7) 式中,Ma,Ca∈Rm×m,Cu∈Rm×(n-m),Ga∈Rm, (8) 式中,Ma为正定矩阵[17]. 首先构造能量函数为 (9) 显然,Es(t)非负,对其求导可得 (10) 然后,定义误差向量为: ea=qa-qad (11) 误差向量的各分量可表示为 (12) 借鉴文献[16]的思路,设计状态约束辅助函数Δ1、Δ2为 (13) (14) 当qi∈(qim,qiM)时,通过推导可知:Δ1≥0、Δ2≥0. 对Δ1、Δ2求导,得 (15) (16) 针对绳系组合体系统式,构造标量函数为 (17) 式中,kE、kv为正实数,κp∈Rm×m为正定对角矩阵.则,该标量函数为非负标量函数. 对式(7)求导可以得到 (18) 式中 (19) (20) 式中,Im为m×m单位矩阵. 根据式,设计控制律为 (21) 式中,κd1,κd2,κd3∈m×m均为正定对角阵. 控制器稳定性证明分三步: 1)证明控制系统是稳定的; 2)证明当初始状态满足状态约束时,在设计的控制律作用下,系统状态始终满足约束; 3)证明在设计的控制律作用下,系统状态能收敛到期望值. 首先证明控制系统是稳定的. 将控制律代入式可得 (22) 因此,系统是稳定的. 其次,证明当初始状态满足状态约束时,在整个控制过程中状态变量均满足约束. V(t)∈L∞,t∈[0,T) (23) 假设状态量qi(t)在时刻T有离开区间(qim,qiM)的趋势,不妨假设qi(t)从上界qiM离开,即有qi(T)=qiM,由此可得 同时根据V(t)表达式可以得到 这与式(23)矛盾.因此qi(t)不会越过上界qiM,同理qi(t)也不会越过下界qim,所以有qi(t)∈(qim,qiM).因此,在整个控制过程中所有状态量均满足约束. 最后,证明在控制律作用下,状态q可以收敛到期望值qd. (24) 式中,V(0)是V(t)的初值. 当状态初值满足状态约束时,由式(9)、(13)、(14)、(17)和(22)可知 (25) 由Ma正定可以得到A也是正定的,因此控制律计算中不会出现奇异,且u∈L∞. 由式(24)可得 (26) (27) 因此可以得到[19] (28) 将式(27)和(28)代入式(3)可得 (19) (30) (31) 因此有 (32) 由式(29)和(32)可知,设计的控制律可以使得系统状态收敛到平衡位置. 设绳系组合体系统参数为 m1=5 000 kg,m2=3 200 kg,mt=0.000 5 kg,Rc=6 371 km,Idx=6 300 kg·m2,Idy=6 246 kg·m2,Idz=4 497 kg·m2,b2y=1.6 m,ω0=0.001 033 rad/s. 初始状态为 设绳系组合体期望状态为 控制律τc参数选择为 为了说明本文控制方法的优越性,下面进行仿真分析.将系统模型无量纲化[20-21],并将本文方法与文献[15]的分层滑模控制律τHSMC进行对比.仿真结果中,横轴表示无量纲时间,每1单位无量纲时间实际表示1/2π个轨道周期的时间. 图2 姿态角φ2变化曲线Fig.2 Time responses of state φ2 图3 姿态角θ2变化曲线Fig.3 Time responses of state θ2 图4 姿态角ψ2变化曲线Fig.4 Time responses of state ψ2 图5 面内角α变化曲线Fig.5 Time responses of state α 图2~4给出了在控制器作用下,姿态角φ2,θ2,ψ2的变化曲线.红色实线代表控制律τHSMC,蓝色虚线本文控制律τc.从图2可以看出姿态角φ2在控制律τc作用下经过约0.3的仿真时间收敛到期望值π/2附近,而在控制律τHSMC作用下大约需要5的仿真时间才能收敛到期望值附近,且τc控制精度高于τHSMC.由图3可知,姿态角θ2在两种控制律作用下,τc作用下的稳态误差略小于τHSMC.从图4可知,姿态角ψ2在两控制律作用下均能快速收敛,但在τHSMC作用下姿态角震颤现象明显.从控制过程中三轴姿态角φ2,θ2,ψ2变化幅度来看,τc作用下姿态角变化范围小于控制律τHSMC作用下的,这是由于控制律τc中的状态约束辅助函数起了作用. 图6 面外角β变化曲线Fig.6 Time responses of state β 图7 系绳长度l变化曲线Fig.7 Time responses of state l 图8 控制输入τφ2Fig.8 The control input τφ2 从图5可以看出,面内角α在控制律τc作用下振荡收敛至期望值附近,收敛速度较慢,但控制精度高于τHSMC.由图6可知在两种控制律作用下,面外角β振幅均有衰减的趋势,而在τc作用下振幅衰减更快,大约经过100/2π个轨道周期的时间后,面外角振幅由初始的10°衰减至5°.由图7可知在τc作用下系绳长度l收敛速度和稳态误差均优于控制律τHSMC. 图8~11为控制输入曲线,红色实线代表控制律τHSMC,蓝色虚线代表本文控制律.从图8可以看出,τHSMC中,τφ2变化范围为[-2,2]N·m,且存在剧烈的抖振现象,而τc中,在控制开始的一段时间内需要较大的τφ2,这是由于控制律τc设计中状态约束辅助函数的引入导致的,当控制一段时间后,τφ2变化范围减小,且变化平稳无抖振现象.由图9可知,τHSMC中,τθ2虽然变化范围较小,但是抖振严重,而控制律τc中,仅在一些时间段内需要较大的τθ2,其余时间则较为平滑.分析图10的仿真结果可以得到与图8类似的结论.由图11可知,控制律τHSMC中,τl存在张力为负的情形,且抖振剧烈,而在控制律τc中,系绳张力τl始终为正,且变化平稳.综上所述,在控制律τc作用下,捕获后组合体系统可以实现稳定,且系绳张力恒大于0,并保证系统状态约束. 图9 控制输入τθ2Fig.9 The control input τθ2 图10 控制输入τψ2Fig.10 The control input τψ2 图11 控制输入τlFig.11 The control input τl 针对绳系机器人抓捕失稳目标星后的欠驱动控制问题,为避免系绳缠绕,本文重点研究了状态严格约束下的稳定控制问题,基于能量法的控制框架,提出了一种加入状态约束辅助函数的欠驱动控制方法,并从数学上证明了加入控制器后,系统能够满足状态约束要求,稳定且能收敛到期望值.文中给出的仿真实例说明了该方法的有效性.2.2 控制器设计
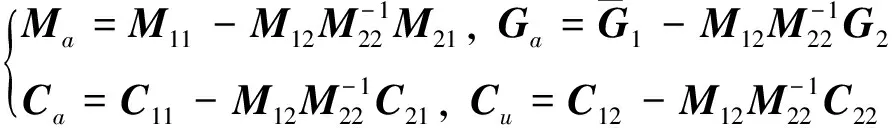
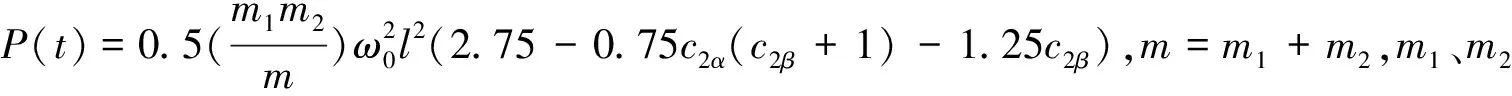


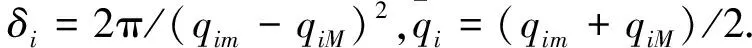
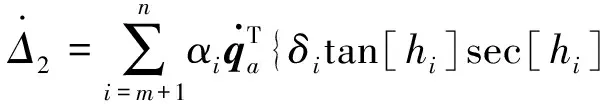
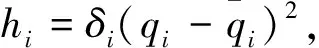
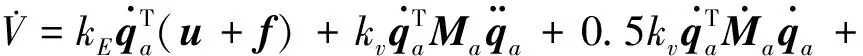

2.2 稳定性分析
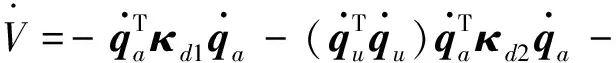

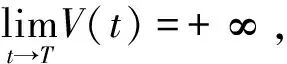
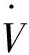
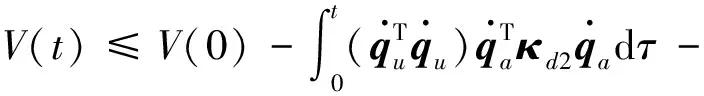
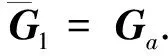
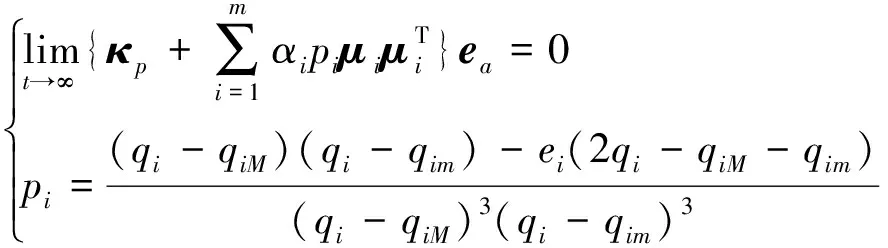
3 仿真验证
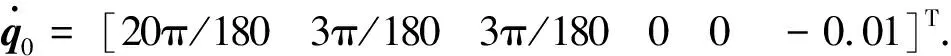





4 结 论

