基于建模优化的连续体机器人轨迹跟踪及扰动抑制策略研究

朱雨琪， 向国菲， 马丛俊， 游星星， 佃松宜

四川大学电气工程学院,成都 610065

0 引 言

近年来，连续体机器人因其固有的内在柔性特性和无穷自由度所带来的与环境友好交互能力而被广泛研究[1-4].不同于刚性机器人的结构化设计，连续体机器人拥有更为丰富的形态智能和柔性特性，可以在狭窄、拥塞等未知非结构化环境下开展自适应作业.然而，如何针对连续体机器人系统设计快速、有效、可靠、精准的控制器，一直是研究领域的热点，具有重要的理论价值和实际意义.

连续体机器人在其驱动方式上有线驱动[5-6]、气驱动[7]、液压驱动[8]等.其中，线驱动连续体机器人结构较为简单，得到最为广泛的研究和应用.文献[9-10]成功将一种细长连续体机器人用于航空发电机零件的检查维修，并开发了一种快速运动学算法.但是，连续体机器人的内在非线性特性和无穷自由度给其控制任务带来了巨大挑战.

针对连续体机器人，其建模思路主要分为以下两种：Cosserat梁理论和分段常曲率假设(piecewise constant curvature, PCC).Cosserat梁理论通过一个非线性常微分方程来描述机器人的张力和形变关系，但因其传感困难，理论复杂，计算成本高，难以协同考虑外部扰动和内部不确定问题，利用该理论建模来完成运动控制任务仍为困难.PCC是目前最为常用的建模策略，通过一组参数集合来表征连续体机器人的状态.在该假设下，连续体机器人的设计[11]、传感[12]、运动学控制问题[13]均已被广泛研究.但是，PCC作为一种对机器人模型的近似，忽略了很多实际的物理因素，仅能得到一个粗略的模型.并且该假设下连续体机器人存在运动奇异点，这将导致机器人的“病态”行为，会给控制器的设计带来挑战.在文献[14]，该团队探讨了连续体机器人在PCC假设的运动奇异问题，并提供了理论解决思路，以一组新的状态参数代替，并在文献[15]中通过自适应控制完成轨迹跟踪任务，虽然解决了运动奇异问题，但是仅在四根驱动线情况下给予建模方法，并且控制策略未考虑计算成本.在PCC假设下，能够得到一个粗略的运动学和动力学模型，这个模型能否提供足够的信息，为后续的控制器设计提供帮助，值得进一步研究.

此外，对于连续体机器人，难以进行精确建模，存在模型误差、参数摄动和未建模动态，另一方面，由于工作环境的未知复杂，对其鲁棒、可靠地控制至关重要.文献[16]首次将鲁棒控制用于连续体机器人，但是仅针对系统内部的小范围不确定性进行设计，无法兼顾外部干扰，需要独立设计其他策略抑制外扰，使得控制效果较为保守.文献[17]使用了基于干扰观测器的控制策略，但是研究重点为考虑不同扰动模型下的效果对比，未能有效结合连续体机器人模型信息、考虑其内部不确定性.基于此，是否存在一种面向连续体机器人的控制策略，能够同时兼顾内部不确定性和外部扰动，并且有效利用已有模型信息，完成其运动控制一直是一个开放性问题，值得我们进一步研究.

自抗扰控制(active disturbance rejection control, ADRC)提供了一种解决思路.该控制方法的主要思路为：首先将系统的内外扰动之和定义为“总扰动”，这之中包括了各种系统未建模动态，外部扰动等不确定因素，并将其进一步定义为系统的扩张状态.设计扩张状态观测器(extended state observer, ESO)，对系统包括“总扰动”在内的状态进行实时在线估计，通过设计非线性反馈控制率，在系统输入端进行补偿[18].传统自抗扰控制由于使用了非线性的扩张状态观测器和非线性反馈策略，在参数调整上面临巨大的工作量，并且理论分析较为困难.高志强教授在此基础上，提出了线性化的方法，通过线性扩张状态观测器(linear extended state observer, LESO)和线性反馈，解决了参数调节问题，并且进一步简化了自抗扰控制的结构，得到了广泛的应用[19].自抗扰控制不依赖于模型信息，但是却能结合已有的模型信息，为控制增益参数的调节提供指导.文献[20]首次将线性自抗扰控制用于解决连续体机器人的耦合问题，提出了一种新的控制思路，但是未考虑机器人运动奇异问题，没有有效结合模型信息，也未能处理好系统初始响应时的峰值问题.

基于上述分析，为解决连续体机器人在存在内扰、外扰等不确定因素时的控制问题，提出了一种能够有效结合模型信息的线性自抗扰控制策略.本文主要工作如下：首先在分段常曲率假设下进行连续体机器人的PCC建模，并进一步优化建模方法以解决运动奇异问题；然后，将系统的模型误差、未建模动态定义为系统内部扰动，和系统外部扰动一同定义为系统的“总扰动”，通过设计线性扩张状态观测器观测器，结合“带宽法”调参策略，实时估计并补偿“总扰动”；接着，为进一步考虑系统初始响应时的峰值问题，并直接利用系统可测输出，减少观测成本，设计了降阶的扩张状态观测器(reduced-order linear extended state observer, RLESO)；最终结合线性反馈，构成整体控制回路，结合已有的模型信息，实现连续体机器人在构型空间的轨迹跟踪控制.

1 问题描述

本文以单段连续体机器人为研究对象，其结构如图1所示.

图1 单段连续体机器人Fig.1 Continuum robot with single segment

该连续体机器人本体弯曲过程产生的力由其内部的柔性支柱提供，并保证其运动过程的灵活度和柔顺性.万向节外壳以铰链机构进行串联，具有体积小、结构稳定的特点.本体内有3根NiTi合金驱动丝，以120°间隔分布，机器人的运动控制由电机转动控制驱动线来完成.

在进行连续体机器人的建模及分析之前，首先给出分段常曲率为建模方法下的假设条件：

1)每根NiTi合金驱动丝的弯曲发生在同一平面，并且曲率相同;

2)忽视机器人本体的重力，仅考虑末端负载;

3)机器人本体柔性支柱长度可发生变化.

1.1 运动学分析

基于分段常曲率法下的连续体机器人建模思路，通常利用一组参数集合来简化其运动学分析，并表征其构型状态，称为曲率参数.

在曲率参数中，φ表示机器人发生弯曲平面间的夹角，称为机器人的旋转角，θ表示机器人的弯曲角，ΔL表示机器人本体柔性支柱发生的长度变化量，通常也可以称为机器人中心轴的长度变化量.通过该参数化方法，可以得到连续体机器人基座到末端的齐次变换矩阵其中s，c，分别表示正余弦函数的缩写，φ,θ∈[-π π].L表示连续体机器人运动时柔性支柱发生形变后的长度，且L=l0+ ΔL，l0表示三根驱动线及柔性支柱初始长度.需要注意的是，当且仅当ΔL≥-l0时才具有实际物理意义.

(1)

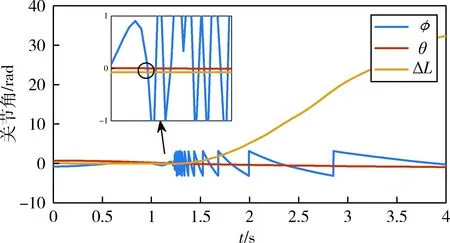
图2 系统输入响应Fig.2 Input response of the system

式(1)包含了连续体机器人末端相对基座的位置和姿态信息，可用于正逆运动学控制.对于基于分段常曲率法的建模思路，通常假设机器人在直立状态下不产生旋转，即不考虑弯曲角θ为0时旋转角φ的取值情况.而实际上，θ为0时，φ可以任意取值.考虑式(2)中平移部分的雅可比矩阵

(2)

其行列式为

(3)

可以发现，当θ→0时，行列式(3)将趋近于0，矩阵(2)会降秩.这个现象反映了在PCC的曲率参数下，若连续体机器人在运动过程中，出现弯曲角θ趋向于0或者是越过0的情况，机器人将产生“病态”行为，并进一步影响系统的稳定性，发生振荡，甚至失去稳定性，如图2所示，在曲率参数下机器人的弯曲角越过0时，引起了系统的参数振荡.

1.2 改进状态参数

为解决连续体机器人在直立状态下的运动奇异问题，提出了一种改进的状态参数，优化曲率参数，以替换传统的曲率参数.图3(a)为曲率参数下的单段连续体机器人示意图.考虑图3(a)中3根NiTi合金丝所连接的{O0}和{O1}两个平面，其中，d表示3根驱动丝连接孔围成的圆的半径，δi为第i根驱动丝在末端平面连接孔处与中轴线的距离，如图3(b)所示，其表达式为

(4)

考虑图3(a)中机器人的弯曲过程，li=θ(L/θ-δi) 表示当前每根驱动线的长度，其表达式为

(5)

通过对li进行简单的代数运算，便可以得到优化曲率参数

(6)

式(6)中的Δx，Δy表示优化后的连续体机器人构型参数，以取代传统使用的弯曲角和旋转角.因连续体机器人的运动奇异问题与参数ΔL无关，所以保留ΔL，这三个参数共同构成新的优化曲率参数集合.图4为优化曲率参数后，连续体机器人的各空间映射.

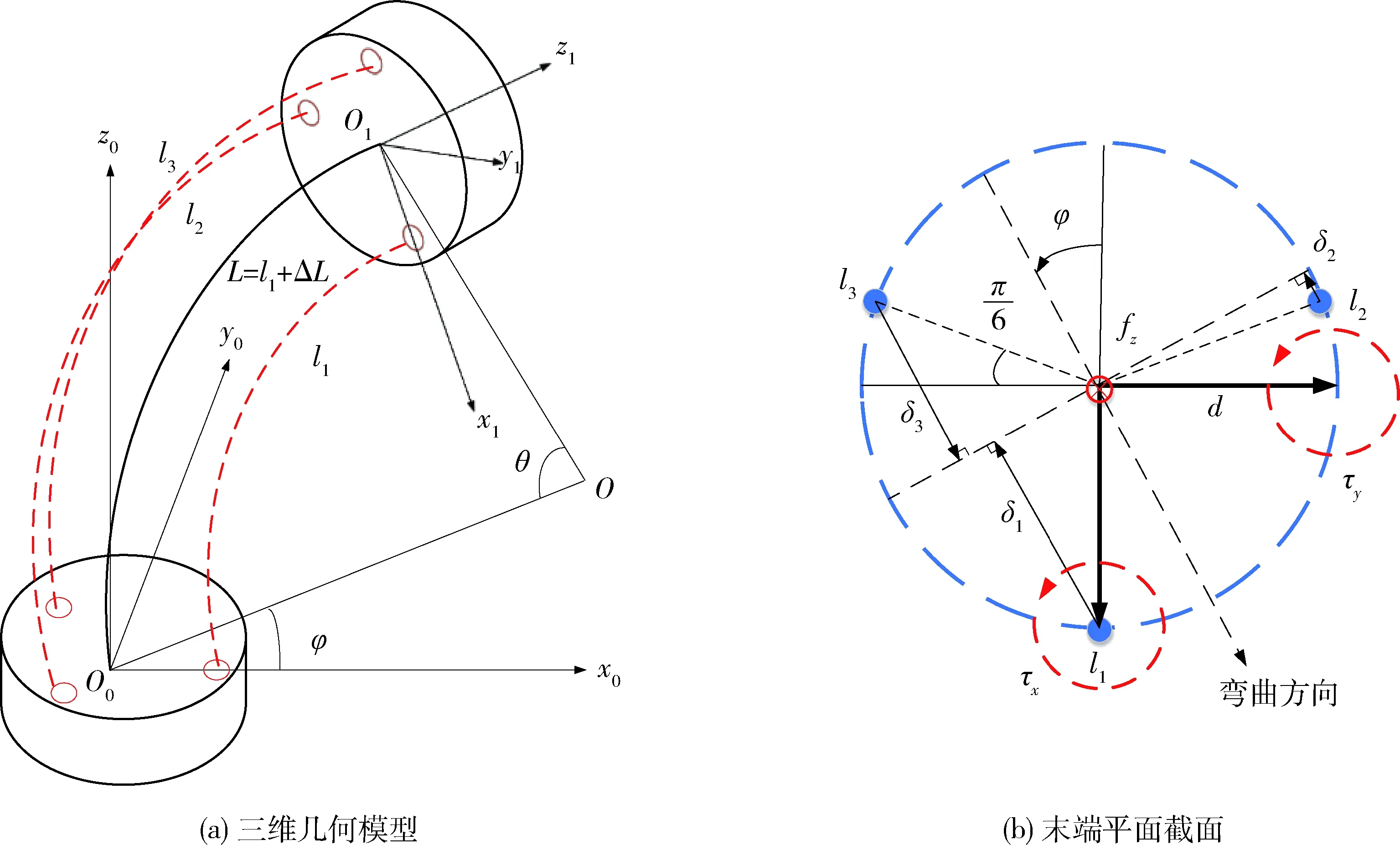
图3 连续体机器人几何模型Fig.3 Geometric model of continuum robot

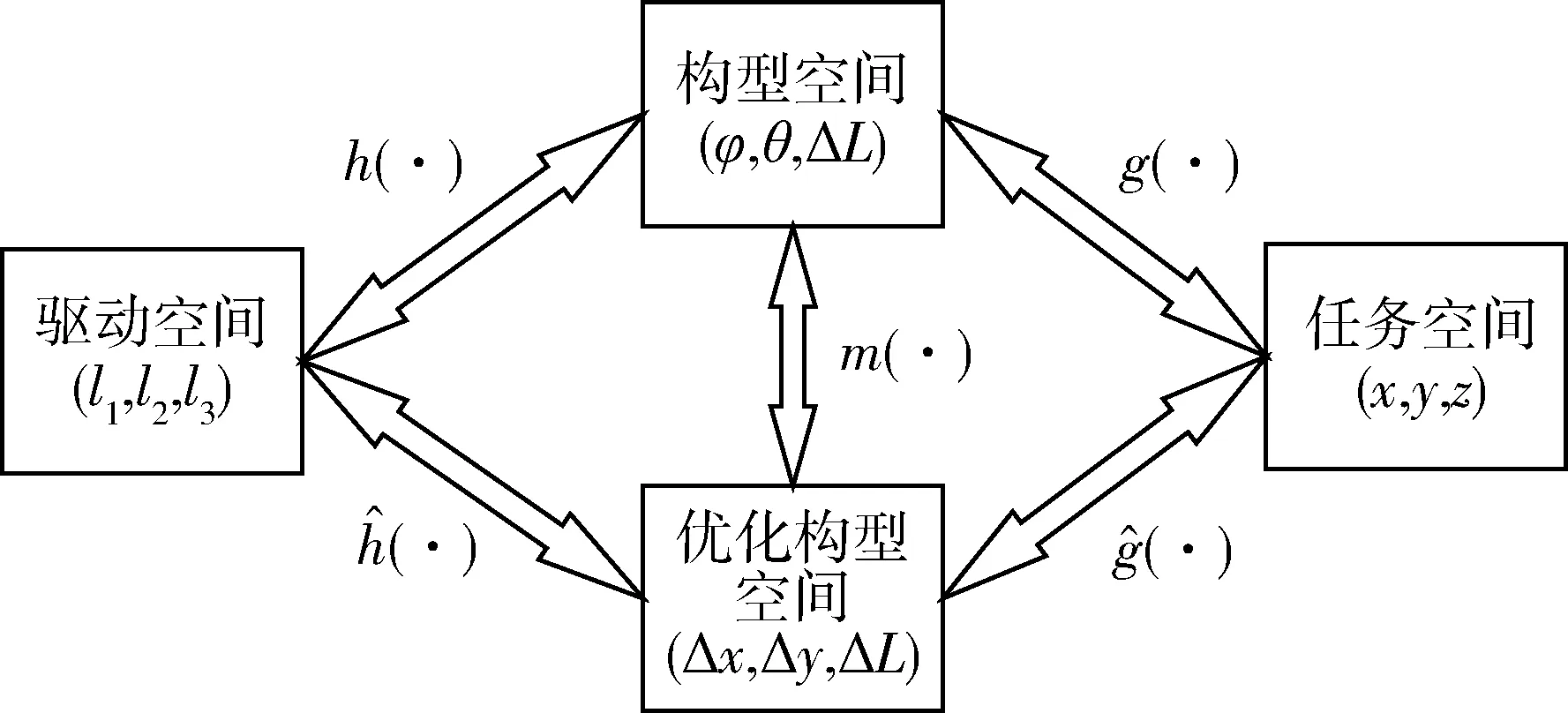
图4 连续体机器人空间映射关系Fig.4 Mappings between each space

在优化曲率参数下，Δx=Δy=0对应曲率参数中的θ=0情况，即连续体机器人直立状态.由此，两种曲率参数之间的映射关系m(·)如下：

(7)

在优化曲率参数下，连续体机器人从基座到末端的齐次变换矩阵为

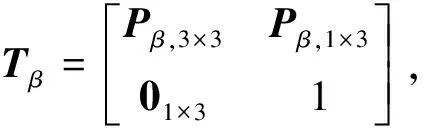
(8)

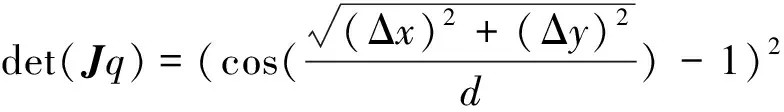
(9)

当(Δx)2+(Δy)2→0时，det(Jq)→L2d4/4.可以发现，在连续体机器人直立状态下，矩阵(8)能够保持满秩.

基于以上分析，连续体机器人在直立状态时的运动奇异问题可以由优化曲率参数解决，并且优化前后的曲率参数之间的代数关系可逆.

注1.图4表示了PCC假设下连续体机器人的各空间映射关系，其中的从驱动空间到构型空间再到任务空间为连续体机器人的正运动学，即h(·) →g(·)，反之为逆运动学.由于m(·)的可逆性，优化曲率参数的引入可以在解决运动奇异问题上建立新的正逆运动学，并且不会影响原正逆运动学.

1.3 动力学分析

连续体机器人的精确动力学建模及其困难，在分段常曲率假设下，仅能建立一个拉格朗日形式的粗略动力学模型[21-22].考虑改进后的优化曲率参数，可以得到如下的动力学模型：

(10)

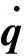
假设连续体机器人末端负载μkg物体，不考虑其本身重力，则惯性矩阵Bβ(q)=μ(JqTJq)，且

(11)

当系统趋近于奇异点时，惯性矩阵Bβ仍满秩.考虑到机器人的无限自由度，为节省建模成本，科氏力矩阵根据反对称性简化计算[23]

(12)

文献[24-25]给出了线性阻抗矩阵和阻尼矩阵的形式

(13)

(14)

且均为满秩对角矩阵.

线驱动连续体机器人通过控制驱动线的变化量以驱动机器人运动，故在末端无法提供能独立产生加速度的力.式(10)中通过输入映射矩阵Aβ联系了驱动线变化量和末端扭矩的关系，为了匹配3根驱动线的独立驱动量，假设末端产生3种独立的力，即u=[τxτyfz]T，如图2(b)所示.Aβ的计算可以根据齐次变换矩阵的雅可比矩阵得到，即Aβ(q)=Ji-Ji-1.Ji表示第i段连续体机器人的雅可比矩阵，且

(15)

若Aβ满秩，则该系统可看作全驱系统.

2 控制器设计

基于以上分析，可以得到一个改进后的连续体机器人动力学模型，但是同时存在模型误差和参数摄动等内部不确定性和外部扰动问题.在这一节，本文将基于线性自抗扰控制提出针对连续体机器人构型空间轨迹跟踪控制的扰动抑制策略.

2.1 线性自抗扰控制

考虑系统内部参数摄动和模型误差，即

(16)

其中ΔB、ΔC、ΔD、ΔK表示系统参数的不确定项，同时考虑外部时变扰动，系统动力学模型式(10)可写为：

(17)

其中d(t)表示时变扰动.进一步将上式改写

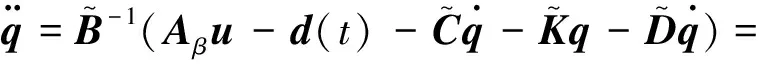
(18)

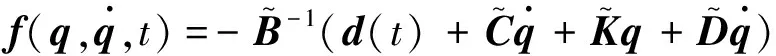
式(18)可看作系统的“标准型”，若能通过相应的观测器设计，实时观测并在输入端补偿“总扰动”，式(18)即可看作拥有严格积分形式的二阶系统，可以任意配置极点[26].为观测并补偿“总扰动”，设计线性扩张状态观测器为

(19)

其中，σ1、σ2、σ3分别表示对系统状态及其导数和“总扰动”的估计.α1、α2、α3和ε均为待调节观测器参数.

定理1.对线性扩张状态观测器(19)，当ε>0、α1、α2、α3为正数且多项式s3+α1s2+α2s+α3满足Hurwitz，观测误差渐进收敛，即

证明. 考虑观测器误差向量如下：

ξ=[ξ1ξ2ξ3]T

(20)

其中

进一步可得

(21)

式(21)可改写为观测器误差方程

(22)

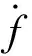
(23)

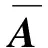
(24)

根据上式可得

(λ+α1)λ2+α3+α2λ=λ3+α1λ2+α2λ+α3=0

(25)

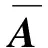
利用线性扩张状态观测器(19)，将系统的“总扰动”定义为扩张阶，并实时观测系统包含“总扰动”在内的所有状态，基于此观测并补偿“总扰动”，可利用线性反馈的方式设计控制器

(26)

其中，k1，k2为待调节线性反馈增益，qref为参考输入信号.将控制器(26)代入系统模型(18)

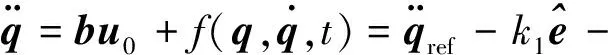
(27)

进一步，得到系统的误差方程

(28)

由定理1可知，观测器的状态能够渐进收敛到系统的实际状态，并完全观测“总扰动”，即，对方程(28),仅需通过合适的反馈增益选取，可保证跟踪误差渐进收敛.

注2.线性扩张状态观测器(19)和线性反馈控制器(26)共同构成了线性自抗扰控制，观测器和控制器的参数可以独立调节，根据文[19]中的“带宽法”，可将参数归为观测器和控制器的带宽调节，仅需要调节2个参数矩阵，即两者带宽，来获得需要的性能.

注3.除观测器和控制器增益外，传统的自抗扰控制仍需要调节控制增益b.一般地，自抗扰控制被认为是“无模型”控制策略，但是增益b难以调节，尤其针对MIMO系统，不同通路之间的增益不同，更有耦合现象难以处理.本文首先求取了连续体机器人的动力学模型，并尽可能利用模型信息，即利用了惯性矩阵作为控制增益矩阵b，与实际的误差通过控制律弥补，既有效利用了模型信息，又减少了调参成本.

2.2 降阶线性扩张状态观测器

线性自抗扰控制由于系统状态初值和观测器初值的差值，往往会在初始响应时造成过大的超调，即峰值现象.为解决峰值现象，平滑系统的初始响应，文献[27]通过先投入ESO，等待峰值现象过后再投入控制，但是这延长了调节时间；文献[28]采用自适应ε参数调节，但是没有较好的调参指导；文献[29]提出使用时变ESO增益，仍面临调参问题；文献[30]提出使用降维ESO，对二阶系统，仅估计速度信号和“总扰动”，通过对观测到的速度信号进行积分获得位置信号，但这对于系统速度的观测有要求，并会造成累计误差.

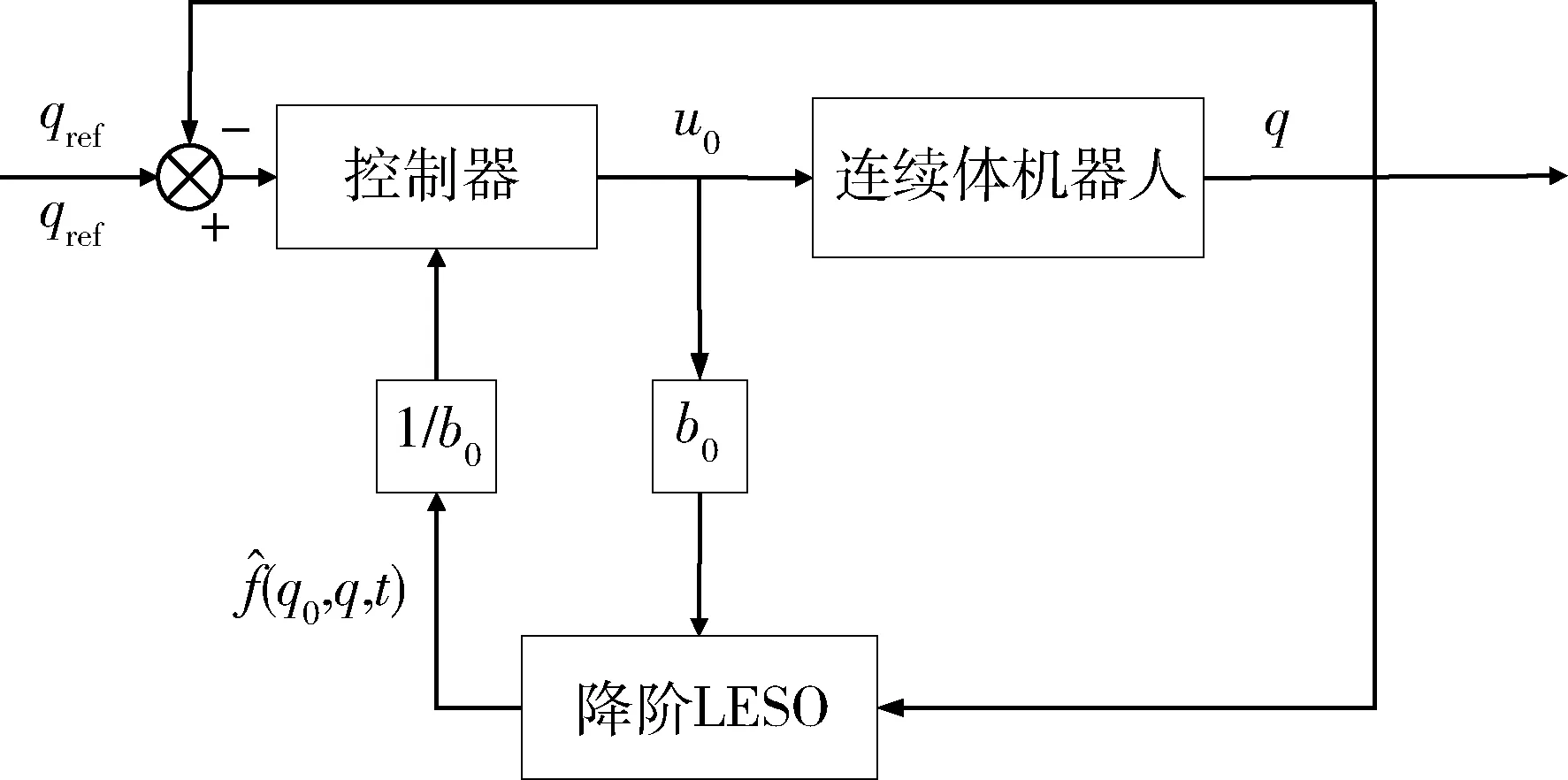
图5 控制框图Fig.5 Block diagram

基于上述分析，本文提出降阶线性扩张状态观测器，以直接利用系统可观测的位置信号，仅估计速度信号和“总扰动”，平滑系统的初始响应，减少峰值现象的影响.图5为基于降阶线性扩张状态观测器的连续体机器人控制框图.

对于观测器(19)，可得降维形式

(29)

(30)

引入变量η2和η3，令

(31)

则式(30)可改写为

(32)

进一步可得

(33)

其中，η2+qα1/ε为速度信号的估计，η3+qα2/ε2为“总扰动”的估计.

基于降阶线性扩张状态观测器(32)的线性反馈控制器设计如下，将观测器与参考信号的位置误差替换为可观测系统输出与参考信号的误差以提升初始响应性能.该观测器收敛性证明与定理1证明思路一致，故不再证明.

(34)

3 数值实例

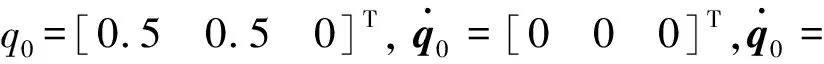
(35)

图6和图7分别为系统位置和速度跟踪效果图.结果表明，滑模控制(sliding mode control, SMC)、LADRC和基于RLESO的LADRC均能实现连续体机器人的轨迹跟踪任务，并能抑制内外扰动.但是SMC由于切换函数的存在，对抗大干扰需要较高的切换增益，会导致系统产生抖振现象，而这对于连续体机器人会加重其末端振动，引起控制器失效.

相较于LESO，RLESO有效处理了系统初始响应时的峰值问题，并减少了调节时间，更快跟踪到目标轨迹.图8为三种控制策略的控制输入，可以发现，LADRC相较于SMC更能有效利用输入资源，无输入抖振现象.图9为RLESO的“总扰动”估计误差，由于系统存在强非线性，采用线性观测器仅能保证估计误差有界，但是结合线性反馈仍能有效完成轨迹跟踪任务.

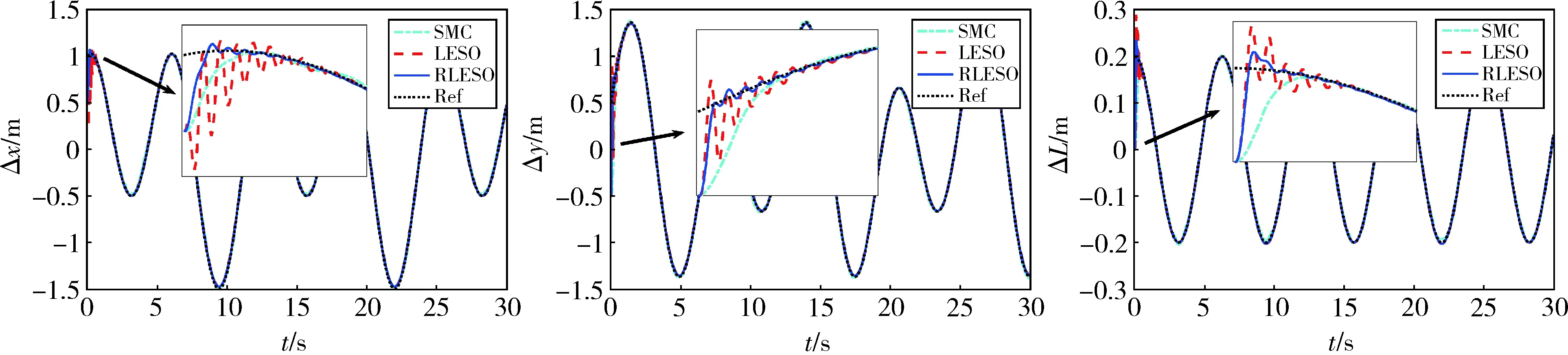
图6 位置跟踪Fig.6 Position tracking

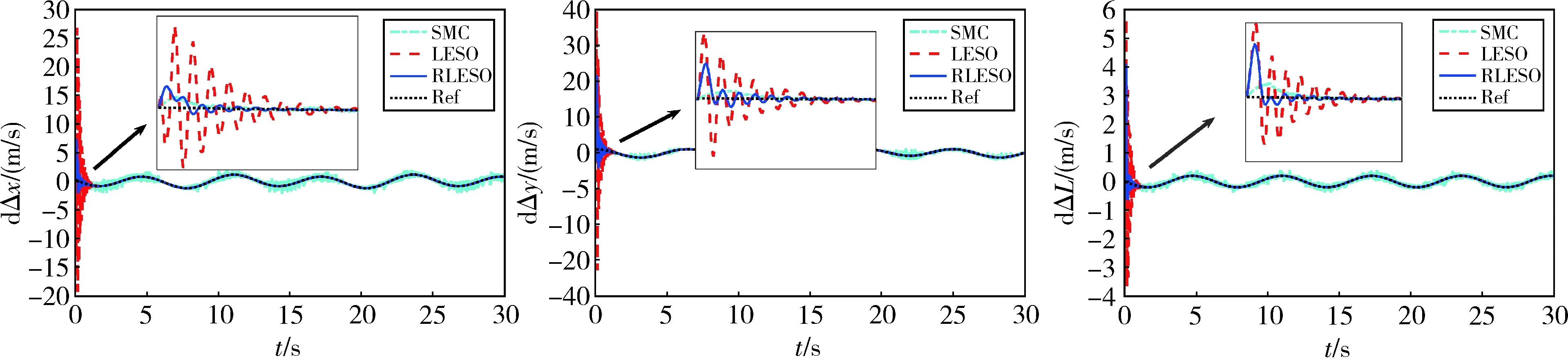
图7 速度跟踪Fig.7 Speed tracking

以上仿真结果表明，对于含有内外不确定性的连续体机器人，采用基于降阶线性扩张状态观测器的自抗扰控制能够有效完成轨迹跟踪任务，且响应速度快，跟踪精度高，能处理系统初始响应时的峰值现象.

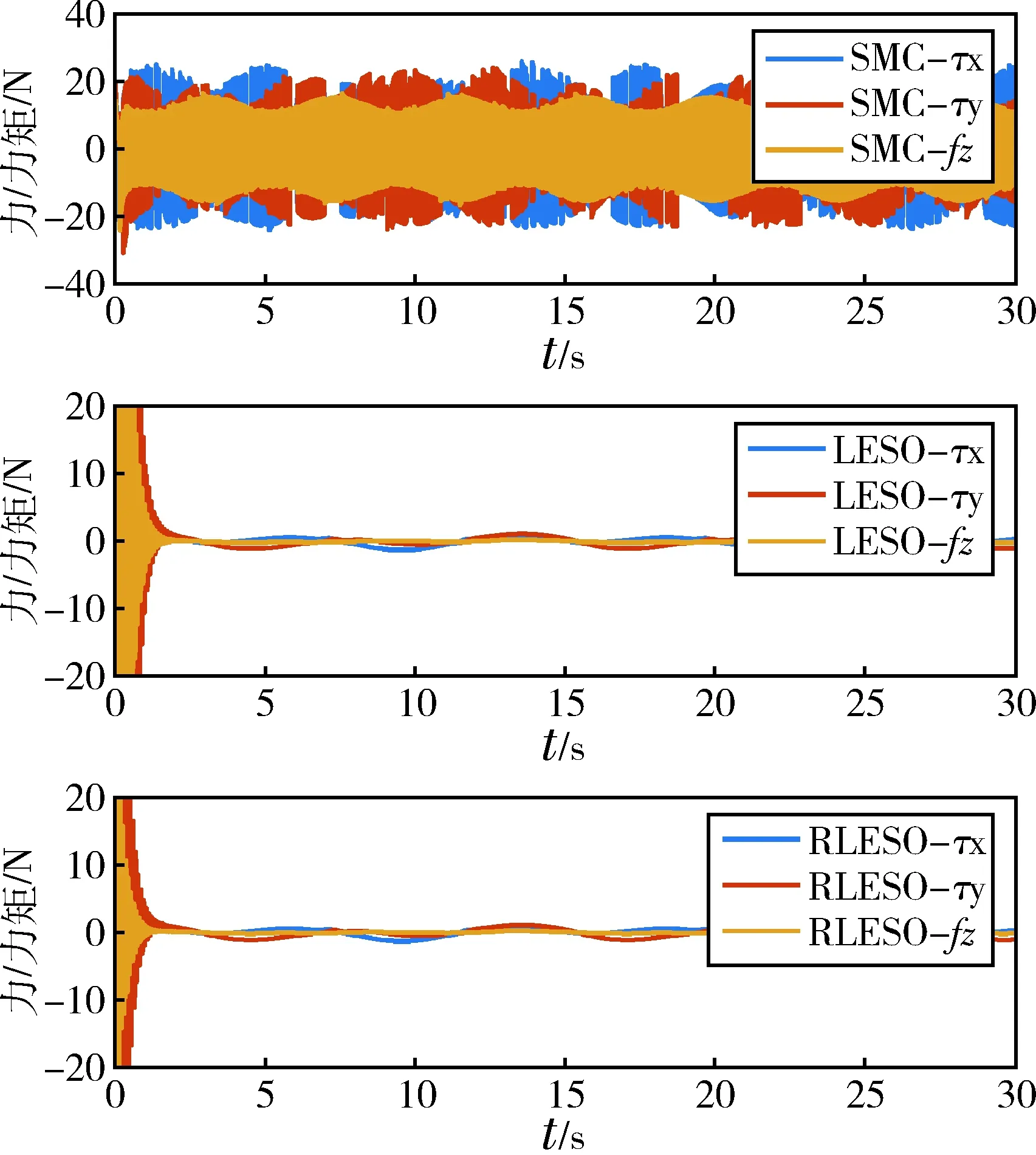
图8 控制输入Fig.8 Control input

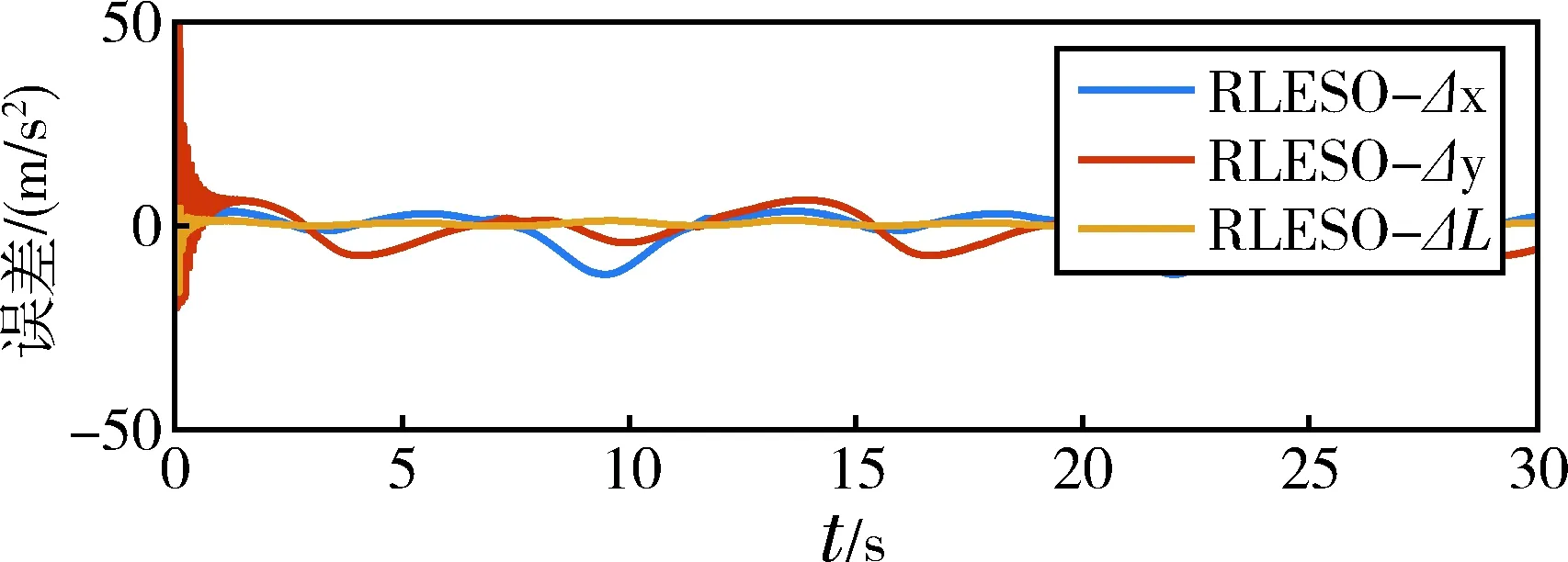
图9 “总扰动”观测误差Fig.9 Errors of the total disturbance observation

4 结 论

针对存在内外扰动等不确定性的连续体机器人的轨迹跟踪问题，本文提出了一种基于线性降阶扩张状态观测器的抗扰控制策略.首先通过提出一组改进的状态参数，解决了连续体机器人在PCC假设下的运动奇异问题，并以此建立了一个近似模型来捕捉机器人的核心动力学特性.通过设计扩张状态观测器实时观测并补偿了包含内外扰动在内的“总扰动”，并进一步设计降阶扩张状态观测器以提升初始响应性能，降低峰值现象.基于Lyapunov稳定性理论证明了其收敛性.设计仿真，综合考虑系统的内部参数摄动和外部扰动，并将本文方法与滑模控制进行对比，结果表明，本文提出的方法跟踪速度快，精度高，能有效抑制内外扰动，降低峰值问题影响.本文提出的方法结构简单，实现成本低，为实现连续体机器人系统的工业应用提供了新的思路.