含有动力学模型误差的星间测量定轨系统能观性分析
周博超, 李 勇
钱学森空间技术实验室,北京 100094
0 引 言
卫星自主轨道确定是指卫星不依赖地面支持,仅利用星载测量设备得到的数据对卫星的轨道参数的估计或计算, 而当动力学建模中存在误差时会显著影响自主定轨的精度.
对于模型误差先验信息不足或不准确的情况,可以采用自适应滤波技术或鲁棒滤波技术,如强跟踪滤波器[1-2],自适应滤波[3-4],基于神经网络的滤波算法[5-6]等.但是,这些算法主要是增强算法的自适应能力,对于常值偏差及可以视为分段常值的慢时变误差这种统计特性比较清楚的情况,采用将偏差扩增为状态进行估计的方式能够得到更好的估计效果.如约化动力学方法通过引入一个过程噪声向量来表示施加于用户卫星上的一个假设的三维力,并将其与状态同时进行估计[7-8].但该方法在测量较少时因不满足能观性而失败,故需要对包含了未知模型误差及状态的增广系统进行能观性分析,从而保证估计的有效性.
传统的单卫星导航一般是依赖于地面站或全球导航星座系统,而对于多颗卫星构成的分布式卫星系统,基于星间测量的自主导航系统能够不依赖外部支持,主要通过星间相对测量信息,利用非线性估计理论解算出卫星间的相对运动状态参数和卫星各自的惯性运动参数,具有自主性强、占用资源少等优点.基于星间测量的自主导航按测量方式可分为基于星间测距[9-10],基于相对视线角测量[11-14]和基于星间相对位置矢量测量[15-18]的导航方法.本文主要考虑基于星间位置矢量测量的自主定轨,李勇[17]已证明了存在星间位置矢量测量的两颗星的状态能观性条件.
能观性的概念最初是由Kalman为了解决确定线性系统的问题而引入的,如果系统的状态能被过去的观测唯一确定,则该系统能观.能观性反映了系统利用有限时间的观测量确定系统状态的能力[19].由于卫星自主定轨系统的方程为非线性方程,非线性系统能观性至今仍是控制理论中一个重要且困难的研究问题.传统的能观性分析方法是将其局部线性化、离散化后采用线性时变系统的能观性理论进行分析.但线性化及离散化会使系统能观性发生变化,故HERMANN等针对非线性系统提出了非线性系统的局部能观性理论[20].李勇提出了非线性系统局部k阶能观的概念, 对满足能观性秩条件的情形, 依据其利用的观测量微分的阶次不同进行了更细致的划分, 体现了要唯一确定系统状态所需要的信息量的多寡程度[17].
本文将采用非线性系统的局部k阶弱能观性理论对动力学模型带有系统误差时的双星自主定轨系统的能观性进行分析,推导并证明自主定轨中状态及偏差都能观的条件,最后采用EKF(extended kalman filter)算法对结论进行验证.
1 系统模型
在地心赤道惯性坐标系中,考虑无摄动项的单个卫星轨道动力学方程为
(1)
其中,μ=398 600.44 km3/s2为地球引力常数,r为地心至卫星质心的矢量,r=|r|,|·|表示矢量范数.
考虑含有动力学模型误差的双星系统,以惯性系下卫星的位置、速度矢量为系统的状态变量,系统状态方程为
(2)
卫星A通过搭载一组星敏感器可以测量自身在惯性空间中的姿态,搭载激光或无线电测距仪可以测量卫星A和卫星B间的距离,搭载光学相机可以测量B星在A星本体坐标系中的方位角.则通过坐标转换可以得到惯性空间中B星相对A星的相对位置矢量rBA=rA-rB.于是,系统的观测方程为
y=h(x)+η=rA-rB+η
(3)
其中η是量测噪声.
2 能观性分析
2.1 局部k阶能观性理论
对于自主定轨的非线性系统,Hermann给出了非线性系统的局部能观性的秩条件.h沿f的k阶Lie导数定义为
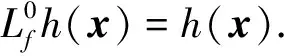
如果在某时刻存在正整数p使得Op(x)=n(其中n为状态维数),则称系统在此时刻的能观性秩条件成立,可以得出结论系统在此处局部弱能观[20].
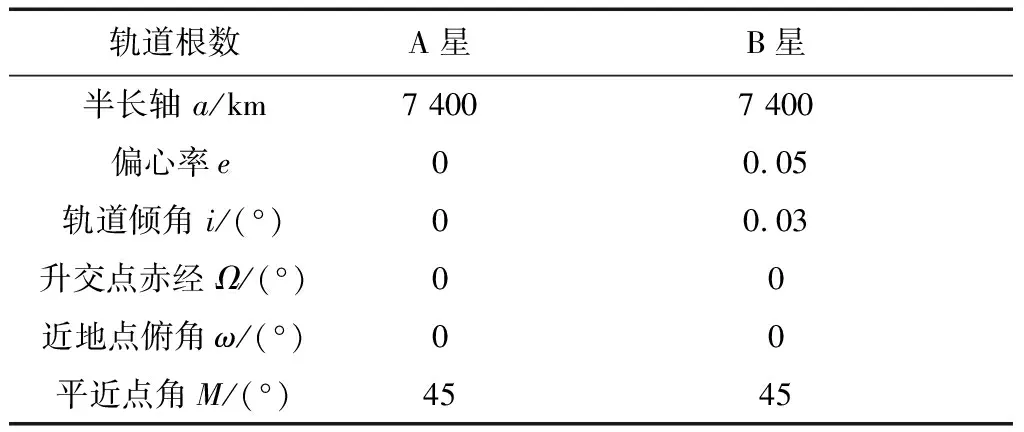
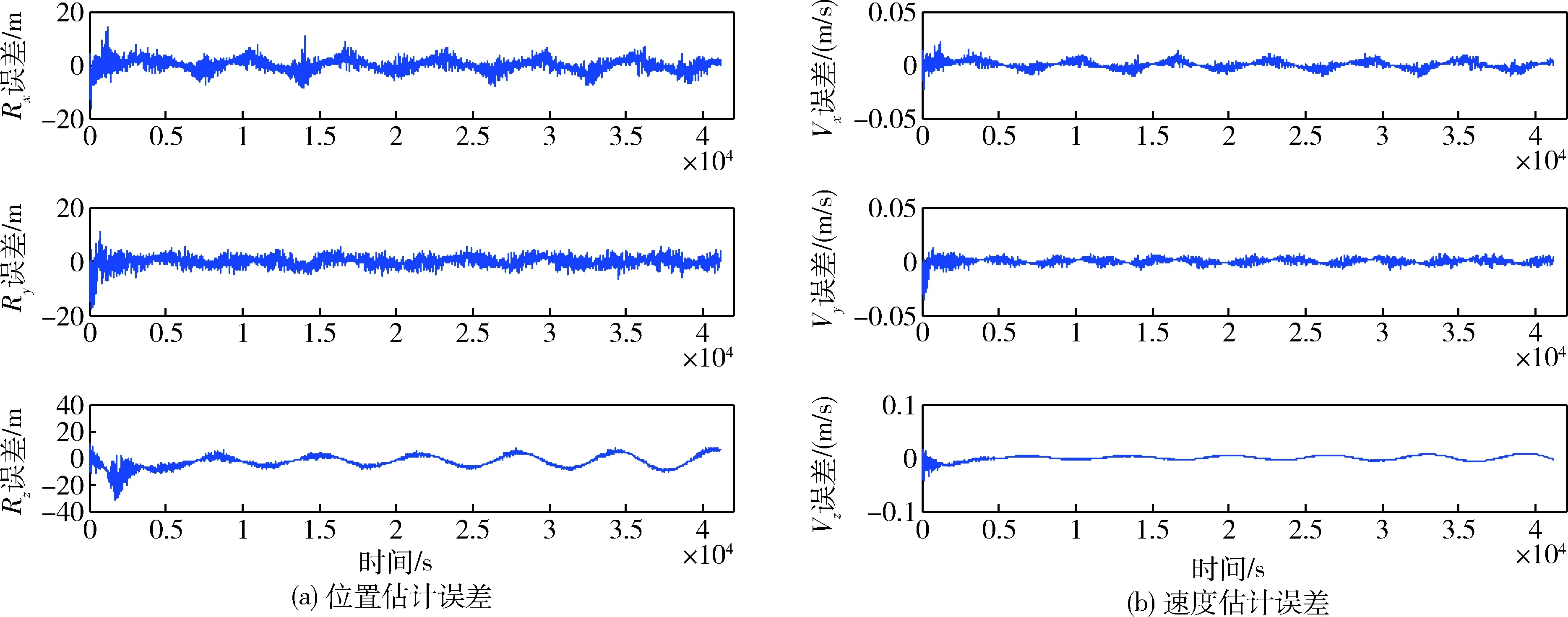
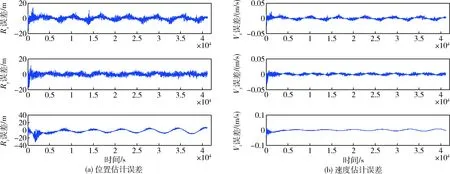
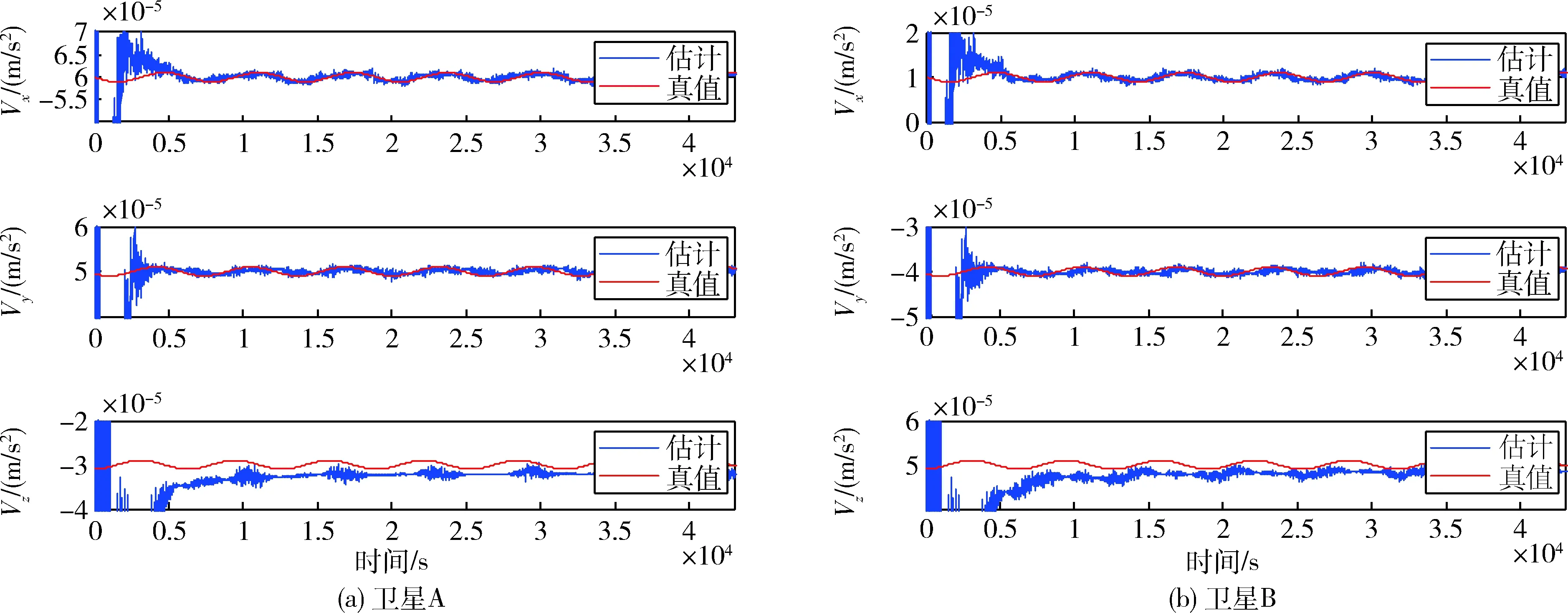
在此基础上李勇提出了非线性系统局部k阶能观的概念, 对满足局部能观性秩条件的情形, 依据其利用的观测量微分的阶次不同进行了更细致的划分[17]:若对于整数k>1,有Ok-1 不考虑两颗星的动力学模型误差时,原系统在t时刻的能观性秩矩阵为[17] 由测量方程式(3)可知该矩阵需要求r的各阶导数,由文献[17],有下面的引理: 引理1.对于模型(1),存在关于u,p,q的常系数多项式函数序列fk,gk(k≥2),使得在r(t)的线性流形上有下式成立 其中 (4) 特别地,有 于是有 下面分析考虑动力学模型误差时的系统能观性,在所考察的瞬时局部可将实际中慢时变的误差近似等效为相应的常值向量,将两个卫星的模型误差及位置、速度矢量共同构成扩维状态量 则不考虑随机噪声时,扩维系统状态方程和观测方程分别为 (5) (6) 扩维系统的Lie导数满足 依此类推,我们有: (7) 故增广系统的能观性秩矩阵为 分析该能观性矩阵的秩,可得如下定理: 定理1.在t时刻,系统(5)和(6)局部弱能观的充要条件为在t时刻uA与uB,pA与pB,qA与qB不全相等. 证明:在t时刻能观性矩阵的秩满足 (a)如果uB≠uA我们有 存在某个k,使得 (8) 此式为关于uA、pA、qA的高阶多项式方程组,以uA、pA、qA作为自变量采用MATLAB符号运算工具求解方程组{sk=0}(k=4~6) 得到的结果为无解析解.即一定存在某个k,使得sk-1≠0,经过一系列的仿真结果也验证了该结论,即uA≠uB时增广系统(5)(6)是局部弱能观的. 综合(a)~(c)可得,t时刻增广系统局部弱能观的充要条件为uA与uB,pA与pB,qA与qB不全相等,证毕. 由式(4)可知,uA与uB,pA与pB,qA与qB全相等意味着rA=rB,vA=vB,rA·vA=rB·vB. 由开普勒轨道的活力方程 当vA=vB,rA=rB时有aA=aB,即两星的半长轴相等. 由二体问题的公式 其中P,Q互相正交,有 于是有 eAcosEA=eBcosEB (9) (10) 由式(10)可得 sinEAeA(eAcosEA-1)=sinEBeB(eBcosEB-1) 将式(9)代入可得 eAsinEA=eBsinEB (11) 由式(9)和(11)可得 tanEA=tanEB或eA=eB=0 由tanEA=tanEB可得EA=kπ+EB.但eA,eB都是非负数,故由式(9)可得一定有EA=2kπ+EB,代回到式(9)可得eA=eB. 综上可得,增广系统不能观的充要条件为 1)aA=aB,eA=eB=0 即两个卫星运行在半长轴相同的圆轨道,此情况下任意时刻都不能观. 或者 2)aA=aB,eA=eB,EA=2kπ+EB,两个卫星运行在半长轴与偏心率都相同的轨道,此情况下,每个轨道周期会出现一次局部不能观的情况. 由于给出的是自主导航系统能观性秩条件成立与否的充要条件, 故而可以用来考察两个卫星轨道特征以判定是否局部弱能观,可以为星间测量定轨系统设计提供参考. 假定状态模型误差与测量噪声均为独立零均值白噪声,且离散化后对应的方差阵分别为Qk,Rk,则基于标准EKF算法,有扩维后系统的滤波方程如下: 1)计算状态一步预测值 数值积分,得到一步预测的扩维状态 2)预测误差方差阵 式中Φk/k-1为状态转移矩阵,可由如下微分方程解得 积分初值为单位阵. 3)增益矩阵 4)状态估值 5)估计误差方差阵 (1)系统误差为常值的情况 仿真场景中,卫星的轨道根数如表1所示,仿真的轨道由二体模型加误差加速度积分而得,即: 表1 仿真卫星轨道根数Tab.1 Orbital Elements of simulated satellites 其中两颗星的误差加速度aA,aB设置为常值偏差,分别为 aA=[6×10-55×10-5-3×10-5]Tm/s2 aB=[1×10-5-4×10-55×10-5]Tm/s2 并且都加上了标准差为10-5m/s2的高斯白噪声. 测量数据为卫星星间位置矢量加上标准差10-2m的白噪声,即 y=rA-rB+η EKF估计初值设置为初始状态加上1 km(位置),1 m/s(速度)的初始误差.仿真时长12 h,估计结果如图1~2所示. 稳定后三轴位置均方误差如表2所示. 从结果可以看出,系统误差为常值偏差时,能够对状态及系统误差进行有效的估计. (2)系统误差为慢时变的情况 在实际中模型误差往往不是常值,将其建模为随卫星轨道周期而缓慢变化的周期慢时变偏差更为接近实际情况.仿真卫星依然如表1所示,轨道仿真中的动力学模型误差设置为以轨道周期T为周期的慢时变系统偏差仿真其余参数不变,结果如图3~5所示. 表2 常值误差仿真结果Tab.2 State estimation results of constant bias case 稳定后三轴位置均方误差如表3所示. 图3 慢时变偏差算例A星估计误差Fig.3 Estimation results of Sat A in slow time-varying bias case 图4 慢时变偏差算例A星估计误差Fig.4 Estimation results of Sat A in slow time-varying bias case 图5 慢时变偏差算例模型误差估计结果Fig.5 Estimation results of unknown accelerations in slow time-varying bias case 表3 慢时变误差仿真结果Tab.3 State estimation results of slow time-varying bias case 从结果可以看出,滤波在一个轨道周期左右即稳定且达到10m以内的精度,说明含有慢时变系统偏差的系统也能够得到准确的估计. 本文针对二体轨道动力学模型,应用非线性系统的局部弱能观性理论分析了存在模型误差时基于星间位置矢量的双星自主定轨系统的能观性,给出了系统对双星各自运动状态及模型误差都能观的充要条件.采用扩维EKF算法设计了自主定轨和偏差估计算法并进行了仿真,仿真结果显示,在满足局部能观的条件下,基于星间位置矢量的双星自主定轨系统对于状态及模型误差的估计是可以满足高精度要求的,无论系统误差为常值或是慢时变的情况.2.2 含模型误差的基于星间矢量测量自主定轨能观性分析
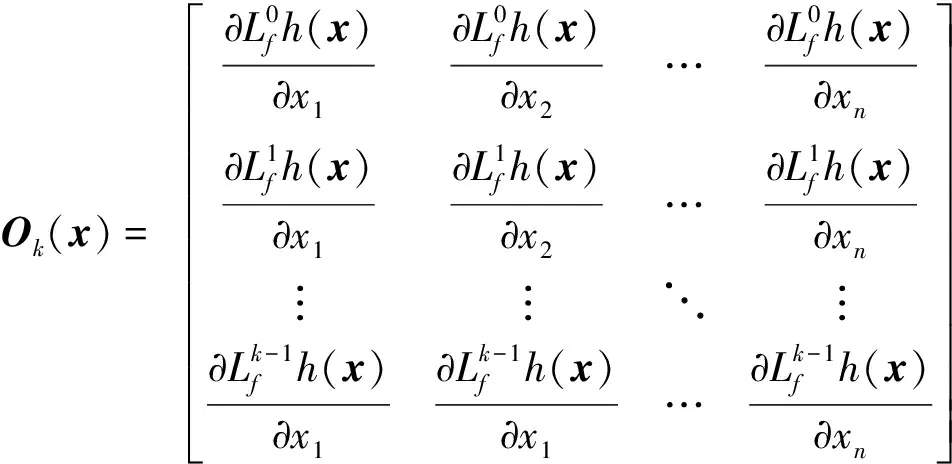
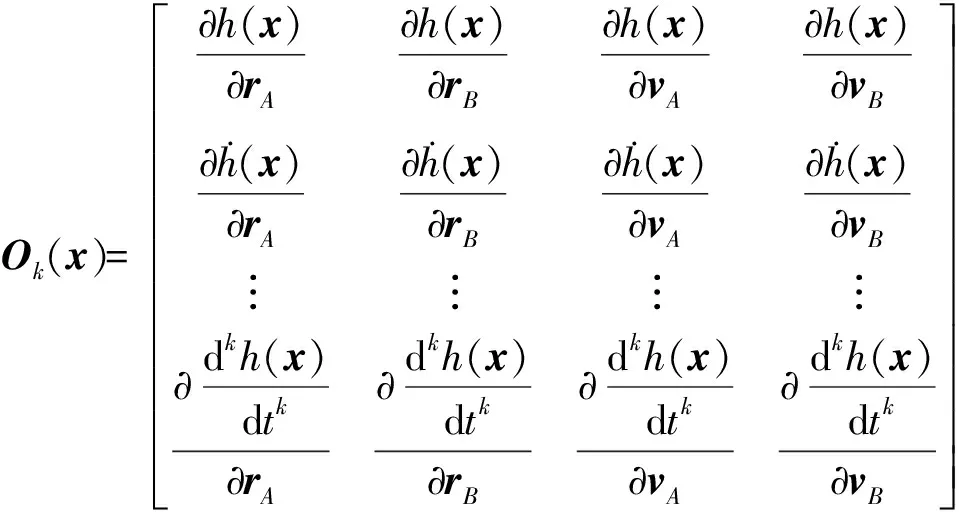
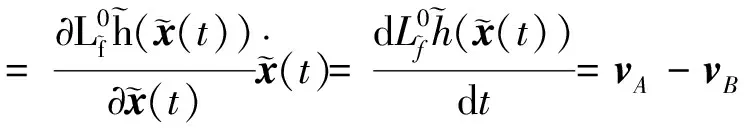
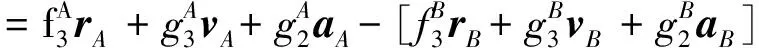
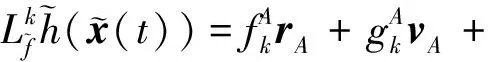

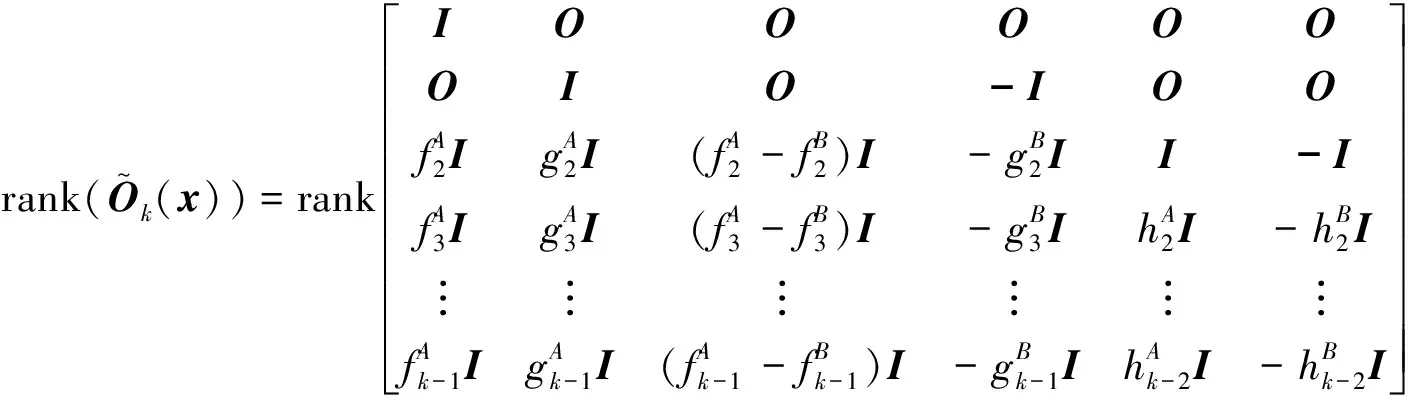
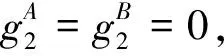
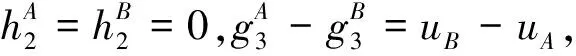
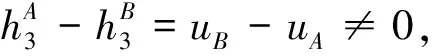
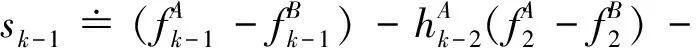
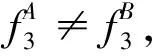
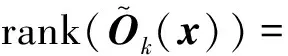
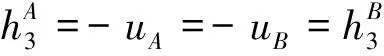
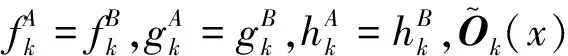

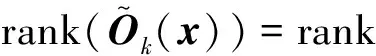

2.3 能观性结论解释
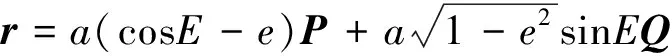

3 估计算法与仿真
3.1 扩展卡尔曼滤波算法
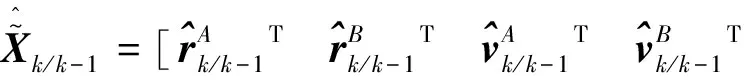
3.2 仿真分析


4 结 论

