一种基于阻抗控制的机械臂双轴孔插孔柔顺控制方法研究

李歆雨， 张 强， 文 闻， 周晓东， 李晓辉

北京控制工程研究所,北京 100094

0 引 言

在轨加注是指通过某种技术手段将推进剂从服务航天器转移到目标航天器从而使目标航天器恢复正常的推进系统功能的服务技术，是多国大力研究发展的具有低成本延长航天器使用寿命能力的重要在轨服务技术.美国“轨道快车”于2007年实现先期技术验证装置升空，进行了自主交会对接、服务星对目标星的捕获对接、燃料输送以及模块更换等技术验证，在在轨加注演示实验中服务卫星向客户星进行了多次燃料往返传输，对其泵传输和压力传输两种方式均进行了全面测试[1-2].美国2011年启动的RRM在轨试验，对不具备专门在轨燃料加注接口的低地球轨道非合作卫星，采用直接传输的方式进行在轨燃料加注[3].我国天舟一号货运飞船与天宫二号空间实验室于2017年首次成功完成推进剂在轨加注实验[4].通过在轨加注技术的实现，可以提高航天器的机动能力，灵活机动增强了目标航天器的灵活性，使其能够完成更多任务；可以增强航天器的航行距离，变相提高航天器推进剂携带能力，有助于深空探测；有助于挽救失效卫星，通过对失效航天器补充燃料可以实现姿态控制、轨道机动等，延长航天器的寿命.同时加注推进器也是对空间站等大型空间平台日常维护不可或缺的项目.

在轨加注过程中，通常需要补充的航天器燃料由燃烧剂和氧化剂两种，因此燃料传输机构具有两个接口，如图1所示，可同时接受燃烧剂和氧化剂注入，传统刚性机械臂位置控制很难同时满足两个轴孔插入的空间要求，为解决这一插孔问题需要针对性设计适用于双轴孔插孔的控制方法.除在轨加注过程之外，双轴孔插孔的控制还适用于一些为保证对接的相对位置姿态采用多个定位销引导对接的对接元件.

图1 对接与流体传输机构Fig.1 Docking and fluid transfer mechanism

插孔过程中在机械臂由自由空间到与环境空间接触的过程中由于尺寸、定位以及运动控制的误差以及机械臂惯性和相应频率等原因可能会造成机械臂末端与对象的刚性碰撞，从而导致空间机器人和操作对象的运动姿态变化或碰撞破坏.为避免这样的误差和破坏对任务造成的负面影响，需要引入对机械臂的柔顺控制.

柔顺控制主要包括阻抗控制、力跟随控制、力位混合控制等的控制算法实现.力位混合控制将空间氛围位控切向和力控法向两个正交空间，分别进行位置控制和力控制，通过在一些自由度上采用力控制，其余自由度采用位置控制，以实现综合控制[5-6].这种控制方法原理简单，相对容易实现，但缺乏机械臂与环境之间动态耦合关系的描述，难以实现力位控制的配合，在复杂现实环境的应用容易造成较大的控制误差.阻抗控制将对象位置偏差与接触作用力之间的关系称为目标阻抗，通过动态调节阻抗来实现柔顺控制[7-9].在实际应用情况下，阻抗控制对于环境的位置、刚度和阻尼等参数提出了很高的要求，即使是很小测量误差都将对力的输出造成很大影响.对于双轴孔插孔的控制问题，由于插孔过程中接触力的大小和方向实时受环境和机械臂多重因素的影响，难以分解到有限的自由度控制，因此选择侧重于描述机械臂与环境柔性交互的阻抗控制方法实现柔顺控制.

本文针对双轴孔插孔控制问题，首先分析双轴孔插孔的插孔过程和接触状态，随后设计一种基于阻抗控制在接触力反馈的作用下实现柔顺插孔过程的阻抗控制器，最后通过仿真实验的方法验证该柔顺控制方法的实用意义.本文提出的柔顺控制方法满足在轨加注、在轨装配等需要同时实现双轴孔配合的空间操作要求，适应于空间在轨服务机械臂遥操作以及智能化操作技术的发展需求.

1 双轴孔插孔的过程和状态分析

在在轨加注过程中，加注主动端固定在机械臂末端，加注口位于目标航天器表面，若期望一对加注口同时插入加注口中，则控制机械臂带动油枪靠近目标加注口，在二者相接触后依据接触力的反馈信息调整机械臂末端姿态，在阻抗控制下机械臂末端具有近似于阻尼弹簧的特性，在贴近的过程中逐渐实现轴孔间的配合.

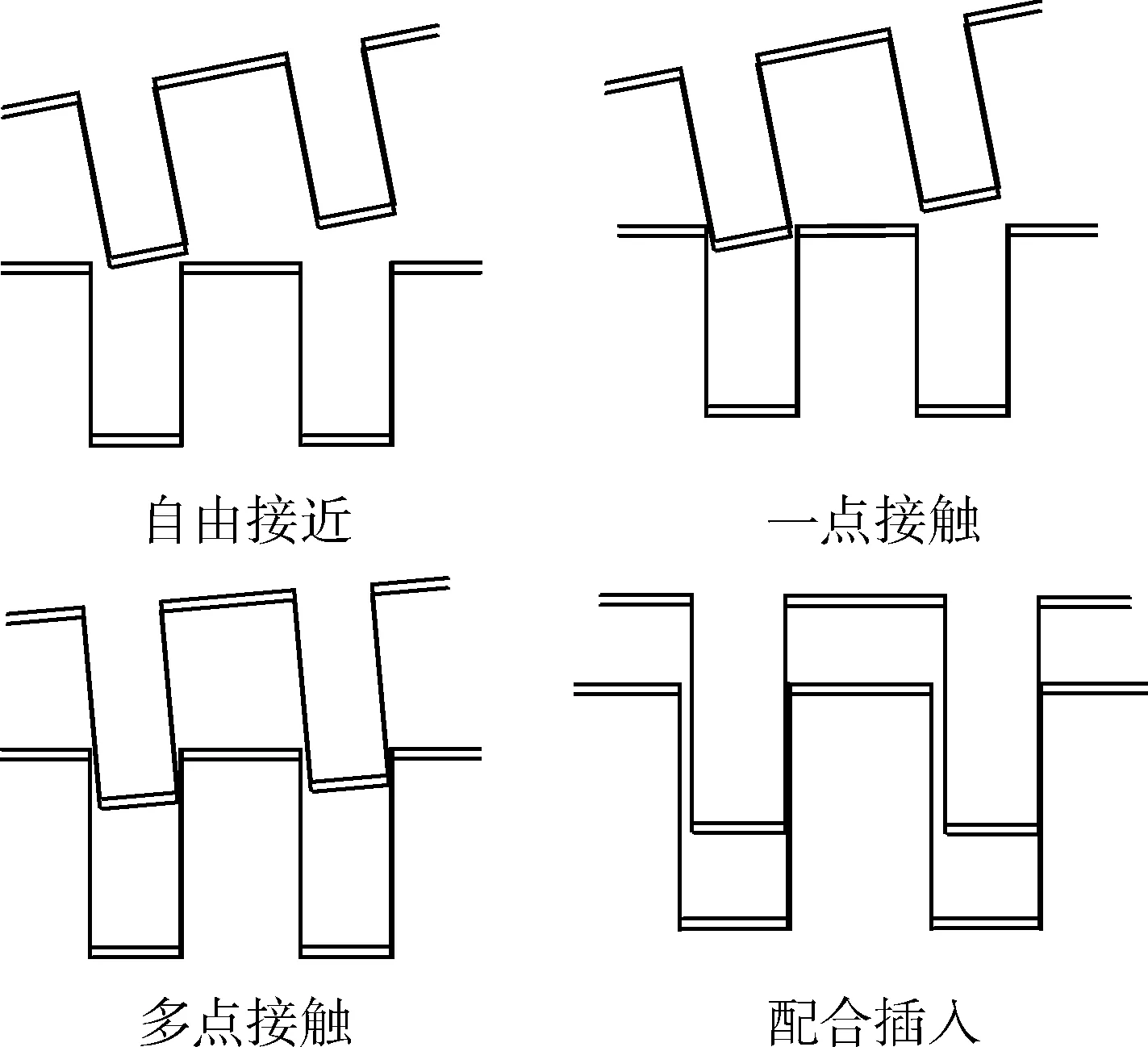
图2 双轴孔插孔过程Fig.2 Double Peg-in-Hole Assembly

通常情况下，双轴孔的插孔过程包括自由接近、一点接触、多点接触、配合插入4个主要过程[10]，如图2所示，对插孔结果起决定性作用是二者接触过程的相对位置姿态.二者接触过程中，通过感应器反馈的作用力和扭矩的值分析二者接触的相对位置姿态，设计进一步的运动趋势，使所有可能的位置状态下轴孔都在较小接触力的作用下朝尽可能减少误差的状态运动.

与单轴孔的插孔过程相比，实现双轴孔插孔面临更复杂的控制要求[11]：首先对于自由接近的初始位姿具有一定要求，只有当轴与孔相接触时的倾斜角θ、插入过程Z轴的扭转角φ以及轴与孔的相对位置关系都限定在一定范围内时才能实现双轴同时插入，这个范围由轴孔的尺寸和装配精度决定，这样的要求对自由接近过程机械臂的规划曲线提出了要求；其次插孔过程中两轴孔的位置关系相互约束，限定了插孔过程中可调整的位姿幅度，对于单个轴孔插孔起效的位姿调整策略在双轴孔插孔控制中可能受到另一轴孔的约束而无法实现，要求阻抗控制下机械臂具有较小的刚性特性，同时设计参考轨迹时需要考虑进行多频次小幅度的往复位姿调整.

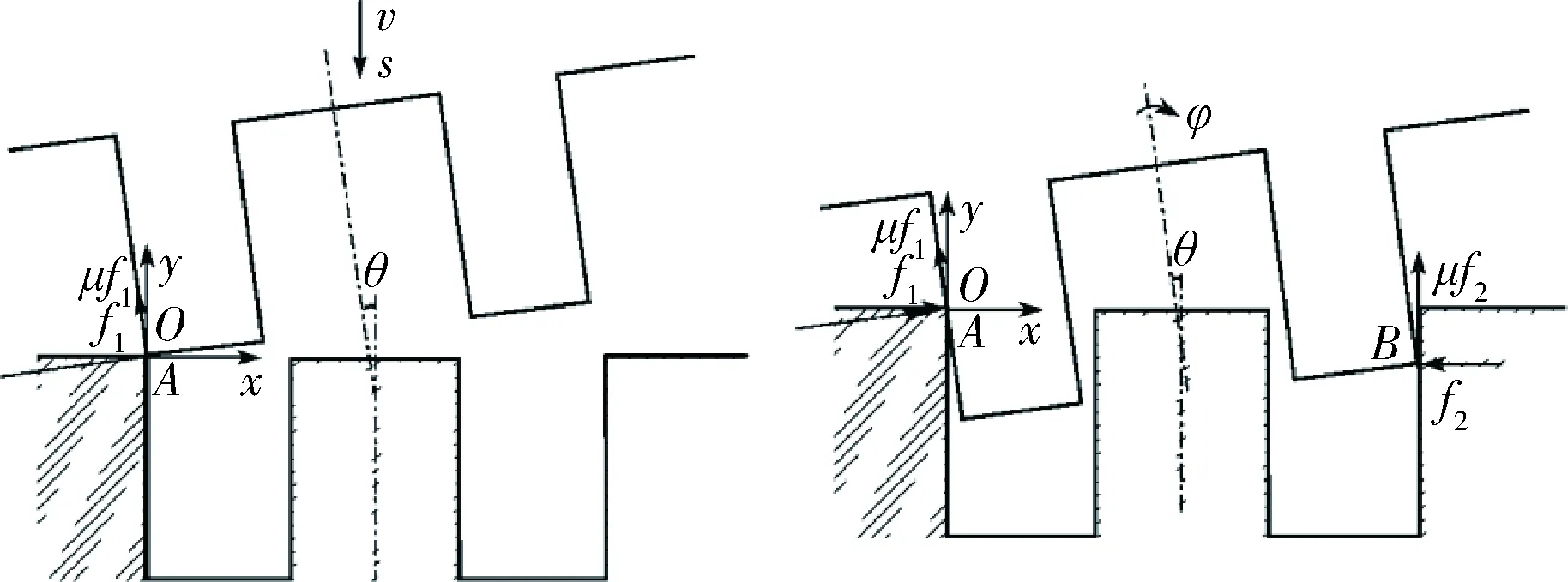
图3 双轴孔接触过程的受力Fig.3 The force on the contact process of the double axle hole

2 机械臂的运动学和动力学模型

本文以UR16e机械臂为操作对象，在不考虑机械臂和关节的被动柔顺特性的前提下，将机械臂连杆视为刚性细杆，连杆之间以单自由度旋转关节连接，机械臂特性如图4所示[12-13].

图4 UR16e机械臂的结构及参数Fig.4 Structure and parameters of UR16e robotic arm

根据UR16e工业机器人模型和尺寸，以各关节转动量为0的初始状态建立坐标系组，建立如表1所示的机械臂连杆D-H参数表.其中扭转角(αi)为第i个关节的坐标系Zi轴变换至与第i+1个关节的坐标系Zi+1轴方向重合过程中沿第i个关节的轴Xi旋转的角度，连杆长度(βi)为第i个关节的坐标系Zi轴与第i+1个关节的坐标系Zi+1轴沿第i个关节的轴Xi方向偏移的距离，关节偏距(di)为第i个关节的轴Xi与第i+1个关节的轴Xi+1沿第i+1个关节的坐标系Zi+1轴方向偏移的距离，关节转角(θi)为第i个关节的轴Xi变换至与第i+1个关节的轴Xi+1方向重合过程中沿第i+1个关节的坐标系Zi+1轴旋转的角度.

表1 UR16e机械臂D-H参数表Tab.1 UR16e robot arm D-H parameter table

使用拉格朗日动力学方法可以描述机械臂的动力学动态变化特性[14-15]：

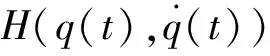
根据机械臂拉格朗日动力方程可根据给定的控制力矩可积分求解关节角度，在由运动学位姿坐标变换矩阵描述机械臂末端运动轨迹[16]；反之在通过轨迹规划设计机械臂运动的时间函数后可通过运动学反解求解关节变量，进而带入拉格朗日动力方程构成力矩控制系统.

3 机械臂双轴孔插孔的阻抗控制器设计

阻抗控制算法是解决机械臂与环境柔性交互的控制方法，当机械臂与外界环境产生接触力时机械臂会产生响应，将机械臂系统看作一个等效阻抗模型，系统的输入项与输出项测量值的比值即为系统的阻抗[17-18].将末端执行器位置变化与力变换之间的关系视为设计阻抗值，即可得到位置变化时外界环境作用于机械臂的力与机械臂末端位置关系的函数：

式中,M、B、K为期望阻抗参数，其中K为刚度系数矩阵，B为阻尼系数矩阵，M为惯性系数矩阵；Fext为机械臂受到外界环境的作用力，Fd为机械臂期望受到外界环境的作用力；xd为机械臂期望位置，x为机械臂实际位置.

阻抗控制的过程如图5所示，通过传感器检测机械臂受到的外力Fext得到与期望的偏差值，代入阻抗控制率将期望力偏差值转化为位置偏差值ex，进而得到机械臂的期望位置.将期望位置作为控制器的控制目标，控制机械臂运动的结果经传感器检测，实际的关节转角和实际接触力反馈分别用来修正目标期望和修正力矩,实现机械臂位置跟踪.

图5 阻抗控制框图Fig.5 Impedance control block diagram

在该控制系统中，设计阻抗控制器的期望阻抗参数M、D、K，使机械臂末端执行器具有“质量—弹簧—阻尼”的等价动力学性能，当机械臂末端执行器接触到环境障碍物时，机械臂受到环境力的作用不会发生刚性碰撞，减少其可能造成的部件损害和航天器姿态扰动，通过调整期望阻抗参数M、D、K可以调整机械臂阻抗控制的相应速度、稳定性和柔顺特性[19-20].

4 仿真结果分析

为验证这一阻抗控制算法解决双轴孔插孔问题的有效性，采用图1所示的六自由度串联型机械臂UR16e参数进行插孔的模拟仿真.

通过在Simulink和Vrep中建立联合仿真环境，在Simulink中建立阻抗控制器模型，将控制指令通过通信传输至Vrep中建立的UR16e机械臂模型中，模拟机械臂的运动轨迹及与环境力学交互特性，将模拟的输出通过虚拟力传感器采集传输反馈至Simulink的控制器中.

仿真过程中，设计机械臂末端工具在碰撞前保持不动，使用阻抗控制算法和传统刚性机械臂位置控制多次重复插孔过程，记录比较两种控制算法下插孔过程中的接触力和关节角变化趋势，实现本文提出的阻抗控制算法控制性能的验证.

采用两种控制算法的双轴孔插孔仿真结果如图6～8所示.两种控制算法控制下，机械臂于24 s后实现机械臂末端与目标问题的接触.在插孔过程中，采用阻抗控制算法控制下各轴方向接触力均在正负30 N的区间范围内波动；传统刚性机械臂位置控制算法控制下各轴方向力最大值均超过200 N，Z轴方向最大接触力可达500 N以上.采用阻抗控制方案能够在一定程度上降低碰撞交互瞬间的冲击力，降低机械臂和操作对象的发生碰撞破坏或运动姿态变化的不利影响.

图6 两种控制方法下X轴向接触力变化曲线Fig.6 Change curves of X-axis contact force under two control methods

图7 两种控制方法下Y轴向接触力变化曲线Fig.7 Change curves of Y-axis contact force under two control methods

图8 两种控制方法下Z轴向接触力变化曲线Fig.8 Change curves of Z-axis contact force under two control methods

对比两种控制算法下各轴方向接触力大小关系可以得出，阻抗控制算法将机械臂末端X轴向接触力减小至刚性机械臂位置控制算法的10%左右，Y轴向接触力减小至刚性机械臂位置控制算法的25%左右，Z轴向接触力减小至刚性机械臂位置控制算法的30%左右.总体而言阻抗控制算法显著降低了机械臂末端与环境的接触力，实现二者之间的柔顺交互.

采用两种控制算法的双轴孔插孔仿真过程中关节角位置变化过程部分曲线如图9和图10所示.采用阻抗控制算法控制下关节角位置变化更为平滑，几乎没有出现传统刚性机械臂位置控制算法控制下关节角位置突然变化的现象，可以有效减免机械臂运行过程中的冲击震荡.

图9 两种控制方法下关节角位置变化曲线Fig.9 Change curves of joint angle position under two control methods

图10 关节角位置变化曲线放大对比图Fig.10 Enlarged comparison of joint angle position curve

通过对阻抗控制算法和传统刚性机械臂位置控制算法的对比验证，这种基于阻抗柔顺控制的机械臂双轴孔插孔的柔顺控制方法对UR16e机械臂末端执行器的动力学性能起了良好的优化效果，对插孔过程的控制接触力产生了至少30%的削弱效果，稳定消除了控制过程的位置突变信号，使机械臂具有更平稳的控制过程和更柔顺的环境交互性能，最终可以实现良好的双轴孔插孔控制效果.

5 结 论

本文提出了一种基于阻抗柔顺控制的机械臂双轴孔插孔的柔顺控制方法，通过设计阻抗控制器的期望阻抗参数M、D、K，使机械臂末端执行器具有“质量—弹簧—阻尼”的等价动力学性能，减少其可能发生刚性碰撞造成的部件损害和航天器姿态扰动.在Simulink和Vrep中联合仿真环境中进行了控制器的模拟验证，最终实现了良好的柔顺双轴孔插孔效果.和传统控制原理的控制方案相比，本文提出的方法能有效实现双轴孔的柔顺插孔过程，具有更平稳的控制过程以及更微小的控制接触力，适应于在轨加注、在轨装配等需要同时实现双轴孔配合的空间操作需求.