基于参数反演的经高聚物注浆修复脱空后隧道二次衬砌的地震反应分析*

缪锋阳 黄正轩 徐建国 张金鹏 蔡迎春 耿玉鹏 张木天

(1.郑州大学水利科学与工程学院， 郑州 450001； 2.河南濮泽高速公路有限公司， 郑州 450000；3.伦敦国王学院，伦敦，WC2R2LS)

目前，我国隧道工程蓬勃发展，但衬砌背后脱空情况普遍存在于隧道中，已经成为隧道病害的主要诱因，其会导致隧道衬砌结构破坏、脱落、渗水等病害，对隧道的正常使用和运营安全造成了严重的影响[1-4]。造成隧道衬砌背后脱空的主要原因有：衬砌喷射混凝土厚度不足，围岩岩性变化大，防水板施工质量不达标，二次衬砌混凝土质量未达标，现场施工不合理等[2-8]。针对隧道衬砌脱空现象，应完善现有隧道衬砌的施工工艺，从施工工艺上杜绝脱空现象产生[8]，常采用拆除重建法、回填注浆法、喷射压注混凝土结合钢拱架加固方法修复填充脱空区[9-10]。但由于混凝土固有的缺陷，限制了隧道病害治理效果，鉴于高聚物材料早强、轻质、耐久好等优点[11-13]，很多学者将高聚物注浆技术应用到隧道工程中，目前涉及此方面的研究主要集中在高聚物注浆材料性能的研究[14-15]，快速治理隧道中的衬砌和路面缺陷、渗漏水等隧道病害[16-18]。结合高聚物注浆修复技术与隧道无损检测可以快速检测和修复隧道隐患[15,18]。高聚物注浆材料能够充分密实填充病害区，控制不利变形，较好地恢复结构的完整性[19-20]。在隧道地震响应方面，众多学者发现衬砌背后脱空区严重削弱了隧道的抗震性能，在地震作用下，脱空区衬砌产生了拉应力，脱空区周边围岩塑性变形严重，导致岩石掉落冲击衬砌，衬砌破坏坍塌严重[21-25]。现有文献鲜有关于高聚物注浆修复后隧道地震响应的研究。因此，依托龙眠山隧道工程，应用系统识别灵敏度分析方法反演隧道围岩力学参数，并借助数值模拟软件改进反演方法，利用改进后的反演结果优化隧道动力响应数值模型，进而研究在地震荷载作用下，龙眠山隧道采用高聚物注浆修复衬砌背后脱空区后的修复效果和抗震能力，为隧道脱空高聚物注浆修复提供参考。

1 工程概况

龙眠山隧道位于六安市舒城县汤池镇与桐城市大关镇交界处，为分离式隧道，埋深在50～300 m，起始桩号为K81+834(ZK81+830)，终止桩号为K84+47(ZK84+450)，全长2 644 m(2 620 m)。隧道所处的围岩等级主要是Ⅲ、Ⅳ、Ⅴ级围岩，其中Ⅲ、Ⅳ级围岩主要为中风化花岗岩、Ⅴ级围岩主要为全风化花岗岩。

龙眠山隧道的量测项目包括：地表下沉、拱顶下沉、周边收敛等。由龙眠山隧道右线K83+020断面拱顶沉降(图1)可以看出：在第40天以后围岩基本达到稳定状态，累计沉降值保持在10 mm以下，拱顶沉降曲线发展趋势近似呈对数函数曲线，沉降最终保持在9.4 mm。拱顶沉降速率在整体上也是呈缓慢下降状(图2)，在第40天以后，沉降速率保持相对稳定，在0.1～0 mm/d。最大沉降速率为第5天，达到0.6 mm/d，出现在开挖下台阶的时候，由于最大变化速率的持续时间比较短，不会对隧道开挖过程中的整体稳定性和安全性造成太大的影响。总体而言，该断面的拱顶变形在各阶段都处于合理范围，未见异常，围岩基本稳定，开挖方式合理。

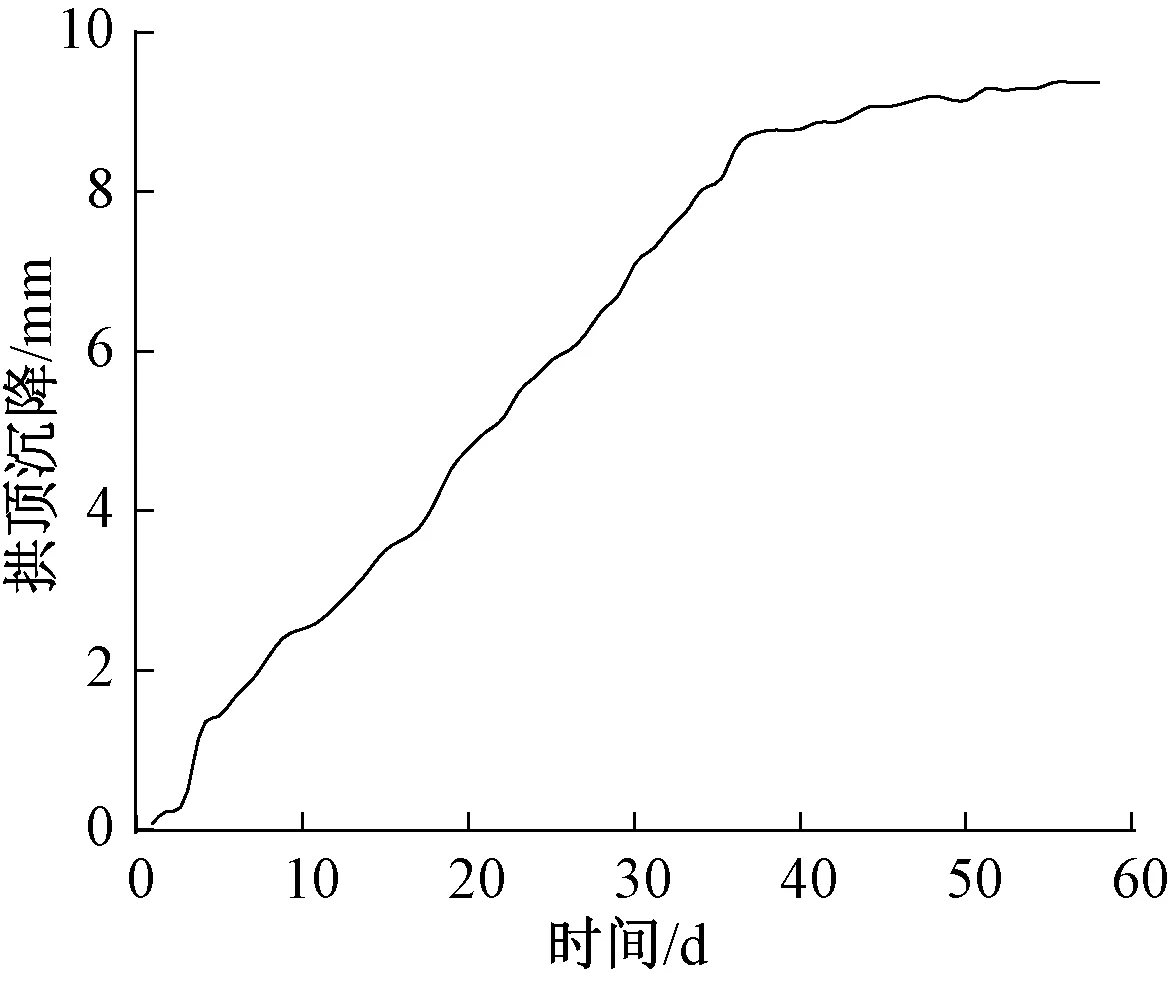
图1 K83+020断面拱顶沉降Fig.1 The settlement of the vault in section K83+020

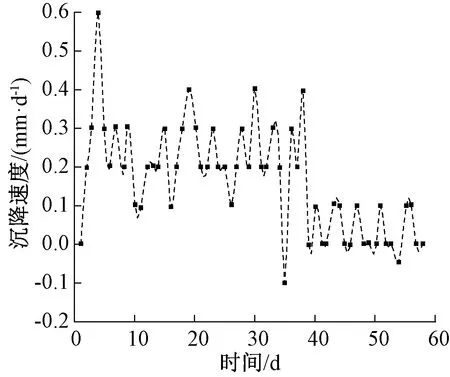
图2 K83+020断面拱顶沉降速率Fig.2 The settlement rate of the vault in section K83+020

对龙眠山隧道右线K83+020断面周边收敛变形数据(图3)分析发现，该断面的累计周边收敛值要小于拱顶沉降值，其变形过程中的规律性较拱顶变形散乱，其结果仍然趋向于收敛状态。整个收敛变形过程中，收敛速率(图4)在前期较大，峰值达到0.4 mm/d，持续时间仍较短，而后急剧下降，收敛速率稳定在0.3～0.1 mm/d，在第25天出现收敛变形负增长的现象，在此过程中洞身并没有出现明显的破坏迹象。第40天以后，洞身收敛值保持在7 mm左右；达到7.3 mm时，收敛速率稳定在0.1 mm/d以内，可判定基本收敛，洞身稳定，无异常情况。

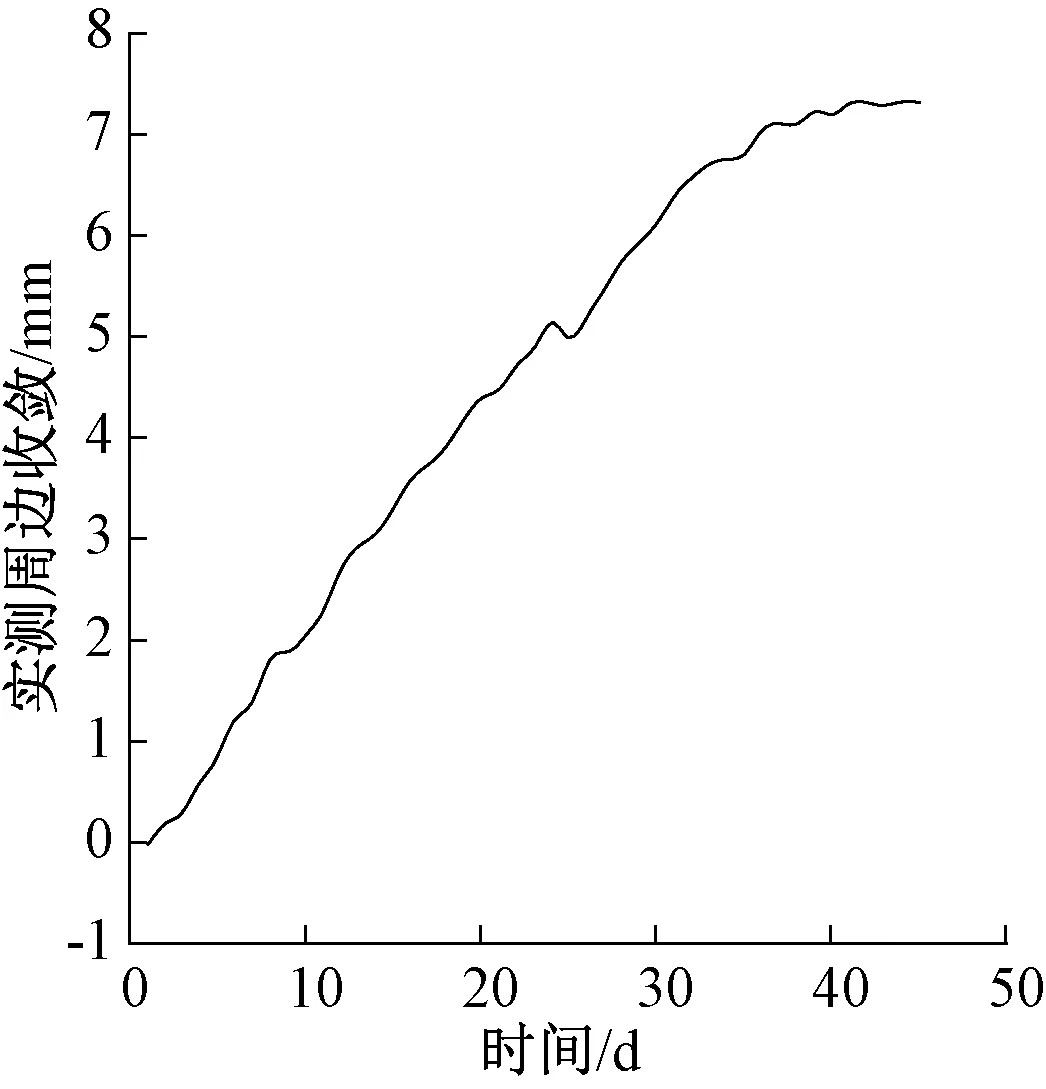
图3 K83+020断面周边收敛曲线Fig.3 The peripheral convergence curve of section K83+020

图4 K83+020断面周边收敛速率曲线Fig.4 The peripheral convergence rate curve of section K83+020

2 隧道开挖数值模拟

2.1 隧道开挖过程模拟

数值模拟对象为龙眠山隧道右线K83+010～K83+90路段，开挖长度为80 m，隧道埋深约为100～110 m，地势较为平缓，该路段为Ⅳ级围岩，岩层类型为中风化花岗岩，采用上、下台阶法掘进。模型左、右边界取隧道洞径的3倍，宽度为100 m；下边界为洞径的3.5倍，选取高度为150～160 m；隧道距土体底部高度为50 m，埋深为100～110 m。结合隧道地勘报告，土体模型采用弹塑性模型中的Mohr-Coulomb模型，土体密度取1.8 g/cm3，变形模量为2.6 GPa，泊松比为0.32，摩擦角为34°，黏聚力为0.5 MPa。隧道的超前支护结构为φ25超前中空注浆锚杆，密度为7.8 g/cm3，弹性模量为200 GPa，泊松比为0.2。衬砌采用C25素防水混凝土，密度为2.4 g/cm3，弹性模量为20 GPa，泊松比为0.2。仰拱与二衬采用模筑C30混凝土，密度为2.5 g/cm3，弹性模量为25 GPa，泊松比为0.2。衬砌与围岩通过Tie约束绑定在一起，在隧道模型的前、后、左、右边界均施加了法向约束，底部边界为全约束，上边界为自由边界，重力荷载作用在整个模型上。对隧道模型整体划分网格，土体整体布设较疏，隧道部分边界布设较密，采用中性轴算法，锚杆的单元类型为桁架单元，网格单元总数为126 600个，划分好网格的隧道模型如图5所示。

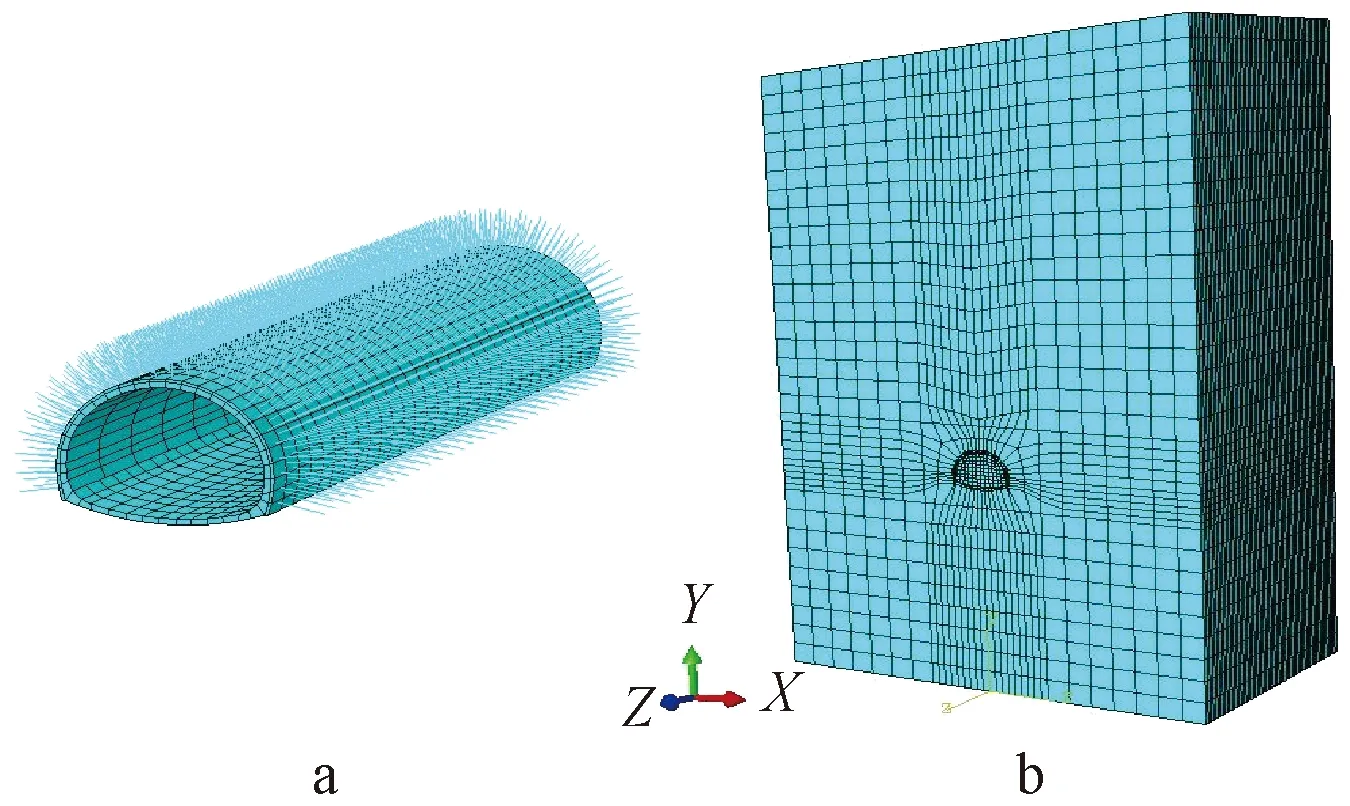
图5 隧道模型Fig.5 The numerical simulation model of the tunnel

2.2 结果分析

通过图6的位移云可知：拱顶是初支结构的最大竖向位移处，达到 6.267 mm。拱腰部位出现最大的横向位移，达到2.456 mm。而目标断面实测拱顶沉降值以及周边收敛值分别为9.4，7.3 mm，其差值较大，累计拱顶沉降值相差3.133 mm，累计收敛值相差2.31 mm。为了更好地验证数值模型的准确性，提取衬砌1点处的竖向位移，以及2、3两点的横向位移的求和(取点位置如图7所示)，绘制成曲线，并分析对比该衬砌所在断面的实测拱顶下沉值与周边收敛值变形趋势。

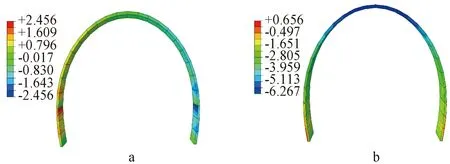
a—横向位移云； b—竖向位移云。图6 龙眠山隧道右线K83+020断面初衬横向位移云和竖向位移云 mmFig.6 The contours for transverse and longitudinal displacement of the initial lining in the section K83+020 of the right line in the Longmianshan tunnel

图7 数值模型中目标断面初衬监测点示意Fig.7 The monitored points in the target section of the primary lining in the numerical model

由图8 K83+020断面拱顶实测沉降值和周边收敛值与模型计算值的对比可以发现：由于选取土体力学参数与真实围岩力学参数的差异性，所得到的分析结果与真实情况也存在差异，但是数值模拟的初衬位移变化情况与隧道真实开挖的变形规律相符合，说明对龙眠山隧道开挖过程的数值模拟符合真实的开挖工序，其应力-应变的差异性是由于模拟过程隧道围岩的力学参数设置不偏差造成的，可以通过围岩力学参数的反演分析，得到贴近较真实的围岩力学参数。

a—拱顶沉降实测值(点1)与模拟值对比； b—周边收敛实测值(点2)与模拟值对比。-----模拟曲线； ——实测实线。图8 K83+020断面拱顶沉降实测值或周边收敛实测值与模拟值对比Fig.8 Comparisons between the measured and simulated values of the vault settlement or peripheral convergence in section K83+020

3 隧道围岩力学参数反演分析

3.1 围岩三维力学参数反演分析

已有学者将系统识别灵敏度分析方法应用在层状路面结构反算、路面结构层材料介电特性及其厚度的反演、隧道围岩参数反演分析中[26-31]，但是目前系统识别灵敏度分析方法主要应用于隧道围岩二维参数的反演，且在反演分析中使用的隧道监测数据较少，如文献[28-29]介绍了根据隧道断面的实测水平收敛值、拱顶下沉值对隧道围岩的弹性模量、泊松比进行的反演分析。基于龙眠山隧道所建立的正演模型为三维Mohr-Coulomb模型，在隧道围岩三维参数反演分析领域中引入系统识别方法，如图9所示，根据实测某隧道断面的周边收敛值s′1、拱顶沉降值s′2、实测断面的拱顶沉降值s′3，反演计算围岩的静弹性模量、泊松比和内摩擦角三个参数，能够实现模型参数调整过程的高精度化和高效自动化，基本过程如下：

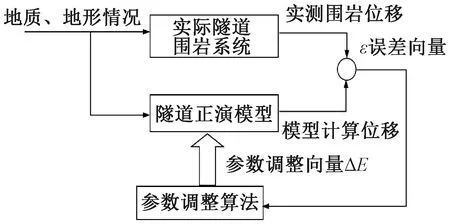
图9 隧道围岩参数反算系统识别基本过程Fig.9 The basic process for identification parameters of surrounding rock in the inverse calculation system

1)设置初始围岩力学参数。首先假设初始的内摩擦角φ0、弹性模量E0、初始泊松比μ0，将E0、μ0以及φ0输入到有限元正演模型计算与实测值对应断面的位移值：

{s}={s1,s2,s3}T

(1)

2)将计算值{s}与实测值{s′}相比较。若计算值与实测值之差的绝对值很小，即计算结果满足要求，取max{{Δs}T{Δs}}≤ε(ε为计算精度)，立即终止反演分析计算，此时模型的弹性模量、泊松比及内摩擦角即为实际围岩材料的弹性模量、泊松比及内摩擦角。如果max{{Δs}T{Δs}}>ε，则应该调整围岩的弹性模量、泊松比及内摩擦角。

3)建立灵敏度矩阵。利用前向差分法建立灵敏度矩阵，求出初始弹性模量E0、初始泊松比μ0、初始内摩擦角φ0下的计算值{s(E0,μ0,φ0)}；然后求出在弹性模量为E0+ΔE时，泊松比为μ0、内摩擦角为φ0的{s(E0+ΔE,μ0,φ0)}；再求出在弹性模量为E0、内摩擦角φ0不变，泊松比为μ0+Δμ时的{s(E0,μ0+Δμ,φ0)}；再求出弹性模量E0、泊松比μ0不变，内摩擦角为φ0+Δφ时的{s(E0,μ0,φ0+Δφ)}，取ΔE=1%E，ΔE=Δμ=1%μ，Δφ=1%φ，从而得：

(2)

{Δs}=[D]{Δx}

(3)

将实测值与初始弹性模量E0、初始泊松比μ0、初始内摩擦角φ0下的计算值的差{Δs}和灵敏度矩阵D输入到编制好的数值分析程序，程序会计算出参数调整向量{Δx}。

5)进行第一次迭代。令

(4)

求出弹性模量E1、泊松比μ1、内摩擦角φ1下的计算值{s}(1)={s(E1,μ1,φ1)}(1)，上标“(1)”代表第一次参数调整，然后回到第2步，直到满足要求为止。

3.2 龙眠山隧道围岩力学参数反演

经过多次参数调整，假设围岩初始力学性能参数E0=2.0 GPa、μ0=0.32、φ0=32°，根据提出的围岩三维力学参数反演方法进行反演计算，进行四次迭代得到E=1.82 GPa、μ=0.32、φ=35°，此时隧道有限元模型计算得到的周边收敛值s1=7.255 4 mm，拱顶沉降值s2=9.531 7 mm，拱顶沉降值s3=8.820 6 mm。由于实测s′1=7.322 4 mm、s′2=9.466 9 mm、s′3=8.712 8 mm，可见，模拟值与实测值已十分接近，根据模型结果对于隧道的实测结果可得到表1。

表1 隧道断面位移变化对比Table 1 Comparisons of displacement in the tunnel sections mm

此时{Δs}T{Δs}=0.046 6 mm，满足条件max{{Δs}T{Δs}}≤1.0×10-5m，可知龙眠山隧道数值模拟的Ⅳ级围岩路段真实围岩力学参数为弹性模量为1.82 GPa，泊松比为0.32，内摩擦角为35°。依据系统识别灵敏度分析方法进行反演得到最终围岩参数建立正演模型，提取其隧道右线K83+020断面的位移变化模拟值与实测绘制拟合曲线如图10所示。

a—断面周边收敛对比； b—拱顶沉降对比。—实测； -----模拟。图10 隧道目标断面(K83+020)拱顶沉降模拟值与实测值对比Fig.10 Comparisons of settlement values between the simulated and measured values of vaults in the target section (K83+020) of the tunnel

对比目标断面模拟值与实测值位移变化拟合曲线可知，应用系统识别灵敏度分析方法对隧道围岩力学参数进行位移量测反演分析后得到的力学参数再代入数值模型中进行正演，在隧道施工的各个阶段，数值模型中各目标断面的拱顶变形量和周边收敛量与实际监控量测结果误差值均较小，误差范围在0.3 mm以内。目标断面在开挖过程的位移云(图6)结果也符合实际的上、下台阶施工过程中的位移分布规律。

4 隧道脱空高聚物注浆修复地震响应分析

4.1 隧道脱空检查和修复

在龙眠山隧道右线K83+140～K83+350路段采用地质雷达法进行衬砌施工质量检测，发现在隧道顶部的衬砌与岩体之间有一个最大深度达20 cm、纵长约2～3 m的脱空区，如图11所示。

根据雷达提供的数据，对脱空区进行注浆修复，与混凝土注浆材料相比，高聚物注浆材料抗渗性能、抗压性能、抗拉性能优秀，耐腐蚀能力强，高聚物修复材料反应后，不仅能够迅速发生体积膨胀(体积膨胀10～20倍)，自动密实加固脱空区，对结构病害区进行再压实加固，而且质量轻，施工效率高，时间成本低，经济性高，注射高聚物材料后15 min内，高聚物材料即可达到90%的足够强度[11-13]，故所用注浆材料为非水反应类高聚物。通过对比高聚物注浆前、后雷达探测频谱图(图12)发现，衬砌背后脱空区注浆效果良好，衬砌结构的完整性和密实性明显提高，为了更好地验证高聚物材料对于隧道脱空修复效果，开展了在地震作用下隧道高聚物注浆修复前后的地震响应对比分析。

a—高聚物注浆前; b—高聚物注浆后。图12 注浆前、后地质雷达探测频谱Fig.12 Geological radar detection spectrums before and after grouting

4.2 数值模型创建

依据龙眠山隧道K83+140～K83+350路段围岩等级和隧道埋深建立数值模型，隧道埋深为70 m，开挖深度160 m，隧道脱空区位于隧道开挖深度80～83 m处。通过围岩三维力学参数反演方法计算出隧道围岩的静弹性模量为1.82 GPa，泊松比为0.32，内摩擦角为35°，根据文献[32]，考虑到静弹性模量与动弹性模量的之间的关系，由此隧道岩土体的围岩动弹性模量为18.63 GPa。注浆所用的高聚物材料为非水反应类高聚物材料，密度为1.6 g/cm3，弹性模量为20.2 MPa，泊松比为0.3。划分好网格的模型如图13所示。进行地震分析时选取的三条天然地震波分别为：Northridge波(Ⅰ类场地)、Taft波(Ⅱ类场地)、El Centro波(Ⅲ类场地)，对应加速度峰值为0.1g，时间间隔为0.02 s，有效历时为19.2 s。

图13 脱空区域示意Fig.13 The schematic diagram of the void zone

4.3 隧道地震力学响应及注浆修复情况分析

4.3.1地震荷载作用位移分析

由于脱空区域位于隧道顶部，二次衬砌顶部节点竖向位移和竖向加速度的对比可以直观地反映高聚物注浆对于脱空区的影响。由图14～16可以看出:在整个时间历程震动过程中，二次衬砌顶部在正常情况下的竖向位移和竖向加速度均最小，在顶部脱空时竖向位移和竖向加速度最大，对脱空区进行注浆修复后得到明显改善。在Northridge波作用下，正常情况工况、顶部脱空工况、脱空修复后工况的竖向最大位移分别为5.33，6.15，5.68 mm，竖向最大加速度分别为1.32，1.56，1.43 m/s2，与正常情况相比，顶部脱空时二次衬砌顶部竖向最大位移和竖向最大加速度的增幅为15.4%和18.5%，注浆修复后，竖向最大位移和竖向最大加速度的增幅为6.6%和8.3%，较顶部脱空时增幅减小了7.6%和8.3%。在Taft波作用下，正常情况工况、顶部脱空工况、脱空修复后工况的竖向位移分别为3.78，4.07，3.95 mm，竖向加速度分别为1.08，1.17，1.12 m/s2，与正常情况相比，顶部脱空时二次衬砌顶部竖向位移和竖向加速度的增幅为7.7%和8.3%，注浆修复后，竖向位移和竖向加速度的增幅为4.5%和3.7%，较顶部脱空时增幅减小了2.9%和4.3%。在El Centro波作用下，正常情况工况、顶部脱空工况、脱空修复后工况的竖向位移分别为2.97，3.85，3.44 mm，竖向加速度最大值分别为0.91，1.04，0.97 m/s2，与正常情况相比，顶部脱空时二次衬砌顶部竖向位移和竖向加速度的增幅为29.6%和14.3%，注浆修复后，竖向位移和竖向加速度较正常情况的增幅为15.8%和6.6%，较顶部脱空时增幅减小了10.6%和6.7%。可见，高聚物注浆对于脱空区的修复效果显著，使得支护结构在地震荷载作用下位移减小，更加的稳定。

a—竖向位移； b—竖向加速度。正常情况； 顶部脱空； 注浆修复。图14 隧道在Northridge波作用下不同工况的二次衬砌顶部竖向位移及加速度时程曲线Fig.14 Time-history curves of vertical displacement and acceleration at the top of the secondary lining in the tunnel in different working conditions excited by Northridge Wave

a—竖向位移； b—竖向加速度。正常情况； 顶部脱空； 注浆修复。图15 隧道在Taft波作用下不同工况的二次衬砌顶部竖向位移及加速度时程曲线Fig.15 Time-history curves of vertical displacement and acceleration at the top of the secondary lining in the tunnel in different working conditions excited by Taft Wave

a—竖向位移； b—竖向加速度。正常情况； 顶部脱空； 注浆修复。图16 隧道在El Centro波作用下不同工况的二次衬砌顶部竖向位移及加速度时程曲线Fig.16 Time-history curves of vertical displacement and acceleration at the top of the secondary lining in the tunnel in different working conditions excited by El Centro Wave

在不同场地条件同一峰值的地震波作用下，二次衬砌顶部的竖向加速度和竖向位移均存在明显的差异，Northridge波(Ⅰ类场地)激励下竖向位移和竖向加速度最大，El Centro波(Ⅲ类场地)激励下竖向位移和竖向加速度最小，即随着场地类型从坚硬、中硬到中软，对二次衬砌顶部的位移及加速度响应影响逐渐减小，说明该隧道模型的动力响应具有明显的地震波频谱敏感性。

4.3.2地震荷载作用应力分析

由图17～19可以看出:在三种竖向地震荷载作用下，不同工况隧道支护结构整体都表现为受压状态。在Northridge波作用下，二次衬砌顶部在正常情况工况、顶部脱空工况、注浆修复后工况的最大主应力绝对值的最大值分别为0.211,0.260,0.241 MPa，最小主应力绝对值的最大值为7.49,8.85,8.15 MPa。与正常情况相比，顶部脱空时二次衬砌顶部最大主应力绝对值的最大值和最小主应力绝对值的最大值的增幅为23.2%和18.2%；注浆修复后，最大主应力绝对值的最大值和最小主应力绝对值的最大值较正常情况的增幅分别为14.2%和8.8%，较顶部脱空时增幅减小了7.3%和7.9%。在Taft波作用下，二次衬砌顶部在正常情况工况、顶部脱空工况、注浆修复后工况的最大主应力绝对值的最大值分别为0.196,0.241,0.218 MPa，最小主应力绝对值的最大值为6.90,7.95,7.21 MPa，与正常情况相比，顶部脱空时二次衬砌顶部最大主应力绝对值的最大值和最小主应力绝对值的最大值的增幅为23.0%和15.2%；注浆修复后，最大主应力绝对值的最大值和最小主应力绝对值的最大值较正常情况的增幅为11.2%和4.5%，较顶部脱空时增幅减小了8.3%和9.5%。在El Centro波作用下最大主应力绝对值的最大值分别为0.187,0.233,0.208 MPa，二次衬砌顶部在正常情况工况、顶部脱空工况、注浆修复后工况的最小主应力绝对值的最大值为6.57,7.55,6.95 MPa，与正常情况相比，顶部脱空时二次衬砌顶部最大主应力绝对值的最大值和最小主应力绝对值的最大值的增幅为24.6%和14.9%；注浆修复后，最大主应力绝对值的最大值和最小主应力绝对值的最大值较正常情况的增幅为11.2%和5.8%，较顶部脱空时增幅减小了10.7%和7.9%。可见，相比顶部脱空工况，注浆修复后的二次衬砌顶部压应力明显偏小，接近于正常情况，达到了预期修复效果，使得支护结构的整体受力变形更趋于安全稳定。

a—最大主应力； b—最小主应力。图17 隧道在Northridge波作用下不同工况的二次衬砌顶部应力变化曲线Fig.17 Time-history curves of stress at the top of the secondary lining in the tunnel in different working conditions excited by Northridge Waves

a—最大主应力； b—最小主应力。正常情况； 顶部脱空； 注浆修复。图18 隧道在Taft波作用下不同工况的二次衬砌顶部应力变化曲线Fig.18 Time-history curves of stress at the top of the secondary lining in the tunnel in different working conditions excited by Taft Wave

在不同场地条件同一峰值的地震波作用下，二次衬砌顶部最大主应力绝对值的最大值、最小主应力绝对值的最大值存在明显的差异，Northridge波(Ⅰ类场地)激励下最大主应力绝对值的最大值、最小主应力绝对值的最大值最大；El Centro波(Ⅲ类场地)激励下竖向最大主应力绝对值的最大值、最小主应力绝对值的最大值最小；即随着场地类型从坚硬、中硬到中软，对二次衬砌顶部的应力作用影响逐渐减弱，说明该隧道模型的动力响应具有明显的地震波频谱敏感。

5 结束语

以在建的龙眠山隧道作为工程背景，对其施工过程进行了数值模拟，利用系统识别灵敏度分析方法对Ⅳ级围岩路段进行隧道围岩力学物理参数反演，最后对高聚物注浆修复脱空隧道的地震动力响应进行了分析，得到以下结论：

1)利用有限元软件对龙眠山隧道工程进行数值模拟，发现隧道围岩和支护结构的变形规律和应力分布规律符合现场施工情况，但拱顶沉降、周边收敛等变形量与实际监控量测数据有差异，这种差异是由数值模型选取的围岩力学参数与实际不符造成的差异主要原因是数值模型选取的围岩力学参数与实际不符造成的，故此提出利用监控量测数据以及数值模型，对隧道围岩力学参数进行反演分析。

2)基于系统识别灵敏度分析方法，对二维参数反演方法进行改进，开展围岩三维物理力学参数反演分析公式的推导，并对龙眠山隧道右线K83+010～K83+90路段围岩进行三维力学参数反演分析，得到最终符合实际的围岩力学参量, 证明了系统识别灵敏度分析方法的可行性，对在建龙眠山隧道工程的实时检测具有重要的参考价值，并为准确建立隧道及围岩整体结构有限元模型并开展动力响应分析提供了保障。

3)通过地震力学响应分析验证了高聚物注浆修复隧道脱空效果显著。隧道二次衬砌顶部脱空区域在注浆修复后，位移和应力明显减小，接近于正常情况。但在不同场地条件同一峰值的地震波作用下，二次衬砌顶部的应力、位移均存在明显的差异，随着场地类型从坚硬、中硬到中软，对二次衬砌顶部的位移、应力响应影响逐渐减小，说明该隧道模型的动力响应具有明显的地震波频谱敏感性。