砂土垫层对管廊穿越活动地裂缝响应的影响分析*

徐 强 白超宇 李文阳 陈浩然 安 鹏 李良成

(1.长安大学地质工程与测绘学院， 西安 710054； 2.自然资源部地裂缝与地面沉降野外科学观测研究站， 西安 710054；3.机械工业勘察设计研究院有限公司， 西安 710043)

0 前 言

据统计，2019年10月—2020年9月，中国至少发生了1 008起地下管线相关事故，造成105人遇难，234人受伤。地下综合管廊是建设在城市地下用于集中布设电力、通信、广播电视、给水等市政管线的公共设施，它便于各类管线的抢修、维护、扩容改造等，可大大缩减管线的抢修时间。由于地下管线的破坏以及带来的次生灾害难防难治，所以，地下综合管廊的建设具有重要的意义[1-4]。

1833年法国巴黎就建成世界上第一条地下管线综合管廊，19世纪60年代末为适应现代城市管线种类多和敷设要求高的特点，法国将综合管廊的断面改成了矩形。目前对管廊的研究主要有管廊的力学特性和灾害响应等[5-11]。

西安地裂缝是西安城市主要的地质灾害之一[12-15]，自西安发现地裂缝以来，西安规划区已经基本查清14条活动地裂缝，每条地裂缝长度长达数公里到数十公里，总长已超过200 km，覆盖面积约250 km2[12]。地裂缝活动对线型工程的安全性具有极大的隐患[16-22]。

目前西安地裂缝的活动强度较20世纪70年代中期—20世纪90年代初期有所减缓，但由于各地裂缝活动周期性的差异所导致的活动速率的差异仍十分明显。根据对1996—2005年西安地裂缝年平均活动速率的调查，目前西安地裂缝最大平均活动速率达到了5 mm/a，管廊的设计使用年限为100 a，因此，地裂缝活动的长期累积错位必将对管廊的运维产生不利影响[12]。闫钰丰等研究了管廊采用柔性接头与地裂缝正交下的受力和变形特征[23]。胡志平等通过模型试验对管廊45°斜穿地裂缝时上、下盘相对错动对管廊的变形规律进行了研究[24]。王启耀等对双仓管廊70°大角度斜交地裂缝进行了数值研究，得出管廊同时具有纵向弯曲变形、横向剪切变形和扭转变形的结论[25]。徐强等分析了不同斜交角度对管廊穿越地裂缝的影响[26]。

已有研究多集中在地裂缝活动对管廊的内力和变形破坏特征分析，而管廊穿越活动地裂缝的防治措施较少。西安地裂缝分布范围几乎遍布城区，已有管廊规划与地裂缝分布图如图1所示[22]，可见地下综合管廊建设与运维不可避免受到地裂缝活动的影响。综合已有文献结论，地下综合管廊穿越地裂缝的破坏形态与受力特征多表现为：管廊在地裂缝活动作用下的破坏多为顶面混凝土受拉破坏，且最大拉应力出现在靠近地裂缝的下盘一侧。分析其原因应是上盘土体沉降，使得下盘靠近地裂缝处土体对管廊竖向接触力增大而表现出对管廊拱起的作用显著，最终使得该处管廊顶面受拉开裂。可见，若消减下盘对管廊拱起的作用，应能提高地下综合管廊穿越地裂缝的适应性。因此，基于砂土的流动特性，提出将与管廊底面接触的一部分土体换填为砂土的防治措施，藉此分析换填砂土的范围对地下综合管廊穿越地裂缝的变形和内力响应影响。

图1 西安地下综合管廊规划与地裂缝分布Fig.1 The planning of underground utility tunnels and the distribution of ground fissures in Xi’an

1 地裂缝对管廊影响作用数值模型

1.1 模型试验地裂缝活动对矩形隧道影响分析

已有大型物理模型试验，对矩形截面隧道穿越地裂缝的变形和破坏进行了研究[13]，隧道模型长×宽×高尺寸为：10.0 m×1.2 m×1.3 m，隧道壁厚为120 mm，隧道采用明挖埋设，埋深为2.2 m，隧道穿越地裂缝模型如图2所示[13]。试验中隧道采用混凝土结构，混凝土强度等级为C25，土体抗剪强度指标：c为30 kPa、φ为10°，隧道位置和土层参数如图3所示[13]。

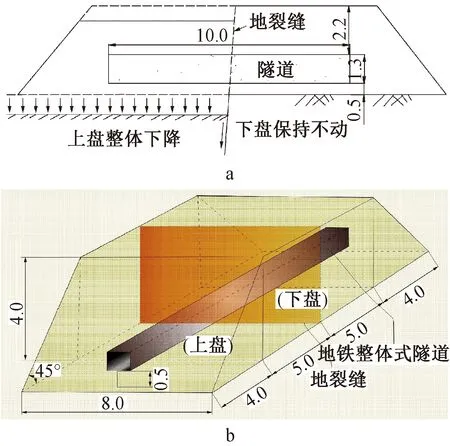
a—纵剖面； b—三维模型。图2 地裂缝与地铁隧道模型示意 mFig.2 The schematic diagram of the ground fissure and the subway tunnel model

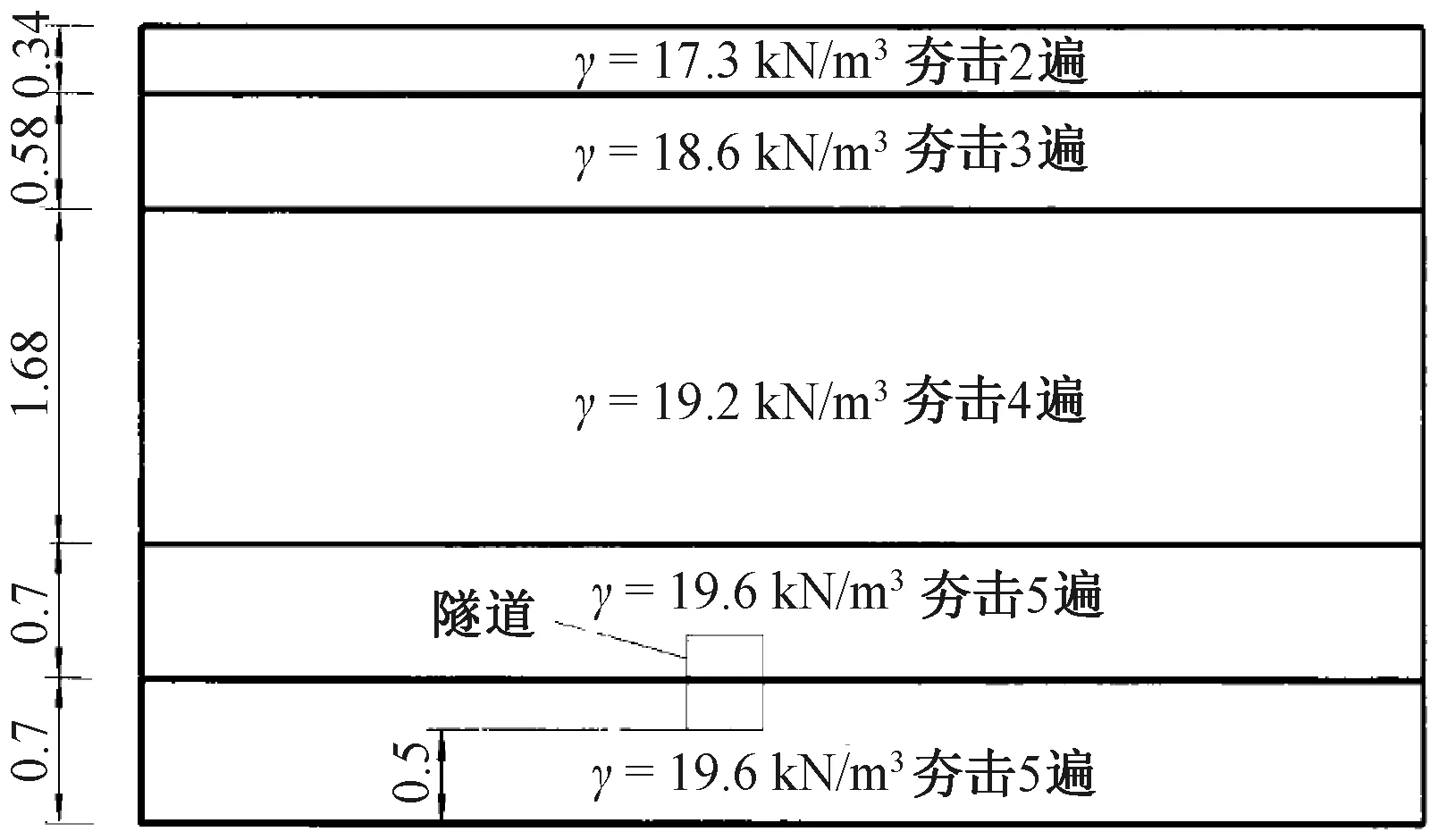
图3 隧道布置与土层参数示意 mFig.3 The schematic diagram of the tunnel layout and soil stratum parameters

上盘不同竖向沉降量下隧道顶面的纵向应变如图4所示[13]。可见，隧道顶面的应变变化大于底面，隧道纵向最大应变出现在隧道顶面下盘靠近地裂缝位置，且随着沉降位移的增加，纵向应变逐渐增大。其原因在于地裂缝的活动使得隧道上盘底部脱空，下盘底部的土体压力迅速增大，隧道在该处受到较大的向上反力。在下盘底部土反力与下盘上覆土压力共同作用下，隧道下盘上部受拉。此外，当沉降位移超过4 cm后，隧道的纵向应力随沉降位移的增加而增大的增幅不大，可知沉降位移达到或超过4 cm后，隧道在该处受拉开裂，由于物理模型试验中，隧道内配有钢筋，虽然钢筋对隧道混凝土开裂前的纵向刚度影响较小，但混凝土开裂后钢筋受力将明显增大，使得隧道应力重新分布，混凝土在裂缝两侧的应力稳定且平缓。

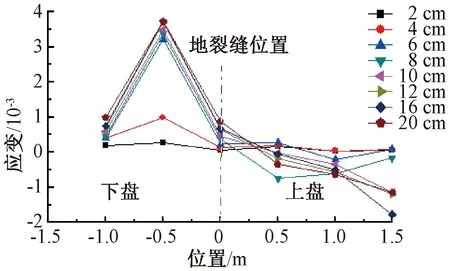
图4 隧道顶部混凝土应变纵向变化曲线Fig.4 Longitudinal strain curves of concrete at the top of the tunnel

1.2 物理模型试验结果的数值模型验证

物理模型试验中管廊两端土体主要起整体稳定作用，对管廊影响可忽略不计，分析采用ABAQUS建立数值模型，依据物理模型试验参数，建立其数值模型，如图5所示。为更加符合实际，减小两侧上覆土的影响，从管廊底部两侧斜向上沿土体内摩擦角设切向接触面，管廊与土体之间采用通用接触，切向摩擦系数设为0.3，为了使得管廊能与土体脱开，法向设为硬接触。

图5 物理模型试验的数值模型Fig.5 The numerical model of the physical model test

地裂缝倾角为80°，对比矩形隧道正交地裂缝下竖向沉降为20，40，60 mm时的纵向应力变化曲线(图6)可见：数值模型与物理模型试验结果的纵向应变规律相同，都表现出当地裂缝竖向沉降超过4 cm时，管廊下盘顶面混凝土超过其材料抗拉强度，发生受拉破坏。表明数值模型的有效性，能够反映矩形隧道受地裂缝活动影响作用。

1.3 实际工况下管廊穿越地裂缝的数值模型

由于选取模型试验为矩形断面，与管廊结构特征相似，受地裂缝影响规律接近，可作为管廊穿越活动地裂缝的试验数据，通过与实际模型试验结果对比，已验证数值模型有较高的准确性。

研究的目的是分析砂土换填前后以及不同换填范围(长度、坡角与厚度)工况下管廊的变形特征和受力性能。西安地裂缝的倾角大多在80°左右，地下综合管廊一般采用明挖施工，管廊顶部覆土厚度大多在4～10 m。目前西安地裂缝的活动量为1～5 mm/a，地下综合管廊的设计使用年限为100 a，若以最大活动速率5 mm/a来计算，地下综合管廊须能够适应500 mm的地裂缝竖向差异沉降量。研究成果显示：管廊整体穿越地裂缝时，可承受的最大地裂缝运动在100 mm左右，若采用管廊设缝处理，则接头处都为管廊薄弱区，较大的沉降差对防水和内部管线布置不利，且施工极为不方便。因此，尝试不设缝，采用地基砂土换填的方式，提高地下综合管廊穿越活动地裂缝的适应性，减轻地裂缝活动对地下综合管廊内力影响。地下综合管廊采用不设缝的方式整体穿越地裂缝，保持下盘不动，上盘沿地裂缝倾角斜向下沉降，地裂缝的竖向沉降差分别取50，100，150，200 mm。为充分研究地裂缝对地下综合管廊的受力和变形响应，同时减少两端边界设置对管廊的影响，管廊长度取120 m，地裂缝设置在管廊纵向中点处并与管廊正交，上、下盘各长60 m。徐强等分析显示，管廊与地裂缝交角越大，管廊拱起现象越明显[26]。因此，仅分析管廊与地裂缝正交，不考虑斜交情况。

管廊模型的横截面采用三仓形式，横截面宽度×高度尺寸为9 m×4 m，外壁厚为0.5 m，内壁厚为0.4 m，混凝土强度等级取C45，为消除边界影响，模型长×宽×高尺寸取120 m×40 m×40 m，混凝土材料本构关系采用弹性模型，土体采用摩尔-库仑模型。混凝土的弹性模量为33 500 MPa，混凝土的密度为2 500 kg/m3，泊松比为0.2。地裂缝的模拟采用在上、下盘之间设置接触对，采取硬接触的方式，以保证接触面在负压力下能够彼此脱开，常见的土体接触面摩擦系数范围值为0.15～0.70，计算中采用0.3。土层土性参数取西安实际地层参数以及换填砂土参数，如表1所示[26-27]。

表1 土层土性物理力学参数Table 1 Physical and mechanical parameters of soils

地裂缝的倾角取80°，管廊顶面覆土厚度取4 m。砂土换填前、后的数值模型如图7所示，其中X方向为管廊横向水平方向，取40 m；Z方向为管廊纵向水平轴向，取120 m；Y方向为竖直方向，取40 m。考虑到实际施工为明挖的工况，地裂缝设置在开挖最大深度以下，不换填工况的地裂缝设置在管廊下方，换填工况则设置在砂土下方。砂土换填是将管廊下部地裂缝两侧土体采用砂土梯形状进行换填，其中L为换填梯形底边长度，H为换填厚度，θ为换填坡角，即取换填土体两侧与竖直方向夹角。换填的宽度只要大于管廊宽度即可，为此取为管廊宽度。

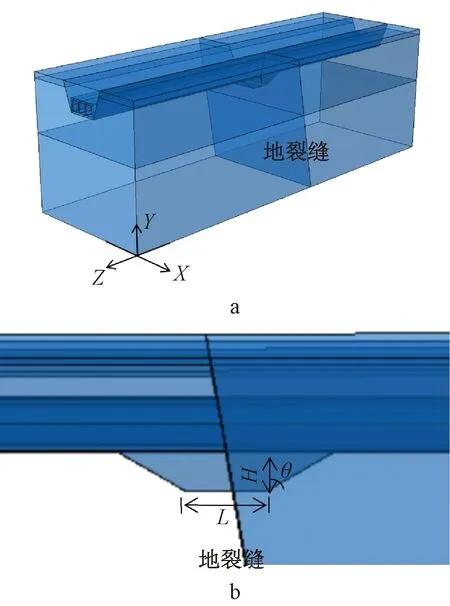
a—整体模型; b—换填砂土几何位置。图7 砂土换填后的数值模型Fig. The numerical model after being replaced with sand

2 计算结果和分析

2.1 未换填时地裂缝活动对管廊影响分析

所有工况下地裂缝均与管廊正交，且地裂缝倾角均为80°，上盘沿倾角下沉，模拟地裂缝活动对地下综合管廊的影响作用，设置未换填时上盘竖向沉降量分别为50，100，150，200 mm四种工况。地下综合管廊顶面纵向中线处在不同沉降量下的竖向位移对比见图8，可见管廊竖向差异变形显著区域均集中在地裂缝附近，且这种差异性随着沉降量的增大而加剧。

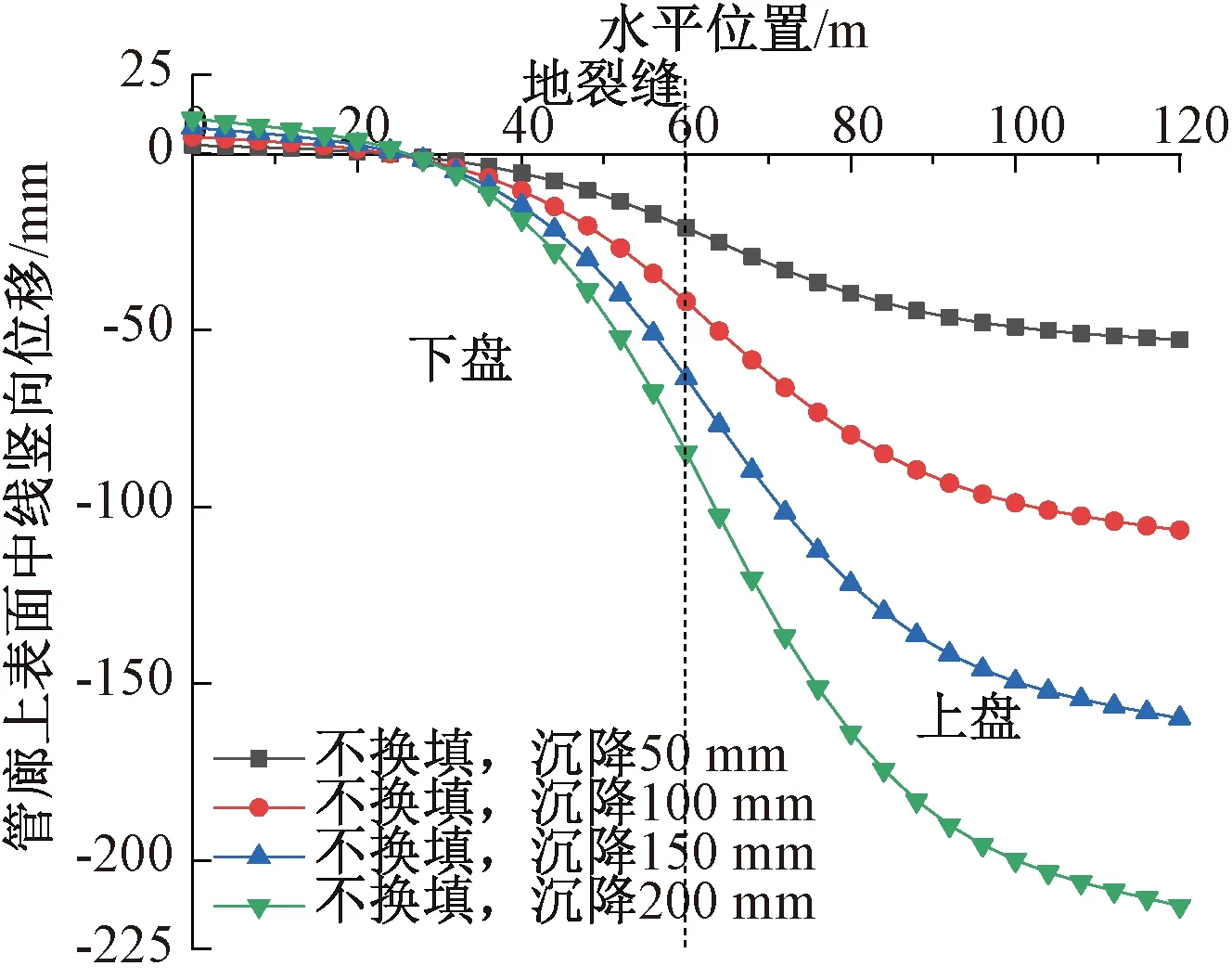
图8 管廊顶面中线竖向位移对比Fig.8 Comparisons of vertical displacement in the middle line at tops of the utility tunnel

地下综合管廊在不同竖向沉降量下的顶、底面中线处纵向应力的规律变化对比如图9、10所示。

图9 管廊顶面水平纵向应力对比Fig.9 Comparisons of longitudinal stress in the upper surface of the utility tunnel

图10 管廊底面水平纵向应力对比Fig.10 Comparisons of longitudinal stress in the bottom surface of the utility tunnel

由图9可见：管廊的纵向应力最大处出现在管廊顶面下盘靠近地裂缝处，在上盘地裂缝附近为压应力。C45混凝土的抗拉强度为3 350 kPa，当地裂缝沉降量达到100 mm，管廊顶面计算的最大拉应力已达到3 643 kPa，超过混凝土抗拉强度，实际已产生受拉破坏。

2.2 换填工况对管廊穿越地裂缝影响作用

由前面分析可知，管廊在无换填条件下、上盘沉降100 mm时的纵向拉应力已超过混凝土抗拉极限值。为研究砂土换填及不同换填厚度对管廊穿越地裂缝影响的作用效果，将地裂缝沉降量保持在100 mm不变，其他设置条件与不换填工况一致。

砂土换填的变量取换填厚度、底边长度和放坡角度。上盘竖向沉降为100 mm时，换填长度和换填坡角取经验值6 m和60°固定不变，取换填厚度分别为1，2，3，4，6，8 m进行比较。不同换填厚度下管廊的纵向应力对比如图11、12所示。由图12可见：随着换填厚度的增加，管廊纵向应力逐渐减小，换填厚度达到3 m之后，随换填厚度的增加，管廊纵向应力值降低较小，表明继续加大换填厚度的意义不大，因此，该工况下，换填厚度为3 m应是最优解，后续研究固定换填厚度为3 m不变。

图11 不同换填厚度下管廊顶面纵向应力Fig.11 Longitudinal stress in the top of the utility tunnel with different replacement thickness

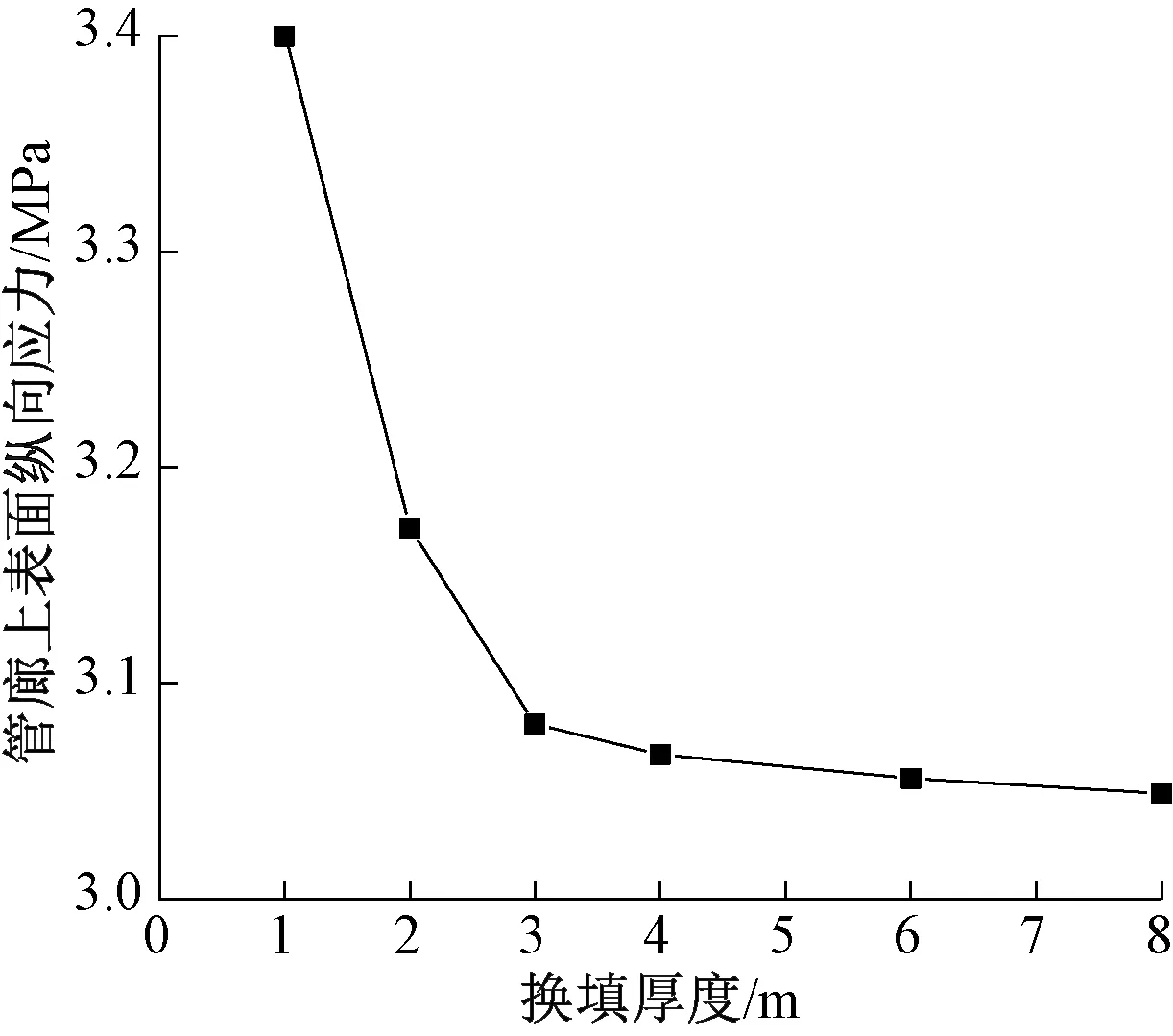
图12 不同换填厚度下管廊最大纵向应力Fig.12 The maximum longitudinal stress in the utility tunnel with different replacement thickness

换填长度分别取为2，3，4，5，6，7 m，上盘竖向沉降为100 mm时，固定换填厚度为3 m、换填坡角取60°保持不变，不同换填长度下管廊纵向应力变化如图13、14所示。可见：随着换填长度的增大，地下综合管廊最大纵向应力逐渐降低，换填长度超过6 m后管廊纵向应力降低程度逐渐放缓，考虑到实际情况，将换填长度取6 m作为后续分析的换填固定值。

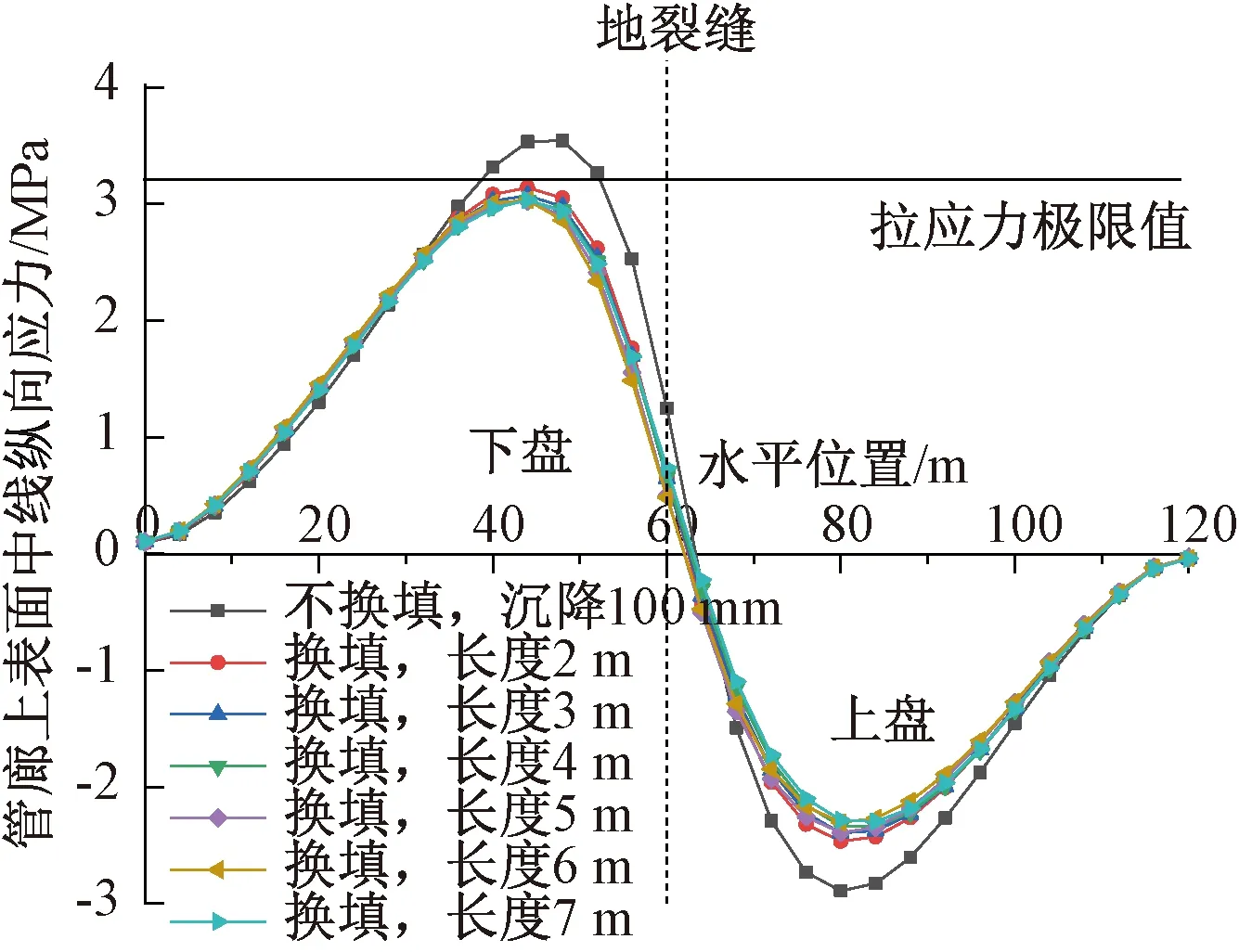
图13 不同换填长度下管廊顶面纵向应力Fig.13 Longitudinal stress in the top of the utility tunnel with different replacement length

图14 不同换填长度下管廊最大纵向应力Fig.14 The maximum longitudinal stress in the utility tunnel with different replacement length

对于换填坡角的选取，考虑到换填放坡的安全隐患，坡度不能过小，而坡度过大必将增加施工周期，因此换填坡角取为30°～60°，为更好地研究换填坡角对管廊穿越活动地裂缝的影响，分别取换填坡角为30°、37.5°、45°、52.5°、60°。固定换填长度为6 m，换填厚度为3 m不变，得到管廊纵向应力与换填坡角的关系如图15、16所示。可见，管廊最大纵向应力随着换填坡角的增大而减小，其主要原因是换填坡角增大使得管廊接触砂土的长度范围加大，有利于缓解应力的集中，考虑到管廊明挖施工，针对该工况宜取换填坡角为60°。

图15 不同换填坡角下管廊顶面纵向应力Fig.15 Longitudinal stress in the top of the utility tunnel at different replacement angles of slopes

图16 不同换填坡角下管廊最大纵向应力Fig.16 The maximum longitudinal stress of the utility tunnel at different replacement angles of slopes

2.3 砂土换填前、后地裂缝活动对地下综合管廊作用对比

上述分析结果表明，随着换填砂土的长度、厚度和坡角在一定范围内逐渐增大，管廊的最大纵向应力均出现减小的趋势，但超出一定界限后，换填效果减弱，最优的换填砂土长度、厚度和角度分别为6，3 m和60°。为了研究砂土换填前、后对管廊的作用，固定换填长度6 m、换填厚度3 m和换填坡角60°不变，研究砂土换填下地裂缝上盘沉降50，100，150，200 mm时对管廊的作用，并与不换填进行对比。

换填与未换填对管廊在不同沉降量下纵向应力和纵向应力极值影响的对比如图17、18所示。可见：换填后管廊应力分布情况基本不变，最大纵向拉应力仍出现在管廊上表面，同时换填后管廊最大纵向拉应力在地裂缝活动量为100 mm时还未达到混凝土拉应力极限值。此外，砂土换填之后管廊最大纵向拉应力相比换填之前有明显减小，减小幅度为18%，且减小幅度随着地裂缝活动量的增加而增大。

图17 换填前后管廊顶面纵向应力对比Fig.17 Comparisons of longitudinal stress in the upper surface of utility tunnels before and after replacement

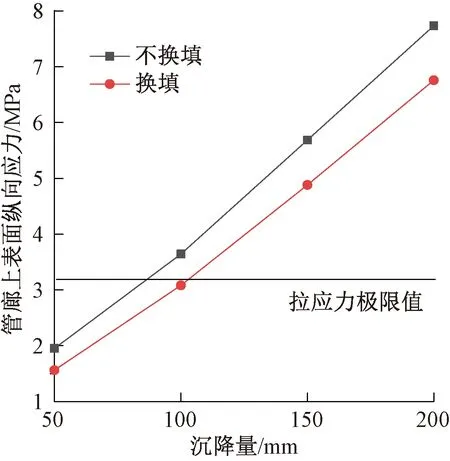
图18 换填前、后管廊最大纵向应力对比Fig.18 Comparisons of the maximum longitudinal stress in utility tunnels before and after replacement

可见砂土换填后地下综合管廊对地裂缝活动不均匀沉降的适应性较好，在地裂缝活动性较弱的区域可作为管廊穿越活动地裂缝的一种地基处理措施，能够有效减轻地裂缝活动对地下综合管廊的不利影响作用。

3 结束语

采用ABAQUS软件建立数值模型，研究砂土换填对穿越活动地裂缝的管廊应力响应变化，主要结论如下：

1)对已有矩形隧道穿越活动地裂缝的物理模型试验结果进行分析，建立其数值模型，通过对比顶部纵向应力验证了物理模型试验中矩形隧道在地裂缝活动量达到4 cm之后发生开裂，同时也验证了数值模型的有效性。

2)未换填工况下，管廊最大应力、变形均出现在地裂缝附近位置，管廊最大纵向应力出现在管廊顶部，且当地裂缝沉降量为100 mm时管廊顶部已经发生破坏。

3)随着换填砂土长度、厚度与换填坡角的增大，管廊的纵向应力逐渐降低，除换填坡角外，当换填砂土长度和厚度达到一定换填界限后，纵向应力降低放缓，表明继续换填的效果不显著。

4)增加砂土换填的长度和厚度都能够减小管廊的变形，考虑到实际换填砂土成本较高，综合管廊变形能力与实际经济效益考虑，砂土换填的最优长度为6 m，换填厚度为3 m，换填坡角为60°，该方案能将管廊最大纵向应力较不进行砂土换填时降低20%左右，因此砂土换填可作为一种管廊穿越活动地裂缝的地基处理措施。