考虑重力和黏度时变性的隧道围岩水泥浆液扩散规律研究*
韩小龙 李朝月 王 刚 杨志全 冯创成 李 明 赵灿松 张泽昊 贺 拿
王向鹏4 叶长文4 袁利伟2 杨太强5 喜文飞6 李小辉4
(1.中铁七局集团第三工程有限公司, 西安 710026; 2.昆明理工大学公共安全与应急管理学院,应急管理部地质灾害风险防控与应急减灾重点实验室,云南省高校高烈度地震山区交通走廊工程地质病害早期快速判识与防控重点实验室, 昆明 650093; 3.河南理工大学土木工程学院, 河南焦作 454003; 4.成都理工大学环境与土木工程学院,成都 610059; 5.昆明理工大学国土资源工程学院, 昆明 650093; 6.云南师范大学地理学部, 昆明 650500)
云南地处云贵高原,地形复杂多变,多为山地高原地形,山地面积占全省总面积的88.64%。随着云南公路、铁路建设的迅速发展,公路、铁路不可避免地穿越复杂地质环境,其中隧道埋设深度可从地下几米到数百米。随着隧道埋深的增加,工程环境呈现出大埋深、高水压及高地应力等特点。注浆加固技术广泛应用于隧道围岩加固,在评价隧道围岩注浆加固效果时,浆液在围岩中扩散后能否达到施工设计的有效加固范围(即形成注浆加固圈)为主要检测因素,但注浆工艺、注浆材料与地层环境等因素影响围岩中浆液扩散和注浆加固圈的形成,导致目前的注浆扩散理论并不能有效地指导工程实践[1]。
目前,国内外对于浆液扩散的研究主要集中在理论推导、模型试验和数值模拟研究等方面。在注浆理论方面,学者们基于流体力学、渗流力学和固体力学等建立了一系列理论公式,杨秀竹等建立了幂律型和宾汉姆型浆液扩散半径计算式[2-3];杨志全等建立了时变性宾汉型水泥浆液球形、柱形及柱-半球形扩散机理算式,并通过试验验证其工程适用性[4-5];叶飞等建立了考虑浆液重力的盾构隧道管片注浆扩散的计算式,分析了不同工况条件下注浆参数对浆液扩散半径的影响[6-7]。在模型试验与数值模拟方面,陈星欣等利用室内一维土柱试验,研究了重力对饱和多孔介质中颗粒运移特性的影响[8];刘健等依据模型试验,通过数值模拟系统研究水泥浆液在静水和动水两种情况下单一平面裂隙中的浆液扩散形态[9];贺玉龙等通过试验揭示了温度和有效应力对砂岩渗透率的影响机理[10];卞跃威等采用计算流体力学-离散元的耦合方法(CFD-DEM)模拟砂土注浆过程[11]。上述研究虽取得了较为丰富的研究成果,但由于模型试验的隐蔽性、模糊性、随机性和复杂性的特性,很难直观地获得浆液扩散过程,不能很好地指导实践。
为解决目前理论和模型试验研究浆液扩散规律的不足,基于固体力学和流体力学等理论,考虑注浆过程中浆液重力及黏度时变性对浆液扩散的影响,建立了浆液重力与黏度时变性耦合效应下围岩内的浆液扩散方程,结合多物理场耦合软件COMSOL Multiphysics模拟考虑水泥浆液重力及浆液黏度时变性的隧道围岩浆液扩散规律和注浆加固圈的形成全过程,分析浆液重力和注浆参数对隧道围岩浆液扩散规律及注浆加固圈形成的影响。
1 浆液重力与黏度时变性影响下渗流场-应力场方程
研究[12]表明:浆液扩散不仅与注浆参数有关,还与被注介质的物理力学性质有关,即浆液在岩土体内扩散是渗流场与应力场的耦合。
1.1 应力场方程
根据有效应力原理和应力平衡条件,可得到注浆过程固体骨架(文中假设固体为各向同性)的应力场方程[12]为:
φ▽p+f=0
(1)
其中f=[(1-φ)ρs+φρf]g
λ=Eυ/[(1+υ)(1-2υ)]
式中:E为弹性模量;υ为泊松比;εv为体应变;p为压力;f为体积力;λ为Lame系数;ρf为浆液密度;ρs为岩土体颗粒密度;φ为岩土体介质孔隙率。
可见,浆液重力(即f)和渗透体积力▽p作用于地层。渗透体积力在注浆过程中是随时间和空间变化的,在渗透场作用下的平衡方程充分体现了渗流与应力的动态耦合效应[13]。根据质量守恒定律得到注浆过程中流固耦合效应下地层应力场-渗流场方程为[13]:
(2)
其中Ks=E/[3(1-2υ)]
式中:Ks、Kf分别为岩土体骨架和浆液的体积模量;▽为拉普拉斯算子;κ为地层渗透率;μ为浆液黏度;ψ为Biot系数;t为注浆时间;Qm为浆液的源汇项;g为重力加速度;▽D为重力作用方向的向量。
1.2 渗流场方程
考虑水泥浆液重力及黏度时变特性的浆液在多孔介质中的流动特性服从Darcy’s定律方程为:
(3)
式中:u为浆液的渗流速度;μ0为浆液初始黏度;α为浆液黏度时变系数;t为时间。
将式(3)代入式(2)中,可得到考虑浆液重力与黏度时变性耦合效应下的注浆浆液扩散方程为:
(4)
2 浆液扩散规律及加固圈形成
2.1 计算原理及模型建立
以国高网G8012弥勒至楚雄国家高速公路玉溪至楚雄段在建旧寨隧道为背景,依据隧道管棚注浆模型,结合多物理场耦合软件COMSOL Multiphysics,运用 PDE 模块定义考虑浆液重力与黏度时变性耦合效应的注浆浆液扩散方程(式(1)、(3)、(4))和不考虑浆液重力与黏度时变性的注浆浆液扩散方程(式(1)、式(2)),即可得到考虑浆液重力和黏度时变性与不考虑浆液重力和黏度时变性的数值模型。为简化计算,对实际注浆工程提出如下假设:1)注浆过程中浆液流变模型不发生变化,且为不可压缩流体;2)浆液流速较小,除了在注浆孔周围局部区域浆液流态呈紊流状态外,其余位置浆液流态皆为层流。
为消除边界效应、尺寸小等影响,结合现场实际情况,确定模型宽度为50 m,高度为80 m,隧道断面形式为三心圆,径高为8.65 m,径宽为11 m。模型边界条件为:模型底部为固定约束,左、右两侧均为辊轴支承约束,隧道内部为自由约束,四周均为不透浆边界,模型及网格划分如图1所示。
依托在建旧寨隧道,采用管棚注浆加固隧道围岩的方式,隧道围岩以中风化板岩为主,其基本物理力学性质与浆液性质指标如表1所示[1,14]。
探讨不同注浆压力(0.3~1.0 MPa)和注浆时间(0~500 s)对浆液扩散的影响。模型采用瞬态模式进行计算,求解总时间设为600 s,计算时先进行地应力平衡,确保地层开始注浆加固时相应变形为零,其他相关计算参数见表1。
在注浆过程中,浆液流速为零处即为浆液扩散边界,此时注浆压力小于浆液扩散所需要的启动压力。目前,对于采用浆液扩散压力作为浆液扩散范围的判别条件还有待研究,参考文献[15]取浆液扩散压力为0.1 MPa时作为其在岩土体中扩散范围的判别条件。
2.2 浆液重力作用下浆液扩散规律
针对考虑浆液重力作用下,对重力矢量方向和其相反方向上取一个监测断面(Ⅰ—Ⅰ,如图2a所示),监测不同时刻浆液沿监测面Ⅰ—Ⅰ不同位置处的浆液扩散距离,单孔注浆浆液扩散范围如图2所示,监测面Ⅰ—Ⅰ注浆压力与距离和时间的关系如图3所示。
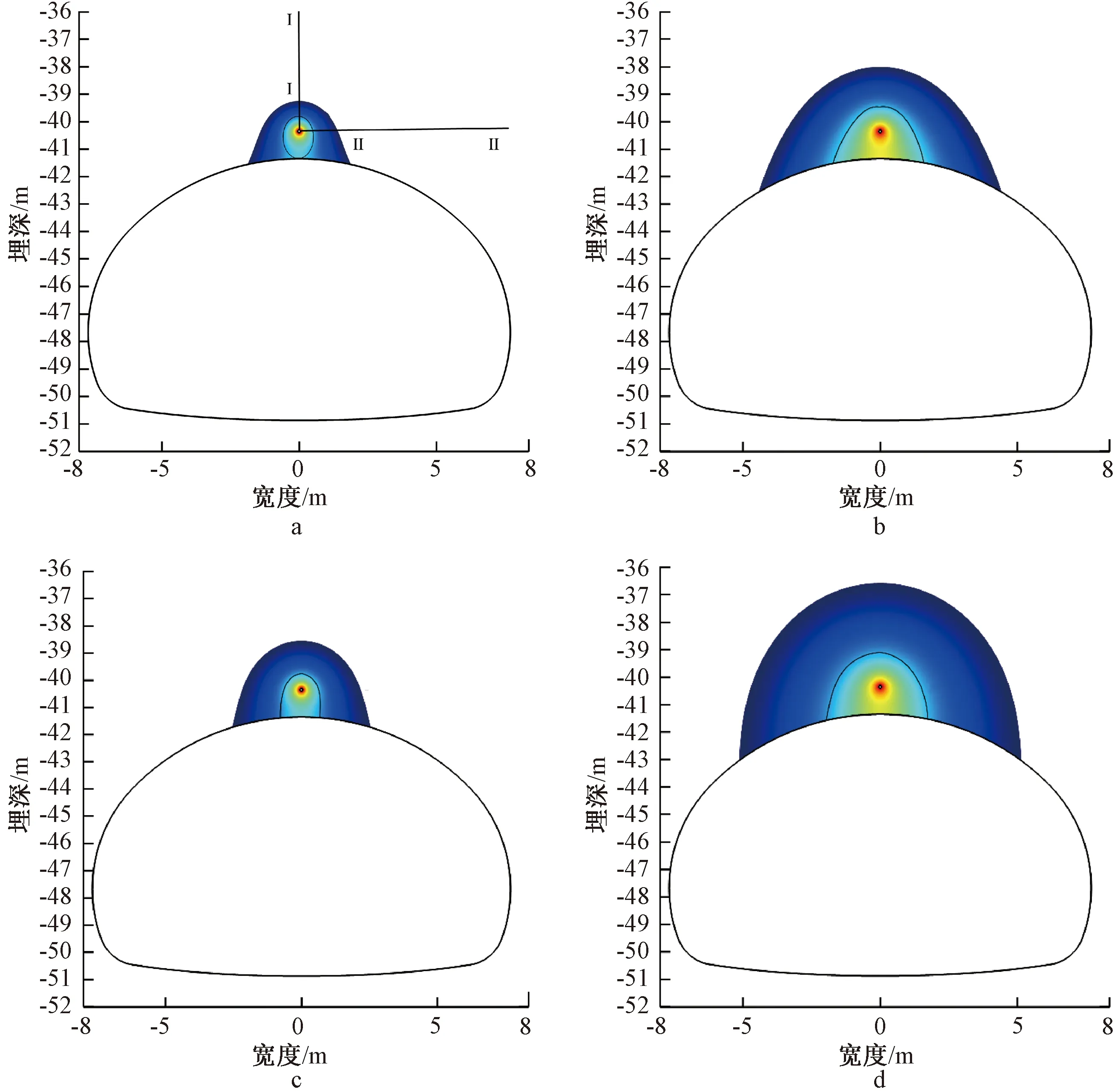
a—p=0.3 MPa,t=100 s; b—p=0.3 MPa,t=500 s; c—p=0.6 MPa,t=100 s; d—p=0.6 MPa,t=500 s。图2 单孔注浆浆液扩散范围Fig.2 Slurry diffusion ranges of single-hole grouting
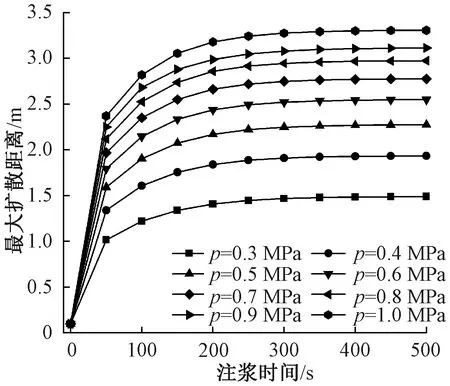
图3 监测面Ⅰ—Ⅰ注浆压力与距离和时间的关系Fig.3 Relations of grouting pressure at monitoring surface Ⅰ-Ⅰ, distances and time
得到监测面Ⅰ—Ⅰ在不同压力下t=100,500 s时的扩散距离如图2所示。可见:浆液在重力作用下浆液有效扩散形态呈椭球型,等压面也呈现出向下偏移,而未考虑重力时呈球面扩散[4];在注浆孔水平面以上浆液扩散范围远小于注浆孔水平面以下浆液扩散范围,且在注浆孔左、右两侧浆液扩散范围呈对称分布,与重力作用机制相符(即重力矢量始终竖直向下)。
结合图2、图3可以看出:增大注浆压力能显著提高浆液在围岩中的渗透性,且能显著增大浆液有效扩散距离。在重力作用下,从图2中能明显看出浆液沿重力矢量方向上的扩散距离大于其反方向上的浆液扩散距离。图3表明:注浆初期(0~100 s),浆液在注浆压力的作用下迅速扩散,注浆压力越大浆液扩散距离也越大,在注浆中期(100~200 s),浆液扩散速率显著降低,但适当延长注浆时间对浆液扩散半径仍存在促进作用,在注浆后期(200~500 s),注浆时间对浆液扩散半径的作用效果已不明显,随着注浆时间的延长,浆液最大扩散范围趋于稳定。
2.3 黏度时变性的影响
浆液黏度随时间呈非线性变化大,注浆时间越长,浆液扩散距离增长越来越慢,黏度增大到一定程度后,浆液在注浆压力和重力作用下便不再扩散。因此,取黏度时变性系数α分别为0.01、0.02、0.03、0.04,通过对监测断面Ⅱ—Ⅱ(图2a)获取数据,分别得到考虑或不考虑浆液黏度的浆液扩散距离的差异以及不同时变性系数对单孔注浆作用下浆液扩散距离的影响。考虑或不考虑时变性扩散距离差异如图4所示,不同时变性系数浆液扩散距离如图5所示。
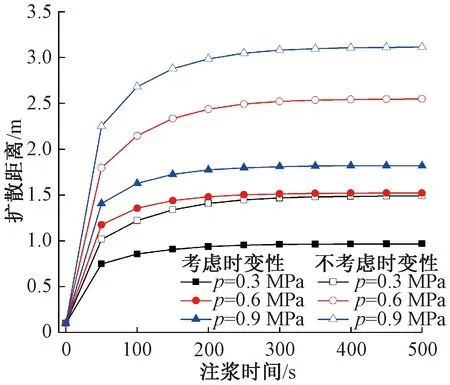
图4 注浆压力下浆液扩散距离Fig.4 Slurry diffusion distances under grouting pressure

图5 时变性系数的影响Fig.5 Influence of variability coefficients
图4、图5可以看出:考虑浆液黏度时变性时的扩散距离明显小于不考虑浆液黏度时变性时的扩散距离;随着黏度时变性α的增加,浆液扩散距离显著减小,且浆液达到最终扩散距离时所需的注浆时间也就越小。
因此在隧道施工过程中,应考虑浆液重力效应与黏度时变性对浆液扩散距离及扩散形态的影响,从而保证隧道围岩的稳定性和可靠性。
2.4 管棚注浆加固圈形成规律
管棚注浆加固圈的形成主要由注浆管注浆参数、外倾角及埋设角度等因素影响,依据前文研究,分析管棚注浆方案在注浆压力0.5 MPa、注浆时间200 s的施工参数下注浆管埋设角度对注浆加固圈的影响。选取注浆管埋设角度为10°、20°、30°、40°分布对应在隧道中轴线两侧,不同注浆管埋设角度下注浆加固圈厚度见表2所示,不同注浆管埋设角度下浆液扩散范围如图6所示。

a—θ=10°; b—θ=20°; c—θ=30°; d—θ=40°。图6 不同注浆管埋设角度下注浆加固圈形态Fig.6 Forms of grouting reinforcement rings at different angles of grouting pipes
参照施工设计文件,浆液有效注浆范围为隧道开挖线径向2 m,因此,取浆液扩散距离大于等于2 m并形成的闭环的范围为注浆加固圈。由图6、表2表明:注浆加固圈的分布分为与注浆管埋设角度密切相关,不同注浆管埋设角度形成的注浆加固圈形态各异,注浆管埋设角度从10°增加35°时,注浆加固圈的厚度从5.52 m减小2.25 m,能够达到设计注浆加固圈有效扩散范围,当注浆管埋设角度大于35°时,形成无效注浆加固圈或未形成注浆加固圈,表明施工中,注浆管埋设角度不宜大于35°。
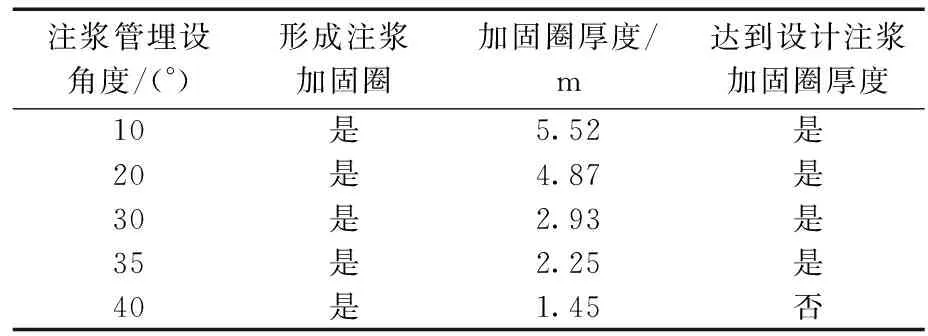
表2 不同注浆管埋设角度下注浆加固圈厚度Table 2 Thicknesses of the grouting reinforcement ring at different angles of grouting pipes
3 工程应用
3.1 工程概况
国高网G8012弥勒至楚雄国家高速公路玉溪至楚雄段玉溪市峨山县岔河乡在建旧寨隧道,为分离式长隧道,右线长度为2 256 m,最大埋设为339 m,左线长度为2 243 m,最大埋深为332 m,累计总长度为4 499 m,该隧道地质结构复杂,围岩多变,突泥涌水频发,施工安全风险高,难度大。现场勘查围岩为中风化板岩,岩体较破碎降雨状态下洞室内地下水可能呈点潮湿状或点滴状出水,采用TB 10049—2004《铁路工程水文地质勘察规程》推荐的降水入渗法预测隧道正常涌水量为1 011 m3/d,隧道涌水量较大,容易造成隧道在渗透力作用下失稳,为了确保隧道开挖的顺利进行以及后续隧道运营围岩的长期稳定,选择超前小导管、辅助锚杆等联合支护方法来加固隧道,故对该隧道进行注浆加固隧道围岩。但在施工后检测发现常规的注浆加固方案得到的注浆加固圈厚度不达标,因此,对现场注浆设计进行了优化。
3.2 注浆加固方案与效果
结合现场实际注浆施工情况,依据前文模拟计算结果,设计注浆压力为0.5 MPa,注浆时间保持在为300 s,注浆管采用长4.5 m的φ89×6热轧无缝钢管,采用梅花桩布设方式,环向埋设角取20°,以5°~15°外倾角打入拱部围岩,采用水灰比为1∶1水泥浆液。
现场注浆后,使用美国GSSI公司生产的SIR-3000型地质雷达,天线频率900 MHz,测线以缺陷区延长2 m测线呈“井”字形加密布置检测,并进行压水试验,表明等检测表明围岩整体性和连续性得到了显著提高,监测得到拱顶沉降均小于5 cm,在可控范围内,围岩注浆加固效果明显,已达预期效果。
在开展考虑水泥浆液重力与黏度时变性的隧道围岩浆液扩散规律及工程应用研究时假设该工程的中风化板岩为各向同性介质,但在实际工程中该中风化板岩满足典型的各向异性特征,据此得到的研究结论与实际工况仍有一定的差异。因此,对各向异性岩土体中注浆理论的研究是下一步亟需进行的工作。
4 结束语
1)基于固体力学和流体力学等理论,考虑注浆过程中水泥浆液重力及黏度时变性对浆液扩散的影响效应,建立了考虑浆液重力与黏度时变性耦合效应下的注浆浆液扩散方程;依托多物理场耦合软件COMSOL Multiphysics模拟了考虑水泥浆液重力及浆液黏度时变性的隧道围岩浆液扩散规律和注浆加固圈的形成,分析浆液重力和注浆参数对隧道围岩浆液扩散规律及注浆加固圈形成的影响,为现场注浆设计和施工提供参考。
2)在浆液重力作用下,浆液沿重力矢量方向上的扩散距离大于其反方向上的浆液扩散距离,浆液有效扩散形态呈椭球型,等压面也呈现出向下偏移,而未考虑重力时浆液呈球面扩散。
3)注浆加固圈的分布形态与注浆管的埋设角度密切相关,注浆管埋设角度越小,注浆加固圈的厚度越大,但容易造成浆液浪费,因此合理地布设小导管是获得有效注浆加固圈的关键。

