节理岩体对盾构开挖稳定性和地层损失率的影响*

李 婷 姜谙男 张峰瑞 钟 越 徐 波

(1.大连海事大学道路与桥梁工程研究所， 辽宁大连 116026； 2.南昌轨道交通集团有限公司， 南昌 330013)

隧道的开挖会引起周围土体变形和地层损失，土体变形和地层损失率过大，可能会引发塌方等事故。目前多数隧道地层损失率的数值模拟采用各向同性模型，而实际工程中，岩体中往往含有大量节理，节理的存在破坏了岩体的连续性和完整性，使得数值模拟与实际工程存在较大的误差[1-2]。因此，为了确保节理岩体中隧道的施工安全，研究节理岩体隧道的稳定性和地层损失率非常必要。

对于节理岩体的稳定性，国内外学者已开展了大量的研究工作。杨忠民等采用3DEC软件进行数值模拟，对节理围岩的变形状态进行研究[3]。袁铁等通过FLAC3D软件建立数值模型，发现压剪应力在节理倾角为45°时最小，在75°时压剪应力最大[4]。彭双喜利用有限元强度折减法为节理岩体隧道的稳定性分析提供了一个量化标准[5]。唐正东得出了在施工中应重点关注隧道与节理相交部位的结论[6]。刘红兵分析了不同倾角岩层产生偏压作用的规律[7]。王永甫等通过PLAXIS程序模拟，提供了一种稳定性分析的计算方法[8]。许崇帮等得到了节理产状与围岩变形的特征[9]。何长江等采用有限元强度折减法, 研究了不同节理倾角对顺层隧道稳定性的影响[10]。

近年来针对地层损失率也有许多研究。韩煊等对国内多条隧道的地层损失率进行分析，得到隧道地层损失率的范围[11]。丁智等研究了双线隧道在软土地区的地层损失率[12]。周健等通过FLAC2D软件进行数值模拟，提出了最佳施工方案[13]。白永学等研究成都地区砂卵石地层的地层损失，提出了相应的施工对策[14]。王建秀等研究盾构施工与地层损失率的关系[15]。丁智等研究了不同施工参数对软土双线盾构掘进引起的土体竖向变形的影响[16]。包小华等构建了三维数值计算模型，分析施工参数对地表变形的影响[17]。邹飞等研究节理间距对地层损失率的影响[18]。袁长丰等采用相似材料模拟试验得到了地表沉陷的概率分布规律[19]。

在以上研究成果中均未见到对节理岩体隧道地层损失率的研究。南昌某隧道受节理切割严重，使围岩的完整性受到不同程度的破坏，对隧道稳定性和地表变形产生严重的影响。因此以南昌地铁盾构隧道为工程依托，采用UDEC[20-21]软件建立数值模型，研究节理倾角对隧道围岩变形、塑性区和地表沉降的影响，在此基础上通过双线Peck曲线分析地层损失率的变化范围，并且分析节理间距、盾构隧道间距以及隧道埋深对地表沉降的影响，为节理隧道施工提供参考。

1 盾构施工相关计算理论

1.1 非连续介质计算原理

对岩体进行数值模拟主要有两种方法：连续介质方法和非连续介质方法。连续介质方法在假设小变形的前提下，通过设置节理单元的方法能够处理极少部分的不连续结构面，但对于处理大多数不连续结构面的问题时，应采用非连续介质方法。

非连续介质方法将岩体看成是由节理等结构面切割而成的刚性块体或者可变形块体，接触主要是块体与块体之间形成角、面和边，块体与块体之间的节理面构成节理岩体。块体可以平移、转动或者变形，节理面可以被压缩、分离、滑动，运用牛顿第二定律描述块体之间发生的运动，因此，可认为节理岩体是非连续性介质，采用非连续介质方法可以较为真实地体现出节理岩体中的大变形特征。

1.2 岩石节理本构模型

将完整岩石基质按各向同性的均匀线弹性材料处理，对于一般受力下岩体的屈服，可以用摩尔-库仑准则来表示：

τ=c+σtanφ

(1)

式中：τ为抗剪强度；c为黏聚力；φ为内摩擦角。

Jeager 等建立了首个节理岩体强度模型，对于只有一组均值且各向同性节理的岩体来说，其力学性质主要受节理面方向所控制[22]。设β为节理面外法线与最大主应力方向的夹角，与节理的倾角相同(图1)。在第一主应力σ1与第三主应力σ3作用下，节理面上的正应力与剪应力表达式为:

图1 节理岩体Fig.1 Jointed rock masses

(2)

将式(2)中的正应力σ和剪应力τ代入式(1)，整理后可以得到：

(3)

对β求一阶导数，并令其为 0，得:

(4)

可以求得当β=45°+φ/2时，(σ1-σ3)取得最小值，而在摩尔应力圆上最大抗剪强度τmax=(σ1-σ3)/2，即当节理倾角为45°+φ/2时，取得最大抗剪强度的最小值。

1.3 盾构隧道沉降预测的经验算式

Peck通过对大量实际工程数据的数理统计分析，对不排水情况下单线隧道施工过程中地表沉降进行了总结，指出隧道上方的地面沉降槽形状呈正态分布规律，即著名的Peck公式[23]，可用式(5)来表述，Peck 公式后来逐渐成为研究双线盾构隧道沉降问题的理论基础和重要参考。

(5)

式中：S(x)为沉降槽上某x点的地面沉降值；Smax为地面最大沉降值；i为隧道沉降槽宽度。

假定地层不排水，对式(5)进行积分,得到土体单位长度损失量：

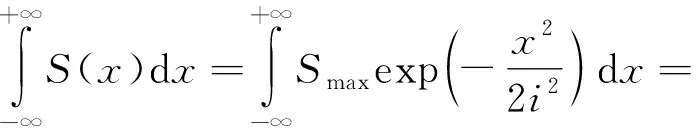
(6)

由式(6)反推可以得到地面最大沉降值：

(7)

式中：R为隧道半径；η为地层损失率。

通过式(5)～(7)可以得到沉降计算式：

(8)

由于主要研究节理岩体的倾角对盾构隧道地表沉降的影响，故假定无二次扰动效应，假定双线的土体损失率与沉降槽宽度相同。分别求出先行洞和后行洞的地表沉降曲线，然后叠加，就可以得到盾构隧道的地表沉降曲线[24-25]。

根据叠加原理，由式(8)可以得到盾构隧道的沉降值：

(9)

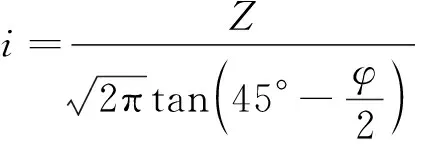
式中：i1为先行洞沉降槽宽度；i2为后行洞沉降槽宽度；Z为隧道深度；φ为摩擦角；η1为先行洞地层损失率；η2为后行洞地层损失率；L两个隧道的中心距离。

2 工程概况

南昌某地铁区间为双孔圆形隧道，隧道顶部埋深9.8～15.5 m，内径为5.4 m，外径为6.0 m，管片宽为1.2 m，管片厚度为0.3 m，双线距离为14 m。区间隧道穿越部位地层主要有砂砾、强风化泥质粉砂岩、中风化泥质粉砂岩层，局部粗砂层，岩体较完整。在长期的分化作用下，地质构造较发育，不同地区的岩层产状也不同，各区段之间岩层的节理倾角差异显著。根据钻孔揭示(图2)，场区范围内基岩主要为中风化泥质粉砂岩，局部可见钙质泥岩充填，节理间距为1～3 m，延伸长度为0.5～2.0 m。根据现有的地质资料和现场地质勘测，岩石基本质量等级为Ⅳ级。

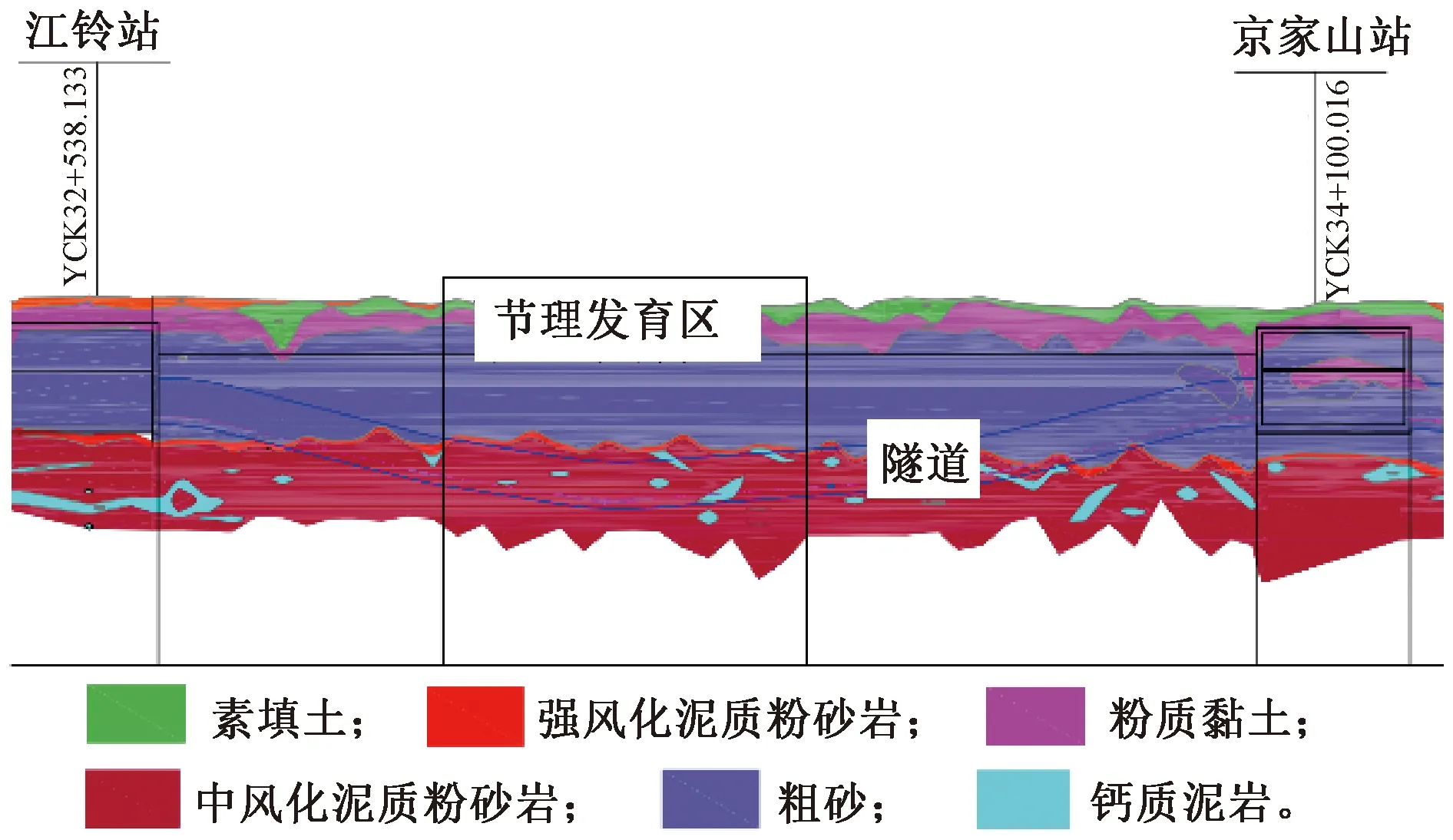
图2 工程地质剖面Fig.2 The geological profile of the site

3 数值模拟

3.1 数值模型的建立

采用UDEC离散元软件建立数值模型，两条隧道的几何参数一致,隧道埋深为16.0 m，内径为5.4 m,外径为6.0 m，管片宽为1.2 m，管片厚度为0.3 m，注浆圈的厚度为0.3 m,隧道间隔为14.0 m，节理间距为2.0 m，模型宽度为62 m,高度为38 m。由于重点考虑节理倾角对隧道稳定性和地层损失率的影响，将地层简化，忽略上部土层的影响，只考虑岩石层，模型中所采用的力学参数主要是通过现场试验和地勘资料所测得的数据。

施加边界条件限制,模型底部边界为固定端，约束左、右边界法向位移，顶部边界为自由边界条件。在模拟开挖前，运行足够多的迭代循环以达到在重力作用下的初始平衡状态，之后开挖隧道。岩体采用摩尔-库仑弹塑性模型，节理的本构模型关系选取库仑滑移模型，添加倾角0°、30°、45°、60°和90°的虚拟节理，模型如图3所示。

图3 盾构隧道数值模型 mFig.3 The numerical model of the shield tunnels

模拟过程：借助 block 命令生成节理岩体平面轮廓，利用命令 crack 生成节理面，用 mat 和 jmat 命令赋予岩块与节理面力学参数，布置监测点，进行开挖后，输出位移云图和监测的位移。

3.2 参数选取

根据室内试验和现场实际勘测资料，并结合 JTG 3370.1—2018《公路隧道设计规范》和《工程地质手册》[24]中对现场工程地层的物理力学参数的取值如表1和表2所示。

表1 节理参数Table 1 Joint parameters

表2 模型参数Table 2 Model parameters

4 数值结果分析

4.1 隧道围岩变形结果分析

由不同倾角下的竖向位移沉降云(图4)可见：地下岩体由于重力作用相互挤压，达到平衡状态。在隧道的开挖过程中，部分岩体受到扰动，破坏了地应力的平衡，使得地应力重新分布。在地应力重新分布的过程中，拱顶岩块出现了松动脱离，拱底被挤压，拱顶表现为沉降，拱底表现为隆起，拱腰的两侧收敛。岩体沿节理面发生滑动，隧道围岩在节理面发生变形，节理面变形明显增大。当节理倾角为0°时，隧道的围岩变形发生在两个拱肩上且沿隧道竖向中线两侧对称分布；当节理倾角为30°、45°和60°时，围岩变形随着倾角的变化，分布在节理的上、下部分；当节理倾角为90°时，拱顶出现沉降，围岩在拱顶中间发生变形。且由图4可知：0°和90°的围岩变形沿隧道竖向中线两侧对称分布，30°、45°和60°的围岩变形随着倾角的变化呈非对称分布。

a—节理倾角为0°； b—节理倾角为30°； c—节理倾角为45°； d—节理倾角为60°； e—节理倾角为90°。图4 不同节理倾角的隧道围岩变形 mmFig.4 Contours for deformation of surrounding rock at different dip angles

4.2 塑性区计算结果

不同倾角下的塑性区分布如图5所示。围岩塑性区的分布情况随着节理倾角的改变而发生变化，节理岩体塑性破坏发展的方向与节理倾角的方向基本一致。

因隧道开挖后破坏区首先沿洞周节理面的位置形成滑动面发生破坏，即节理面是隧道围岩的薄弱环节，需引起重视。节理倾角为45°时，隧道围岩塑性区范围最小，隧道最为稳定，节理倾角为60°和90°时，隧道围岩塑性区范围较大，隧道不稳定，要引起注意，加强对60°和90°节理围岩的支护。

a—节理倾角为0°； b—节理倾角为30°； c—节理倾角为45°； d—节理倾角为60°； e—节理倾角为90°。图5 不同节理倾角的塑性区Fig.5 Plastic zones at different dip angles

由表3可以得到不同塑性区块体数与模型单元总块体数的比值，如图6所示。分析得出节理倾角为45°时，屈服临界块体占总块体数的比值最小，而在90°时取得最大值，在60°时次之；节理倾角为30°时，已经屈服块体占总块体数的比值最小，而在90°时取得最大值，在60°时次之；节理倾角为45°时，发生张拉破坏块体数占模型总块体数的比值最小，而在90°时取得最大值。说明节理倾角为30°和45°时，围岩不易失稳，节理倾角为60°和90°时，围岩有较大可能失稳。

图6 不同节理倾角塑性区比值Fig.6 Ratios of plastic zones in the overall zone at different dip angles

表3 不同节理倾角的塑性区统计Table 3 Statistics of plastic zones with different dip angles

4.3 地表沉降计算结果

不同倾角下的地表沉降曲线见图7。沉降曲线呈单峰状或双峰状的形式，最大地表沉降值均位于隧道中心正上方，曲线的沉降趋势基本一致。地表沉降的位移分布明显受到节理面倾角的影响。当节理倾角为0°时，地表沉降曲线呈现左、右对称分布，地表最大沉降值为 4.590 mm；当节理倾角为30°时，地表沉降曲线呈现非对称分布，地表最大沉降值在右洞拱顶的上方，为5.409 mm；当节理倾角为45°时，地表沉降曲线开始往左偏移，地表最大沉降值为 4.490 mm；当节理倾角为60°时，地表最大沉降值在左洞拱顶的上方，为6.261 mm；当节理倾角为90°时，地表沉降曲线再次呈现左、右对称分布，地表最大沉降值为5.189 mm。其中拱顶最大竖向位移为6.261 mm，拱顶最小竖向位移为4.490 mm。在当节理倾角为0°～45°或45°～90°时，沉降随着倾角的变化呈先增大后减小的趋势，节理倾角在60°左右时沉降值最大, 隧道的稳定性最差, 节理倾角对岩体强度的影响最大；节理倾角在45°左右时沉降值最小, 隧道的稳定性最好, 节理倾角对岩体强度的影响不大。

图7 不同倾角节理的地表沉降值Fig.7 Subsidence at different dip angles

在隧道施工过程中应注意观察节理走向，并采取相应的支护方案进行加固，保证盾构施工安全顺利进行。

4.4 Peck 曲线及地层损失率分析

借助 Peck 公式对双线隧道进行地面沉降的预测时，需要测得地质条件的相关参数，但是不同地质条件的相关参数具有特殊性。而现有的大多数沉降预测主要依赖于地方经验确定地层体积损失率和沉降槽宽度，有着很大的局限性。根据前面模拟的沉降值，借助Oringin软件，拟合出该工程的地表沉降曲线，如图8所示。可知：监测沉降点基本都分布在曲线周围，决定系数R2均大于0.95，拟合效果较好。根据拟合曲线和式(8)可反算出左、右线隧道地层损失率：当节理倾角为0°时，地层损失率为 0.675%(左线)和0.673%(右线)，地层损失率均值为0.674%；当节理倾角为30°时，地层损失率为0.723% (左线)和 0.796%(右线)，地层损失率均值为0.759%；当节理倾角为45°时，地层损失率0.661%(左线)和 0.655%(右线)，地层损失率均值为0.658%；当节理倾角为60°时，地层损失率0.921%(左线)和 0.870%(右线)地层损失率均值为0.896%；当节理倾角为90°时，地层损失率0.762%(左线)和 0.764%(右线)，地层损失率均值为0.763%。

a—0°节理倾角； b—30°节理倾角； c—45°节理倾角； d—60°节理倾角； e—90°节理倾角。 拟合曲线； 模拟值。图8 不同节理倾角下沉降拟合曲线Fig.8 The mean values of ground loss ratios at different dip angles

由图9可知：在60°倾角时取得最大地层损失率均值为0.896%，在45°倾角时，取得最小地层损失率均值为0.658%，该地区的地层损失率均值为0.658%～0.896%，在合理范围[11]内。在0°～45°或45°～90°地层损失率随着倾角的变化呈现先增大后减小的趋势，倾角为45°时地层损失率最小，倾角为60°时地层损失率最大。主要原因是：当围岩节理倾角以45°为主时，岩体产生屈服并且发生张拉损伤，使得岩体发生拉剪混合破坏及剪切破坏，节理倾角以60°为主时，主要受自重作用和剪切作用，隧道顶部及拱腰也产生了破裂面，增加土体扰动的次数。特别倾角为90°时，隧道在洞顶正中形成了贯通的塑性破裂面，剪切破坏减少，减少土体的扰动。

图9 不同节理倾角的地层损失率均值Fig.9 The mean values of ground loss ratios at different dip angles

4.5 实际监测与模拟结果对比

为充分验证模型的合理性,在研究区段内选择节理倾角主要为60°的地表沉降的实际监测数据与模拟值进行对比,如图10所示。

图10 模拟值与实测值对比Fig.10 Comparisons between the simulated and measured

可见：模拟值与地表沉降实测值之间的吻合度比较好,均呈双峰状，实测值稍微大于模拟值。左线隧道模拟最大沉降值为6.261 mm,右线隧道模拟最大沉降值为5.915 mm, 左线隧道实测最大沉降值为7.176 mm，由线隧道实测最大沉降值为6.602 mm。可见，模型对该工程具有良好的适用性。

5 沉降曲线的规律性分析

5.1 不同倾角、埋深对地表沉降的影响

在节理间距为20 m、隧道间距为14.0 m的情况下，不同倾角、埋深的地表沉降曲线如图11所示。可见：节理倾角为0°和90°时，地表沉降值呈对称分布，受节理倾角的影响，节理倾角为30°、45°和90°时，地表沉降值呈非对称分布。当隧道埋深在d和2d(d为隧道直径)时，地表沉降值随着节理倾角的增大而增大，当隧道埋深在3d、4d和5d时，地表沉降的最大值出现在节理倾角为60°的情况下。

a—埋深为d； b—埋深为2d； c—埋深为3d； d—埋深为4d； e—埋深为5d。 节理倾角0°； 节理倾角30°； 节理倾角45°； 节理倾角60°； 节理倾角90°。图11 不同倾角、不同埋深的地表沉降值Fig.11 Subsidence with different buried depths and at different dip angles

当隧道埋深在2d～3d时，沉降曲线开始发生变化，地表沉降曲线由双峰状向单峰状过渡，当隧道埋深在d和2d时，沉降曲线呈双峰状。当隧道埋深在3d时，不同倾角的沉降曲线呈双峰状和单峰状同时存在的情况。当隧道埋深在4d和5d时，不同倾角的沉降曲线呈单峰状。同时开挖工况下双线隧道引起的地表沉降曲线变化形态呈对称分布，在呈双峰状的沉降曲线中，最大沉降值均出现在每个隧道中心的正上方，在呈单峰状的沉降曲线中，最大沉降值均出现在隧道中心轴线的正上方。随着埋深的增加，地表沉降值逐渐降低，但减小的趋势随埋深增加会逐渐放缓。这主要是由于当隧道的埋深相对较浅,使得围岩在其中的承载力并没有得到很好的发挥。随着隧道埋深的增大，围岩在其中的自重应力和承载力均会有所增大,但是围岩承载力的增加速度大于围岩中自重应力的增加速度,最终体现为隧道中地表的沉降量将随着隧道围岩埋深的增加而有所减少。

5.2 不同倾角、隧道间距对地表沉降的影响

在隧道埋深为16 m、节间间距为2.0 m的情况下，不同倾角、隧道间距的地表沉降曲线如图12所示。可见：当区间隧道间距为在d和3d时，地表沉降值随着节理倾角的增大而增大，当区间隧道间距在2d时，地表沉降的最大值出现在节理倾角为60°的情况下，而最小值出现在节理倾角为45°的情况下。

a—隧道间距为1.5d； b—隧道间距为2d； c—隧道间距为2.5d。 节理倾角0°； 节理倾角30°； 节理倾角45°； 节理倾角60°； 节理倾角90°。图12 不同倾角、不同隧道间距的地表沉降值Fig.12 Subsidence with different tunnel spacing and at different dip angles

随着隧道间距的增大，地表沉降逐渐降低，但减小的趋势随埋深增大会逐渐放缓。这是因为，双线隧道的间距越大，其相对中心点的扰动和作用就越弱,在共同中心点的扰动范围内沉降的变形就会逐渐减弱，可以认为是两条单线隧道独立开挖然后再进行叠加，进而导致地表沉降曲线呈现双峰。随着隧道间距的减小，施工的相互干扰影响的程度增强，使地表下沉降的曲线逐渐呈现为单峰状。

5.3 不同倾角、节理间距对地表沉降的影响

在隧道间距为14 m、埋深为16 m的情况下，不同倾角、不同节理间距的地表沉降曲线，如图13所示。可见:节理间距为1.0 m时，最大地表沉降值出现在节理倾角为90°的情况下，最小地表沉降值出现在节理倾角为45°的情况下；节理间距为1.5 m时，最大地表沉降值出现在节理倾角为90°的情况下，最小地表沉降值出现在节理倾角为45°的情况下；节理间距为2.0 m时，最大地表沉降值出现在节理倾角为60°的情况下，最小地表沉降值出现在节理倾角为45°的情况下；节理间距为2.5 m时，最大地表沉降值出现在节理倾角为60°的情况下，最小地表沉降值出现在节理倾角为45°的情况下；节理间距为3.0 m时，最大地表沉降值出现在节理倾角为60°的情况下，最小地表沉降值出现在节理倾角为45°的情况下。由此可见，在隧道间距为14 m、埋深为16 m的情况下，节理倾角为60°和90°容易失稳，而节理倾角为45°最不容易失稳。

图13 不同倾角、不同节理间距的地表沉降值Fig.13 Subsidence with different joint spacing and at different dip angles

随着节理间距的增加，地表沉降逐渐增大，但增大的趋势随埋深增加会逐渐放缓。这是因为，节理间距越大，岩体的强度越大，越接近于整体岩石强度，因扰动产生的沉降值越小。

6 结束语

1)节理面削弱了盾构隧道围岩的稳定性，容易在节理面出现滑动；围岩变形在0°和90°时呈对称分布，在30°～60°呈不对称分布。

2)盾构隧道围岩塑性区范围随着节理倾角的改变而变化，节理岩体塑性区的发展方向与节理倾角方向基本一致；当节理倾角为30°～60°时开始产生偏压；节理倾角为60°最容易失稳，与在β=45°+φ/2时取得最大抗剪强度的最小值的理论相符合，验证了数值模拟的正确性。因此开挖前应结合节理面倾角预先确定重点监控部位，确保隧道围岩在开挖过程中施工安全。

3)节理岩体双洞盾构隧道开挖引起地表沉降曲线，呈双峰状，地表沉降最大值都是在隧道中心位置；地表沉降曲线在0°和90°时呈对称分布，在30°、45°和60°呈不对称分布；在0°～45°和45°～90°沉降值随着倾角的变化呈现先增大后减小的趋势，倾角为45°时地表沉降最小，倾角为60°时地表沉降值最大，实测值与模拟值较为相符，施工时应对节理倾角为60°和90°的岩体部位加强注浆控制。

4)由拟合出来的地层损失率可知，该工程地段的地层损失率为0.658%～0.896%；在0°～45°和45°～90°地层损失率随着倾角的变化呈现先增大后减小的趋势，地层损失率随着地表沉降值的增大而增大。

5)通过模拟不同倾角在不同的隧道埋深、不同的隧道间距以及不同的节理间距的情况下，发现地表沉降值与隧道埋深、隧道间距以及节理间距呈反比例关系，而在不同节理倾角的条件下，地表沉降值表现出不同的规律性。