Effect of Magnetic Field on Forced Convection between Two Nanofluid Laminar Flows in a Channel

Afrasiab Raisi and Ahmad Qanbary



Effect of Magnetic Field on Forced Convection between Two Nanofluid Laminar Flows in a Channel

Afrasiab Raisi*and Ahmad Qanbary

This paper provides a numerical study of forced convection between hot and cold nanofluid laminar flows that are separated by a thin membrane, in a horizontal channel. Outer surface of channels’ walls are thermally insulated and divide into two parts; namely NMP and MP. NMP is the channel’s wall from the entrance section to the middle section of channel that is not influenced by magnetic field. MP is the channel’s wall from the middle section to the exit section of channel which is influenced by a uniform-strength transverse magnetic field. The governing equations for both hot and cold flows are solved together using the SIMPLE algorithm. The effects of pertinent parameters, such as Reynolds number (10≤≤500), Hartman number (0≤≤60) and the solid volume fraction of copper nano-particles (0≤≤0.05), are studied. The results are reported in terms of streamlines, isotherms, velocity and temperature profiles and local and average Nusselt number. The results of the numerical simulation indicate that the increase in Reynolds number and the solid volume fraction lead to increase in Nusselt number. Meanwhile, the results also show that the rate of heat transfer between the flows increases as the Hartmann number increases, especially at higher values of the Reynolds number.

magnetic field, forced convection, nanofluid, membrane, channel

1 Introduction

In order to save the energy consumption in various industries, including the automotive, electronics, aerospace, food processing and manufacturing industries, the heat exchangers that are used must be smaller and lighter and also with higher thermal performance. Due to restrictions on the size of the heat exchangers, the heat exchange surface cannot be increased. The use of fluids that have better heat transfer characteristics is a good way to increase the efficiency of such heat exchangers. Nanofluid is a suspension of solid nanoparticles in conventional base fluids such as water, oil or ethylene glycol, and has a higher thermal conductivity than the base fluid depending on the shape, size and type of the solid nanoparticles[1–5].

In recent years, forced convection of nanofluids in different channels has been investigated by several researchers. Izadi, et al[6], numerically investigated laminar forced convection of alumina-water nanofluid in an annulus. Their findings showed that adding nanoparticles to the base fluid increased the convective heat transfer coefficient, but had a little effect on the velocity profile. Bianco, et al[7], numerically studied the developing laminar forced convection flow of a water–Al2O3nanofluid in a circular tube, submitted to a constant and uniform heat flux at the wall. They showed that the single and two-phase models led to the same results and the temperature dependent models presented higher values of heat transfer coefficient and Nusselt number. Santra, et al[8], examined laminar forced convective heat transfer of copper-water nanofluid in a horizontal parallel plate channel. For this purpose, the nanofluid was considered as Newtonian as well as non-Newtonian. They concluded that the thermal behavior of Newtonian and non- Newtonian nanofluid was more or less the same. Also, the sharp increase in the wall shear stress with increasing the solid volume fraction for non- Newtonian nanofluid, was one of their outcomes. Manca, et al[9], reported the results of an investigation on forced convection with Al2O3-water nanofluids in a two dimensional channel under uniform heat flux condition. In their report an increase in the heat transfer coefficient and required pumping power as solid volume fraction increases was confirmed.

SAha, et al[10], presented a numerical investigation of turbulent forced convection flow of water based Al2O3and TiO2nanofluids flowing through a horizontal circular pipe under uniform heat flux boundary condition applied to the wall. Based on the results of this study, with increasing Reynolds number and solid volume fraction and decreasing size of nanoparticles, Nusselt number increased.

In experimental research Peyghambarzadeh, et al[11]and Hussein, et al[12], experimentally examined the friction factor and forced convection heat transfer enhancement of a water based nanofluid with various nanoparticles in the automotive cooling system. In general, the results showed that the use of nanofluids increased the friction factor and forced convective heat transfer coefficient, so that the percentage increase in heat transfer coefficient was more than the percentage increase of the friction factor.

In most of the existing equipment in various industries, a magnetic field is created due to the electric field. Thus the flow of electrically conducting fluid through a channel or a duct is exposed to a transverse magnetic field. The results of the research conducted have shown that the fluid flow subjected to a magnetic field, experience a Lorentz force. Lorentz force directly affects the flow field and consequently the heat transfer is also affected. Therefore, understanding of the flow and thermal behaviors of the channels that are cooled by electrically conducting fluids and are exposed to a magnetic field has long been of interest to researchers. Siegel[13]was among the first researchers who have studied the hydromagnetic flows. He studied convective heat transfer for the fully developed and laminar flow of an incompressible and electrically conducting fluid in a parallel plate channel submitted to a constant and uniform heat flux at the walls and exposed to a transverse magnetic field. The results showed that the flow field and the heat transfer in the channel were affected by the magnetic field. Alpher[14]continued and extended the earlier study done by Siegel[13]. In particular the earlier analysis of Siegel involving non-conducting plates were corrected and extended to plates of finite conductivity. Back[15]analytically studied the uniform laminar flow of an electrically conducting fluid in a constant cross-section, parallel-plate channel with isothermal, electrically nonconducting walls. In this study, the effect of the Joule heating parameter was also considered. The results showed that the thermal entrance lengths were proportional to Reynolds and Prandtl numbers, similar to the case of no applied magnetic field. Additionally, these lengths decreased with an increase in Joule heating parameter. Lahjomri, et al[16], analytically investigated the thermal developing laminar Hartmann flow through a parallel plate channel, including viscous dissipation, Joule heating and axial conduction with a step change in wall temperature. The results showed that in the absence of viscous dissipation and Joule heating, the Hartman effect led to a reduction of the bulk temperature. This study also showed that viscous dissipation and Joule heating played a significantly different role in the heat transfer, depending on the electrical condition of the walls. In another study, Lahjomri, et al[17], reiterated his earlier work under a constant heat flux boundary condition. This time, they showed that the heat transfer increased with the increasing Hartmann number until finally a saturated state was achieved.

With the arrival of nanofluids to the technology arena, the interest to examine the hydro-magnetic flow of nanofluids has greatly increased. Aminossadati, et al[18], numerically examined the laminar forced convection of a water–Al2O3nanofluid flowing through a partially heated microchannel. They indicated that for any value of the Reynolds number, velocity and temperature along the centerline of the microchannel decreased as the Hartmann number increased. Their results also showed that the Nusselt number increased as the Reynolds and Hartman numbers increased. Mahian, et al[19], analytically investigated the effects of using TiO2/water nanofluid on the entropy generation in an isoflux vertical annulus under MHD flow effects. In this study the flow was assumed as laminar, steady and fully developed inside the annulus. The results showed that using TiO2/water nanofluid reduced the entropy generation in the annulus while an increase in the Hartmann number increased the entropy generation number. SyamSundar, et al[20], experimentally examined the forced convection heat transfer and friction factor in a tube with Fe3O4magnetic nanofluid. In this study, the heat transfer coefficient increased by 30.96% and friction factor by 10.01% at 0.6% volume concentration compared to flow of water at similar operating conditions. Ghofrani, et al[21], established an experimental investigation on laminar forced convection heat transfer of ferrofluids inside a circular copper tube under an alternating magnetic field. They investigated the effects of magnetic field, volume concentration and Reynolds number on the convective heat transfer coefficient. They found that increasing the frequency of the alternating magnetic field and the solid volume fraction, led to better heat transfer enhancement. Malvandi, et al[22], presented a theoretical study on the laminar flow and forced convective heat transfer of water/alumina nanofluid inside a parallel plate channel in the presence of a uniform magnetic field. They applied a modified two component model for water/alumina nanofluid and looked at the migration of nanoparticles. The results indicated that nanoparticles moved from the heated walls toward the core region of the channel and constructed a non-uniform nanoparticles distribution.

It is worth mentioning that previous studies have solely investigated heat transfer in a single channel. However, in many engineering applications, such as heat exchangers, hot and cold fluids flow through a pair of adjacent channels, and forced convective heat transfer takes place between them. In fact, this system can be a simple model of a heat exchanger, which is exposed to a uniform magnetic field to increase the rate of heat transfer. The main aim of the present work is a numerical investigation of heat transfer performance of a Cu-water nanofluid in a pair of horizontal channels that is under the influence of a transverse magnetic field. It is assumed that the flows are separated by a thin plat (membrane) which its mass is negligible.

2 Problem Description

Fig. 1 shows the schematic diagram of a two-dimensional horizontal channel wherein hot and cold flows are separated by a membrane. Dimensionless height and length areandrespectively.

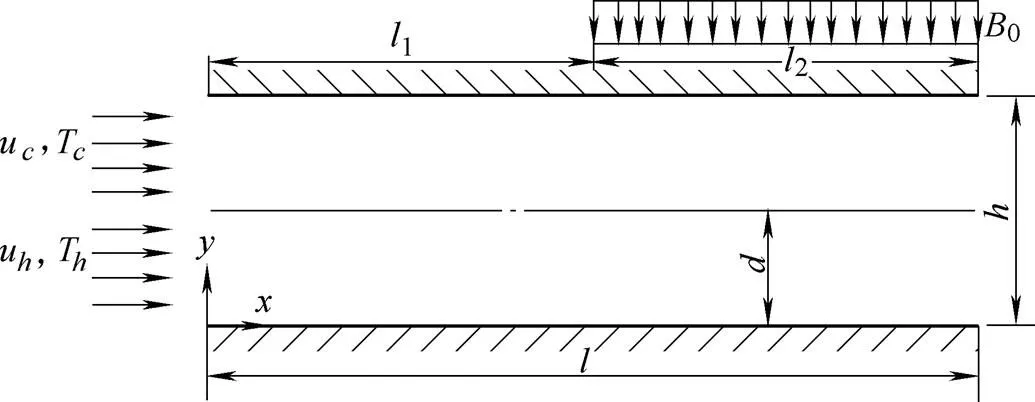
Fig. 1. A schematic diagram of the physical model

Both upper and lower walls of the channel are thermally insulated. The first part of the channel which is not influenced by magnetic field (Non-Magnetic part, i.e., NMP here after) has a dimensionless length ofand the second part influenced by magnetic field (magnetic part, i.e., MP from now on) has the same dimensionless length ofHot flow with velocityand temperatureand cold flow with velocityand temperatureenter lower and upper channels respectively. Both hot and cold nanofluid flows contain water and Cu nanoparticles and are assumed to be laminar, Newtonian and incompressible. Constant thermophysical properties are considered for the nanofluid, except for the density variation in the buoyancy forces that is determined by the Boussinesq approximation.

The thermophysical properties of pure water (base fluid) and the Cu-nanoparticles, at a fixed temperature of 25℃, are presented in Table 1[23]. The Prandtl number of water is assumed to be

Table 1. Thermophysical properties of water and Cu at 25℃

3 Mathematical Formulation

The non-dimensional governing equations of continuity, momentum, and energy for hot and cold flows can be written as follow (is for hot flow andis for cold flow:

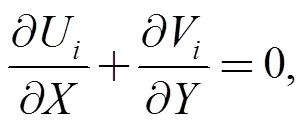
(2)

(3)

(5)

The Reynolds, Hartman and Prandtl numbers are:

The effective density, heat capacitance and the thermal diffusivity coefficient of the nanofluid are defined based on the properties of water and Cu[23]:

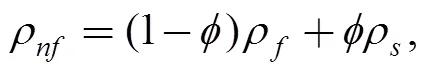
(8)

(9)

The electrical conductivity of nanofluid was presented by Maxwell[24]as below:

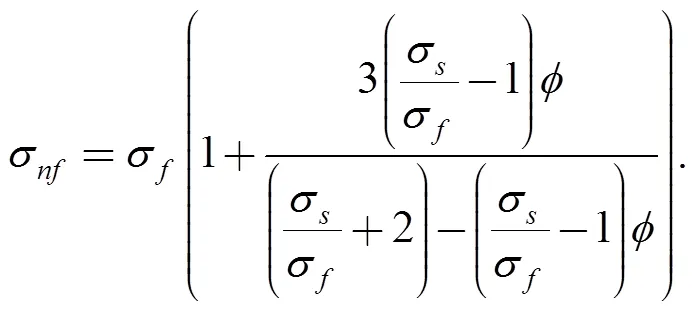
The effective dynamic viscosity of the nanofluid can be modeled by Brinkman[25]:

(11)

The thermal conductivity of the nanofluidkwas determined by Patel, et al[26]. For the two-component entity of spherical-particle suspension, the model gives:

where

(13)

(15)

In the above-mentioned equations,is the Boltzmann constantandis an experimental constant (=36 000) which was suggested by Patel, et al[26]. The molecular diameter of the solid nanoparticles is100 nm and the molecular diameter of the base fluid is2°A.

The non-dimensional boundary conditions used to solve Eqs. (1)–(4) are as follows:

Since the membrane is thin and its mass is negligible, the thermal boundary conditions on it are as follows:

(17)

4 Numerical Approach

The non-dimensional governing equations for hot and cold flows (Eqs. (1)–(4)) with the boundary conditions given in Eqs. (16) and (17) are solved simultaneously by the control volume formulation using Patankar’s SIMPLE algorithm[27].

The convection-diffusion terms are discretized by a power-law scheme, and the system is numerically modeled in FORTRAN. A regular rectangular domain with a uniform grid is used. The convergence criteria are to reduce the maximum mass residual of the grid control volume below 108.

After solving both the hot and the cold governing equations forandother useful quantities such as the Nusselt number can be determined. The local Nusselt number () at the membrane can be expressed as:

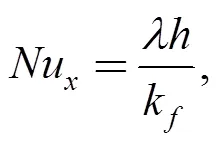
where 𝜆 is the convection heat transfer coefficient and is calculated as follows:

(19)

Thus the local Nusselt number by using the dimensionless parameters given in Eq. (5) is as follows:

(21)

Finally, the average Nusselt number () is determined by integratingalong the membrane separator:

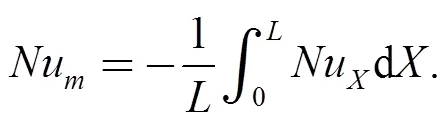
5 Grid Independency and Code Validation

Table 2 indicates the solution grid independence for two different Hartmann numbers

Table 2. Grid independency study at Re=100 f=0.03, D=1/2, VC1=1

The average Nusselt number and the dimensionless bulk mean temperature of hot and cold flows at channels’ outlet, i.e., (1)outand (2)outare presented at different grid points when=0.03,1=1, and=1/2. The obtained results from Table 2 illustrates that the grid size of 81´400 satisfies grid independency.

Fig. 2(a) compares the isotherms of this work with those of Santra, et al[8]to validate our code. Moreover, the variation of temperature along the centerline of the channel for=100 and=0.02 of Al2O3-Water Nanofluid is compared with that of Aminossadati, et al[18]in Fig. 2(b).

Furthermore, in Fig. 2(c) the fully developed velocity profiles at three values of Hartman number contrasted with Back’s findings[15]presented by Eq. (23). Good agreements are seen in all Figs. 2(a), 2(b) and 2(c).

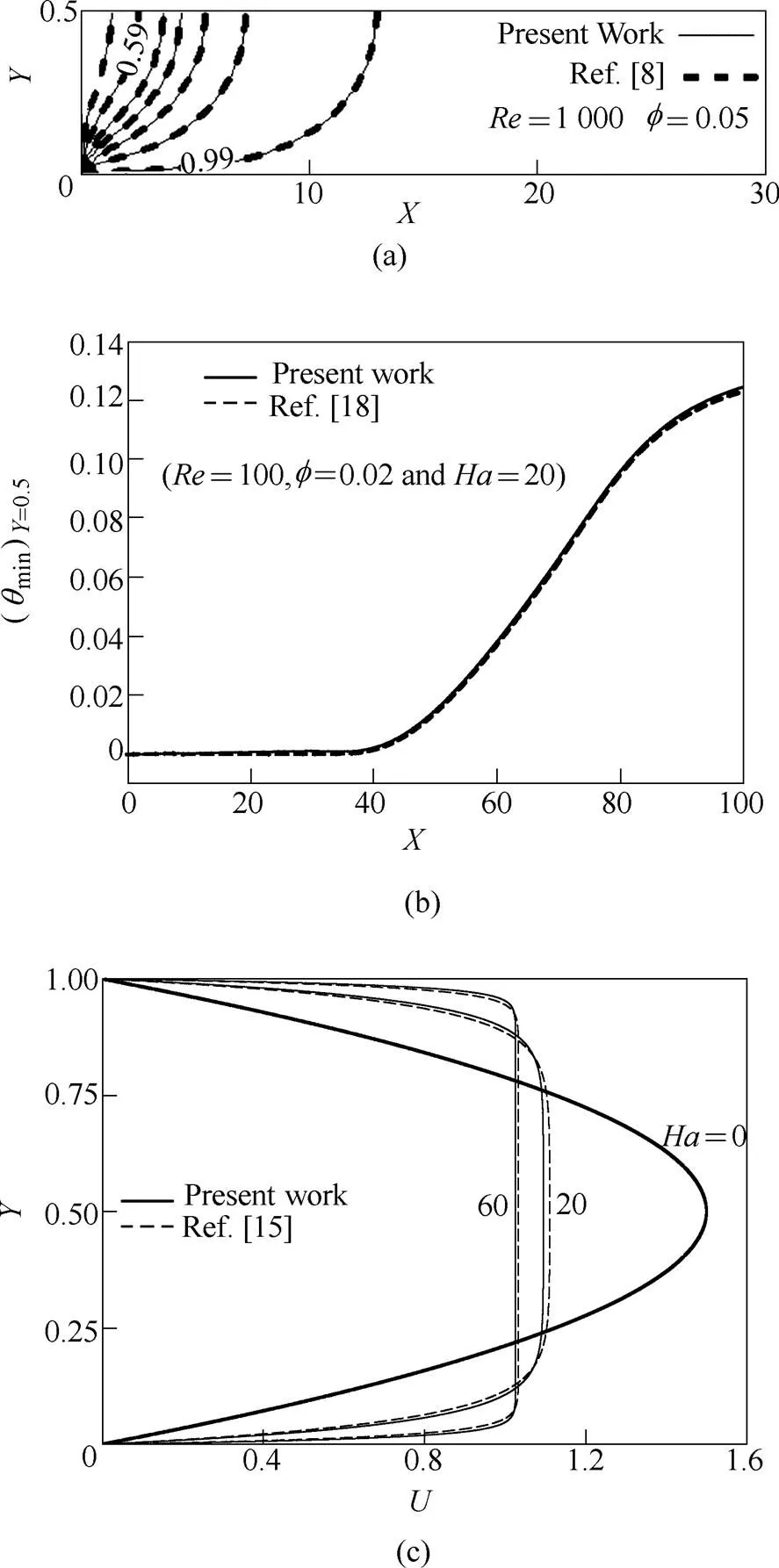
Fig.2. Validation code against: (a) Isotherms inRef. [8], (b) Variation of temperature along the centerline of the channel inRef. [18], and (c) Analytical velocity profile modeled inRef. [15]

6 Results

The effects of the Reynolds number (10≤≤500), the Hartman number (0≤≤60) and the solid volume fraction (0≤≤0.05) on the thermal performance of the channel are studied and are presented in the following sections forand

6.1 Effects of Reynolds and Hartman numbers

In this section, the effects ofandon heat transfer, isotherms and streamlines are studied when=0.03. Streamlines and isotherms are shown in Fig. 3 at different values offor=0 and 40. In all values of, streamlines match together at NMP, whereas at=40 both the hot and the cold flows affected by magnetic field at MP where streamlines expand due to Lorentz force.

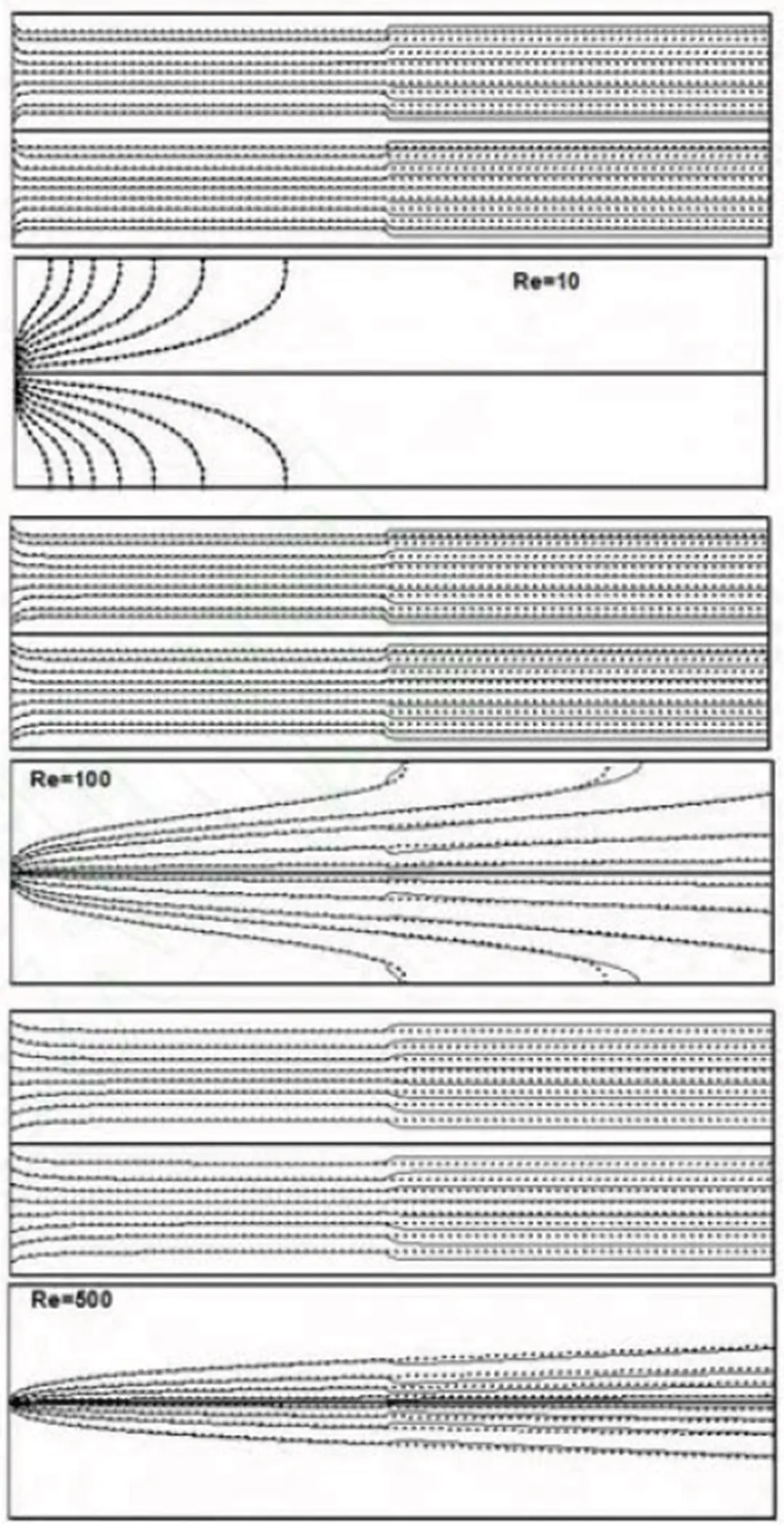
Fig. 3. Streamlines (top) and isotherms (bottom) for Cu-water nanofluid (f=0.03) for different Re at Ha=40 and Ha=0

Isotherms are not affected by the magnetic field at=10, and they are the same for=0 and 40. This is due to the small amounts of hot and cold flows’ velocities at=10, so both flows reach a balanced temperature very soon. Other findings show that heat transfer occurs throughout the channel length at=100 and 500. Thus the temperature patterns do penetrate into the exit section and at=40, isotherms are influenced by magnetic field at MP. The comparison between the isotherms of the nanofluid near the membrane shows that the heat transfer increases as theincreases.

Fig. 4 presents the variations of dimensionless velocities along the centerline of hot or cold flows at=10 100 and 500. It is observed that both flows have the same velocity variations along the flow centerline in all values ofbecause of their similar geometric and hydrodynamic properties. In this figure, it can be seen that at=10 centerline velocity stabilizes much sooner in comparison with other values of. In addition, the length of hydrodynamic entrance increases as theincreases. However,maxdecreases due to the magnetic field effect by entering hot and cold flows to the MP. The gradient of this decrease depends on.

Fig. 4. Variation of horizontal velocity along the centerlineof the channel for various Reynolds numbers atHa=40, f=0.03

In Fig. 5,maxvariations are presented at four different values of Hartman number (=0, 20, 40 and 60) and=100. In the absence of magnetic field (=0), the maximum of horizontal flow velocity is constant at fully developed conditions, due to Lorentz force effect, however,maxdecreases at0. The highest decrease ofmaxachieves for the largest amount of(see Eq.(2)).

Fig. 6 shows the velocity profiles at four different cross sections of channel; namely=7.5, 15, 22.5 and 30,for hot and cold nanofluid flows at=40 and=100. According to this figure, the velocity profile at=7.5 is parabolic and fully developed. The magnetic field starts at=15 where the shape of velocity profile begins to change. In two sections of=22.5 and 30, magnetic field yields a similar flat velocity profile for both sections.

Reynolds and Hartman numbers’ effects onNuare shown in Figs. 7(a) and 7(b). Highercorresponds tohigherNu. Regardless of the values ofand, the maximum amount ofNuis obtained at the channel inlet due to the highest temperature gradient between hot and cold flows. After heat exchange between two nanofluid flows along the membrane length,Nustarts to decrease. For=10, two flows reach a thermal equilibrium immediately. Thus, in this case, magnetic field has no significant effect on isotherms’ variations andNu. For=100and 500, an increasing jump can be observed inNudiagram at the entrance of MP. This happens because in the existence of magnetic field, the velocity of two flows near the walls and membrane increases.

节理等密图的自动绘制………………………………………………………………………………………………李玉华（1.21）

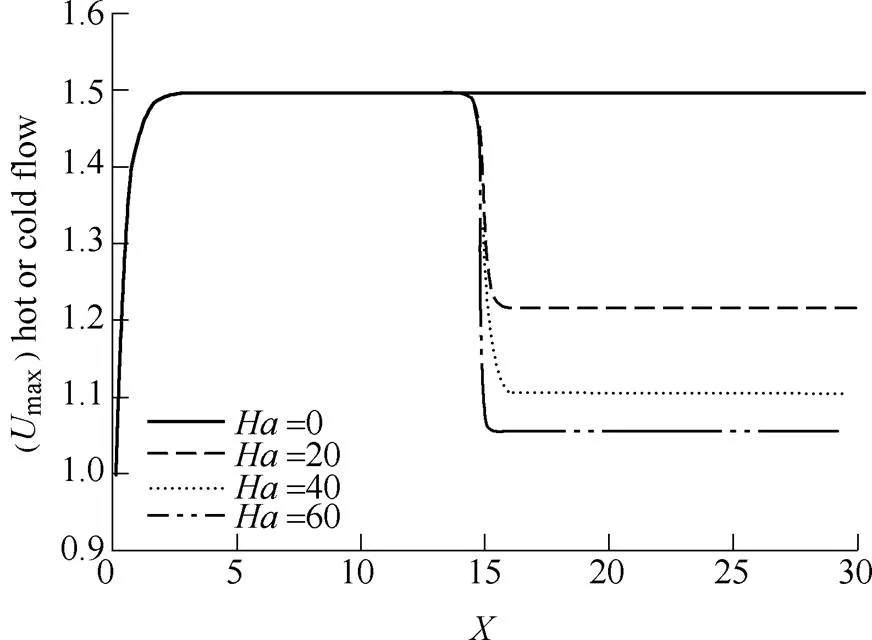
Fig. 5. Variation of horizontal velocity along the centerline of the channel for various Hartman numbers at=100,=0.03

Fig. 6. Horizontal velocity profiles across various sections of channel at=0.03,=100,=40

The effects ofon Nusselt number can be better understood by studying values presented in Table 3. As mentioned before, the increase inleads to the increase inNuat higher values of. After running the computer code for different values of the Reynolds and Hartmann numbers, the following correlation was found between the average Nusselt, Reynolds and Hartmann numbers when the solid volume fraction=0.03.

where

(25)

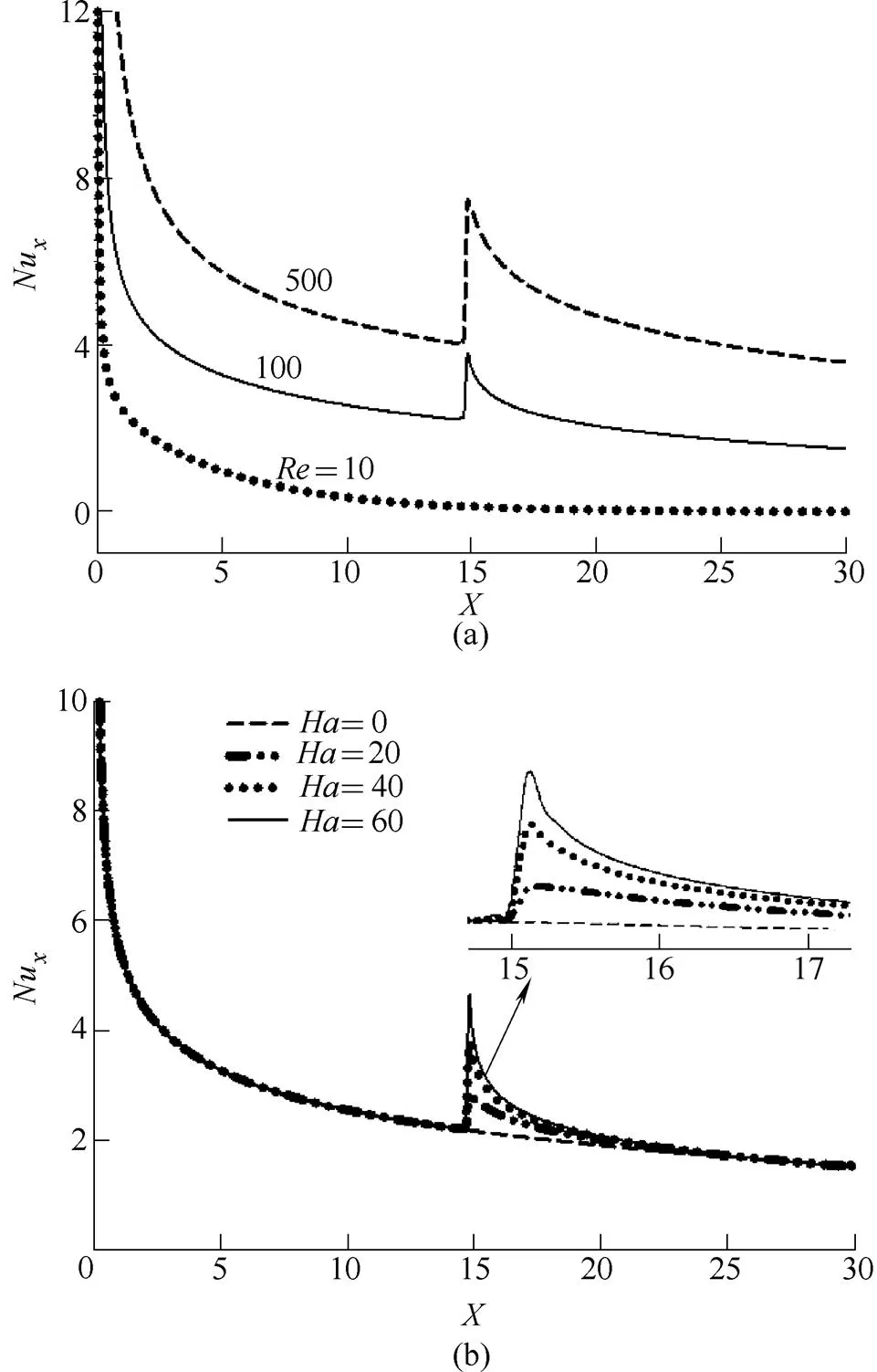
Fig. 7. Variation of local Nusselt number along the channel length at=0.03, and at (a) various Reynolds numbers at=40, (b) various Hartman number at=100

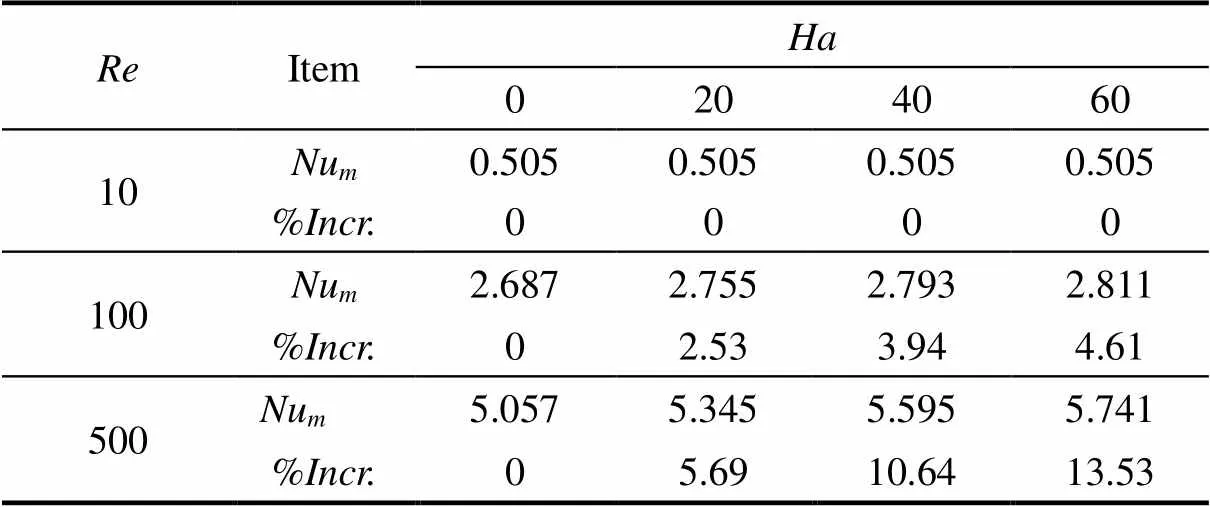
Table 3. Effects of Ha on the Num and its relative increase percentage (%Incr.) at various Reand f=0.03

Note: %means relative increase percentage,

6.2 Effect of solid volume fraction

Figs. 8(a) and 8(b) show that the dimensionless bulk mean temperatures of the hot and the cold flows start to decrease and increase respectively as soon as they enter the channel. The rate of temperature change is higher at low values of, so that for=10, the dimensionless bulk mean temperatures of the two flows become equal before reaching the exit section for both the nanofluid and pure water while for=100 and 500 these temperatures are substantially different from each other. For all values of, the changes in dimensionless bulk mean temperature are more rapid for nanofluid flow than that of pure water. Figs. 8(a) and 8(b) also show that in all values of, the hot and the cold flows have the same hydrodynamic conditions, and variations of flows’ temperature along the channel are symmetrical.

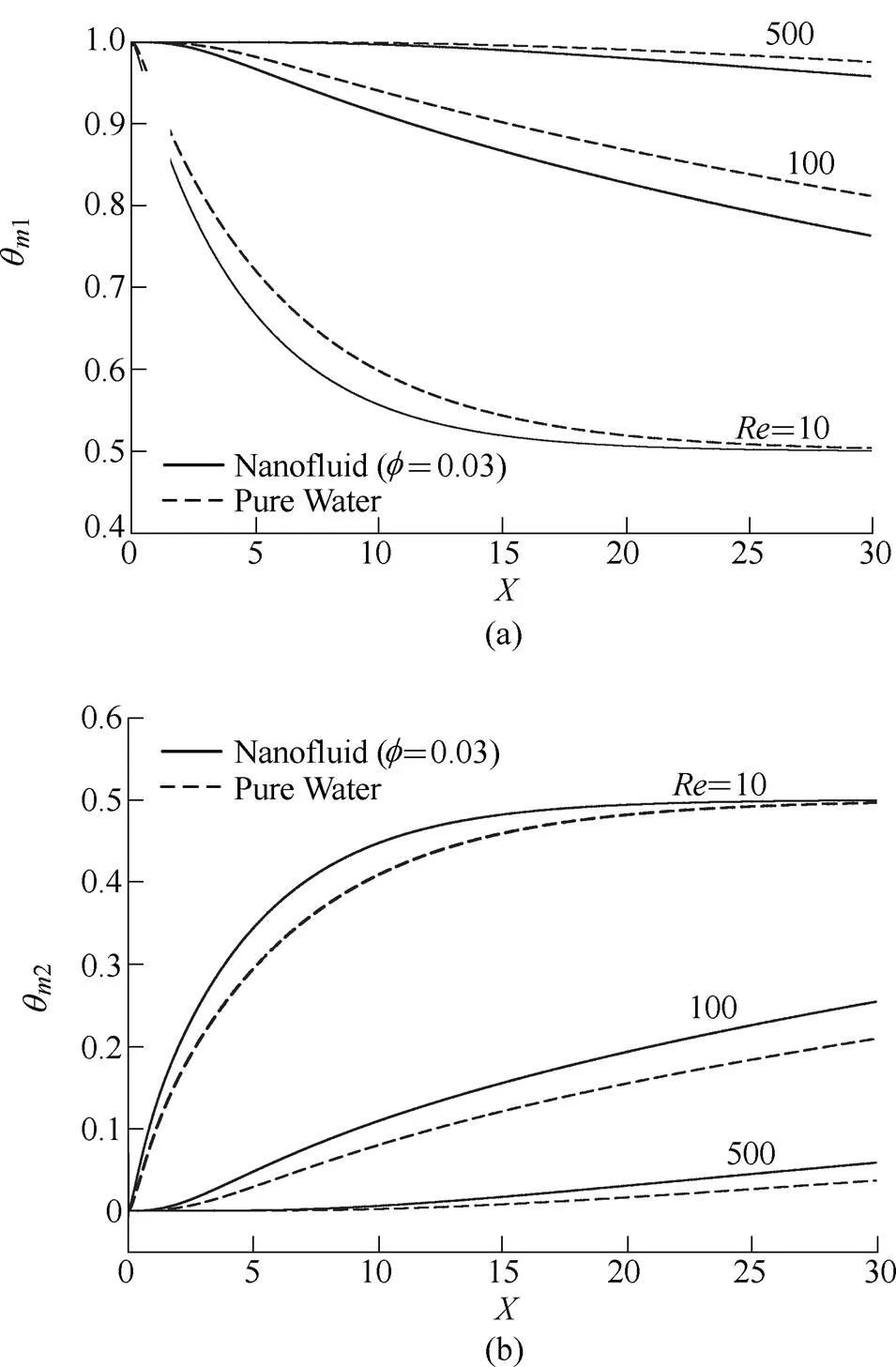
Fig. 8. Variation ofdimensionless balk mean temperature along the channel length for nanofluid (=0.03), and pure water at various Reynolds numbers and=40, for (a) hot flow and (b) cold flow

Nuat different values of copper nanoparticles volume fraction (0≤≤0.05) for=0 and 40 is presented in Table 4 at different values of. In all cases, higher values ofNucan be achieved at higher amounts of. As a result, it can be said that the effects ofandon increasingNuare more significant for higher values of. For example, at=500 and=40, an increase of 3% in the volume fraction of copper nanoparticles results in approximately 18.84% increase in theNu, whereas this values is 1.0% for=10 and=40.

After running the computer code for different values of the Reynolds numbers and solid volume fractions, the following correlation was found between the average Nusselt and Reynolds numbers and solid volume fractions when the Hatrmann number is=0 and 50≤≤500.

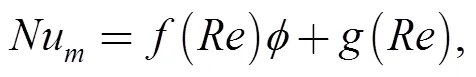
where

(27)

Table 4. Effects of f on the Num and its relative increase percentage for different values of Re and Ha

Note: %means relative increase percentage,

7 Conclusions

The flows were becoming fully developed later at higher values of the Reynolds number. Streamliners were expanded at MP due to applying the magnetic field. The Hartman number had no effect on heat transfer rate at=10 because two flows were reached an equal temperature immediately. This is while at higher values of Reynolds number, the average Nusselt number increased as the Hartman number increased. Moreover, a more noticeable increase in the Nusselt number with solid volume fraction was evident at higher values of Reynolds number.

Nomenclature

B0—Magnetic field strength, c—Experimental constant, Eq. (12), Cp—Specific heat, J • kg–1• K–1, d—Distance between channel’s bottom wall and membrane, m, D—Dimensionless distance between channel’s bottom wall and membrane, D=dh, h—Channel height, m H—Dimensionless channel height, H=h/h=1, Ha—Hartman number, k—Thermal conductivity, W • m–1• K–1, l—Length of channel, m, L—Dimensionless length of channel, L1—Dimensionless length of first region, without of magnetic field, L2—Dimensionless length of second region, with of magnetic field MP—Part of channel’s wall that is influenced by magnetic field, (magnetic part) NMP—Part of channel’s wall that is not influenced by magnetic field, (non-magnetic part), Nux—Local Nusselt number on the membrane, Num—Average Nusselt number along the membrane, p1—Hot flow pressure, Pa, p2—Cold flow pressure, Pa, —Modified pressure, P1—Dimensionless pressure for hot flow, P2—Dimensionless pressure for cold flow, Pe—Peclet number, Pe= Pr—Prandtl number, Pr= Re—Reynolds number, Re= T1, T2—Temperature of hot and cold flows respectively, K, Tc—Inlet temperature of cold flow, K, Th—Inlet temperature of hot flow, K, us—Brownian motion velocity, m/s, u, v—Velocity components in x, y directions, m/s, U1, V1—Dimensionless velocity of hot flow, U2, V2—Dimensionless velocity of cold flow, VC1—Velocity coefficient, x, y—Cartesian coordinates, , X, Y—Dimensionless coordinates, X=x/h, Y=y/h, a—Thermal diffusivity (k/rCp), m2/s, f—Solid volume fraction, kb—Boltzman constant, J/K, q1—Dimensionless temperature of hot flow, q2—Dimensionless temperature of cold flow, qm1—Dimensionless balk mean temperature of hot flow, qm3—Dimensionless balk mean temperature of cold flow, l—Heat transfer coefficient, W • m–2• K–1, m—Dynamic viscosity, N • s • m-2, —Kinematic viscosity (m/r), m2/s, r—Density, kg • m–3, s—Electrical conductivity, mS/cm. Subscripts C, 2—Cold, h, 1—Hot, eff—Effective, f—Pure fluid, nf—Nanofluid, out—Channel’s outlet, s—Nanoparticle.

[1] Choi, SUS. Enhancing thermal conductivity of fluids with nanoparticles[J], 1995, 66: 99–105.

[2] Eastman J A, Choi SUS, Li S, et al. Anomalously increased effective thermal conductivities of ethylene glycol-based nanofluids containing copper nanoparticles[J]., 2001, 78(6): 718–720.

[3] Zhou D W. Heat transfer enhancement of copper nanofluid with acoustic cavitation[J]., 2004, 47: 3109–3117.

[4] Moghadassi A R, MasoudHosseini S, Henneke D E. Effect of CuO nanoparticles in enhancing the thermal conductivities of mono ethylene glycol and paraffin fluids[J].2010, 49: 1900–1904.

[5] Sahooli M, Sabbaghi S, Investigation of thermal properties of CuO nanoparticles on the ethylene glycol–water mixture[J]., 2013, 93: 254–257.

[6] Izadi M, Behzadmehr A, Jalali-Vahida D. Numerical study of developing laminar forced convection of a nanofluid in an annulus[J]., 2009, 48(4): 2119–2129.

[7] Bianco V, Chiacchio F, Manca O, et al. Numerical investigation of nanofluids forced convection in circular tubes[J]., 2009, 29: 3632–3642.

[8] Santra A K, Sen S, Chakraborty N. Study of heat transfer due to laminarflow of copper–water nanofluid through two isothermally heated parallel plates[J]., 2009, 48: 391–400.

[9] Manca O, Nardini S, Ricci D. A numerical study of nanofluid forced convection in ribbed channels[J].,2012, 37: 280–292.

[10] Saha G, Paul CM. Numerical analysis of the heat transfer behaviour of water based Al2O3and TiO2nanofluids in a circular pipe under the turbulent flow condition[J]., 2014, 56: 96–108.

[11] Peyghambarzadeh S M, Hashemabadi S H, SeifiJamnani M, et al. Improving the cooling performance of automobile radiator with Al2O3/water nanofluid[J].2011, 31: 1833–1838.

[12] Hussein A M, Bakar R A, Kadirgama K. Study of forced convection nanofluid heat transfer in the automotive cooling system[J]., 2014, 2: 50–61.

[13] Siegel R. Effect of magnetic field on forced convection heat transfer in a parallel plate channel[J]., 1958, 25: 415–420.

[14] Alpher R A. Heat transfer in magneto hydrodynamic flow between parallel plates[J].,1961, 3(2): 108–112.

[15] Back L H. Laminar heat transfer in electrically conducting fluids flowing in parallel plate channels[J]., 1968, 11: 1621–1636.

[16] Lahjomri J, Oubarra A, Alemany A. Heat transfer by laminar Hartmann flow in thermal entrance region with a step change in wall temperatures: the Graetz problem extended[J]., 2002, 45(5): 1127–1148.

[17] Lahjomri J, Zniber K, Oubarra A, et al. Heat transfer by laminar Hartmann’s flow in thermal entrance region with uniform wall heat flux: the Graetz problem extended[J].,2003, 44(1): 11–34.

[18] Aminossadati S M, Raisi A, Ghasemi B. Effects of magnetic field on nanofluid forced convection in a partially heated microchannel., 2011, 46: 1373–1382.

[19] Mahian O, Pop I, Sahin Z A, et al. Irreversibility analysis of a vertical annulus using TiO2/water nanofluid with MHD flow effects[J]., 2013, 64: 671–679.

[20] SyamSundar L, Naik M T, Sharma K V, et al. Experimental investigation of forced convection heat transfer and friction factor in a tube with Fe3O4magnetic nanofluid[J]., 2011, 37: 65–71.

[21] Ghofrani A, Dibaei M H, Hakim-Sima A, et al. Experimental investigation on laminar forced convection heat transfer of ferro-fluids under an alternating magnetic field[J]., 2013, 49: 193–200.

[22] Malvandi A, Ganji D D. Magnetic field effect on nanoparticles migration and heat transfer of water/alumina nanofluid in a channel [J].,2014, 362: 172–179.

[23] Raisi A, Ghasemi B, Aminossadati S M. A numerical study on the forced convection of laminar nanofluid in a microchannel with both slip and no-slip conditions[J].,, 2011, 59(2): 114–129.

[24] Sheikholeslami M, Soleimani S, Gorji-Bandpy M, et al. Natural Convection of nanofluids in an enclosure between a circular and a sinusoidal cylinder in the presence of magnetic field[J]., 2012, 39: 1435–1443.

[25] Brinkman H C. The viscosity of concentrated suspensions and solution[J]., 1952, 20: 571–581.

[26] Patel H E, Sundararajan T, Pradeep T, et al. A micro-convection model for thermal conductivity of nanofluids[J]., 2005, 65(5): 863–869.

[27] Patankar S V.[M]. New York: Hemisphere Publishing Corporation-Taylor and Francis Group, 1980.

Biographical notes

Afrasiab Raisi was born in Iran and currently is an associate professor atHe received his B. Eng. Degree in Mechanical Engineering fromin 1992, and the M.Sc. and Ph.D. degrees in Mechanical Engineering from, in 1995 and 2001, respectively. In 2001, he joined theas an assistant Professor, became an associate professor in 2015. His current research interests include forced and natural convection heat transfer, convective heat transfer in nanofluids and non-Newtonian fluids, melting and solidification and conduction microscale heat transfer.

Tel: +98-3832324435;

E-mail: afraisi@gmail.com; raisi@eng.sku.ac.ir

Ahmad Qanbary was born in Iran in 1980 and currently is an engineer atHe received his M.Sc. degree in Mechanical Engineering (CFD branch) fromin 2013.

E-mail: ahmadqanbary@yahoo.com

Received August 17, 2015; revised May 30, 2016; accepted June 15, 2016

© Chinese Mechanical Engineering Society and Springer-Verlag Berlin Heidelberg 2016

10.3901/CJME.2016.0615.072, available online at www.springerlink.com; www.cjmenet.com

E-mail: raisi@eng.sku.ac.ir